基于平衡和非平衡權重算法的柴油機有機朗肯循環多目標優化

黨玉榮,莫春蘭,方穎聰,史科銳,張子楊,李作順

(廣西大學機械工程學院,廣西 南寧 530004)

目前,柴油發動機燃料產生的能量只有40%左右被轉化為有用功[1],大部分能量以熱損失的形式被釋放到環境中(如廢氣、夾套冷卻水和潤滑油等)[2]。其中柴油機廢氣的能量損失最大[3],所以高效回收廢氣余熱對提高柴油機效率,實現節能減排具有重要的意義。有機朗肯循環(ORC)是進行余熱回收、提高系統效率的有效方法[4]。

綜上所述,目前對基于柴油機余熱回收的非共沸混合工質ORC系統的多目標優化分析的研究較少,并且大部分研究對ORC系統的多目標優化都是基于平衡權重優化,對于非平衡權重優化缺少討論。因此,本研究對非共沸混合工質ORC系統進行了非平衡權重和平衡權重的多目標優化分析,與傳統的優化算法不同,本研究引入RPD-NSGA-Ⅱ(reference point dominance-based NSGA-Ⅱ)[16]算法進行多目標優化,該算法基于NSGA-Ⅱ進行改進,具有更好的解的多樣性、更快的收斂速度以及更強的多目標優化能力,可處理ORC系統性能的復雜變化,最后通過TOPSIS(優劣解距離法)[7]進行綜合分析,可為實際工程提供理論依據。

1 有機朗肯循環的模型分析

1.1 ORC系統描述

利用基于非共沸混合工質的有機朗肯循環對柴油發動機廢氣余熱進行回收。以某直列6缸渦輪增壓的柴油發動機為例[6],表1列出了發動機的主要參數。考慮發動機的廢氣溫度較高,并且Ge等[17]研究表明非共沸混合工質(苯/甲苯)的輸出功率高于相應的純工質,所以系統選擇了臨界溫度較高的苯和甲苯作為ORC的候選工質。工質的基本物性如表2所示[5,17]。圖1示出了ORC系統的結構和溫熵變化,整個熱力過程為亞臨界有機朗肯循環。首先,柴油發動機的廢氣在蒸發器與ORC的工質進行熱交換,將工質加熱成飽和蒸氣(過程1—3),之后飽和蒸氣在汽輪機膨脹做功(過程3—4),做功后的乏汽被冷凝器冷卻成飽和液態(過程4—6),最后飽和液被泵加壓后再次送到蒸發器(過程6—1)完成ORC循環。值得注意的是,由圖1b可知基于非共沸混合工質的ORC系統的工質和和熱源的匹配度更高。

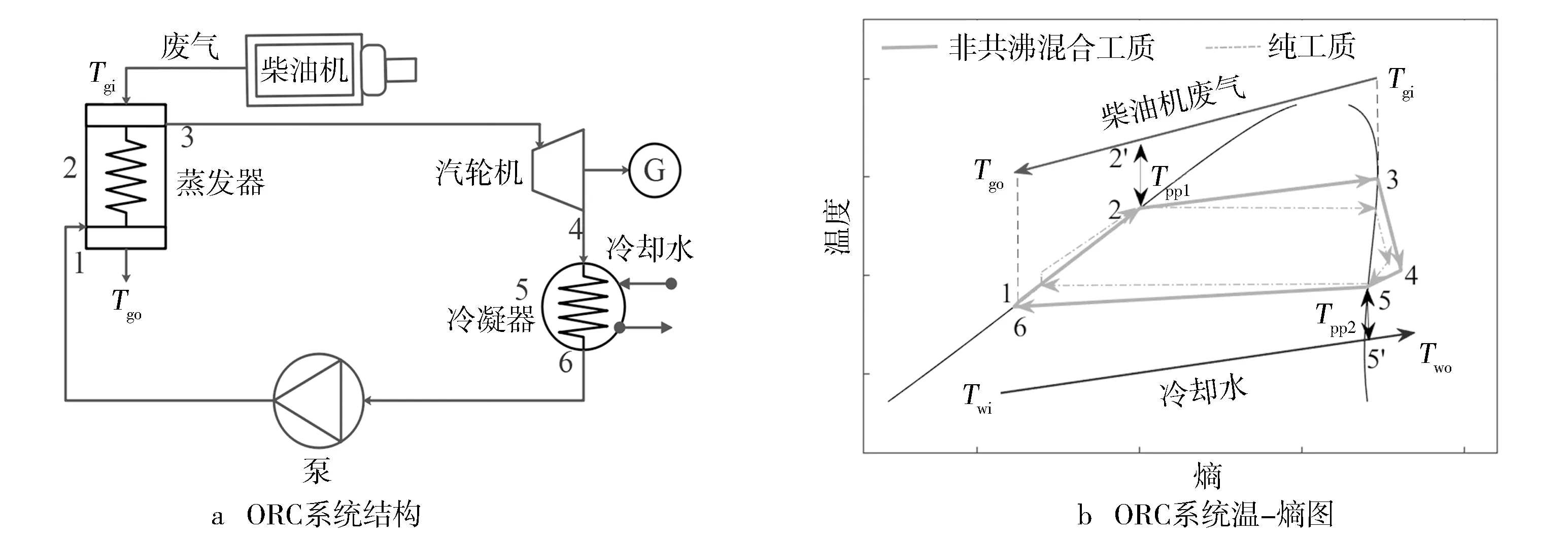
圖1 ORC系統的結構和溫-熵圖

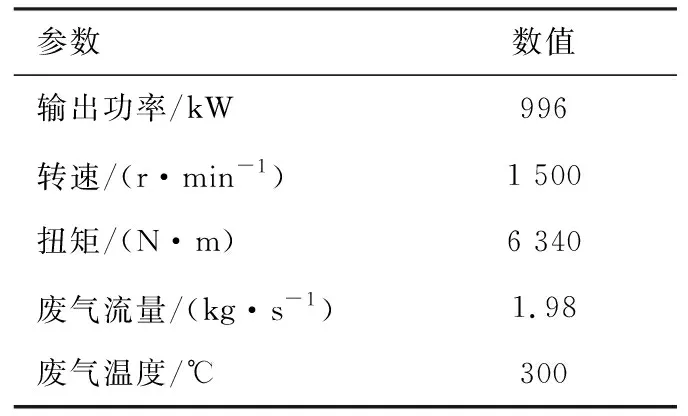
表1 柴油發動機的主要參數[6]

表2 工質的基本物性[5,17]

1.2 有機朗肯循環的熱力學模型

在MATLAB中建立了系統的熱力學模型,利用REFPROP可以獲得工質的熱力學性質。為了簡化ORC的熱力學模型,提出了以下幾個假設和條件:

1) ORC系統始終處于穩態運行狀態,并忽略循環中的能量、摩擦和壓力損失等;

2) 泵和渦輪的等熵效率分別為ηp=0.8和ηt=0.88;

3) 假設氣液換熱器夾點溫度(Tpp,gl)和液液換熱器夾點溫度(Tpp,ll)分別為30 ℃和5 ℃;

4) 假設大氣溫度(T0)和壓力(p0)分別為25 ℃和0.1 MPa;

5) 為避免酸腐蝕,蒸發器廢氣出口溫度應不小于105 ℃;

6) 假設冷卻水進口溫度(Twi)為25 ℃,冷卻水出口溫度(Two)為35 ℃;

假設Tpp1=Tpp,gl,則ORC的質量流量(mORC)和蒸發器廢氣出口溫度(Tgo)分別為

(1)

(2)

T2′′=T2+Tpp1。

(3)

式中:T2為蒸發溫度;Cg為廢氣的比熱容;h為流體的焓值。

假設Tpp2=Tpp,ll,則冷卻水的質量流量(mw)為

(4)

(5)

Tpp2=T5-T5′′。

(6)

式中:Cw為冷卻水的比熱容。

1.2.1 能量模型

根據熱力學第一定律,各設備的能量平衡方程列于表3。

表3 ORC系統組件的能量方程

系統輸出功率(Wnet):

Wnet=Wt-Wp;

(7)

系統熱效率(ηth):

(8)

柴油機廢氣能量(Qg):

Qg=Cg×mg(Tgi-T0);

(9)

柴油機廢氣能量回收率(ηg):

(10)

式中:Wt為汽輪機功率;Wp為工質泵功率;Qeva為蒸發器換熱量。

表4 ORC系統設備的損方程

Izon=Ieva+Icon+It+Ip。

(11)

1.3 有機朗肯循環模型驗證

為了保證仿真模型的準確性,采用了文獻[18]中的ORC模型來確認計算的準確性。建立相同的邊界條件:T3=88.86 ℃,T6=27.1 ℃,P2=PL=0.708 MPa,mORC=0.82 kg/s。如表5所示,模型與文獻之間存在良好的一致性,最大誤差為0.72%(小于5%),所以模型計算的數據是可靠的。

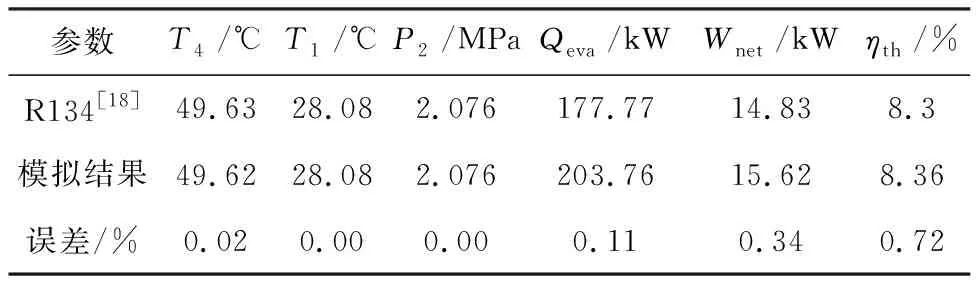
表5 ORC模型的對比結果

1.4 ORC系統的熱力學性能分析

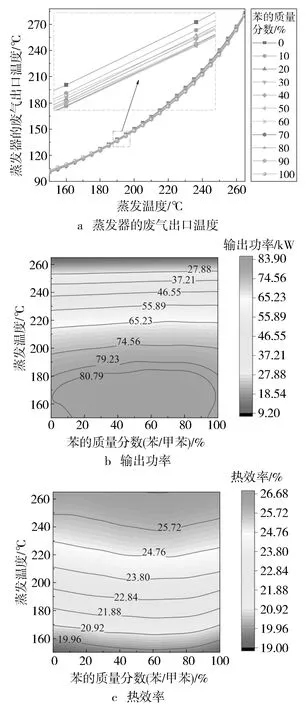
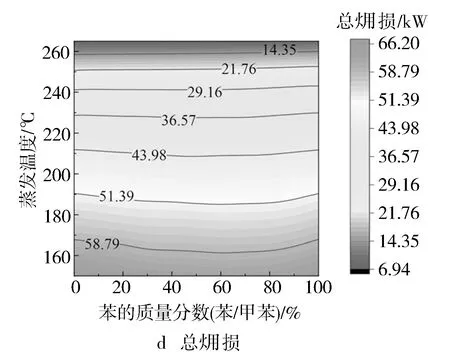
圖2 ORC系統的熱力學性能分析

2 基于熱力學性能的多目標優化

2.1 RPD-NSGA-Ⅱ算法設計

RPD-NSGA-Ⅱ[16]基于傳統NSGA-Ⅱ進行改進,在保持帕累托排序的同時強調了收斂性和多樣性。為了驗證RPD-NSGA-Ⅱ算法的優越性,通過引入多目標優化評價指標IGD(反轉世代距離)可以評價算法的收斂性和多樣性[19],而IGD值越小對應的算法性能越優異。

2.2 目標函數和決策變量

表6 決策變量的變化范圍

max(Wnet)=f1(T2,mf),

(12)

max(ηth)=f2(T2,mf),

(13)

min(Izon)=f3(T2,mf)。

(14)

2.3 多目標優化決策

經過優化算法得到的Pareto解集都是目標的最優解,需要根據不同目標函數的權重進行歸一化后選出最滿意的解。而TOPSIS可以利用數據的差異來進行決策和分析數據之間的差距,并確定最佳的運行參數[7]。具體計算如下:

優化解集與理想點之間的空間距離可計算為

(15)

從優化解集到非理想點的距離被定義為

(16)

評價樣本與最優解之間的接近程度可以表示為

(17)

式中:Fjideal和Fjnon-ideal分別為理想解和非理想解。

基于上述熱力學和優化模型,制定了如圖3所示的ORC的詳細設計和優化流程。

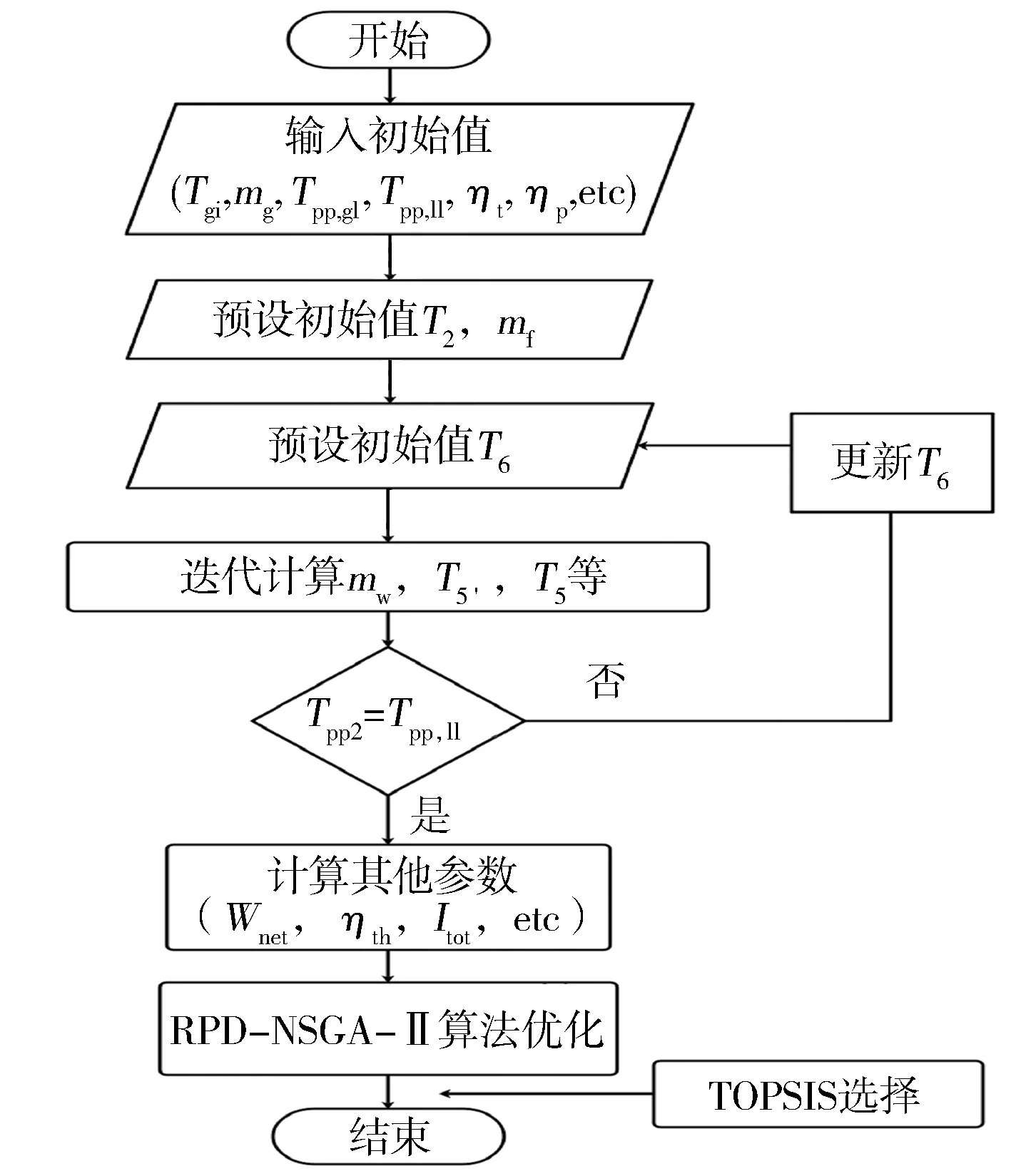
圖3 ORC的計算流程

2.4 優化結果分析

通過platemo平臺[20]利用RPD-NSGA-Ⅱ算法對ORC系統的熱力學性能進行多目標優化。表7對比了PSO算法[11]和NSGA-Ⅱ算法[15],以及基于NSGA-Ⅱ算法改進的NSGA-Ⅱ-SDR(strengthened dominance relation)算法[21]和RPD-NSGA-Ⅱ算法[16]。結果表明:RPD-NSGA-Ⅱ算法的IGD值和與真實數量的誤差都最小,所以該算法的性能最好。值得注意的是,雖然NSGA-Ⅱ-SDR也對NSGA-Ⅱ算法進行了改進,但IGD值和誤差明顯高于NSGA-Ⅱ算法,這說明雖然經過算法改進,但是對于ORC系統的性能優化并不適用。最后經過RPD-NSGA-Ⅱ算法得到帕累托前沿,然后通過TOPSIS可從Pareto前沿中選取熱力性能的綜合最優解。

表7 優化算法的評價指標比較

圖4示出了通過高維多目標優化(EMO)和TOPSIS選擇的ORC系統熱力學多目標優化過程。由圖可知,第一次迭代的初始種群分布比較密集,等迭代次數分別達到50次和100次,可以發現種群多樣性和收斂性明顯得到優化。Izon與Wnet呈正相關,而ηth與Wnet和Izon呈負相關。表8列出了基于高維EMO和TOPSIS選擇的熱力學結果。基于平衡ηth,Wnet和Izon的TOPSIS選擇方法,最佳ηth,Wnet和Izon分別為24.07%,72.36 kW和44.66 kW,結合式(9)和式(10)可知此時柴油機廢氣能量回收率為12.5%。若基于平衡Wnet和ηth選擇,則Wnet增加了12.22%,而ηth卻減少6.56%,相應地Izon增加了16.61%。若基于平衡Wnet和Izon選擇,則Wnet和Izon分別增加0.21%和0.76%,相應地ηth減少0.37%。值得注意的是,若基于平衡ηth和Izon選擇,ηth增加了10.72%,而Izon減少了83.61%,相應地Wnet減少了86.01%。因此,對ORC熱力學的分析表明,減少Izon勢必會使ηth增加、Wnet降低,無法獲得同時滿足三個性能指標的參數,但基于不同權重的分析可以給出實際工程更多選擇。

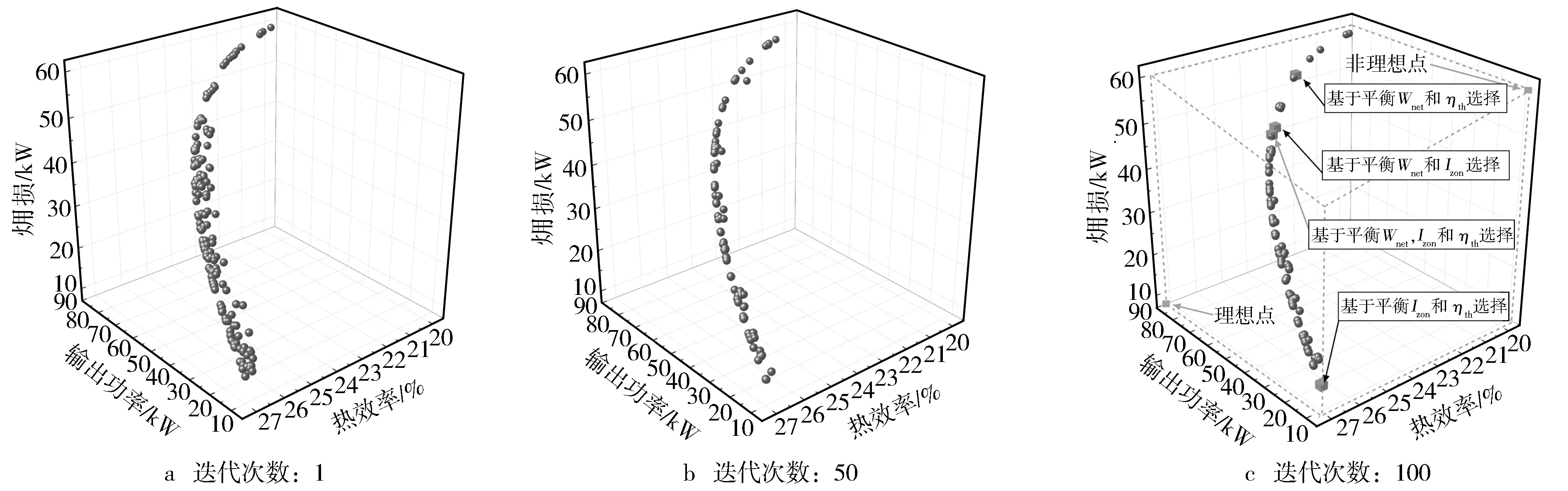
圖4 基于高維EMO平衡權重的ORC系統熱力學分析

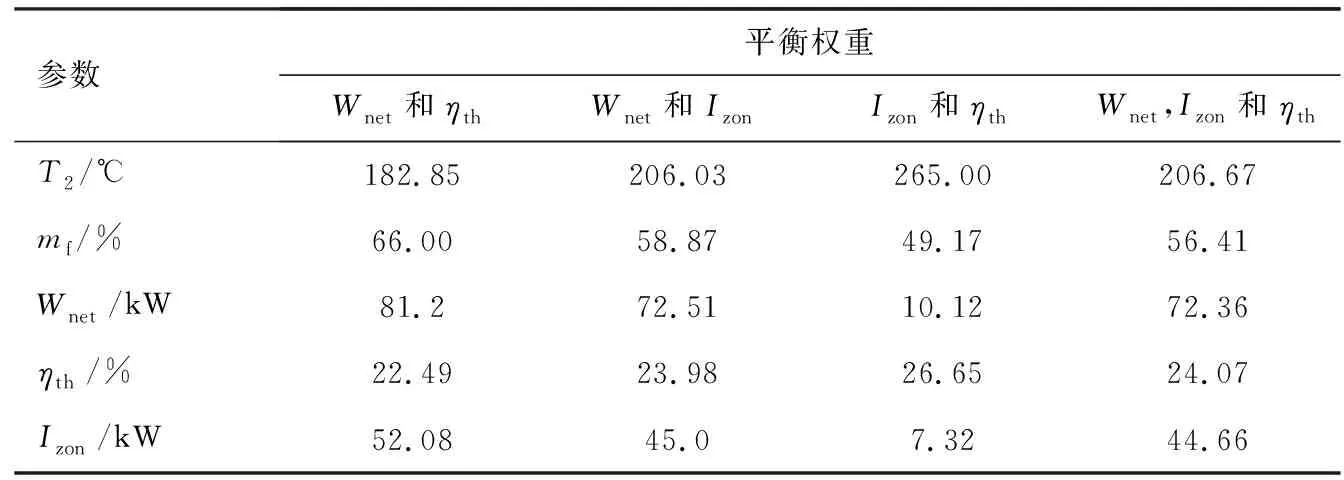
表8 基于高維EMO平衡權重和TOPSIS選擇的熱力學參數

圖5示出了基于不同評價指標的非平衡權重分析情況。由圖5a可見,Wnet和ηth的非平衡權重關系呈負相關。這說明Wnet高時ηth不理想,而ηth高時Wnet不高,可認為ηth和Wnet之間是支配性關系。由圖5b可見,基于ηth和Izon的非平衡權重關系呈負相關,因此,優化ηth總能減少Izon,而Izon的減少也能增加ηth,ηth和Izon之間是支配性的關系。由圖5c可見,基于Wnet和Izon的非平衡權重關系呈正相關,因此,優化Wnet和優化Izon是相互矛盾的,Wnet的提高是以增加Izon為代價的,而Izon的減少是以減少Wnet為代價的,所以Wnet和Izon之間是非支配性的關系。

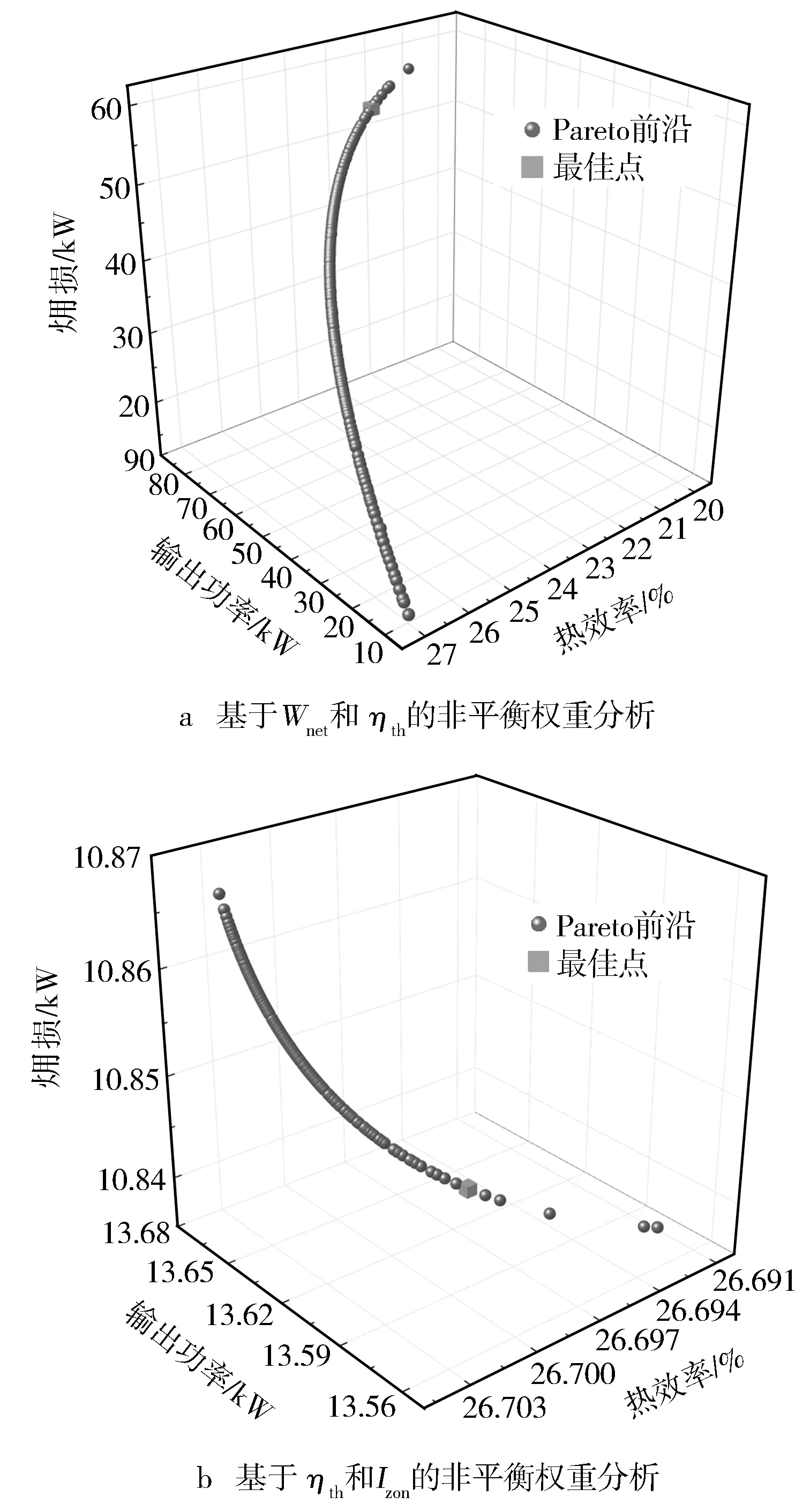
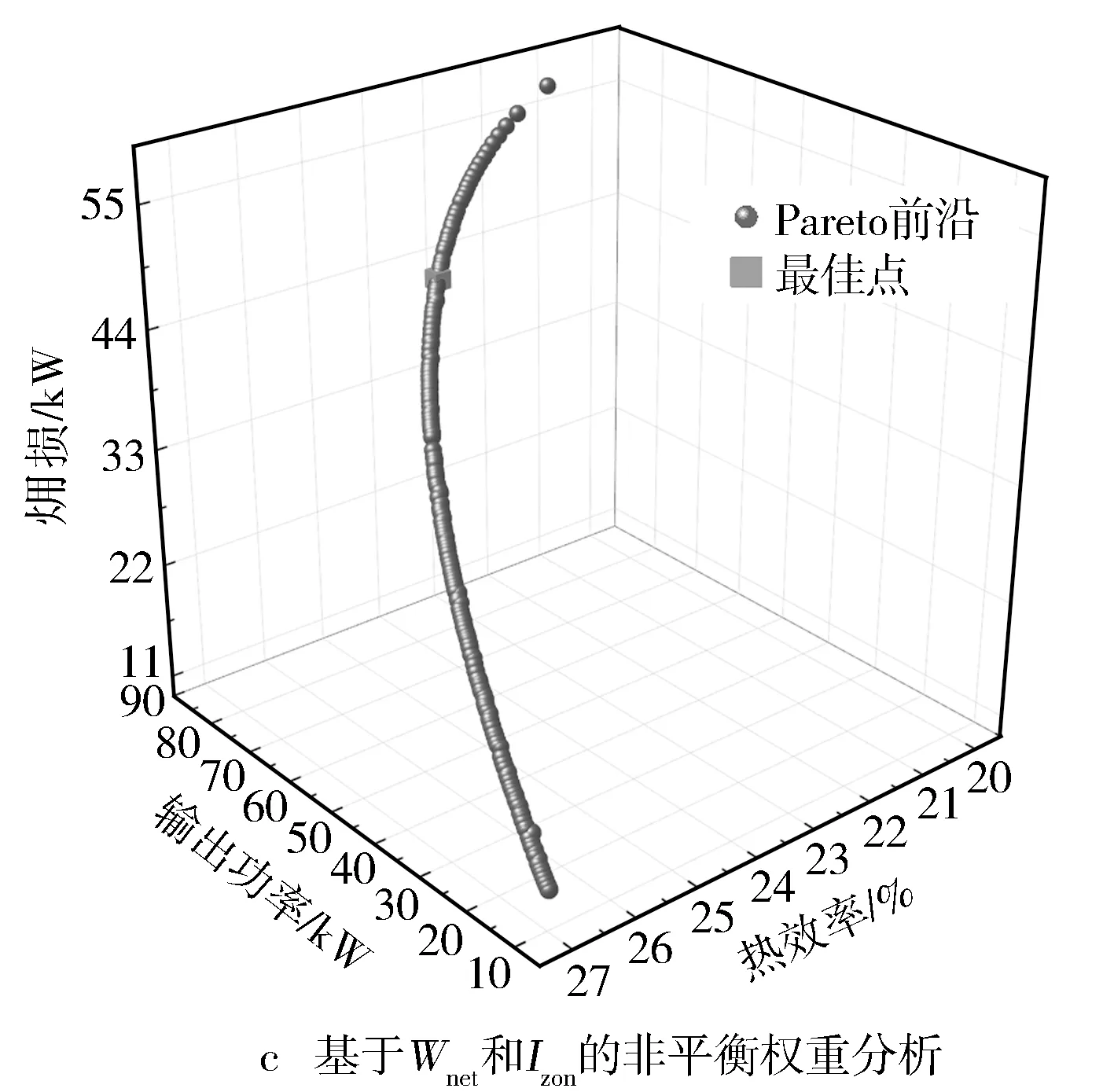
圖5 基于不同評價指標的非平衡權重的ORC系統熱力學分析

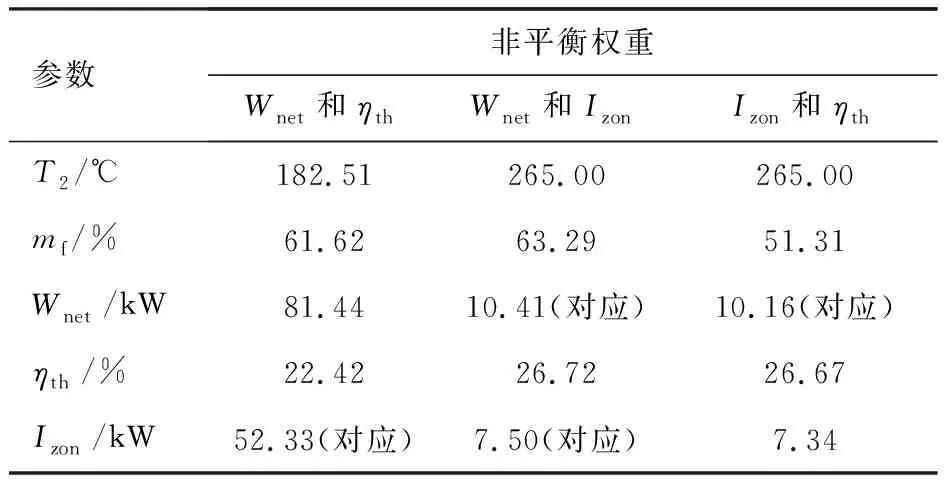
表9 基于不同評價指標的非平衡權重的熱力學性能

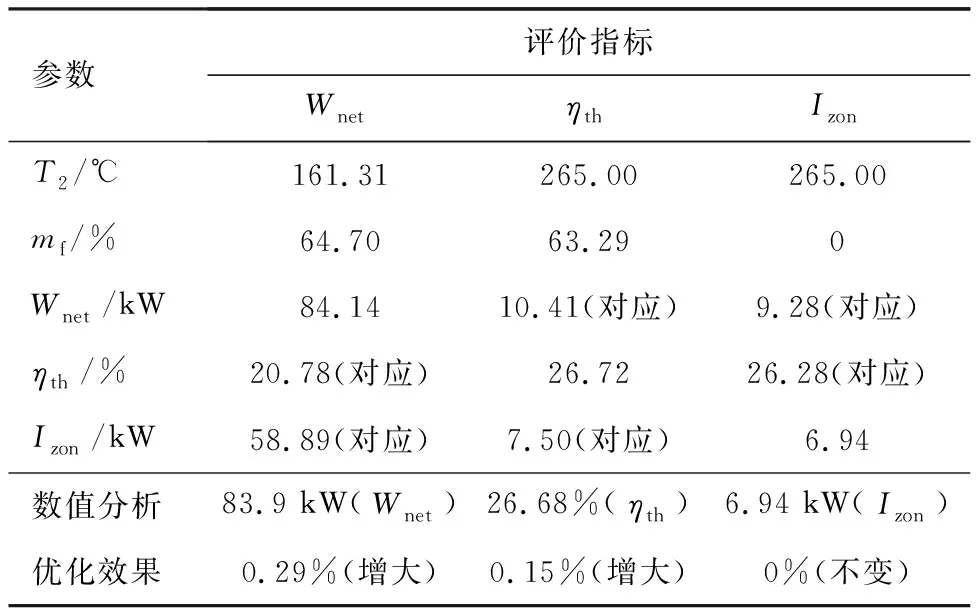
表10 基于單一評價指標的熱力學參數

3 結論