基于改進粒子群算法的物流供應鏈結構優化研究

殷聿明

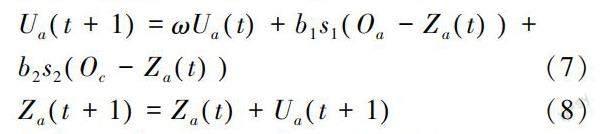
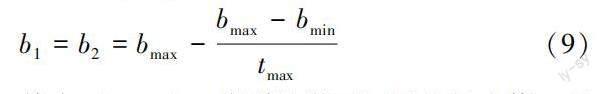
摘要：為了在降低物流供應鏈運作成本的同時，提升物流供應鏈服務用戶滿意度，文章研究基于改進粒子群算法的物流供應鏈結構優化方法。該方法在探討物流供應鏈結構成員信息后，構建物流供應鏈運作成本最小化、用戶滿意度最大化的目標函數，將粒子群算法中學習因子，使用線性調節的方式進行改進，由改進后粒子群算法尋優獲取可實現運作成本最小化、用戶滿意度最大化的物流供應鏈結構優化配置措施。研究結果顯示：該方法使用后，物流供應鏈運作成本得以降低，用戶滿意度得到提升，該方法有效可行。

關鍵詞：改進粒子群算法，物流供應鏈，結構優化，成本最小化

中圖分類號：TH166

文獻標識碼：A

文章編號：1674-9545（2023）03-0027-（05）

DOI：10.19717/j.cnki.jjun.2023.03.006

物流供應鏈結構優化管理屬于一種集成性管理，它主要用于提升整個物流供應鏈的運作效率與效益，且對企業之間協作十分重要^[1]。以往物流供應鏈結構管理方法中，主要使用縱向一體化管理方法，沒有從整體結構優化角度分析物流供應鏈結構優化問題。如參考文獻[2]中，李懷棟等人使用第二代非支配排序遺傳算法，尋優求解可實現港機制造企業供應鏈運作成本最小化的優化方案，此方法雖然能夠降低供應鏈運作成本，但忽視用戶的購物感受，且鏈上各個成員企業僅關注自己的物流信息，協作性較差，資源利用率有待提升。參考文獻[3]中，楊曉英等人以節省物流成本為目的，提出供應鏈物流協同優化方法，此方法主要針對于物流問題的協調控制優化。而物流供應鏈結構管理屬于集成性管理問題，管理過程中，需要完成物流、信息流、資金流等多種問題的集成性分析，其結構優化的目的是使用最少運作成本，實現用戶滿意度最大化^[4]。因此，文章研究基于改進粒子群算法的物流供應鏈結構優化方法，利用改進粒子群算法的多目標優化能力，實現物流供應鏈結構全面優化。

1物流供應鏈結構優化方法

1.1物流供應鏈結構與優化技術架構分析

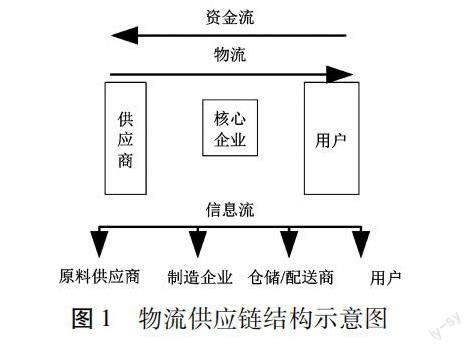
在合作競爭式市場環境中，物流供應鏈的結構配置十分重要，圖1為物流供應鏈結構示意圖。物流供應鏈結構屬于網鏈式結構，供應商企業、核心企業、用戶都可看作一種節點，節點之間存在需求和供應的關聯性。核心企業是用于銷售產品的企業，屬于銷售商，在供應鏈結構優化中，此企業屬于信息調度方。當出現物流需求，核心企業需要以物流供應鏈智能分工、協作的方式，保證供應鏈正常運行。

由圖1可知，物流供應鏈涉及物流、信息流、資金流三種流信息^[5]，物流信息覆蓋供應鏈整個網鏈，信息流與資金流分別表示物流需求與供應鏈運作成本信息。結合物流供應鏈結構信息，文章研究一種基于改進粒子群算法的物流供應鏈結構優化方法，此方法的技術架構如圖2所示。物流供應鏈結構優化時，主要涉及的配置對象分別是提供原料的供應商（供應商的供應商）、制造企業（加工廠）、倉儲/配送商、用戶，優化措施為構建加工廠、倉庫。物流供應鏈結構優化時，需要嚴格遵守產品制造數量約束、庫存約束、制造企業運出產品數量約束、配送產品數量約束條件，從而保證可實現物流供應鏈運作成本最小化、用戶滿意度最大化。

1.2基于改進粒子群算法的供應鏈結構優化配置方法

1.2.1供應鏈結構優化配置目標函數設計 文章分析的供應鏈結構優化配置問題中，供應鏈結構中主要涉及的配置對象分別是原料供應商、制造企業、倉儲/配送商、用戶。為利于分析，文章假定供應鏈結構優化配置目標函數設計時，用戶需要的產品類型為單一品種。圖3是基于改進粒子群算法的供應鏈結構優化方法運行時，簡化式供應鏈結構示意圖。

在圖3的供應鏈結構優化配置工況中，基于改進粒子群算法的供應鏈結構優化方法運行時，在設計供應鏈結構優化配置目標函數之前，需先設置以下幾個假設條件：

（1）整個物流供應鏈結構主要由產品需求拉動，需求量已知，用戶滿意度上下限已知；

（2）產品在供應鏈結構中的損耗忽略不計；

（3）整個物流供應鏈結構優化過程中，涉及的運作成本數據為已知數據。

供應鏈結構優化配置目標函數設計時，設置產品原料的供應商是j∈J，制造企業所在地與倉儲/配送商所在地分別是i∈I、h∈H；用戶是r∈R。產品運輸方式是n∈N。用戶r年度購買產品數量最大值是C_r；制造企業i年度生產能力（產能）最大值、倉儲/配送商h的倉儲能力最大值依次是Q_imax、V_hmax；原料單位成本、構建加工廠的年度固定成本依次是r^′_j、q^′_j；構建倉庫的年度固定成本、加工廠的運作成本依次是v^″_h、q_i；單位倉儲成本、自原料供應商j運輸至倉儲/配送商i的運輸成本依次是v_h、q_ji；使用運輸方式n，在制造企業i配送至倉儲/配送商h的單位運輸成本是v_ihn；使用運輸方式n，在h配送至用戶r的單位運輸成本是v_hrn。自j運輸至i的原料產品數量、由運輸方式n自i運輸產品至h的產品數量依次是y_ji、y_ihn；由運輸方式n在h運輸至用戶r的產品數量是y_hrn。用戶r需要的產品數量是x_r。

則物流供應鏈結構優化配置目標函數是：

式（1）表示物流供應鏈運作成本Ω最小化，式（2）表示用戶滿意度Ψ最大化。φ_r、φ_h依次是表示供應鏈結構優化配置措施，φ_r數值是1時，表示需要構建加工廠。φ_h數值是1時，表示需要構建倉庫。

1.2.2供應鏈結構優化配置約束條件設計 （1）制造企業制造的產品數量約束。制造企業制造的產品數量Q_i，不能大于自身產能最大值Q_imax。則：

（2）庫存約束。庫存產品數量V_h不可大于庫存容量最大值V_hmax，則：

（3）制造企業運出產品數量約束。制造企業可運出產品數量必須等于產能數量，則：

（4）配送產品數量約束。配送至用戶的產品數量需要大于用戶需求數量，則：

1.2.3改進粒子群算法的供應鏈結構多目標優化求解 粒子群算法屬于人工智能算法，能夠以迭代更新的方式提取問題（物流供應鏈運作成本最小化，用戶滿意度最大化）最優解，下文簡稱物流供應鏈結構多目標優化解，此算法把各組物流供應鏈結構多目標優化解設成粒子個體，通過迭代更新的方式，變化粒子個體位置，對比適應度函數的大小，分析物流供應鏈結構多目標優化解是否滿足要求。動態迭代時，隨機設置各個粒子個體位置與速度，尋優時，粒子個體會自主分析自己和最優解之間的距離，以及需要運行的角度，并實時更新調整，便可獲取物流供應鏈結構多目標優化的最優解。

此算法中，代表物流供應鏈結構多目標優化解的粒子個體速度、位置更新方法是：

其中，a表示第a個粒子的序號；U_at+1、U_at依次是迭代更新前后粒子速度；Z_at+1、Z_at依次是迭代更新前后粒子位置；ω、O_a依次是慣性因子、全局最優位置，全局最優位置表示多個物流供應鏈結構優化解對比后，所得全局最優解；O_c是粒子個體自身最優位置，表示某物流供應鏈結構優化解，與自身多迭代進程中優化結果對比后，所得局部最優解；b₁、b₂是學習因子；s₁、s₂是隨機數；t是迭代次數。

各粒子位置變化時，使用適應度函數便可判斷目前優化解的優劣，調節目前粒子位置與速度，便可提取物流供應鏈結構多目標優化的全局最優解。

學習因子能夠控制粒子自身信息和種群信息，隨機數能夠優化種群多樣性，保證物流供應鏈結構多目標優化解的多樣化。如果學習因子過于固定，便會導致粒子處于局部最優模式，為此，文章改進粒子群算法，同時調節b₁、b₂速率，則：

其中，b_min、b_max分別是學習因子的最小值、最大值；t_max是迭代次數最大值。

式（7）中b₁s₁O_a－Z_at、b₂s₂O_c－Z_at在不同迭代過程時，對粒子群算法存在不同影響。迭代次數增多時，粒子全局尋優能力需要提升，局部尋優能力需要衰減，此時才能保證算法在初始化過程中，保持較好的收斂性。則：

其中，b_1max、b_1min依次是b₁的最大值與最小值；b_2max、b_2min依次是b₂的最大值與最小值。式（10）屬于線性遞減處理，式（11）屬于線性遞增處理。

綜上所述，改進粒子群算法的供應鏈結構多目標優化求解步驟為：

（1）將物流供應鏈結構多目標優化解集合編碼為粒子種群，并隨機設置粒子種群位置與速度；

（2）運算代表物流供應鏈結構多目標優化解的各個粒子適應度，適應度計算方法是：

（3）把代表物流供應鏈結構多目標優化解的各個粒子目前適應度，和自己最優位置適應度進行對比，如果目前位置適應度更好，便將此位置的優化解，作為物流供應鏈結構多目標優化的局部最優解；

（4）把代表物流供應鏈結構多目標優化解的各個粒子適應度，和其他粒子適應度進行對比，如果目前粒子適應度更好，便將此粒子作為物流供應鏈結構多目標優化的全局最優解；

（5）使用式（10）、式（11）對學習因子進行線性調節，并更新粒子速度與位置；

（6）分析迭代次數是否為最大值，如果是，便輸出物流供應鏈結構多目標優化的全局最優解，反之跳轉至步驟（2）。

2仿真實驗

2.1實驗設置

以某地區水果物流供應鏈為研究對象，在優質水果培育區域，設置水果加工廠與倉庫，主要銷售的用戶區域數量是8個，簡稱為r₁～r₈，水果原料供應商即為產地，其數量是4個，簡稱為i₁～i₄。在4個水果原料供應商i₁～i₄采購水果原料，需要設置多個水果加工廠，倉儲/配送商的數量是2個，數量不足，需要設置合理的倉庫用于存儲水果。在此工況中，使用文章方法進行物流供應鏈結構優化，以期實現成本最小化、用戶滿意度最大化。

表1是實驗區域的水果銷量詳情，表2是原料水果的產能與成本詳情。水果加工制造廠的Q_imax=1×10⁵t，倉儲/配送商的V_hmax=1×10⁵t。結合表1所示用戶歷史銷量數據可知，實驗區域用戶對水果產品的購買量，超出此地區水果物流供應鏈的能力，為此，需要對此供應鏈結構進行優化配置。

2.2物流供應鏈結構優化效果分析

為測試文章方法使用效果，先分析文章方法對粒子群算法改進前后，算法的迭代收斂效果。測試結果如圖4所示。由圖4測試結果顯示：文章方法改進粒子群算法前，算法需要迭代至少10次，才能獲取適應度函數值最優的供應鏈結構優化最優解；文章方法改進粒子群算法后，算法僅需8次迭代便可獲取供應鏈結構優化最優解，對比之下，粒子群算法改進存在必要，且能夠提高供應鏈結構優化最優解的適應度，保證結構優化效果最佳。由此可知，文章方法可使用改進粒子群算法求解供應鏈結構優化問題。

則文章方法對3.1小節所述實驗工況的優化方案如表3、表4所示，數值1表示需要構建，數值0表示不需要構建。

則在表3、表4所示配置方案的優化處理下，對比分析實驗區域的物流供應鏈結構優化前后，供應鏈運作成本與用戶滿意度變化。用戶滿意度的計算方法是：

如果Ψ數值小于0.0，則表示產品供不應求，用戶滿意度也由此受到負面影響。

則文章方法優化前后，物流供應鏈運作成本、用戶滿意度變化如圖5、圖6所示。物流供應鏈運作成本以2022年度的6月2日、4日、6日、8日、10日、12日、14日、16日的核心企業物流供應鏈運作數據為例進行分析。用戶滿意度以表1中r₁～r₈的數據為例進行分析。由圖5、圖6可知，文章方法優化處理下，物流供應鏈運作成本減少，用戶滿意度提升，說明文章方法能夠以物流供應鏈運作成本最小化、滿意度最大化為目標，優化配置研究區域的物流供應鏈結構，文章方法可用于物流供應鏈結構優化任務。

3結論

文章對物流供應鏈結構優化問題進行深入研究，提出了基于改進粒子群算法的物流供應鏈結構優化方法，此方法和其他方法的不同之處在于，其能夠以物流供應鏈運作成本最小化、用戶滿意度最大化的方式，實現企業與用戶利益雙優化。且此方法在優化配置物流供應鏈結構時，改進了粒子群算法，以此提高物流供應鏈結構優化配置方案的尋優效率。在實驗中，文章方法被驗證可用于物流供應鏈結構優化任務，物流供應鏈運作成本減少，用戶滿意度提升，說明文章方法的使用性能，可滿足物流供應鏈結構優化需求。

參考文獻：

[1]高吉冰，鄭瀾波.基于Benders分解的煤炭供應鏈網絡維護調度優化[J].武漢理工大學學報（信息與管理工程版），2020，42（3）：227.

[2]李懷棟，胡堅堃，黃有方.基于改進NSGA-Ⅱ的港機制造企業供應鏈網絡優化[J].上海海事大學學報，2021，42（4）：92.

[3]楊曉英，王金宇.面向智能制造混流生產的供應鏈物流協同策略[J].計算機集成制造系統，2020，26（10）：2877.

[4]趙罡.基于MILP模型的氫氣供應鏈路徑優化[J].天然氣工業，2022，42（7）：118.

[5]王英輝，吳濟瀟，趙書潤，等.基于第四方物流的運輸型物流樞紐整合優化[J].鐵道運輸與經濟，2022，44（6）：56.

（責任編輯 王一諾）