SSA不全等三角形的性質探究
黃會


摘 要: 眾所周知,滿足 ASA 、 AAS 、 SAS 、 SSS 的兩個三角形都是全等的,這些全等三角形的性質相當完善,但兩個三角形滿足 AAA 或 SSA 卻不一定是全等的,那這樣的兩個三角形又有什么樣的性質呢?滿足 AAA 的兩個三角形是相似的,這樣的兩個三角形的性質也是完備的.那么滿足 SSA 的不全等的兩個三角形又有怎樣特殊的性質呢?文章從高線、角、邊、外接圓半徑四個角度探究其性質.
關鍵詞: ?SSA ;不全等;性質;三角形
1 問題的提出
兩個三角形全等有很多種判定方法,但 SSA 作為邊角組合中不能判定兩個三角形全等的特殊存在.那么是不是所有滿足 SSA 的兩個三角形都不全等?已有相關研究如周玲[1]、曹松峰[2]、陳月紅[3]等人對此進行了探索,答案均是否定的.
由判定倒推性質,全等三角形的性質目前較為完備,但滿足 SSA 的不全等的兩個三角形又有怎樣特殊的性質呢?這個問題目前鮮有人涉獵.而回應該問題則從不全等的視角進一步豐富了 SSA 的性質.這也是研究的緣起.
2 性質探究及應用
2.1 性質探究
本文將從高線、角、邊、外接圓半徑四個角度探究滿足 SSA 但不全等的兩個三角形之間的性質.
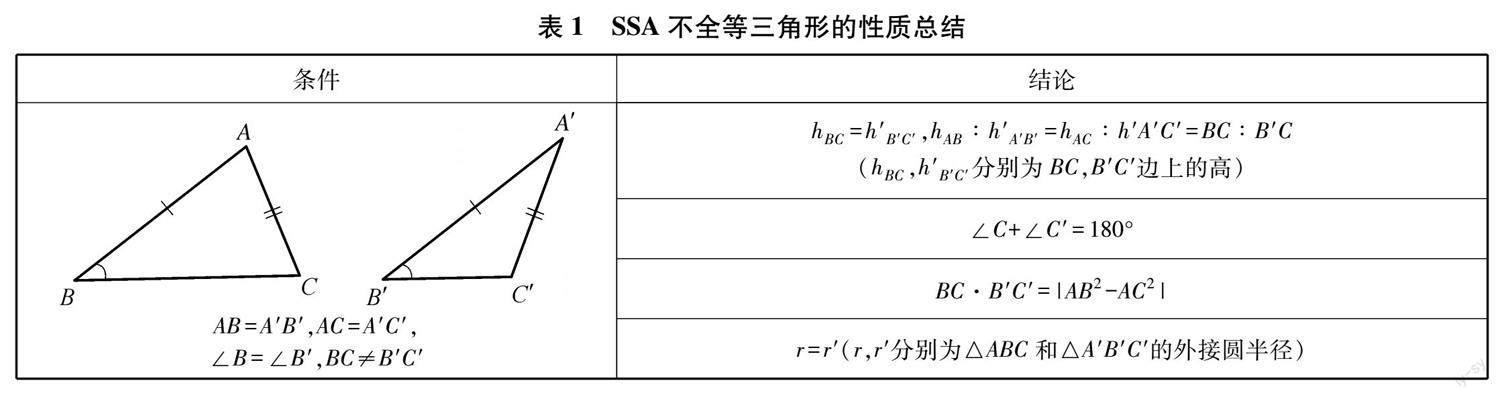
性質1: ?滿足 SSA 但不全等的兩個三角形不相等的第三邊上的高相等,相等邊上的高之比等于不相等的邊之比.
已知:如圖1,AB=A′B′,AC=A′C′,∠B=∠B′,BC≠B′C′,AD,BE,CF為△ABC的高,A′D′,B′E′,C′f ′為△A′B′C′的高.
求證:AD=A′D′,BE∶B′E′=CF∶C′F′=BC∶B′C′.
證明:易證△ABD≌△A′B′D′( AAS ),則AD=A′D′.
∵S △ABC= 1 2 BC·AD,S △A′B′C′= 1 2 B′C′·A′D′,
∴S △ABC∶S △A′B′C′=BC∶B′C′.
∵S △ABC= 1 2 AC·BE,S △A′B′C′= 1 2 A′C′·B′E′,
又∵AC=A′C′,∴BE∶B′E′=BC∶B′C′.同理可得,CF∶C′F′=BC∶B′C′.
性質2: ?滿足 SSA 但不全等的兩個三角形等角的相等鄰邊所對的角互補.
已知:如圖2,AB=A′B′,AC=A′C′,∠B=∠B′,BC≠B′C′.
求證:∠C+∠C′=180 ° .
證明:平移△A′B′C′,使AB與A′B′、∠B與∠B′重合.
易知B(B′)、C、C′三點共線.
∵AC=A′C′,即AC=AC′,∴∠1=∠C.
又∵∠1+∠2=180 ° ,∴∠C+∠2=180 ° ,即∠C+∠A′C′B′=180 ° .
性質3: ?滿足 SSA 但不全等的兩個三角形不相等的第三邊的乘積等于較大等邊與較小等邊的平方差.
已知:如圖3,AB=A′B′,AC=A′C′,∠B=∠B′,BC≠B′C′.
求證:BC·B′C′=AB2-AC2.
(不妨設BC>B′C′,AB>AC.)
證法一
證明:分別過點A,A′作AD⊥BC交BC于D,作A′D′⊥B′C′交B′C′于D′.
由性質1知AD=A′D′. 易證 Rt △ACD≌ Rt △A′C′D′( HL ) ,則CD=C′D′.
在 Rt △ABD中,BD2+AD2=AB2;①
在 Rt △ACD中,CD2+AD2=AC2;②
①-②得,(BD+CD)(BD-CD)=AB2-AC2.
又∵BC=BD+CD,B′C′=B′D′-C′D′=BD-CD,
∴BC·B′C′=AB2-AC2.
證法二
證明:平移△A′B′C′,使AB與A′B′、∠B與∠B′重合,如圖4.
易知B(B′),C,C′三點共線.
以A為圓心,AC為半徑畫圓,交射線BA于E,F兩點,連接AC′,FC.
∵四邊形EC′CF為圓A的內接四邊形,∴∠1+∠FCC′=180 ° .
又∵∠1+∠2=180 ° ,∴∠2=∠FCC′.
又∵∠B′=∠B,∴△B′EC′∽△BCF.
∴ B′E BC = B′C′ BF ,即BC·B′C′=B′E·BF.
又∵B′E=AB-AE=AB-AC,BF=AB+AF=AB+AC,
∴BC·B′C′=(AB+AC)(AB-AC)=AB2-AC2.
性質4: ?滿足 SSA 但不全等的兩個三角形外接圓半徑相同.
已知:如圖5,AB=A′B′,AC=A′C′,∠B=∠B′,BC≠B′C′,r,r′分別為△ABC和△A′B′C′的外接圓半徑.
求證:r=r′.
證明:作圓O直徑AD,連接CD.則∠B=∠D.
∵AD為圓O直徑,∴∠ACD=90 ° .
∵ sin ?D= AC AD ,∴AD= AC ?sin ?D = AC ?sin ?B . ∴r= AD 2 = AC 2 sin ?B .同理,r′= A′C′ 2 sin ?B′ .
∵AC=A′C′,∠B=∠B′,∴r=r′.
事實上,一個三角形一角及其對邊確定,這個三角形的外接圓半徑是確定的[4].
3 性質應用
例 ??已知:如圖6,AC平分∠BAD,BC=CD,AC,BD相交于點E.
求證:BE·DE=AE·CE.
證明:∵AC平分∠BAD,∴∠1=∠2.
∵∠1=∠2,BC=CD,AC=AC,
∴∠ABC+∠ADC=180 ° .( SSA 不全等的三角形性質2)
易得A,B,C,D四點共圓. ∴∠1=∠3.
又∵∠AEB=∠DEC,∴△ABE∽△DCE. ∴ BE CE = AE DE ,即BE·DE=AE·CE.
本題證明中的四點共圓亦可證明 SSA 不全等的兩個三角形的外接圓半徑相等,即 SSA 不全等三角形的性質4.
4 研究結論
通過以上探究,本文得到滿足 SSA 但不全等的兩個三角形有以下四條性質:不相等的第三邊上的高相等,相等邊上的高之比等于不相等的邊之比;等角的相等鄰邊所對的角互補;不相等的第三邊的乘積等于較大等邊與較小等邊的平方差;外接圓半徑相等.詳見表1.
總體來看,本文探究了滿足 SSA 但不全等的兩個三角形的性質,在理論上豐富了 SSA 的知識體系,在實踐教學中有助于更好地理解 SSA ,利用本文所獲得的結論亦可快速解答相關題目.
參考文獻:
[1] 周玲.增加一節“SSA”探究課又何妨?[J].中學數學教學參考,2016,643(17):69 70.
[2] 曹松峰. SSA與三角形全等的判定[J].中學生數理化(八年級數學)(配合人教社教材),2019,1165(9):8 9.
[3] 陳月紅.“SSA”全等條件的深度探究[J].理科考試研究,2016,520(16):16 17.
[4] 常學源.探求三角形的外接圓半徑[J].中學生數理化(學研版),2015,105(6):14.

