基于身份的群組密鑰分發方案

王后珍 秦婉穎 劉 芹,3 余純武 沈志東

1（武漢大學國家網絡安全學院 武漢 430072）

2（先進密碼技術與系統安全四川省重點實驗室（成都信息工程大學） 成都 610054）

3（空天信息安全與可信計算教育部重點實驗室（武漢大學） 武漢 430072）

4（武漢大學計算機學院 武漢 430072）

隨著互聯網技術的迅速發展和社交軟件的大量涌現，人們越來越依賴于即時通訊軟件進行網絡在線交流.現代的即時通訊軟件不僅能提供私聊功能，還能夠提供群聊功能.無論是在工作場所還是學術領域，群聊在促進高效合作、提供知識交流平臺和增進人際互動等方面都發揮著積極作用.

網絡群聊為人們的生活帶來了便利的同時也帶來了一些安全問題.由于群聊中產生的消息在不安全的公開信道上傳輸，攻擊者可以通過竊聽信道來獲取某個用戶在群聊中發送和接收的消息，從而導致用戶隱私數據的泄露，給用戶造成損失.因此，為了保障群聊中發送和接收消息的安全性，需要采取有效措施.針對這一問題，常用的解決方法是在傳輸之前對群聊中傳遞的消息進行加密，然而，需要解決的問題是如何讓參與群聊的用戶具有一個相同的共享會話密鑰.

1976 年，Diffie 等人[1]提出了Diffie-Hellman 密鑰交換協議，用于在一對一通信中建立共享會話密鑰.然而，Diffie-Hellman 密鑰交換協議只能用于在2 個用戶之間建立共享密鑰，并不適用于群組密鑰的建立[2].

為了解決在多用戶場景下建立群組密鑰的問題，許多方案應運而生.建立群組密鑰的方案總體上可分為2 類，分別是群組密鑰協商方案和群組密鑰分發方案[3-5].

群組密鑰協商是由所有參與群組通信的用戶一起合作共建群組密鑰，不依賴于可信的中央權威機構，群組密鑰直接由群組內成員共同決定[6].根據群組密鑰類型的不同，這類方案分為對稱群組密鑰協商和非對稱群組密鑰協商[7-8].在對稱群組密鑰協商方面，自Ingemarsson 等人[9]提出通過擴展Diffie-Hellman密鑰交換協議來為n個參與者提供對稱群組密鑰的方案以來，許多學者對此進行了深入研究，并提出了構造各異的對稱群組密鑰協商方案.Naresh 等人[10]提出了一種基于集群的混合分層組密鑰協商框架，為大型無線自組織網絡中的安全組通信提供一個可擴展的解決方案；Xu 等人[11]提出了一種基于區塊鏈和令牌機制的匿名認證動態群組密鑰協商方案，用于提高工業5.0 中物聯網設備的群組通信效率并降低能耗；Lee 等人[12]提出了一種輕量級的匿名動態群組認證密鑰協商方案，使一組醫療傳感器設備能夠相互認證并協商一個共享會話密鑰，用于解決醫療物聯網中的傳輸安全問題.

非對稱群組密鑰協商由Wu 等人[13]首次提出，他們提出的是一種單輪的非對稱群組密鑰協商協議（Asymmetric Group Key Agreement，ASGKA），該協議允許1 組用戶只協商1 個共同的公共加密密鑰，然后每個用戶各自計算自己的解密密鑰，加密密鑰公開，任何人都可見，解密密鑰由各用戶秘密保存，但該方案不能抵御主動攻擊且只適用于成員不發生變化的靜態群組；隨后，Zhang 等人[14]對ASGKA 協議進行了擴展和改進，設計了一個基于身份的認證非對稱群組密鑰協商協議，該協議能夠抵御主動攻擊，且適用于成員可發生變化的動態群組；張啟坤等人[15]提出了一種應用于無線傳感網絡的簇間輕量級非對稱群組密鑰協商協議，用于建立安全高效的簇間傳感器節點之間的群組通信信道；Li 等人[16]提出了一種基于區塊鏈和屬性的非對稱群組密鑰協商協議，該協議實現了協議參與者的訪問控制，用于解決工業物聯網中的安全通信問題.

群組密鑰協商方案雖然能夠解決群組密鑰的建立問題，但也存在一些劣勢.在群組密鑰協商方案中，所有參與群組通信的用戶都必須參與群組密鑰生成過程，這意味著每個參與群組通信的用戶都必須執行一些計算，這些計算可能需要消耗大量的時間，并占用大量的內存和處理器資源；而且參與群組通信的用戶之間需要進行頻繁的消息傳遞和交互，從而增加通信開銷和延遲.此外，如果有任何一個用戶無法參與協商，整個協商過程可能會受到影響.

相比之下，群組密鑰分發方案能夠很好地規避這些劣勢.群組密鑰分發是由一個被稱為群組密鑰管理者（group key manager，GKM）的可信第三方確定群組密鑰，并安全地將群組密鑰分發給群組內所有成員[5]，不需要全部參與群組通信的用戶參與到群組密鑰的生成過程，用戶之間也不需要進行頻繁的交互，從而減少了時間、內存、處理器資源的消耗，降低了通信開銷和延遲.Guo 等人[17]提出了一種自愈群組密鑰分發協議，用于提高物聯網不可靠無線網絡中群組通信的安全性和效率；Meng 等人[18]提出了一種基于Shamir 秘密共享方案的群組密鑰分發協議，該協議將在線和離線概念引入群組密鑰分發，從而大幅度提升了群組密鑰響應和恢復的速度；Li 等人[19]提出了一種用于無人機自組織網絡的互愈群組密鑰分發方案，該方案能有效抵御各種攻擊；Jiao 等人[20]提出了一種計算高效的群組密鑰分發協議，用于解決移動終端在動態群組密鑰分發過程中的計算成本問題；Y?ld?z 等人[21]提出了一種基于物理不可克隆函數和中國剩余定理的輕量級認證群組密鑰分發協議，用于解決物聯網中的群組認證和密鑰管理問題；Xu等人[22]提出了一種應用于車載自組織網絡的批量認證群組密鑰分發協議，該協議結合了消息批量認證和群組密鑰分發，用于確保每個經過認證的車輛都能獲得相同的群組密鑰.

近年來，大量的群組密鑰分發方案都是針對物聯網應用場景而設計的，針對即時通訊群聊場景的方案卻相對較少.物聯網應用場景下，連接到物聯網的設備通常資源有限，需要設計輕量級高效的群組密鑰分發方案，而且由于設備通常由電池供電，因此要求密鑰分發方案不能消耗過多的電力[17]；同時鑒于物聯網網絡的分布式特性，群組密鑰協商比群組密鑰分發更適合物聯網環境[6].相比之下，在即時通訊群聊場景中，設備通常擁有更高的計算能力和更大的存儲空間，因此可以考慮構造更復雜的群組密鑰分發方案來建立群組密鑰，以保證安全性；而且由于在即時通訊群聊中，通常由群主等具有更高權限的用戶來管理群聊，采用群組密鑰分發更符合這一特點.

與此同時，群組密鑰分發方案通常在可擴展性和效率方面表現更出色，相較于群組密鑰協商方案而言也更適用于即時通訊群聊場景.而使用基于身份的密碼體制[23]不需要申請和交換公鑰證書，可以降低服務器管理密鑰的成本，簡化服務器管理密鑰的流程，適用于即時通訊軟件.本文提出了一個基于身份的群組密鑰分發方案，旨在解決即時通訊群聊場景下的通信安全問題.本文方案基于國密SM9 算法和多項式進行構造，將群組密鑰嵌入到橢圓曲線點與多項式系數中后進行分發；與文獻[17-22]中依賴可信第三方分發群組密鑰的方案不同，本文方案由群聊中的群主負責生成群組密鑰，并將群組密鑰分發給群聊內的所有群成員，以此實現了即時通訊群聊場景下的群組密鑰分發，保障了通信安全.

本文方案的優勢主要包括4 個方面：

1）基于身份的密碼體制.采用了基于身份的密碼體制，避免了公鑰證書機制，降低了密鑰管理的復雜性.

2）兼容性較好.本文提出的方案基于國密SM9算法構建，能更好地保障我國政府及企業的通信安全.

3）支持離線操作.在本文提出的方案中，群組密鑰分發操作僅要求群主在線，而其他群成員可以在群主分發群組密鑰時處于離線狀態，無需受到實時在線的限制.在上線之后，他們可使用接收到的信息，按照方案規定的計算方法，有效地獲取群組密鑰.

4）支持群組密鑰恢復.在即時通訊群聊場景下，本文方案支持在服務器上存儲群組密鑰分發階段由群主發送的參數，當群成員存儲在本地的群組密鑰丟失時，可向服務器請求這些參數以恢復丟失的群組密鑰.

1 預備知識

1.1 雙線性對

設G1和G2是2 個加法循環群，GT是一個乘法循環群，G1，G2，GT的階均為素數N，P1是群G1的生成元，P2是群G2的生成元，存在G2到G1的同態映射 ψ使得ψ(P2)=P1，雙線性對e:G1×G2→GT為滿足3 個性質的映射：

1）雙線性：對任意的P∈G1，Q∈G2，a，b∈ZN，有e([a]P,[b]Q)=e(P,Q)ab；

2）非退化性：e(P1,P2)≠；

3）可計算性：對任意的P∈G1，Q∈G2，存在有效的算法計算e(P,Q).

1.2 相關困難問題

本文所提方案的安全性基于橢圓曲線計算性DH（elliptic curve computational Diffie-Hellman，ECCDH）問題[24-25]的困難性，ECCDH 問題的定義為：

定義1.ECCDH 問題.設G1是一個N階的橢圓曲線群，P1是G1的生成元，G1上的ECCDH 問題就是隨機選擇x，y∈[1,N-1]，給定(P1,[x]P1,[y]P1)，計算[xy]P1.

定義2.ECCDH 假設.設G1是一個N階的橢圓曲線群，P1是G1的生成元，如果對于數值足夠大的安全參數k，任意概率多項式時間的敵手 A滿足：AdvECCDH(A)=Pr[A(G1,P1,[x]P1,[y]P1)=[xy]P1]≤ε(k)，其中，AdvECCDH(A)表示敵手 A解決ECCDH 問題的優勢，x，y∈[1,N-1]，ε(k)是可忽略的，則稱群G1滿足ECCDH 假設.

1.3 安全模型

本文借鑒了文獻[15,26]中的安全模型，在此基礎上給出了本文方案的參與者模型與敵手模型的形式化定義，以及要實現的安全目標.

定義3.敵手模型.本文只考慮被動敵手.通過定義一個挑戰者 C 與被動敵手 A之間的游戲來定義敵手模型，該模型中包含1 個群聊的成員（包括群主和普通群成員）的集合和1 個敵手 A，每個群聊成員被模擬成一個隨機預言機，該游戲的具體步驟為：

1）系統建立階段.挑戰者 C輸入安全參數λ運行系統建立算法，生成系統公共參數的集合params和密鑰生成中心（key generation center，KGC）的主私鑰ke. C 將params發送給敵手 A，并保存KGC 的主私鑰ke.

2）查詢階段.敵手 A可以通過執行查詢與挑戰者 C進行交互，敵手 A可以進行的查詢次數為多項式有界次.

2 基于身份的群組密鑰分發方案

本節將介紹本文基于國密SM9 算法提出的一種基于身份的群組密鑰分發方案.

本文提出的方案中共有3 個角色，分別是KGC、創建群聊的群主和群內的普通群成員.其中KGC 負責生成系統參數、用戶的長期私鑰和用戶的公開參數；群主負責產生群組密鑰并進行分發；普通群成員通過群主發送的參數來計算出群組密鑰.假設群主和普通群成員都是向KGC 注冊過的、可信任的用戶.在本節中將給出本文方案的群組密鑰分發階段、新成員加入群聊階段和老成員退出群聊階段的具體過程.

2.1 群組密鑰分發階段

假設存在一個群聊，該群聊由n+1 個用戶組成，分別表示為U0,U1,U2,…,Un，其中U0為群主，U1,U2,…,Un則為普通群成員.假設這n+1 個用戶均已向KGC注冊過且都是可信的.設這n+1 個用戶的身份標識符分別為ID0,ID1,ID2,…,IDn.在群聊開始前，為了保障群聊天消息的安全性，這些用戶需要共享一個群組會話密鑰，用于加密群聊天消息.

2.1.1 系統初始化

在這一階段，KGC 生成系統參數并為所有注冊用戶生成其長期私鑰和公開參數.需要說明的是，由于本文方案基于國密SM9 算法進行構建，因此這一過程和SM9 算法中系統加密主密鑰和用戶加密密鑰的產生流程[27]相同.

KGC 選擇一個大素數p和一個大素數N，然后選擇橢圓曲線E(Fp)上的N階循環子群G1和橢圓曲線E(Fp2)上的N階循環子群G2；令P1為群G1的生成元，P2為群G2的生成元.接下來KGC 構造一個雙線性映射e:G1×G2→GT.

KGC 隨機選擇一個數ke∈ZN作為主私鑰，然后計算Ppub-e=[ke]P1作為系統公鑰.隨后KGC 選擇2 個哈希函數H1:{0,1}*→ZN和H2:GT→Zq，q的值后續由群主來決定，并選擇用一個字節表示的加密私鑰生成函數識別符hid.KGC 公開{G1,G2,P1,P2,Ppub-e,e,H1,H2,N}作為系統參數，并秘密保存主私鑰.

對于每個注冊用戶Ui，KGC 計算dei=[ke×(H1(IDi||hid,N)+ke)-1]P2作為其長期私鑰，計算Qi=[H1(IDi||hid,N)]P1+Ppub-e作為其公開參數，然后通過一個安全的信道將dei和Qi發送給每個用戶Ui.當群成員加入群聊時，其對應的Qi會發送給群主U0.

2.1.2 群主生成群組密鑰并計算相關參數

此過程將群組密鑰由群主生成并分發給群成員.會話開始前，群主首先隨機生成一個比特長度為len的整數q，然后隨機生成一個比特長度為len的整數K作為群組密鑰，要求1 ≤K＜q.

為了將群組密鑰K分發給群內的其他n個成員，群主依次執行3 個操作.

1）生成n+1個隨機數rk∈[1,N-1]，并計算：

①Ck=[rk]Qk，0 ≤k≤n，Ck∈G1；

②hk=H2(e([rk]Ppub-e,P2))，0 ≤k≤n，1 ≤hk＜q；

2）隨機選擇R∈[1,q-1]，然后構造多項式，并計算出各項的系數：

3）將C1,…,Cn,an+2,…,a0和q廣播給群內的每個成員.

2.1.3 群成員計算群組密鑰

群內的每個用戶Uj(1 ≤j≤n)在收到攜帶參數的報文之后，通過3 個步驟計算得到群組密鑰K：

1）從報文中提取出Cj,an+2,…,a0和q，然后驗證Cj∈G1是否成立，若不成立則報錯并退出；

2）計算哈希值hj=H2(e(Cj,dej))；

3）計算群組密鑰K：

2.2 新成員加入階段

假設新用戶Un+1,Un+2,…,Un+m想要加入到該群聊中，他們的身份標識符分別為IDn+1,IDn+2,…,IDn+m，長期私鑰分別為den+1,den+2,…,den+m，公開參數分別為Qn+1,Qn+2,…,Qn+m.新用戶首先會向群主U0提交加群申請，提交申請時會同時發送自己的公開參數.若U0同意他們加入，就依次執行4 個操作.

1）重新生成一個比特長度為len的整數q′，然后隨機生成一個比特長度為len的整數K′作為群組密鑰，要求1 ≤K′＜q′.

2）重新生成n+m+1個隨機數∈[1,N-1]，并重新計算：

3）重新選擇一個隨機數R′∈[1,q′-1]，然后重新構造多項式并計算出各項的系數：

2.3 成員退出階段

假設該群聊中有t個用戶要退出群聊，那么在這t個用戶退出群聊之后，群主U0依次執行4 個操作重新分發新的群組密鑰給仍在群內的群成員.

1）重新生成一個比特長度為len的整數q′′，然后隨機生成一個比特長度為len的整數K′′作為群組密鑰，要求 1 ≤K′′＜q′′.

2）重新生成n-t+1個隨機數∈[1,N-1]，并重新計算：

若群主U0退出該群聊且在退出前未將群主權限移交給其它群成員，那么該群聊會立即解散，其余群成員在此之后無法通過該群聊進行通信，也無需重新建立該群聊的新的群組密鑰；若群主U0退出該群聊且在退出前將群主權限移交給其它群成員，那么此后將由新群主進行群組密鑰分發工作.

3 正確性與安全性分析

3.1 正確性分析

本節分析了本文方案的正確性.正確性是指若群內每個普通群成員計算無誤，則計算得到的群組密鑰與群主生成的群組密鑰一致.

定理1.本文方案滿足正確性.

證明.設群主U0生成的群組密鑰為K，q為與K比特長度相同且滿足1 ≤K＜q的整數，每個普通群成員Ui計算出來的群組密鑰為Ki.群主U0為每個Ui計算的hi為：

因此群內每個普通群成員Ui在本地計算出的群組密鑰和群主U0生成的群組密鑰是同一個密鑰.

綜上所述，本文提出的方案滿足正確性.證畢.

3.2 安全性分析

本節借鑒了文獻[15,26,28]對本文方案的安全性進行了分析與證明.

本文方案能夠抵抗被動攻擊，即一個被動敵手A無法通過監聽信道上傳輸的消息來獲取已建立的群組密鑰的相關信息.將本文方案的安全性歸約到ECCDH 問題上，通過這個困難問題來證明本文方案對被動敵手 A是安全的.

定理2.在1.3 節定義的安全模型下，如果存在一個被動敵手 A能在多項式時間內以不可忽略的優勢計算得到本文方案中的群組密鑰K，那么就可以利用敵手 A 來構造一個算法 B，使得算法 B能以不可忽略的優勢來解決ECCDH 問題.

證明.假設一個被動敵手 A能在本文方案中以不可忽略的優勢計算得到本文方案中的群組密鑰K.由于本文方案不滿足完美前向安全性，群內所有成員的長期私鑰不能泄露，因此規定敵手 A無法執行查詢與查詢.規定 A能執行的查詢只有算法 B利用敵手 A構造而來.設算法 B要解決的ECCDH 問題的一個實例為(P1,X=[x]P1,Y=[y]P1)，下面將展示算法 B如何調用敵手 A作為子程序來求解[xy]P1.

假設群聊共有n+1個參與者，其中1 人為群主U0，其身份標識符為ID0，剩下的n個人為普通群成員U1,U2,…,Un，他們的身份標識符為ID1,ID2,…,IDn.定義一個新的會話，該會話有一個唯一的標識符sids，算法 B將sids記錄下來.

1）初始化系統.設N是群G1，G2的階，P1表示群G1的生成元，P2表示群G2的生成元，雙線性對e:G1×G2→GT，B首先選取一個隨機數ke∈ZN作為系統主私鑰，并計算系統公鑰Ppub-e=[ke]P1，然后選擇一個哈希函數H0作為隨機預言機，最后設置系統參數為params={N,G1,G2,P1,P2,Ppub-e,e,H0}，并把params發送給敵手 A.

之后，算法 B按照1.3 節定義3 中定義的游戲與敵手 A進行交互.

①隨機生成一個整數q，然后隨機生成一個與q具有相同比特長度且滿足1 ≤K＜q的整數K；隨機選擇一個數R∈[1,q-1]，并生成n+1 個隨機數ri∈[1,N-1]；

然而定理2 與ECCDH 問題的假設相矛盾，因此由反證法可知，敵手 A贏得游戲的概率是可忽略的.證畢.

4 性能分析

4.1 理論分析

本節從理論的角度分析本文方案的存儲開銷和通信開銷.

假設運行本方案時聊天群內一共有n+1 個用戶U0,U1,U2,…,Un，其中U0為群主，其余n個用戶為普通群成員.假設每次分發的群組密鑰的比特長度都是相等的.

4.1.1 存儲開銷

表1 顯示了本文方案的存儲開銷.對于群主U0而言，由于rk(0 ≤k≤n)的值是每次分發群組密鑰時隨機選取的，Ck，hk(0 ≤k≤n)則是每次分發群組密鑰時根據rk計算出來的，an+2,an+1,…,a0的值是每次分發群組密鑰時根據hk構造而來的多項式的系數，這些值在每次進行群組密鑰分發時都是不一樣的，因此群主無需存儲這些臨時數據.群主需要存儲的只有自己的長期私鑰de0、群內n+1 個用戶的公開參數Qk和每次分發的群組密鑰K.由2.1.1 節可知，Qk是橢圓曲線E(Fp)上的點，它可被壓縮成一個長為個字節的字節串之后再進行存儲[29]；而de0是橢圓曲線E(Fp2)上的點，它可以被壓縮成一個長為個字節的字節串后再進行存儲[29].綜上可得，群主每次運行該方案時的存儲開銷為+n+2個字節.

Table 1 Storage Cost of Our Scheme表1 本文方案的存儲開銷

對于每個普通群成員而言，需要存儲的只有長期私鑰、公開參數和每次群主進行群組密鑰分發時計算出來的群組密鑰.因此每個普通群成員每次運行該方案時的存儲開銷為個字節.

4.1.2 通信開銷

表2 顯示了本文方案的通信開銷.每次分發群組密鑰時需要傳輸的數據是群主廣播的參數an+2,an+1,…,a0和C1,C2,…,Cn以及q，其中ai∈[1,q-1](0 ≤i≤n+2)，長度為lb(q-1)個比特，C1,C2,…,Cn均為橢圓曲線E(Fp)上的點，這些點可以分別被壓縮成一個長度為個字節的字節串后再進行傳輸，因此本文方案的通信開銷為個字節.

Table 2 Communication Cost of Our Scheme表2 本文方案的通信開銷

4.2 時間性能仿真實驗分析

本節通過仿真實驗對本文方案的時間性能進行了分析.

實驗中使用C++實現本文方案.選擇國密SM9標識密碼算法的曲線參數來實例化本文方案的系統參數，參照SM9 算法標準文檔中定義的哈希函數來實現本文方案中的哈希函數H1和H2，調用gmssl 庫函數執行點乘、點加和雙線性對運算，使用gmp 庫進行大數模乘、模加、模冪運算.測試平臺配置為11th Gen Intel?Core? i7-11 700 @ 2.50GHz × 2 的處理器，4 GB 的內存，Ubuntu 20.04.6 LTS 版本的64 位操作系統.

仿真選擇群主計算相關參數所需的平均時間和每個普通群成員計算出群組密鑰所需的平均時間作為評價指標，固定q與K的比特長度為128，分析當普通群成員人數n逐漸增大時對這2 個評價指標的影響.

本文方案中涉及6 種不同的運算，因此首先通過測試獲得了這6 種運算各自所需的平均時間，結果如表3 所示，其中 Zq表示模q的整數環.

Table 3 Average Time Required for Each of the Six Operations表3 6 種運算各自所需的平均時間

從表3 中可以看到，本文方案的時間開銷主要來自于雙線性對運算和群G1上的點乘運算.對于哈希函數H2，雖然其實現過程較為繁瑣，但由于不涉及復雜的運算和循環操作，因此執行時間很短，而 Zq上的大數加法、大數乘法、大數冪運算在gmp 庫的實現所花費的時間幾乎可忽略不計，因此執行后4 種運算所需的平均時間遠小于前2 種運算.

圖1 給出了當普通群成員人數增大時群主計算相關參數所需時間的增長情況.隨著人數的增加，群主需要計算的Ck，hk，ak的數量也隨之增加，要執行的雙線性對運算次數和G1上的點乘運算次數也增加，從而導致計算所花費的時間增加.從圖1 中可以看到，當人數超過70 時，群主計算所花費的時間超過了10 s，當人數超過450 時，群主計算所花費的時間超過了60 s.

Fig.1 Average time required for the group owner to calculate the relevant parameters圖1 群主計算相關參數所需的平均時間

圖2 給出了當普通群成員人數增大時每個普通群成員計算出群組密鑰所需的平均時間的變化情況.如圖2 所示，當普通群成員人數逐漸增大時，每個普通群成員計算出群組密鑰所需的平均時間的變化幅度很小，而且即使人數增長到500，計算時間仍然不超過0.1s，時間開銷完全在用戶可接受的范圍內.這是由于每個普通群成員每次執行該方案時只需計算1 個hj，計算量的增加僅僅是由于 Zq上的大數加法、大數乘法、大數冪運算的運算次數增加而導致的，而如表3 所示，這3 種運算的執行時間很短，因此帶來的時間消耗并不會大幅度增長，只會引起很小的變化.

Fig.2 Average time cost for each ordinary group member to calculate the group key圖2 每個普通群成員計算出群組密鑰的平均時間開銷

由圖1 和圖2 可知，本文方案在小規模群組中表現良好，但應用到大規模群組中時會出現群主分發密鑰時間較長的問題，但這種額外的時間代價是為了保障群聊消息的機密性而不可避免的.在實際應用中，通常情況下只需在建群之初運行一次本文方案，如果后續需要更新群組密鑰，只需令全群禁言并運行一次本文方案來重新分發群組密鑰.因此，相對于整個群聊會話的持續時間而言，本文方案所需的時間并不多.

當有新成員加入或有老成員退出時，群主需重新運行一次本文方案計算出新的群組密鑰，這種情況下帶來的計算開銷取決于群成員發生變動后群內共有的群成員數量.如圖1 所示，若群成員發生變動后群內成員總人數超過200，那么群主重新計算出新的群組密鑰所花費的時間會超過30 s.但是通常情況下群組成員并不會頻繁發生變動，因此群主不需要經常重新執行本文方案，也無需頻繁進行大量的計算操作.

綜上所述，為了保證群聊通信的安全性，本文方案產生的時間開銷是可以接受的.

4.3 方案的對比

本節從群組密鑰分發者的身份、預共享參數需求、群組成員交互需求和兼容性4 個方面將本文方案與文獻[17]方案、文獻[18]方案進行了對比，比較結果如表4 所示.其中分發者指的是負責產生群組密鑰并進行分發的實體，接收者指的是負責接收相關參數并計算出群組密鑰的實體.

Table 4 Comparison Between Our Scheme and Other Schemes表4 本文方案與其他方案的比較

從表4 中可以看出，相比于另外2 個方案采用可信第三方來分發群組密鑰，本文方案采用的是群組內具有更高權限的用戶來分發群組密鑰，賦予用戶更多的自主決策權，使得用戶可以控制群組密鑰的產生與分發，從而保證只有群組內成員能夠讀取群聊消息明文，而除了群組成員之外的任何人，包括服務提供商都無法讀取聊天內容的明文；相比于另外2 個方案，本文方案中接收者在群組密鑰分發階段之前不需要與分發者共享任何參數，這意味著接收者與分發者需要存儲和管理的參數更少，減輕了接收者與分發者的參數管理負擔；相比于文獻[18]方案中接收者在群組密鑰分發階段還需要額外向分發者發送消息，本文方案中在群組密鑰分發階段只有群主需要向群成員發送消息，而群成員無需再向群主發送任何消息，這意味著本文方案具有更少的交互和更低的通信成本；在兼容性方面，本文方案能兼容現有的算法標準，具有更好的兼容性.

本節還從密鑰管理的4 個角度和兼容性比較了本文方案與文獻[13]的方案，比較結果如表5 所示.

Table 5 Comparison Between Our Scheme and the Scheme Proposed in Reference [13]表5 本文方案與文獻[13]方案的比較

從表5 中可以看出，本文方案在群組密鑰管理上比Wu 等人的方案更有優勢，因為本文方案中無需向證書頒發機構注冊群組密鑰，簡化了密鑰管理的流程，密鑰分發的過程中也不要求除群主外的所有群成員都在線，靈活性更高；同時由于本文方案利用了SM9 算法進行構造，可以使用SM9 算法的國家標準來實現，兼容性更好，能夠更好地滿足國內的政府和企業對群聊通信安全的需求.

5 本文方案在具體場景下的應用

本節將詳細描述本文方案在具體場景下的應用方式.首先展示本文方案應用到一個具體的即時通訊群聊場景中時的運行流程；然后簡要介紹本文方案的一個外延應用，即本文提出的群組密鑰分發方案是如何在點對點通信場景下轉換成非對稱加密算法來進行端到端加密的；最后將本文簡要介紹的即時通訊軟件所采用的方案與本文方案進行對比，指出其不足之處，展現本文方案的優勢與創新點.

5.1 本文方案在即時通訊群聊場景下的運行流程

5.1.1 場景描述

假設某公司為了防止外人竊取公司數據而導致公司的機密信息泄露，打算開發一款局域網即時通訊軟件來進行公司內部員工之間的交流，讓公司內部產生的消息只在公司的局域網內流動，從而保證公司數據的安全.該公司有多個部門，每個部門人員較為固定，不會發生很大的變動，為了滿足部門內部的團隊溝通協作、發布通知公告等需求，該公司計劃在軟件中加入群聊功能，由部門領導創建群聊，部門其余員工加入群聊.為了保障這一功能的安全性，同時為了保證通信效率，需要對群聊消息采取對稱加密措施，此時如何讓群內所有用戶共享一個加解密群聊消息的對稱密鑰成為一個關鍵問題，在這種情況下，可以應用本文方案來解決這一問題.

5.1.2 方案應用

本節將詳細描述如何應用本文方案解決5.1.1 節所述的場景描述下的問題.假設公司內部員工都是可信的.

該公司內部人員首次使用他們的局域網即時通訊軟件時會先進行注冊.每個用戶Ui注冊時軟件客戶端會將用戶身份信息發送給局域網內的服務器，服務器為Ui生成其身份標識符IDi、公開參數Qi和長期私鑰dei，其中IDi作為公開信息與Ui的賬號綁定，然后將IDi，Qi，dei發送給Ui，同時保存IDi，Qi，dei.這一過程如圖3 所示.

Fig.3 Company employees register圖3 公司員工注冊

為了方便部門內發布公告、溝通工作事宜，某部門領導U0會作為群主創建群聊，然后將當前在該部門工作的全體員工加入群聊，初次創建群聊時，這一操作會強制將當前該部門所有的在職員工加入群聊.假設創建群聊時該部門除U0外共有n個在職員工U1,U2,…,Un，他們的身份標識符分別為ID1,ID2,…,IDn.由于每個員工的身份標識符與其賬號綁定，因此創建群聊時U0的客戶端會提交目前該部門所有在職員工的IDi(0 ≤i≤n)給服務器，然后服務器會為這個群聊創建一個唯一的群標識符group_ID，并返回group_ID和IDi(1 ≤i≤n)對應的Qi的值給U0，同時保存group_ID和群主U0的身份標識符ID0，這一過程如圖4 所示.在U0的客戶端按2.1.2 節分發密鑰之前，部門群處于禁言狀態，所有群成員在此時均不可發布聊天消息.

Fig.4 Department leader creates group chat圖4 部門領導創建群聊

接下來U0的客戶端先在本地隨機生成一個比特長度為len的整數q，然后隨機生成一個比特長度為len且滿足1 ≤K＜q的整數K，將K作為群組密鑰，按2.1.2 節所述的方式計算出C0,C1,…,Cn和an+2,an+1,…,a0.為了在公司的服務器上備份這些參數以供群內所有用戶恢復本地丟失的群組密鑰，U0的客戶端會1）先將(group_ID,compute_params,(ID0,C0),(ID1,C1),…,(IDn,Cn),an+2,an+1,…,a0,q)以某種格式封裝成報文，其中group_ID標識該報文來自于該部門群，compute_params用于表示該報文攜帶的是用于計算該部門群的群組密鑰的參數；2）將這條報文發送到服務器，由服務器將這條報文發送給其他群成員.群內的每個員工Ui收到這條報文之后對該報文進行解析，首先group_ID和compute_params理解該報文攜帶的數據的來源與含義，然后將自己的IDi依次與(ID0,C0),…,(IDn,Cn)進行比較，得到相應的Ci以及an+2,an+1,…,a0和q的值，最后按2.1.3 節中給出的3 個步驟計算出群組會話密鑰K；服務器在轉發這條報文的同時會對報文進行解析，提取并保存group_ID，(IDi,Ci)(0 ≤i≤n)，ai(0 ≤i≤n+2)和q.這一過程如圖5 所示.參數發送完畢之后，部門群解除禁言.

Fig.5 Group key distribution圖5 群組密鑰分發

在客戶端計算出群組密鑰K之后，Ui(1 ≤i≤n)即可在群里發送消息，消息經過K加密之后在局域網內傳輸.為了在公司的服務器上備份聊天記錄，部門群內的每個人在發送消息時，客戶端會將攜帶消息密文的報文發送給服務器，由服務器將報文轉發給群內的其他人，同時解析報文，提取并保存其中攜帶的數據.這一過程的一個具體示例如圖6 所示.

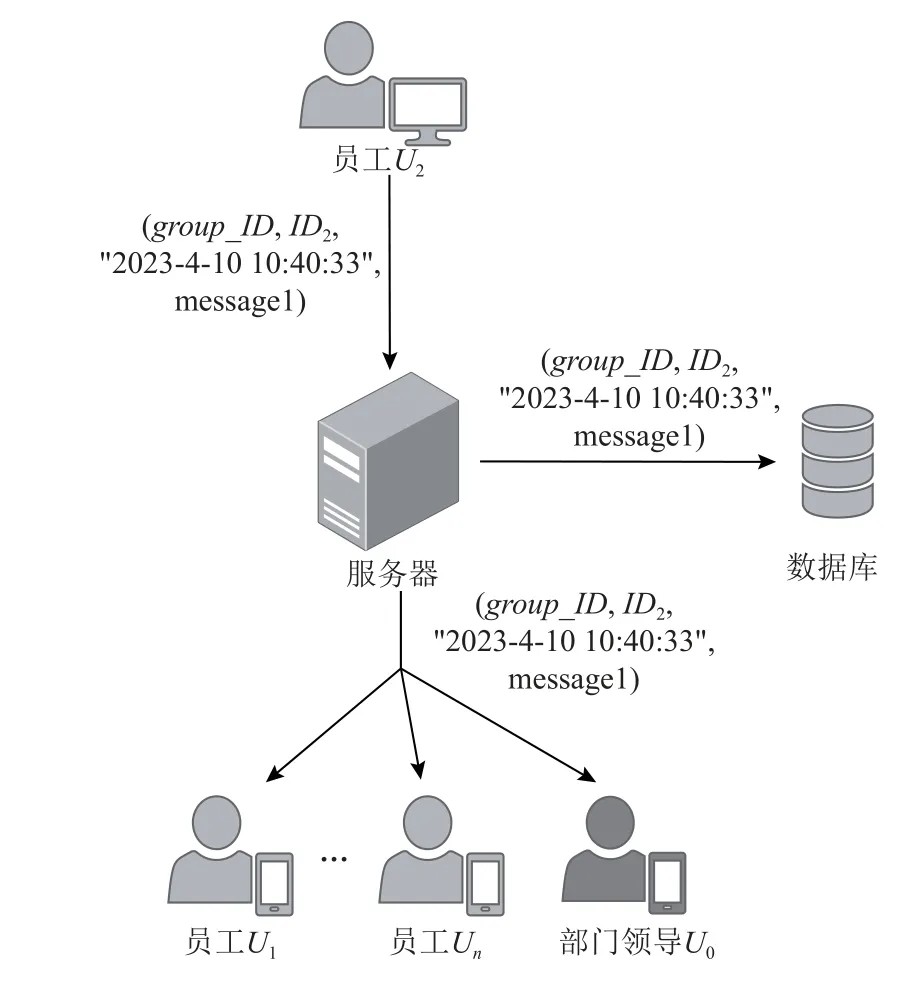
Fig.6 Group members send group chat messages圖6 群成員發送群聊消息

該部門群創建之后，新入職該部門的員工可選擇申請加入或被U0邀請加入群聊，新員工進群時，U0設置群為禁言狀態，然后U0的客戶端會重新生成一個群組密鑰，按照2.2 節所述的方式重新計算參數并按圖5 所示的方式發送參數，參數發送完畢之后，部門群解除禁言；若該部門有員工離職，則由U0強制將離職員工的賬號移出群聊，在此期間U0設置群為禁言狀態，然后U0的客戶端會重新生成一個群組密鑰，按照2.3 節所述的方式重新計算參數并按圖5 所示的方式發送參數，參數發送完畢之后，部門群解除禁言.

若該部門某員工Ui(0 ≤i≤n)的客戶端保存在本地的群組會話密鑰K丟失，他所使用的終端會向服務器發送查詢請求，服務器會返回用于計算K的相關參數給Ui的客戶端，這一過程如圖7 所示.

Fig.7 Group members query the server for the relevant parameters used to calculate the group key圖7 群成員向服務器查詢用于計算群組密鑰的相關參數

同理，當Ui存儲在本地的群聊天記錄丟失時，也可以向服務器發送查詢請求，獲得相關的聊天記錄密文后在本地解密即可.以Ui查詢身份標識符為ID2的用戶發送的全部群聊消息為例，如圖8 所示.

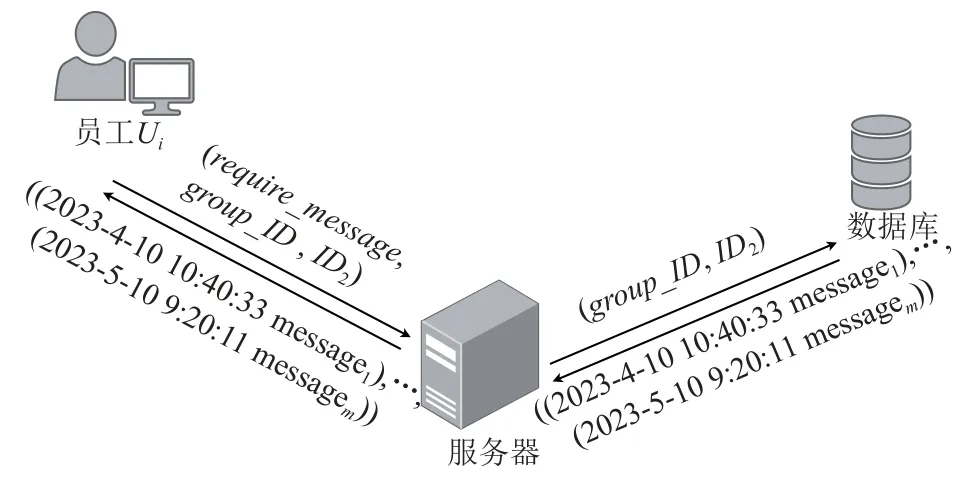
Fig.8 Group members query the server for group chat records圖8 群成員向服務器查詢群聊記錄

5.2 本文方案在點對點通信場景下的應用

本文方案還可以直接應用于點對點通信場景下作為一種端到端加密算法.本節將介紹本文方案是如何作為一種端到端加密算法來運行的.

在點對點通信場景下，參與通信的只有兩方.設參與通信的兩方為用戶U1和用戶U2，二者對應的公開參數與長期私鑰分別為(Q1,de1)和(Q2,de2)，以用戶U1向用戶U2發從一條消息為例.設用戶U1要發送的消息為M，U1首先隨機生成一個整數q，然后通過某種編碼方式將M編碼成一個與q比特長度相同且滿足1 ≤L＜q的整數L；接著U1生成2 個隨機數r1,r2∈[1,N-1]，并計算C1=[r1]Q1,C2=[r2]Q2和哈希值h1=H2(e([r1]Ppub-e,P2)),h2=H2(e([r2]Ppub-e,P2))，然后U1隨機選擇R∈[1,q-1]，構造多項式，并計算出各項的系數：

以上操作相當于對L進行加密.最后U1將C2,a3,a2,a1,a0和q發送給U2.U2在收到這些參數之后，首先驗證C2∈G1是否成立.若不成立則報錯并退出；若成立，U2首先計算哈希值h2=H2(e(C2,de2))，然后通過計算解密得到：

最后將L解編碼成消息M即可得到原始明文.

5.3 即時通訊軟件采用方案的對比

本節調研了目前市面上流行的一些即時通訊軟件加密群聊通信所使用的協議.由于許多主流的即時通訊軟件都沒有公布加密群聊消息所采用的協議的細節，因此本節只選取了Signal，WhatsApp 和Facebook Messenger 這3 款公布了群聊加密協議細節的即時通訊軟件進行分析.

Signal，WhatsApp 和Facebook Messenger 利用了端到端加密通訊協議Signal 來實現群聊消息加密[30-32]，Signal 協議實現群聊消息加密的大致流程如圖9所示[31-32].

Fig.9 Process of implementing group chat message encryption in Signal protocol圖9 Signal 協議中實現群聊消息加密的流程

假設群組內共有n+1名成員.由圖9 可知，為了得到加解密群聊消息的消息密鑰，Signal 協議中每個用戶需要首先產生1 個鏈密鑰和1 對簽名密鑰，再發送n條加密消息將鏈密鑰和簽名公鑰分別發送給群組中的其他用戶，并存儲由其余n個用戶發來的鏈密鑰和簽名公鑰，而且每次發送和接收消息時都需要從鏈密鑰中派生出消息密鑰并更新鏈密鑰，這些操作不僅會增加用戶客戶端的計算開銷和通信開銷，而且會加重客戶端的密鑰存儲和管理的負擔，因為每個客戶端都需要維護和管理大量的密鑰信息.

相比之下，本文方案流程更簡單，且能夠減輕客戶端在密鑰存儲和管理方面的負擔.為了更直觀地展示本文方案與Signal 協議中進行群聊加密所采取方法的差異，以及更好地評估本文方案的實用性，表6對比了本文方案和Signal 協議采取的方法.2 種方法都假設群內共有n+1個成員.

Table 6 Comparison Between Our Scheme and the Method Adopted by Signal Protocol表6 本文方案和Signal 協議采取的方法的對比

如表6 所示，與現有的方案對比之后，綜合而言，當應用于實際場景下時，本文方案具有5 點創新點和優勢：

1）本文方案采用了基于身份的密碼體制生成用戶的長期私鑰，相比于Signal 協議采取公鑰基礎設施（public key infrastructure,PKI）進行群組用戶的密鑰管理，本文方案消除了對公鑰證書的依賴，簡化了用戶密鑰的管理問題；

2）在群組密鑰管理上，相比于Signal 協議中實現群聊消息加密時需要存儲多個消息密鑰，本文方案中群組內每個用戶在本地客戶端只需存儲1 個用于加解密群聊消息的密鑰，只有群主更新群組密鑰時才需要增加存儲新的群組密鑰，降低了存儲開銷，減輕了客戶端管理群組密鑰的負擔；

3）在通信開銷上，相比于Signal 協議中實現群聊消息加密時每個用戶在通信開始前要向群內其他所有用戶單獨發送消息，本文方案在群組密鑰分發階段只有群主需要向其他群成員廣播1 次參數，而每個普通群成員則不需要與其他群成員進行交互，降低了通信開銷；

4）應用于實際場景時，本文方案可以做到在客戶端不存儲參數的情況下恢復丟失的群組密鑰.如圖7 所示，當群成員客戶端存儲的群組密鑰丟失時，可以向服務器發送參數請求報文，獲取存儲在服務器端的參數之后在本地重新計算出群組密鑰.

5）本文方案在n=2 時可直接用于點對點通信場景下的端到端加密.

6 總結與展望

本文基于國密SM9 算法提出了一種應用于即時通訊群聊場景下的基于身份的群組密鑰分發方案，并給出了嚴格的安全性證明；同時，對所提出的方案進行了存儲開銷、通信開銷的理論分析，并對時間開銷進行了仿真實驗分析.將本文方案與文獻[17-18]的方案進行了對比，發現本文方案在便捷性和兼容性上更具有優勢；并與文獻[13]提出的ASGKA 方案進行了對比，發現本文方案在密鑰管理和兼容性上更具有優勢.本文方案可以應用于即時通訊軟件的群聊加密場景，在這一場景下本文方案相比于已應用于商業軟件的方案而言具有一定的創新性和優勢，同時本文方案可以直接用于點對點通信場景下的端到端加密.未來的工作可圍繞進一步提升方案的安全性和計算效率這兩方面展開.

作者貢獻聲明：王后珍提出了算法思路和實驗方案；秦婉穎負責完成實驗并撰寫論文；劉芹、余純武、沈志東提出了實驗方案的優化與改進.