低跨云數據中心修復流量的糾刪碼的快速構造方法

包 涵 王意潔

（并行與分布計算全國重點實驗室（國防科技大學） 長沙 410073）

（國防科技大學計算機學院 長沙 410073）

近年來，云數據中心故障頻發，常導致其中數據長時間不可訪問[1-6].同時，云際計算技術的逐漸成熟使得部署跨云數據中心存儲系統更加便捷[7].因此，各機構紛紛采用跨云數據中心多副本技術來實現重要數據的容災存儲[8].

相較于跨云數據中心多副本技術，跨云數據中心糾刪碼技術具有更高的可靠性和更低的冗余度[9-12].然而，跨云數據中心糾刪碼技術要在生產系統中得到普遍運用，還需滿足3 方面要求：

1）低跨云數據中心修復流量.糾刪碼技術在跨云數據中心存儲系統中修復故障節點中的數據時，需跨云數據中心傳輸大量數據，即糾刪碼技術的跨云數據中心修復流量較大.由于云數據中心間帶寬往往遠低于云數據中心內帶寬，所以糾刪碼技術在跨云數據中心存儲系統中修復數據的時間較長[13-15].因此，亟需降低糾刪碼的跨云數據中心修復流量.

2）高編碼參數適應性.在生產中，用戶通常對存儲節點數n、冗余度n/k、容錯度d和容災度D等糾刪碼編碼參數具有多樣化需求.因此，有必要提高跨云數據中心糾刪碼的編碼參數適應性.編碼參數為（n,k,d,D）的糾刪碼將每k個數據塊編碼為n個編碼塊，并將其分別存儲在位于多個云數據中心的n個存儲節點，且當任意d-1個存儲節點或任意D個云數據中心故障時，其中存儲的編碼塊可由其他編碼塊修復.

3）高糾刪碼構造效率.因為糾刪碼編解碼數據的過程與存儲系統的讀寫過程深度耦合，所以開發和部署存儲系統前需先完成糾刪碼的構造，因而用戶通常對糾刪碼構造用時較為敏感.因此，有必要提高跨云數據中心糾刪碼的構造效率.

現有工作提出的跨云數據中心糾刪碼[13-18]雖然能在一定程度上降低跨云數據中心修復流量，但普遍存在編碼參數適應性較低的問題，無法在滿足用戶對編碼參數的多樣化需求的同時有效降低跨云數據中心修復流量.此外，有工作提出了面向跨云數據中心存儲的自適應糾刪碼ACIoT[19]，可求得不同編碼參數（n,k,d）下的跨云數據中心修復流量下限，并構造能達到該下限的糾刪碼，即最優碼.但是，ACIoT需要消耗較長時間來檢驗糾刪碼修復組分布方案與編碼參數（n,k,d）的匹配性，故其糾刪碼構造效率較低.糾刪碼修復組分布方案E與指定編碼參數P相匹配是指存在一個編碼參數為P的糾刪碼的修復組分布方案為E.

綜上，現有工作無法兼顧編碼參數適應性、糾刪碼跨云數據中心修復流量和糾刪碼構造效率.本文提出一種低跨云數據中心修復流量的糾刪碼的快速構造方法（fast construction method of the erasure code with small cross-cloud data center repair traffic）FMEL，可在不同的編碼參數下快速構造出具有較低跨云數據中心修復流量的糾刪碼.FMEL 的主要思想為：

首先，FMEL 將糾刪碼修復組分布方案及相應的編碼參數（n,k,d,D）轉換為定長特征向量，并將檢驗糾刪碼修復組分布方案與指定編碼參數匹配性的問題轉換為定長特征向量的二分類問題.其中，特征向量屬于正類表示糾刪碼修復組分布方案與相應編碼參數相匹配.然后，FMEL 采用具有較高分類效率的支持向量機（support vector machine,SVM）來對各個特征向量進行分類以實現其所對應糾刪碼修復組分布方案的快速檢驗.在檢驗的同時，FMEL 不斷采集新的訓練集對SVM 分類器進行增量更新，從而不斷提高其分類準確率.隨后，FMEL 采用一種并行搜索方法來快速地從所有可通過SVM 檢驗的糾刪碼修復組分布方案中選出跨云數據中心修復流量最小的一個方案.最后，FMEL 采用一種基于試錯的糾刪碼修復組分布方案轉換方法將搜索到的糾刪碼修復組分布方案轉換為具有低跨云數據中心修復流量的糾刪碼的生成矩陣.

在跨云數據中心環境中的實驗表明，FMEL 在大部分編碼參數下可構造出能達到平均跨云數據中心修復流量下限的最優碼，且其構造糾刪碼的時間僅為現有工作構造最優碼時間的11%.

1 相關工作

1.1 單云數據中心糾刪碼

現有工作提出了2 類低修復流量糾刪碼——再生碼和局部性碼.再生碼通過降低新生節點從各提供者節點里的編碼塊中讀取的數據量來減少修復流量，局部性碼通過降低各個編碼塊的提供者節點數量來減少修復流量.與再生碼相比，局部性碼更容易實現且靈活性更高，因而被廣泛地應用于Amazon AWS[20]，Microsoft WAS[21]，Facebook HDFS-RAID[22]等生產系統中.特別地，Shahabinejad 等人[23]提出了一種可達到平均修復流量下限的糾刪碼ACAL.

雖然現有單云數據中心糾刪碼能夠降低平均修復流量，但是跨云數據中心修復流量并不與修復流量正相關.因此，這些糾刪碼在跨云數據中心環境下不能充分降低跨云數據中心修復流量.

1.2 跨云數據中心糾刪碼

Yu 等人[13]提出了一種跨域容錯糾刪碼DFC，其基本思想是在傳統的RS 碼的基礎上引入局部校驗塊，首先使用RS 碼將k個數據塊編碼為w個編碼塊并在N個云數據中心中各存儲w/N(w/N≤w-k)個數據塊.由于RS 碼可以保證在這w個編碼塊中的任意w-k個編碼塊失效時重構原始數據，所以在任意一個云數據中心故障時，仍可以通過其他云數據中心里的w-w/N(w-w/N≥k)個編碼塊恢復出原始數據.然后，DFC 為每個機架存放的編碼塊生成局部校驗塊，使得在任意一個編碼塊失效時，可以使用機架內的編碼塊和局部校驗塊對其進行修復.因此，DFC 的跨云數據中心修復流量較小.但是，DFC 對編碼參數具有嚴格的限制，要求n-k-d+1≥N.

Caneleo 等人[14]提出了一種多倍異或碼MXOR，其基本思想是將數據塊分為2 行k/2 列，而后通過異或計算分別求得各行各列的局部校驗塊，然后將所有編碼塊和局部校驗塊按行分散到各云數據中心.當單個編碼塊失效時，MXOR 可通過對云數據中心內部的其他編碼塊和局部校驗塊進行異或計算對其進行修復，因此MXOR 的跨云數據中心修復流量較小.但是，MXOR 對編碼參數具有嚴格的限制，要求n/k≥2.4且d≤4.

Chen 等人[15-16]和Hu 等人[17]分別提出FMSR 碼和DRC 碼均能有效降低跨云數據中心修復流量.然而，FMSR 和DRC 均對編碼參數有嚴格的限制，FMSR 要求n-k=2，而DRC 碼要求n,k,N（云數據中心數）至少滿足2 個條件中的1 個：1）n=3z,k=2z,N=3（z為正整數）；2）N=n/（n-k）.

雖然上述糾刪碼均能在一定程度上降低跨云數據中心修復流量，但它們普遍存在編碼參數適應性較差的問題，無法在滿足用戶對編碼參數的多樣化需求的同時有效降低跨云數據中心修復流量.為此，有工作[19]提出了面向跨云數據中心存儲的自適應糾刪碼ACIoT，可求得不同編碼參數（n,k,d）下的最小跨云數據中心修復流量碼，即最優碼.具體而言，ACIoT 首先定義了糾刪碼的修復組分布方案，該方案決定了糾刪碼的跨云數據中心修復流量.然后，ACIoT可枚舉指定編碼參數（n,k）下的糾刪碼修復組分布方案，并檢驗它們是否與指定編碼參數（n,k,d）相匹配.最后，ACIoT 可從所有與編碼參數（n,k,d）相匹配的糾刪碼修復組分布方案中找出具有最小跨云數據中心修復流量的1 個并將其轉換為最優碼生成矩陣.然而，ACIoT 忽略了容災度對跨云數據中心修復流量下限的影響.此外，因ACIoT 需要消耗較長時間來檢驗糾刪碼修復組分布方案與編碼參數（n,k,d）的匹配性，故其糾刪碼構造用時較長.

綜上，現有的跨云數據中心糾刪碼無法同時滿足低跨云數據中心修復流量、高編碼參數適應性和高糾刪碼構造效率，這嚴重限制了其在生產系統中的運用.

除以上聚焦于數據修復的工作外，Saeed 等人[24]還考慮到RS 碼等糾刪碼技術在讀取數據時具備多種讀取方案，可以通過訪問不同云數據中心的節點來重構用戶數據.因此，他們提出了距離優先讀取策略和負載均衡優先讀取策略，分別用于對讀取過程的網絡開銷和各存儲節點的負載進行優化.同時，他們對用戶讀取數據時的網絡開銷和各節點的負載進行了綜合建模，得到了一個綜合考慮2 方面因素的開銷模型，并基于此模型提出了跨數據中心糾刪碼數據讀取節點選擇算法Sandooq，能夠有效降低數據讀取的綜合開銷.此外，我們在之前的工作中提出了一種跨云數據中心糾刪碼增量寫入方法[25]和一種基于生成矩陣變換的跨云數據中心糾刪碼寫入方法[26]，可分別通過提高編碼并行度和降低跨云數據中心寫入流量來提高寫入效率.

2 重要定義及定理

定義1.生成矩陣.跨云數據中心糾刪碼技術將用戶數據劃分為若干數據塊，并將每k個數據塊（記為xt,t∈[1,k]）編碼為n個編碼塊（記為yi,i∈[1,n]），這n個編碼塊被稱為一個條帶，編碼過程如式（1）所示，其中G為糾刪碼的生成矩陣.生成矩陣G的秩必須為k,否則GT(z1,…,zk)T=(y1,…,yn)T沒有唯一解，即無法將一個條帶中的n個編碼塊解碼為原始數據塊.

定義 2.校驗矩陣. 如果為G[z1,…,zk]T=0的基礎解系，那么H=為對應于生成矩陣G的校驗矩陣.因為G的秩為k，所以H的秩為n-k.

定義3.修復組.由生成矩陣G與校驗矩陣H的定義有，GHT=0，故(y1,…,yn)HT=(x1,…,xk)GHT=0.因此，每個編碼塊都可以通過對其他若干個編碼塊進行線性計算重構.如果編碼塊yi可以通過對yi,1,yi,2,…,yi,r進行線性計算重構，那么{yi,yi,1,yi,2,…,yi,r}為yi的一個修復組（用于修復yi的存儲節點被稱為新生節點，存儲yi,1,yi,2…,yi,r的節點被稱為提供者節點）.一個編碼塊可能有多個修復組.此外，由于編碼塊之間的線性關系由生成矩陣G或校驗矩陣H決定，所以編碼塊的修復組也是由生成矩陣G或校驗矩陣H決定的.

定義4.編碼塊分布方案.一個條帶中的編碼塊所在的云數據中心的編號組成的集合為該條帶的編碼塊分布方案R={z1,z2,…,zn}，其中zi表示該條帶中第i個編碼塊位于第zi個云數據中心.

定義5.編碼塊修復組分布方案.設Ti,w為編碼塊yi的第w個修復組，如果Ti,w中的編碼塊分布于t個編號分別為z1,z2,…,zt的云數據中心中（這t個云數據中心分別記為，那么令Ri,w={z1,z2,…,zt}.設編碼塊yi共有Qi個修復組，記為Ti,1,Ti,2,…,Ti,Qi，且（q∈[1,Qi]），那么Ri,q為編碼塊yi的修復組分布方案.其中，表示Ri,w中含有的云數據中心編號個數.

定義6.糾刪碼修復組分布方案.如果C1,C2,…,Cn分別為編碼塊y1,y2,…,yn的修復組分布方案，那么{C1,C2,…,Cn}為條帶{y1,y2,…,yn}的修復組分布方案.通常而言，糾刪碼的不同編碼條帶中的編碼塊在各個云數據中心間的分布相同.在此情況下，糾刪碼的各個條帶的修復組分布方案相同，因而條帶的修復組分布方案也被稱為糾刪碼修復組分布方案.

為了降低跨云數據中心修復流量，在基于糾刪碼技術的跨云數據中心存儲系統修復編碼塊時，含有提供者節點的云數據中心通常會先將其中的提供者節點的編碼塊合并為一個和各個編碼塊大小相同中間塊，然后再將中間塊發往新生節點.此外，為了保持系統的容災度和負載均衡性不變，失效編碼塊的新生節點通常和該失效編碼塊位于同一云數據中心.在此情況下，如果編碼塊yi的修復組分布方案為Ci且編碼塊大小為m，那么在修復yi時需要向其新生節點發送中間塊的云數據中心（含新生節點所在云數據中心）的個數為Ci中含有的云數據中心編號個數 |Ci|，因而修復yi的最小跨云數據中心傳輸量為m（|Ci|-1）.所以，一個糾刪碼的修復組分布方案為E的糾刪碼的編碼條帶的平均跨云數據中心流量為其中，C為E中的編碼塊修復組分布方案，n為一個編碼條帶中的編碼塊數.因此，糾刪碼的平均跨云數據中心修復流量由其修復組分布方案決定.

定義7.糾刪碼Tanner 圖[23].若一個編碼參數為（n,k,d,D）的糾刪碼CO的校驗矩陣為H，那么該糾刪碼的Tanner 圖 T 為滿足3 個條件的二分圖：1) T的一個端點集包含n個變量端點（variable node,VN）；2)T的另一個端點集包含n-k個校驗端點（check node,CN）；3）當且僅當H的第i行、第j列的元素不為0，T的第j個校驗端點覆蓋其第i個變量端點，即 T中有一條以第j個校驗端點和第i個變量端點為端點的邊.圖1 舉例說明了糾刪碼的Tanner 圖與糾刪碼校驗矩陣H間的關系.

Fig.1 Erasure code’s Tanner graph圖1 糾刪碼Tanner 圖

圖2 舉例說明了糾刪碼Tanner 圖與編碼塊和修復組之間的關系.糾刪碼的一個編碼條帶中的6 個編碼塊y1,y2,…,y6分別對應著該糾刪碼Tanner 圖的6 個變量端點VN1,VN2,…,VN6.覆蓋糾刪碼Tanner 圖中的第1,4,5,6 個變量端點VN1,VN4,VN5,VN6的校驗端點CN1對應的修復組為{y1,y4,y5,y6}，該修復組內各編碼塊之間的線性關系為y1+y4+y5+y6=0.同理，校驗端點CN2對應的修復組為{y2,y4,y5,y6}，該修復組內各編碼塊的線性關系為y2+y4+2y5+4y6=0；校驗端點CN3對應的修復組為{y3,y4,y5,y6}，該修復組內各編碼塊的線性關系為y3+y4+3y5+9y6=0.

Fig.2 The relationship between the erasure code’s Tanner graph,coded blocks,and the repair groups圖2 糾刪碼Tanner 圖與編碼塊和修復組之間的關系

本文涉及的常用符號及其含義如表1 所示：

定理2.假設H(n-k)×n為糾刪碼CO的校驗矩陣.當且僅當由H的第z1～zc列組成的矩陣H1的秩為c，CO能夠在其各條帶中的第l1～lc個編碼塊同時失效時修復這些失效編碼塊.

證明.從糾刪碼的校驗方程(y1,…,yn)HT=0中得到的以為未知數的方程組如式（2）所示：

因為式（2）中的最大線性無關方程數等于H1的秩，所以，當且僅當H1的秩為c時，式（2）有唯一解.因此，當且僅當H1的秩為c時，能夠被同條帶中的其他編碼塊修復.證畢.

定理3.假設糾刪碼的編碼塊分布方案R已確定，即任意條帶中的n個編碼塊被分配給N個云數據中心，亦即糾刪碼Tanner 圖 T的n個變量端點和相應的校驗矩陣H的n個列被分配給了N個云數據中心（根據定義7，糾刪碼Tanner 圖 T的n個變量端點分別對應于校驗矩陣H的n個列和任意條帶中的n個編碼塊）.在此假設下，T 匹配于編碼參數（n,k,d,D）的一個充要條件是：T有n-k個校驗端點、n個變量端點（子條件1）；T的任意 γ個校驗端點至少覆蓋γ+k個變量端點，其中，γ ∈[J,n-k]且J=n-k-d+2（子條件2）；T的最大匹配數不小于n-k（子條件3）；任意含有B(B≤n-k)個變量端點的D個云數據中心中的任意β(β∈[1,B])個變量端點至少覆蓋個校驗端點（子條件4）.

證明.1）必要性證明.

①子條件1 的必要性.

根據定義7，若 T匹配于編碼參數（n,k,d,D），那么其對應的糾刪碼的生成矩陣一定有k行n列.根據糾刪碼Tanner 圖與糾刪碼的生成矩陣的關系，T一定有n-k個校驗端點、n個變量端點，即 T一定滿足子條件1.

② 子條件2 的必要性.

如果在 T中存在 γ個校驗端點（不妨設為CN1,CN2,…,CNγ）僅覆蓋了w個變量端點（不妨設為VN1,VN2,…,VNw）且w≤γ+k-1，那么根據定義7，對應于T的校驗矩陣如式（3）所示.其中，0γ×(n-w)為全零矩陣.

（i）如果n-w≤d-1，從糾刪碼的校驗方程(y1,…,yn)HT=0中只能得到以yw+1,yw+2,…,yn為未知數的線性方程組：

因為n-w≤d-1，所以n-w≥n-(γ+k-1)=n-kγ+1.所以，式（4）中的具有n-w個未知數和n-k-γ個方程的方程組無唯一解.因此，yw+1,yw+2,…,yn不能由同條帶中的其他編碼塊修復.因此，T不匹配于編碼參數d.

（ii）如果n-w＞d-1，從糾刪碼的校驗方程[y1,…,yn]HT=0中只能得到以yn-d+2,yn-d+3,…,yn為未知數的線性方程組：

因為γ∈[J,n-k]且J=n-k-d+2，所以n-k-γ≤nk-(n-k-d+2)=d-2.所以，式（5）中的具有d-1個未知數和n-k-γ個方程的方程組無唯一解.因此，yn-d+2,yn-d+3,…,yn不能由同條帶的其他編碼塊修復.因此，T不匹配于編碼參數d.

綜上，如果 T匹配于編碼參數（n,k,d,D），T的任意 γ個校驗端點至少覆蓋γ+k個變量端點，其中γ∈[J,n-k]且J=n-k-d+2.

③子條件3 的必要性證明.

假設 T的最大匹配數為b＜n-k且H(含有n-k行、n列）為任意一個對應于 T的校驗矩陣，那么由定理1 有，H的每個n-k行、n-k列的子矩陣均不滿秩.因此，H的秩不為n-k.因此，根據校驗矩陣的定義，H不可能是一個（n,k,d,D）糾刪碼的校驗矩陣.因此，T不匹配于（n,k,d,D）.因此，若 T匹配于編碼參數（n,k,d,D），T 的最大匹配數不小于n-k.

④ 子條件4 的必要性證明.

如果存在D個云數據中心（不妨設為），其中的 β個變量端點（不妨設為VN1,VN2,…,VNβ)只覆蓋了c≤β-1個校驗端點（不妨設為CN1,CN2,…,CNc)，那么根據定義7，對應于 T的校驗矩陣H中只有c個行中的第1～ β列中存在非零元素.因此，從糾刪碼的校驗方程(y1,…,yn)HT=0中只能得到以y1,y2,…,yβ為變量的線性方程組:

因為式（6）中的 β元方程組的最大線性無關方程數為c(c＜β)，所以該方程組沒有唯一解.因此，對應于 T 的糾刪碼的任意編碼條帶{y1,y2,…,yn}中的y1,y2,…,yβ不能被同條帶的其他編碼塊修復 (T對應的糾刪碼不能容忍同時失效）.因此，T不匹配于編碼參數（n,k,d,D）.

綜上，若 T匹配于編碼參數（n,k,d,D），任意含有B(B≤n-k)個變量端點的D個云數據中心中的任意β(β∈[1,B])個變量端點至少覆蓋 β個校驗端點.

2）充分性證明.

證明.假設糾刪碼Tanner 圖 T 符合定理3 中的充要條件，那么可按5 個步驟構造出一個糾刪碼Tanner 圖為 T的匹配于編碼參數（n,k,d,D）的糾刪碼的生成矩陣，即 T匹配于編碼參數（n,k,d,D）.

①求得 T 的最大匹配.因為 T 滿足定理3 中的充要條件的子條件3，所以其最大匹配包含n-k個變量端點.如果 T 的最大匹配包含，那么令H1為由H的第l1,l2,…,ln-k列組成的矩陣.由于H1的行數和列數均為n-k，所以其為方陣.然后，我們將H1加入集合LS.

② 求得H的所有的包含n-k行、d-1 列的子矩陣的集合SM1以及H的所有的包含其對應于任意D個云數據中心的列的子矩陣組成的集合SM2.

③根據糾刪碼Tanner 圖的定義，SM1和SM2中每個矩陣都對應于 T的一個子圖.因此，我們求得對應于SM1和SM2中每個矩陣所對應的 T的子圖的最大匹配.而后，對于SM1和SM2中的每個矩陣Z，如果其對應的 T的子圖的最大匹配包含則將其第l1,l2,…,lc行組成的子矩陣加入集合LS.

可以證明，如果SM1或SM2中的某個矩陣有q列，那么其對應的 T的子圖的最大匹配一定為q（即LS中的矩陣均為方陣），證明過程為：

首先，證明如果SM1中的某個矩陣有q列，那么它的最大匹配數一定為q.由于SM1的矩陣的列數恒為d-1，因此只需要證明SM1中的矩陣對應的 T的子圖的最大匹配數恒為d-1.

（i）令?=n-k-γ+1(因為γ∈[J,n-k]且J=n-kd+2，所以?∈[1,d-1])，可以證明 T中任意 ?個變量端點至少覆蓋 ?個校驗端點：如果存在 ?個變量端點僅僅覆蓋u≤?-1個校驗端點，那么剩下的n-k-u≥γ個校驗端點最多覆蓋n-?=k+γ-1個變量端點，這與定理3 中的充要條件的子條件2（任意 γ個校驗端點至少覆蓋γ+k個變量端點）相矛盾.因此，任意 ?個變量端點至少覆蓋 ?個校驗端點.

（ii）根據Hall 定理[27]，在 T 的任意含有d-1 個變量端點、n-k個校驗端點（d-1＜n-k）的子圖存在完全匹配的充要條件是該子圖中任意 ?個變量端點至少覆蓋 ?個校驗端點（?∈[1,d-1]）.由（i）有，T中任意?個變量端點至少覆蓋 ?個校驗，所以 T的任意含有d-1 個變量端點、n-k個校驗端點（d-1＜n-k）的子圖存在完全匹配，即 T中任意d-1 個變量端點可以一對一地覆蓋d-1 個校驗端點.

（iii）假設Z為SM1中的任意矩陣且Z包含H的第l1,l2,…,ld-1列.由（ii）有，一定一對一地覆蓋d-1個校驗端點（不妨設為CN1,CN2,…,CNd-1).因此，為對應于Z的 T的子圖的最大匹配.因此SM1中任意矩陣對應的 T的子圖的最大匹配數為d-1.

然后，證明如果SM2中的某個矩陣有B列，那么它的最大匹配數一定為B.

（i）不妨假設 T中對應于任意D個云數據中心的任意B個變量端點為VN1,VN2,…,VNB.根據Hall 定理[27]，T的由其VN1,VN2,…,VNB和n-k個校驗端點組成的子圖存在完全匹配的充要條件是該子圖中任意β個變量端點至少覆蓋 β個校驗端點（β∈[1,B]）.因為T滿足定理3 中的充要條件的子條件4，即任意含有B(B≤nk)個變量端點的D個云數據中心中的任意β(β∈[1,B])個變量端點至少覆蓋 β個校驗端點，所以T的由其VN1,…,VNB和n-k個校驗端點組成的子圖存在完全匹配，即 T中對應于任意D個云數據中心的任意B個變量端點一定可以一對一地覆蓋B個校驗端點.

定理4.糾刪碼修復組分布方案E匹配于編碼參數（n,k,d,D）的一個必要條件為：設ST為E中所有編碼塊修復組分布方案的無重復集合，對于任意D個共含有B個編碼塊的云數據中心（不妨設這些云數據中心的編號為z1,z2,…,zD，即設這些云數據中心為），ST中僅含有不多于n-k-B個不包含這些云數據中心的編號集合{z1,z2,…,zD}中任意元素的編碼塊修復組分布方案.

證明.根據定義6，如果ST中含有超過n-k-B個不包含{z1,z2,…,zD}中任意元素的編碼塊修復組分布方案，那么相應的糾刪碼有超過n-k-B個不含有中編碼塊的修復組.因此，根據定義7，在任何對應于E的糾刪碼Tanner 圖（不妨設為T)中，一定有超過n-k-B個校驗端點沒有覆蓋對應于中編碼塊的變量端點.因此，在T中，對應于中編碼塊的變量端點（不妨設為)覆蓋的校驗端點少于B個.因此，根據定義7，任意對應于 T的校驗矩陣H中的第l1,l2,…,lB列組成的矩陣H1最多只有B-1 個非零行.因此，H1的秩小于B.因此，根據定理2，校驗矩陣為H的糾刪碼不能容忍任意編碼條帶中的第l1,l2,…,lB個編碼塊失效，即不能容忍同時失效.因此，糾刪碼修復組分布方案E不匹配于編碼參數（n,k,d,D）.證畢.

定理5.所有匹配于指定編碼參數（n,k,d,D）的糾刪碼修復組分布方案的平均跨數據中心修復流量的最小值為編碼參數（n,k,d,D）下的糾刪碼的平均跨數據中心修復流量下限.

證明.令所有匹配于指定編碼參數（n,k,d,D）的糾刪碼修復組分布方案的平均跨數據中心修復流量的最小值為T.假設存在一個滿足編碼參數（n,k,d,D）且平均跨數據中心修復流量小于T的糾刪碼（不妨設為CO），那么CO的修復組分布方案的平均跨數據中心修復流量小于T.因為所有匹配于指定編碼參數（n,k,d,D）的糾刪碼修復組分布方案的平均跨數據中心修復流量的最小值為T，所以不匹配于編碼參數（n,k,d,D），因而不存在一個滿足編碼參數（n,k,d,D）的糾刪碼的修復組分布方案為，這與CO的修復組分布方案為相矛盾.因此，不存在一個匹配于編碼參數（n,k,d,D）且平均跨數據中心修復流量小于T的糾刪碼，即T為編碼參數（n,k,d,D）下的糾刪碼的平均跨數據中心修復流量下限.證畢.

3 低跨云數據中心修復流量的糾刪碼的快速構造方法FMEL

本節提出了一種低跨云數據中心修復流量的糾刪碼的快速構造方法FMEL（如圖3 所示），可在不同編碼參數下快速求得具有低跨云數據中心修復流量的糾刪碼.

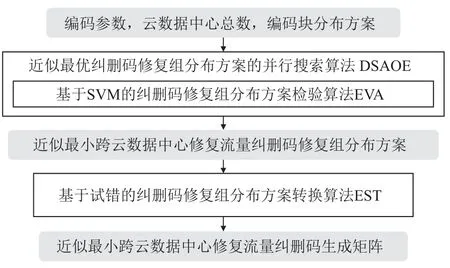
Fig.3 The structure of FMEL圖3 FMEL 的結構

具體而言，基于第2 節推導出的相關定理，本節首先得出糾刪碼修復組分布方案匹配指定編碼參數（n,k,d,D）的條件，并以此為依據提出了一種基于SVM 的糾刪碼修復組分布方案檢驗算法（erasure code repair group distribution scheme verification algorithm based on SVM）EVA，可對糾刪碼修復組分布方案與編碼參數匹配性進行快速檢驗.

然后，本節提出了一種具有近似最小跨云數據中心修復流量的糾刪碼修復組分布方案的并行搜索算法（distributed search algorithm of the erasure code repair group distribution scheme with the approximate minimum cross-cloud data center repair traffic）DSAOE，可從所有通過EVA 檢驗的糾刪碼修復組分布方案中選出平均跨云數據中心修復流量較小的一個糾刪碼修復組分布方案.

最后，本節提出一種糾刪碼修復組分布方案轉換算法（erasure code repair group distribution scheme transformation algorithm）EST，可將DSAOE 搜索到的修復組分布方案轉換為具有低跨云數據中心修復流量的糾刪碼的生成矩陣.

3.1 糾刪碼修復組分布方案匹配于指定（n,k,d,D）的條件

1）糾刪碼修復組分布方案匹配于指定（n,k,d,D）的充要條件

糾刪碼修復組分布方案是由糾刪碼的編碼塊的修復組和位置決定.如果將一個糾刪碼Tanner 圖的各個變量端點分配給不同的云數據中心，那么糾刪碼Tanner 圖可以同時反映相應糾刪碼的編碼塊的修復組及位置.因此，每個糾刪碼Tanner 圖對應一個糾刪碼修復組分布方案.因為多個糾刪碼Tanner 圖可能對應同一個糾刪碼修復組分布方案，所以每個糾刪碼修復組分布方案通常對應多個糾刪碼Tanner 圖.糾刪碼Tanner 圖 T匹配于編碼參數（n,k,d,D）是指存在一個Tanner 圖為 T的糾刪碼的編碼參數為（n,k,d,D）.因此，若一個糾刪碼修復組分布方案所對應的糾刪碼Tanner 圖中，有不少于一個糾刪碼Tanner 圖匹配于編碼參數（n,k,d,D），則該方案匹配于編碼參數（n,k,d,D），反之則該方案不匹配于編碼參數（n,k,d,D）.即糾刪碼修復組分布方案匹配于編碼參數（n,k,d,D）的充要條件是至少存在一個與之對應的Tanner 圖滿足定理3 中的子條件1～4.

2）糾刪碼修復組分布方案匹配于指定（n,k,d,D）的必要條件

糾刪碼修復組分布方案匹配于編碼參數（n,k,d,D）的一個必要條件如定理4 所示.

3.2 EVA 算法

基于3.1 節得出的糾刪碼修復組分布方案匹配指定編碼參數（n,k,d,D）的條件，首先，EVA 把糾刪碼修復組分布方案和對應的編碼參數轉換為便于分類算法高效處理的定長特征向量，轉換過程能夠保留判斷糾刪碼修復組分布方案是否匹配于指定編碼參數所需的全部信息，因而能夠保證分類的準確性.此外，EVA 使用一個SVM 來對定長特征向量進行分類以達到快速檢驗糾刪碼修復組分布方案是否匹配于對應的編碼參數的目的.在分類過程中，EVA 可以持續收集更多帶標簽定長特征向量，并使用這些定長特征向量對SVM 分類器進行增量更新，從而達到不斷提高分類準確率的目的.EVA 使用3.1 節推導出的糾刪碼修復組分布方案匹配于指定編碼參數（n,k,d,D）的條件為定長特征向量打標簽，以得到SVM 分類器的初始訓練數據集和增量更新數據集.

3.2.1 特征向量構造

基于SVM 的EVA 對糾刪碼修復組分布方案進行轉換：

首先，由定義6 有，如果可用云數據中心的數目為N，那么編碼塊的修復組分布方案C一共有2N-1個可能的取值.因此，EVA 將把這 2N-1個可能的取值一一映射為1,2,…,2N-1，映射函數如式（9）所示.

然后，對于每個云數據中心，EVA 將統計出糾刪碼修復組分布方案中對應于該云數據中心中的編碼塊的修復組分布方案的映射值中1,2,…,2N-1出現的次數，從而得到了一個長度為N(2N-1)的定長特征向量X'，該向量中的第a×b個元素的值為c表示第a個云數據中心中有c個編碼塊的修復組分布方案的映射值為b.例如，如圖4 所示，如果糾刪碼修復組分布方案為{{1},{1,2},{1,2},{2,3},{1,2,3},{1,2,3}}、云數據中心總數為3、編碼條帶中的第1,2 個編碼塊位于第1個云數據中心、編碼條帶中的第3,4 個編碼塊位于第2 個云數據中心、編碼條帶中的第5,6 個編碼塊位于第3 個云數據中心，那么其中各個編碼塊修復組分布方案的映射值分別為1,3,3,6,7,7，因而相應的X'=(1,0,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,2).

因為X'中含有各個云數據中心中的對應于不同修復組分布方案的編碼塊數目，所以使用X'可以恢復出各個云數據中心中的編碼塊的修復組分布方案的無序集合.例如，從X'=(1,0,1,0,0,0,0,0,0,1,0,0,1,0,0,0,0,0,0,0,2)的第3× 7 個元素為2 可以推導出第3 個云數據中心中有2 個編碼塊的修復組分布方案的映射值為7，即它們的修復組分布方案為{1,2,3}.因此，和原始的糾刪碼修復組分布方案相比，X'中僅僅丟失了各個編碼塊在各云數據中心內的順序信息.因為各個編碼塊在各云數據中心內的順序并不影響糾刪碼的冗余度、容錯度和容災度，因此糾刪碼修復組分布方案轉換過程沒有丟失判斷一個其是否匹配于編碼參數（n,k,d,D）所需的有效信息.

在將糾刪碼修復組分布方案轉換為一個數值型的定長特征向量X'后，EVA 將n,k,d,D追加到X'即可得到用于表示糾刪碼修復組分布方案及其對應編碼參數（n,k,d,D）的特征向量X，其長度恒為N(2N-1)+4.

3.2.2 基于SVM 的特征向量分類

由于匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案之間以及不匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案之間均有一定的相似性，所以匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案對應的特征向量之間以及不匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案對應的特征向量之間存在一定的相似性.因此，可以采用有監督學習算法[28-29]來對糾刪碼修復組分布方案對應的特征向量進行分類：使用一些已知匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案對應的特征向量和已知不匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案對應的特征向量作為訓練集來訓練一個分類器.分類器會判斷新的糾刪碼修復組分布方案對應的特征向量是否和已知匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案對應的特征向量相似，如果相似則判斷其匹配于編碼參數（n,k,d,D），反之則判斷其不匹配于編碼參數（n,k,d,D）.由于SVM 具有分類速度快以及可對線性不可分的數據進行分類等優點[30-32]，所以可以基于SVM 對糾刪碼修復組分布方案對應的特征向量進行分類，以達到快速檢驗糾刪碼修復組分布方案的目的.

EVA 的工作流程如算法1 所示.

算法1.EVA 算法.

1）初始訓練集獲取

EVA按4 步獲取用于構造初始SVM 分類器的訓練集：

①隨機抽取部分編碼參數下的部分糾刪碼修復組分布方案（不妨設糾刪碼修復組分布方案的集合為TE）；

② 將TE中的糾刪碼修復組分布方案及其對應的編碼參數轉換為定長特征向量；

③對于TE中的任意一個糾刪碼修復組分布方案E，枚舉其對應的糾刪碼Tanner 圖，并使用糾刪碼Tanner 圖匹配于指定編碼參數（n,k,d,D）的充要條件來檢驗這些糾刪碼Tanner 圖是否存在1 個匹配（n,k,d,D），從而判斷E是否匹配于（n,k,d,D），即得到E對應定長特征向量的類別標簽；

④ 將所有打上類別標簽的特征向量組合為SVM 分類器的初始訓練集（算法1 的行①～⑧），由于當云數據中心數N固定時，所有糾刪碼修復組分布方案的特征向量長度相同，所以同一套部署環境下只需要準備一份初始訓練集.

2）分類器增量更新

SVM 的分類器的本質是一個能將高維空間一分為二的決策超平面，而其分類特征向量的本質則是判斷被投射到高位空間后的特征向量位于決策超平面的哪一側.在SVM 中，能夠對決策超平面（分類器）的構造造成影響的特征向量為有效特征向量.當初始訓練集中的有效特征向量的數目有限時，首次訓練出的分類器很難反映真實的數據分布情況，使得其無法對特征向量進行準確分類.針對這個問題，基于SVM 的EVA 將在訓練分類器時篩選出訓練集中的有效特征向量，并在分類的同時持續收集新的已知確切類別的特征向量.然后，EVA 將挑選部分新收集的特征向量與舊訓練集中的有效特征向量組成新的訓練集，并使用新的訓練集訓練出一個新的分類器（算法1 的行 ?～?）.因為新的訓練集同時包含新收集的特征向量中的有效特征向量和舊訓練集中有效特征向量，所以新的分類器的分類準確性更高.

增量學習的關鍵是如何從舊訓練集中挑選出有效特征向量以及如何獲取新的有效特征向量：

①舊的訓練集的有效特征向量.EVA 會在訓練分類器的同時獲取一組支持向量，這些支持向量決定了決策超平面.也就是說，這些支持向量即為舊訓練集中的有效特征向量.因此，EVA 直接將這些支持向量加入到新的訓練集中.

② 新收集的特征向量中的有效特征向量.如果分類器對一個特征向量進行了誤分類，那么意味著現有的分類器（決策超平面）缺少該特征向量的信息.因此，如果將該特征向量加入到新的訓練集中，新的決策超平面將與舊的決策超平面有所不同.所以，新收集的特征向量中被舊分類器錯誤分類的部分即為有效特征向量.因此，EVA 將這些支持向量加入到新的訓練集中.

具體而言，EVA 搜集新的有效特征向量以及檢驗糾刪碼修復組分布方案的具體過程如圖5 所示.

Fig.5 Verification process of erasure code repair group distribution scheme圖5 糾刪碼修復組分布方案檢驗過程

首先，EVA 分別用糾刪碼修復組分布方案匹配于指定編碼參數的必要條件和分類器來檢驗輸入的糾刪碼修復組分布方案.

如果分類器和糾刪碼修復組分布方案匹配于指定編碼參數的必要條件的檢驗結果均為某個糾刪碼修復組分布方案E匹配于編碼參數（n,k,d,D），EVA則使用糾刪碼Tanner 圖匹配于指定編碼參數的充要條件來檢驗E的糾刪碼Tanner 圖.如果存在一個E的糾刪碼Tanner 圖匹配于編碼參數（n,k,d,D），則可確定E匹配于編碼參數（n,k,d,D）.反之，如果不存在任何一個E的糾刪碼Tanner 圖匹配于編碼參數（n,k,d,D），則可確定E不匹配于編碼參數（n,k,d,D）且分類器對E對應的的特征向量進行了錯誤分類，此時E對應的特征向量將被加入新的訓練集（算法1 的行?～?）.

如果分類器的分類結果是某個糾刪碼修復組分布方案E不匹配于編碼參數（n,k,d,D），EVA 將在較小的概率Po下使用糾刪碼Tanner 圖匹配于指定編碼參數的充要條件對E進行檢驗（以檢驗分類器的分類結果）——因為分類器誤分類頻率越小，檢驗它的分類結果的必要性越小，所以Po始終等于分類器的當前誤分率.如果存在一個E的糾刪碼Tanner 圖符合其匹配于指定編碼參數的充要條件，可以確定E匹配于編碼參數（n,k,d,D）且分類器對E進行了錯誤分類，此時E對應的特征向量將被加入新的訓練集.如果EVA 沒有使用糾刪碼Tanner 圖匹配于指定編碼參數的充要條件對E進行檢驗或者不存在一個對應于E的糾刪碼Tanner 圖符合其匹配于指定編碼參數的充要條件，那么EVA 將E視為不通過檢驗的糾刪碼修復組分布方案（算法1 的行?～?）.

如果分類器的分類結果是某個糾刪碼修復組分布方案E匹配于編碼參數（n,k,d,D）但E不符合其匹配于指定編碼參數的必要條件，那么可以確定E不匹配于編碼參數（n,k,d,D）且分類器對其進行了誤分類，此時E對應的特征向量將被加入新的訓練集（算法1 的行?～?）.

3.3 近似最優糾刪碼修復組分布方案搜索算法

3.2 節提出EVA 可快速檢驗糾刪碼修復組分布方案是否匹配于指定編碼參數（n,k,d,D）.DSAOE 可從所有能通過EVA 檢驗的糾刪碼修復組分布方案中挑選出具有最小平均跨云數據中心修復流量的一個糾刪碼修復組分布方案.

根據定義6，當云數據中心數目N、編碼參數n以及條帶分布方案確定時，相應的所有糾刪碼修復組分布方案均可被枚舉出來.此外，每個糾刪碼修復組分布方案對應一個平均跨云數據中心修復流量.

因此，DSAOE 的主要思想是：當云數據中心數N,編碼塊數n和編碼塊分布方案被指定后，枚舉出所有與它們相對應的糾刪碼修復組分布方案，并將這些糾刪碼修復組分布方案按它們對應的平均跨云數據中心修復流量遞增的順序排序.然后，對糾刪碼修復組分布方案進行分組并采用多個計算節點對各組糾刪碼修復組分布方案進行并行檢驗——各個計算節點使用EVA 對其進行檢驗.各個計算節點中第一個通過EVA 檢驗的糾刪碼修復組分布方案即為局部最小跨云數據中心修復流量糾刪碼修復組分布方案.各個計算節點的局部最小跨云數據中心修復流量糾刪碼修復組分布方案中具有最小平均跨云數據中心修復流量的一個糾刪碼修復組分布方案即為DSAOE 的輸出.

DSAOE 使用1 個協調者節點和多個工作節點來并行完成最優糾刪碼修復組分布方案的搜索，其具體分工為：

1）協調者節點

協調者節點的工作流程如算法2 所示.

算法2.DSAOE 的協調節點的工作流程.

輸入：編碼參數（n,k,d,D），云數據中心總數N，編碼塊分布方案R，Worker總數W；

輸出：全局最優解GO（包括近似最小跨云數據中心修復流量修復組分布方案及其對應的最優糾刪碼Tanner 圖和平均跨云數據中心修復流量）.

當協調者節點接收到編碼參數（n,k,d,D）、云數據中心總數N以及條帶的編碼塊分布方案R后，協調者節點將枚舉所有可能的糾刪碼修復組分布方案并計算出這些糾刪碼修復組分布方案的平均跨云數據中心修復流量（算法2 的行②）——根據定義6，糾刪碼的修復組分布方案E的平均跨云數據中心流量為（C為E中的編碼塊修復組分布方案、n為一個編碼條帶中的編碼塊數），所以協調者節點計算糾刪碼修復組分布方案的平均跨云數據中心修復流量的開銷較低.

然后，協調者節點將這些糾刪碼修復組分布方案隨機分成若干子集并分發到若干工作節點進行檢驗（算法2 的行③④）.工作節點檢驗這些子集時，協調者節點負責維護臨時全局近似最小跨云數據中心修復流量糾刪碼修復組分布方案及其對應的臨時全局近似最小平均跨云數據中心修復流量（算法2 的行⑤～?）.

2）工作節點

工作節點的工作流程如算法3 所示.

算法3.DSAOE 的工作節點的工作流程.

輸入：編碼參數（n,k,d,D），編碼塊分布方案R，糾刪碼修復組分布方案組subSet，云數據中心數N，分類器svm；

在接收到協調者節點發來的糾刪碼修復組分布方案的集合后，各個工作節點首先將這些糾刪碼修復組分布方案按平均跨云數據中心修復流量遞增的順序進行排列（算法3 的行①）.然后，工作節點依次讀取這些糾刪碼修復組分布方案.如果一個糾刪碼修復組分布方案的平均跨云數據中心修復流量小于臨時全局近似最小平均跨云數據中心修復流量，那么工作節點將使用EVA 對其進行檢驗.第1 個通過EVA 的檢驗的即為局部最低跨云數據中心修復流量糾刪碼修復組分布方案，其對應的平均跨云數據中心修復流量即為局部近似最小平均跨云數據中心修復流量.一旦一個工作節點得到了局部最低跨云數據中心修復流量糾刪碼修復組分布方案和局部近似最小平均跨云數據中心修復流量，它便立即停止后續糾刪碼修復組分布方案的檢驗，并分別用它的局部最低跨云數據中心修復流量糾刪碼修復組分布方案和局部近似最小平均跨云數據中心修復流量來更新協調者節點中的臨時全局最低跨云數據中心修復流量糾刪碼修復組分布方案和臨時全局近似最小平均跨云數據中心修復流量（算法3 的行②～?）.

當所有的工作者節點均停止檢驗糾刪碼修復組分布方案時，協調者節點中的臨時全局近似最小跨云數據中心修復流量糾刪碼修復組分布方案和臨時全局近似最小平均跨云數據中心修復流量即為DSAOE 得到的近似最小跨云數據中心修復流量糾刪碼修復組分布方案和平均跨云數據中心修復流量近似下限.

由于在EVA 的分類器將一個糾刪碼修復組分布方案分為正類后，EVA 還會使用糾刪碼Tanner 圖匹配于指定編碼參數的充要條件對其進行檢驗，因此DSAOE 得到的全局最優糾刪碼修復組分布方案一定匹配于編碼參數（n,k,d,D）.

如果EVA 的誤報率為0，DAOSE 可獲得所有通過EVA 檢驗的糾刪碼修復組分布方案中平均跨數據中心修復流量最小的一個.根據定理5，該糾刪碼修復組分布方案能達到相應編碼參數下的平均跨數據中心修復流量下限，即該糾刪碼修復組分布方案為最優糾刪碼修復組分布方案.若EVA 的誤報率P＞0，且一共存在Q個最優糾刪碼修復組分布方案，那么DAOSE 錯過所有最優糾刪碼修復組分布方案的概率不超過PQ.因此，FMEL 可以得到最優碼的概率不低于1-PQ.

此外，因為DSAOE 使用EVA 來對大多數糾刪碼修復組分布方案進行快速檢驗，所以其效率較高.另外，DSAOE 的并行度高的特點可進一步保證其搜索效率.

3.4 基于試錯的糾刪碼修復組分布方案轉換算法

3.3 節提出了DSAOE 能搜索到近似最小跨云數據中心修復流量糾刪碼修復組分布方案.本節提出了一種基于試錯的糾刪碼修復組分布方案轉換算法EST，用于將近似最小跨云數據中心修復流量糾刪碼修復組分布方案轉換為相應的糾刪碼生成矩陣.

EST 的工作流程如算法4 所示.

算法4.EST 算法.

輸入：全局最優解GO（包括近似最小跨云數據中心修復流量糾刪碼修復組分布方案及其對應的最優糾刪碼Tanner 圖和平均跨數據中心修復流量）；

輸出：近似最小跨云數據中心修復流量糾刪碼的生成矩陣G.

1）對于指定的糾刪碼修復組分布方案，DSAOE只有在找到一個與其相對應的匹配于編碼參數（n,k,d,D）的糾刪碼Tanner 圖時才會確認該糾刪碼修復組分布方案匹配于編碼參數（n,k,d,D）.因此，DSAOE 在搜索近似最小跨云數據中心修復流量糾刪碼修復組分布方案的同時也得到了與之相對應的近似最小跨云數據中心修復流量糾刪碼Tanner 圖 T，如算法4 的行①所示.

2）令U為如式（10）所示的柯西矩陣，基于試錯的糾刪碼修復組分布方案轉換算法EST 將構造一個對應于 T 的校驗矩陣H：如果 T的第j個校驗端點覆蓋其第i個變量端點，那么H的第j行i列的值等于U的第j行i列的值.如果 T的第j個校驗端點不覆蓋其第i個變量端點，那么hji的值為0，如算法4的行②所示.

3）EST 獲取H的所有包含n-k行d-1 列的子矩陣的集合SM1以及H的所有包含其對應于任意D個云數據中心的列的子矩陣的集合SM2.根據定義7，SM1和SM2中的任意矩陣均對應于一個 T的子圖，如算法4 的行③④所示.

4）EST 獲取 T的最大匹配.因為 T符合其匹配于指定編碼參數的充要條件的子條件3，其最大匹配中包含n-k個變量端點，不妨設 T 的最大匹配包含,隨后，EST 求得由H的第l1,l2,…,ln-k列組成的子矩陣H1.顯然，H1是一個方陣（n-k行、n-k列）.同時，EST 將H1加入到集合LS中，如算法4的行⑤⑥所示.

5）基于試錯的糾刪碼修復組分布方案轉換算法EST 獲取對應于SM1和SM2中各個矩陣 T的各個子圖的最大匹配.對于SM1和SM2中的各個矩陣Z，如果它對應 T的子圖的最大匹配中包含的所有校驗端點為則將Z的第l1,l2,…,la行組成的子矩陣添加到集合LS中.根據定理3 中的糾刪碼Tanner 圖匹配于指定編碼參數的充要條件的充分性證明的步驟③，LS中的矩陣均為方陣，如算法4 的行⑦～⑩所示.

6）EST 通過初等行變換將LS中的各個矩陣轉換為如式（11）所示的上三角矩陣（轉換過程見定理3中的糾刪碼Tanner 圖匹配于指定編碼參數的充要條件的充分性證明的步驟④），并獲得這些上三角矩陣的對角元素的集合NE=,其中，為不包含的線性多項式，如算法4 的行?所示.

7）EST 考察NE中的各個對角元素是否為0.如果NE中某個元素的值為0（不妨設），則進行操作：對進行加1 操作；更新H，LS；重新構造上三角矩陣并更新集合NE；重新考察NE中各個元素的值.直到NE中的各個元素的值均不為0，如算法4 的行?～?所示，根據定理3 中的糾刪碼Tanner 圖匹配于指定編碼參數的充要條件的證明過程，此時LS中的矩陣均滿秩.其中，LS中的H1滿秩意味著H滿秩.此外，由定理2 可知，LS中的其他矩陣滿秩意味著此時的H對應的糾刪碼CO能夠容忍任意d-1 個編碼塊失效或任意D個云數據中心失效（即H為一個匹配于（n,k,d,D）的校驗矩陣）.事實上，在我們的多次實驗中，初始NE中的各個元素的值全不為0.也就是說，在大多數情況下，不需要對NE、LS和H進行更新即可一次性得到最終的校驗矩陣H.

8）EST 對H執行初等行變換以得到矩H′=然后，EST 構造G′=和.顯然，G′(H′)T=0.因此GHT=G′·(ΔT)-1ΔT(H′)T=G′In×n(H′)T=0.因此，G為對應于H的生成矩陣，即對應于近似最小跨云數據中心修復流量糾刪碼修復組分布方案的生成矩陣，如算法4 的行?所示.

3.5 FMEL 方法描述

低跨云數據中心修復流量的糾刪碼的快速構造方法FMEL 的工作流程如算法5 所示.

算法5.算法FMEL.

輸入：編碼參數（n,k,d,D），云數據中心總數N，編碼塊分布方案R，Worker總數W，云數據中心數N；

輸出：G.

①全局最優解GO←DSAOE（n,k,d,D,N,R,W,N）；

②G←EST（GO）；

③returnG.

首先，FMEL 通過DSAOE 從所有能通過基于SVM 的EVA 的檢驗的糾刪碼修復組分布方案中選出具有較小平均跨云數據中心修復流量的一個糾刪碼修復組分布方案，如算法5 的行①所示.挑選出的糾刪碼修復組分布方案即為近似最小跨云數據中心修復流量糾刪碼修復組分布方案.然后，FMEL 通過EST 將近似最小跨云數據中心修復流量糾刪碼修復組分布方案轉換為相應編碼參數下的近似最小跨云數據中心修復流量糾刪碼生成矩陣G，如算法5 的行②所示.

4 實驗與結果

4.1 方法實現

為了評估FMEL 構造出的近似最小跨云數據中心修復流量糾刪碼的實際性能，我們基于OpenEC[33]和FastDFS[34]實現了FMEL 構造出的糾刪碼.其中，OpenEC 是一種用于在已有的分布式文件系統中實現不同的糾刪碼編碼方法和修復方法的可定制框架，FastDFS 是一種輕量級的文件系統.

具體而言，我們首先在原始的FastDFS 上增加了對OpenEC 的支持.然后，我們在OpenEC 上實現了FMEL，用于構造近似最小跨云數據中心修復流量糾刪碼生成矩陣.最后，基于OpenEC 的編碼方法和修復方法定制功能，實現了近似最小跨云數據中心修復流量糾刪碼的數據編碼方法和數據修復方法.

4.2 實驗環境與參數

實驗部署于UCloud[35]的6 個云數據中心，其中2 個位于北京（記為PEK1 和PEK2）、1 個位于上海（記為SHA）、1 個位于洛杉磯（記為LOS）、1 個位于臺北（記為TPE）、1 個位于廣州（記為CAN）.實驗使用了每個云數據中心的10 個存儲節點（云主機），每個節點配備4 核Intel Cascadelake 6248R 3.0 GHz 處理器，8 GB 內存和1 TB 磁盤，外網最大帶寬為800 Mbps，內網最大帶寬為25 Gbps.

為了評估FMEL 構造出的近似最小跨云數據中心修復流量糾刪碼的性能，我們將其與典型的糾刪碼進行了比較：最優碼構造方法ACIoT 構造出的最優碼（因為原始的ACIoT 只能構造出指定編碼參數（n,k,d）下的最優碼，我們對其進行了擴展，使其能夠構造出指定編碼參數（n,k,d,D）下的最優碼）、一種能夠達到平均局部性下限的糾刪碼ACL 碼[23]、經典的RS 碼[36]、一種典型的局部性碼Xorbas 碼[22]和一種典型的跨云數據中心糾刪碼DFC 碼[13].

為了評估FMEL 構造出的近似最小跨云數據中心修復流量糾刪碼在不同環境中的性能，我們將UCloud 的6 個云數據中心分為了2 個實驗環境.由于大多數的跨云數據中心存儲系統均是部署在3 個云數據中心[1,14]，所以我們的每個實驗環境均包含3個云數據中心.具體而言，實驗環境1 包含PEK1,PEK2,SHA，實驗環境2 包含LOS,TPE,CAN.由于各個實驗環境包含3 個云數據中心，因而容災度D的合理取值范圍為[1,2]，所以實驗中D∈[1,2].此外，在實際應用中，為了便于條帶管理，單個條帶內的編碼塊數n通常較小.因此，我們在實驗中將n的范圍限制在[6,11]（常見的生產系統中的n均處于該范圍內[37-39]）.另外，實驗中單個條帶內的數據塊數k的取值范圍為[n/3,2n/3]，因為當k屬于此范圍時D的取值范圍為[1,2].最后，容錯度d的取值范圍為[2,n-k+1]，即d的合理取值范圍[1,12-18].

在本文實驗中，各個編碼條帶的編碼塊被平均分配到各個云數據中心中，以獲取較高的容災度和負載均衡性.此外，新生節點與其相應的失效編碼塊位于同一云數據中心，以保持系統的容災度和負載均衡性.實驗中的編碼塊大小和HDFS 一致[35]，為128 MB.

4.3 評價指標

我們用4 個指標來評價FMEL 的性能：

1）分類器誤報率（false-negative rate,FN）.假設被FMEL 中的SVM 分類器誤分類為負類（不滿足編參數（n,k,d,D）的類）的糾刪碼修復組分布方案的數目為f1，EVA 檢驗過的糾刪碼修復組分布方案中匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案數為f2，那么分類器誤報率為f1/f2.

2）糾刪碼構建時間（construction time,CT）.糾刪碼構造時間是指ACIoT 構造最優碼的時間或FMEL構造近似最小跨云數據中心修復流量糾刪碼的時間.

3）平均跨云數據中心修復流量T.令某糾刪碼修復它的一個條帶中的n個編碼塊產生的跨云數據中心修復流量分別為T1,T2,…,Tn且每個編碼塊的大小為m，那么該糾刪碼的平均跨云數據中心修復流量

4）平均修復用時t.令某糾刪碼在實驗環境1 中修復它的一個條帶中的n個編碼塊所消耗的時間分別為t1,1,t1,2,…,t1,n，在實驗環境2 中修復它的一個條帶中的n個編碼塊所消耗的時間分別為t2,1,t2,2,…,t2,n,每個編碼塊的大小為m.因為tj,i受到云數據中心的排列順序的影響，令為tj,i在不同云數據中心的排列順序下的平均值.那么，該糾刪碼的平均修復用時

4.4 分類器誤報率

在FMEL 中，SVM 分類器將一個糾刪碼修復組分布方案分為正類后，還會使用糾刪碼Tanner 圖匹配于指定編碼參數的充要條件對其進行檢驗，因此FMEL 不會將不匹配于編碼參數（n,k,d,D）糾刪碼修復組分布方案錯誤分為正類.此外，如果SVM 分類器將一個匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案錯誤分為負類，FMEL 可能會錯過具有較小平均跨云數據中心修復流量且匹配于編碼參數（n,k,d,D）的糾刪碼修復組分布方案.因此，我們主要關注分類器將糾刪碼修復組分布方案錯誤分為負類的概率，即誤報率.

我們的測試數據包括所有編碼參數下的所有糾刪碼修復組分布方案.在分類器初始化時，首先在各組編碼參數下隨機挑選了50 個糾刪碼修復組分布方案并將這些糾刪碼修復組分布方案轉換為對應的特征向量.然后，使用糾刪碼修復組分布方案匹配于編碼參數（n,k,d,D）的充要條件判斷這些糾刪碼修復組分布方案是否滿足各自的編碼參數，并以此為依據為對應的特征向量打上標簽.因此，我們可以得到這些糾刪碼修復組分布方案對應的帶標簽的特征向量，它們組成了分類器的初始訓練集（10 次實驗的平均初始訓練集構造用時為1 711 s、平均初始分類器構造用時為192 s）.然后，我們按編碼參數n遞增的順序將其他的糾刪碼修復組分布方案輸入到分類器中進行分類.與此同時，FMEL 不斷搜集新的訓練集對分類器進行增量更新.

分類器分類每組（n,k）對應的所有糾刪碼修復組分布方案的誤報率如圖6 所示.因為在分類過程中含有效信息的特征向量被逐漸加入到新的訓練集中，并不斷更新分類器，因此分類器的誤報率隨著n的增加而逐漸降低.

Fig.6 False-negative rate of SVM’s classifier圖6 SVM 分類器的誤報率

因為同一組編碼參數下的最優碼往往存在多個，所以最優糾刪碼修復組分布方案也往往存在多個.假設一共存在Q個最優糾刪碼修復組分布方案且分類器的誤報率為P，那么FMEL 錯過所有最優糾刪碼修復組分布方案的概率不超過PQ.因此，FMEL 可以得到最優碼的概率不低于1-PQ.由圖6 可知，P總是小于27%的.所以，如果Q＞1，FMEL 有92.7%的概率得到最優碼；如果Q＞2，FMEL 則有98%的概率得到最優碼.

4.5 糾刪碼構造時間

每組（n,k）對應多組（n,k,d,D），FMEL 和ACIoT在每組（n,k）對應的所有（n,k,d,D）下的糾刪碼構造時間如圖7 所示（FMEL 的工作節點數和ACIoT的工作進程數均為5）.在構造最優碼或近似最小跨云數據中心修復流量糾刪碼時，ACIoT 和FMEL 均需要枚舉和檢驗部分糾刪碼修復組分布方案的糾刪碼Tanner 圖.由于編碼參數（n,k,d,D）下的糾刪碼Tanner圖的總數為2n(n-k)，所以，通常而言，n(n-k)越大，ACIoT和FMEL 需要檢驗的糾刪碼Tanner 圖越多.因此，ACIoT和FMEL 的糾刪碼構造時間均呈現出隨著n(n-k)的減少而減少的趨勢.

Fig.7 Erasure code construction time of ACIoT and FMEL圖7 ACIoT 和FMEL 的糾刪碼構造時間

對于大部分的糾刪碼修復組分布方案，FMEL 僅需要用SVM 分類器對它們分類即可，無需枚舉和檢驗它們對應的糾刪碼Tanner 圖.因此，FMEL 的平均糾刪碼構造時間僅為ACIoT 的11%.特別地，當n(n-k)較小時，總的糾刪碼構造時間較短.所以，此時FMEL中更新分類器的時間占總的糾刪碼構造時間的比例較大.因此，此時FMEL 的糾刪碼構造時間比ACIoT 略長.

4.6 平均跨云數據中心修復流量

因為不同的糾刪碼適應的編碼參數不同，我們首先在除RS 碼外的所有糾刪碼都適應的編碼參數下比較了各個糾刪碼的平均跨云數據中心修復流量（RS碼使用和其他糾刪碼相近的編碼參數），如圖8 所示.在這些編碼參數下，DFC 碼和ACIoT 均可為每個云數據中心分配一個局部校驗塊，因此，DFC 和ACIoT 均能夠在不跨云數據中心傳輸數據的情況下完成編碼塊的修復，因而它們的平均跨云數據中心修復流量為0.大多數情況下，FMEL 的平均跨云數據中心修復流量也為0，即FMEL 有較大概率得到最優碼.

Fig.8 Average cross-cloud data center repair traffic of ACL,Xorbas,DFC,RS,ACIoT and FMEL圖8 ACL 碼、Xorbas 碼、DFC 碼、RS 碼、ACIoT 和FMEL 的平均跨云數據中心修復流量

因為RS 碼在修復任意一個編碼塊時均需要讀取k個編碼塊，而在實驗中使用的全部編碼參數下各編碼條帶在同一個云數據中心的編碼塊數始終小于k（如果要使各編碼條帶在同一個云數據中心的編碼塊數始終不小于k，那么冗余度將十分大），所以RS碼在修復任意一個編碼塊時均需要跨云數據中心傳輸數據.因此，RS 碼跨云數據中心修復流量最大.

因為Xorbas 碼和ACL 碼具有較低的修復流量（其中ACL 碼能夠達到平均修復流量的下限），所以它們能在一定程度上降低平均跨云數據中心修復流量，進而使得它們的平均跨云數據中心修復流量相較于局部性為k-1 的RS 碼更小.但是，由于修復流量不與跨云數據中心修復流量嚴格正相關，所以ACL碼和Xorbas 碼的平均跨云數據中心修復流量大于ACIoT,FMEL,DFC 碼.

因為RS 碼和DFC 碼對編碼參數的限制較為嚴格，我們在更多的編碼參數下比較了其他糾刪碼.如圖9 所示，在這些編碼參數下，FMEL 的平均跨云數據中心修復流量比ACL 碼和Xorbas 碼分別低了24.0%和34.8%，這是因為FMEL 能在這些參數下達到平均跨云數據中心修復流量的近似下限.

Fig.9 Average cross-cloud data center repair traffic of ACL,Xorbas,ACIoT and FMEL圖9 ACL 碼、Xorbas 碼、ACIoT 和FMEL 的平均跨云數據中心修復流量

平均而言，FMEL 的平均跨云數據中心修復流量比ACL 碼、Xorbas 碼和RS 碼分別低了42.9%,51.1%,56.0%.此外，FMEL 的平均跨云數據中心修復流量與DFC 碼相近，但DFC 碼對編碼參數限制嚴格.

另外，FMEL 的平均跨云數據中心修復流量是ACIoT的100%～133%，并且在實驗采用的15 組編碼參數中的13 組編碼參數下，FMEL 的平均跨云數據中心修復流量與ACIoT 相同，即FMEL 構造出最優碼的概率較高.

容錯度d和FMEL 構造的近似最小跨云數據中心修復流量糾刪碼的平均跨云數據中心修復流量之間的關系如圖10 所示，當d小于一個特定值d'后，近似最小跨云數據中心修復流量糾刪碼的平均跨云數據中心修復流量,即平均跨云數據中心修復流程近似下限.這是因為當d＜d'時，的主要影響因素為容災度D.基于這一發現，不僅能夠得到編碼參數（n,k,D）下的平均跨云數據中心修復流量的近似下限，還可以得到滿足該近似下限時的d的上限，即圖中的最優d.

Fig.10 Relationship between d and average cross-cloud data center repair traffic’s approximate lower bound under different n,k,D圖10 不同n,k,D 下d 與平均跨云數據中心修復流量近似下限的關系

因為與最優d相對應的編碼參數和近似最小跨云數據中心修復流量糾刪碼能夠在冗余度()、容錯度(d)、容災度(D)和平均跨云數據中心修復流量()之間取得較好權衡，因此關于最優d的這一發現對于實際應用具有指導意義.比如說，基于這一發現，我們找到了2 個能夠在冗余度、容錯度、容災度和平均跨數據修復流量之間取得較好權衡的糾刪碼——FMEL（n=6,k=2）和FMEL（n=9,k=5，其生成矩陣如式（12）和式（13）所示.

如表2 所示，FMEL（n=6,k=2）的d值比3 副本技術高66.7%，同時，FMEL（n=6,k=2）的D、和和3 副本技術相同.此外，FMEL（n=9,k=5）的D比2 副本技術高33.3%，同時FMEL（n=9,k=5）的和比2副本技術低10%和33%且二者D相同.

Table 2 Comparison Between FMEL and Replications表2 FMEL 與多副本的對比

4.7 平均修復用時

因為不同的糾刪碼適應的編碼參數不同，我們首先在除RS 碼外的所有糾刪碼都適應的編碼參數下比較了各個糾刪碼的平均修復用時（RS 碼使用和其他糾刪碼相近的編碼參數），如圖11 所示.

Fig.11 Average repair time of ACL,Xorbas,DFC,RS,ACIoT and FMEL圖11 ACL 碼、Xorbas 碼、DFC 碼、RS 碼、ACIoT 和FMEL 的平均修復用時

由于FMEL 和ACIoT 的平均跨云數據中心修復流量小于對照組中的其他糾刪碼，其修復數據時跨云數據中心傳輸數據的時間較短，使得其平均修復用時也比其他糾刪碼少.具體地，FMEL 的平均修復用時比ACL 碼、Xorbas 碼和RS 碼分別少了36.9%,46.1%,50.6%.此外，ACIoT 的平均修復用時與FMEL相近，但是ACIoT 的糾刪碼構造時間更長.

因為RS 碼和DFC 碼的編碼參數適應性較差，我們在更多的編碼參數下對除這2 種糾刪碼之外的糾刪碼進行了對比，如圖12 所示.在這些編碼參數下，FMEL 和ACIoT 的平均修復用時少于ACL 碼和Xorbas碼，這是因為基于FMEL 和ACIoT 的平均跨云數據中心修復流量較小.特別地，在編碼參數為（8,3,5,1）時，FMEL 和ACIoT 的平均修復用時遠低于其他糾刪碼，因為此時只有它們能夠在不跨云數據中心傳輸數據的情況下完成數據修復.

Fig.12 Average repair time of ACL,Xorbas,ACIoT and FMEL圖12 ACL 碼、Xorbas 碼、ACIoT 和FMEL 的平均修復用時

此外，如表2 所示，因為FMEL（n=9,k=5）的平均跨云數據中心修復流量低于2 副本技術，因此其平均修復用時也短于2 副本技術.特別地，雖然FMEL（n=6,k=2）的平均跨云數據中心修復流量與3副本技術相同，但其平均修復用時略長于3 副本技術，這是因為FMEL（n=6,k=2）在修復數據時的計算量大于3 副本技術.

5 總結

針對現有糾刪碼構造方法無法兼顧編碼參數適應性、跨云數據中心修復流量和糾刪碼構造效率的問題，本文提出了一種低跨云數據中心修復流量的糾刪碼的快速構造方法FMEL，可在不同編碼參數下快速求得低跨云數據中心修復流量糾刪碼.在真實跨云數據中心環境中的實驗表明，相較于現有的可構造能達到平均跨云數據中心修復流量下限的最優碼的方法，FMEL 構造糾刪碼的時間少了89%，且在大部分編碼參數下二者構造的糾刪碼的平均跨云數據中心修復流量相同.此外，我們利用FMEL 評估了大量編碼參數，并挑選出2 組編碼參數.FMEL 在這2 組編碼參數下構造的糾刪碼的平均修復流量低于已得到廣泛使用的多副本技術，同時其容災性、容錯性和冗余度相較于多副本技術具有明顯優勢.

作者貢獻聲明：包涵提出了算法思路和實驗方案，并負責完成實驗和撰寫論文；王意潔提出指導意見并修改論文.