復(fù)雜載荷簡化對梁內(nèi)力和變形的影響

李銀山， 薛春霞， 韓 蕾， 李尚志， 葉紅玲

（1.河北工業(yè)大學(xué)機械工程學(xué)院，天津 300401；2.海南大學(xué)土木建筑工程學(xué)院，海口 570228；3.山東工程職業(yè)技術(shù)大學(xué)建筑工程學(xué)院，濟南 250200；4.北京航空航天大學(xué)數(shù)學(xué)科學(xué)學(xué)院，北京 100191；5.北京工業(yè)大學(xué)材料與制造學(xué)部，北京 100124）

0 引言

鋼筋混凝土簡支板橋是小跨度橋梁最常用的結(jié)構(gòu)形式之一，在國內(nèi)外被廣泛地使用于中小城市的公路主干線上，在城市交通中發(fā)揮著重要作用。因此簡支梁力學(xué)模型是教學(xué)中最常使用的力學(xué)簡化模型之一［1］。針對梁的彎曲變形，研究者提出了多種方法［2-4］。如奇異函數(shù)法可以很簡潔地獲得整根階梯形梁的撓度方程［5］，并推廣應(yīng)用于多層框架結(jié)構(gòu)［6］。但應(yīng)用函數(shù)表達(dá)的撓度形式復(fù)雜。林金木［7］提出了一種新方法推導(dǎo)出梁在任意荷載下的撓度曲線表達(dá)式。李彤等［8-9］對三鉸拱橋結(jié)構(gòu)的靜力分析和影響線進行了研究。積分法是基本的計算方法，其優(yōu)越性在于可用解析方法得到撓度方程和轉(zhuǎn)角方程，求解平面彎曲梁的撓度和轉(zhuǎn)角，可用載荷方程積分法［10］，需要對撓度的撓曲線近似微分方程進行4 次積分運算并結(jié)合邊界條件才能得到撓度。對于簡單的線性分布載荷表達(dá)式，可由載荷方程積分法獲得彎曲變形的精確解，但是，對于表達(dá)式復(fù)雜的非線性分布載荷，由于函數(shù)表達(dá)式的不可積，很難得到它的精確解［11］。李銀山［12］提出的連續(xù)分段獨立一體化積分法是一種快速求解結(jié)構(gòu)彎曲變形問題的解析方法，求解了復(fù)雜載荷作用下變剛度超靜定梁彎曲變形的解析解［13］。

本文利用連續(xù)分段獨立一體化積分法求解復(fù)雜載荷作用下簡支梁的彎曲變形解析解。針對復(fù)雜的非線性分布載荷表達(dá)式，首先利用函數(shù)的泰勒級數(shù)展開法，分別選取前4 項，將復(fù)雜分布載荷簡化成均布載荷、線性分布載荷、拋物線分布載荷和三次多項式分布載荷。再將梁進行連續(xù)分段離散化，按等步長分成m等分，并利用最小二乘法回歸成n次多項式，分別求解梁的內(nèi)力和變形，并進行相對誤差計算和其對各多項式系數(shù)靈敏度分析。

1 問題的提出

圖1 所示為承受復(fù)雜載荷的簡支梁，設(shè)長為L、抗彎剛度為EI的簡支梁，承受分布載荷q（x），集中載荷F和集中力偶Me。作用在梁上的分布載荷

圖1 承受復(fù)雜載荷的簡支梁

求解梁的內(nèi)力與變形。式中：x為距離原點A的位置；q0為最大值。

復(fù)雜分布力最大值

簡支梁的撓曲線微分方程為

式中：v為撓度；EI為梁的彎曲剛度。

邊界條件為：

為了便于編程計算，引入變量：

并定義：

同時，將方程式（3）無量綱化，并將式（1）代入可得：

邊界條件為：

由于任意函數(shù)f（X）可以展開為X的泰勒級數(shù)［14-15］，可得

將式（7）離散化，按等步長將梁分成m等分，利用最小二乘法回歸成n次多項式。n次多項式系數(shù)，原函數(shù)式（9）離散化等分?jǐn)?shù)m與分布載荷相對誤差對照表見表1 和表2 所示。相對誤差為

表1 分布載荷函數(shù)離散化等分?jǐn)?shù)、多項式系數(shù)對照表

表2 分布載荷函數(shù)離散化等分?jǐn)?shù)與相對誤差對照表%

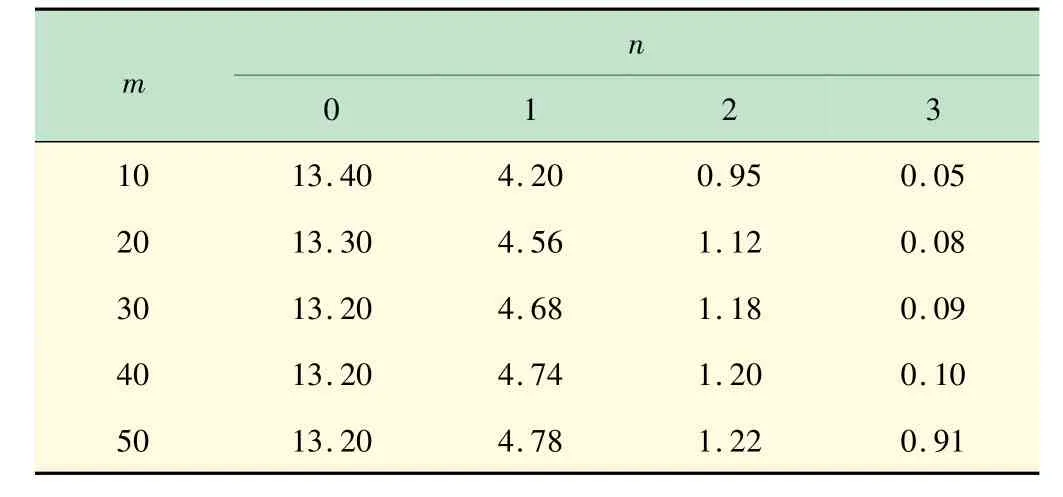
表2 分布載荷函數(shù)離散化等分?jǐn)?shù)與相對誤差對照表%

n m 01 23 1013.404.200.950.0520 13.304.561.120.0830 13.204.681.180.0940 13.204.741.200.1050 13.204.781.220.91

2 復(fù)雜分布載荷的簡化（以m=20 為例）

2.1 將復(fù)雜分布載荷簡化成均布載荷

工程中經(jīng)常將分布載荷簡化成均布載荷，如圖2所示。在式（9）中的展開式只取常數(shù)項（n=0），即：

圖2 均布荷載與原分布荷載

將梁分成兩段k=2，簡支梁的撓曲線微分方程為：

其邊界條件和連續(xù)光滑條件為：

用連續(xù)分段獨立一體化積分法求解，得到：

（1）剪力函數(shù)

（2）彎矩函數(shù)

（3）轉(zhuǎn)角函數(shù)

（4）撓度函數(shù)

n=0 時，對應(yīng)簡支梁的內(nèi)力和變形，如圖3 所示。

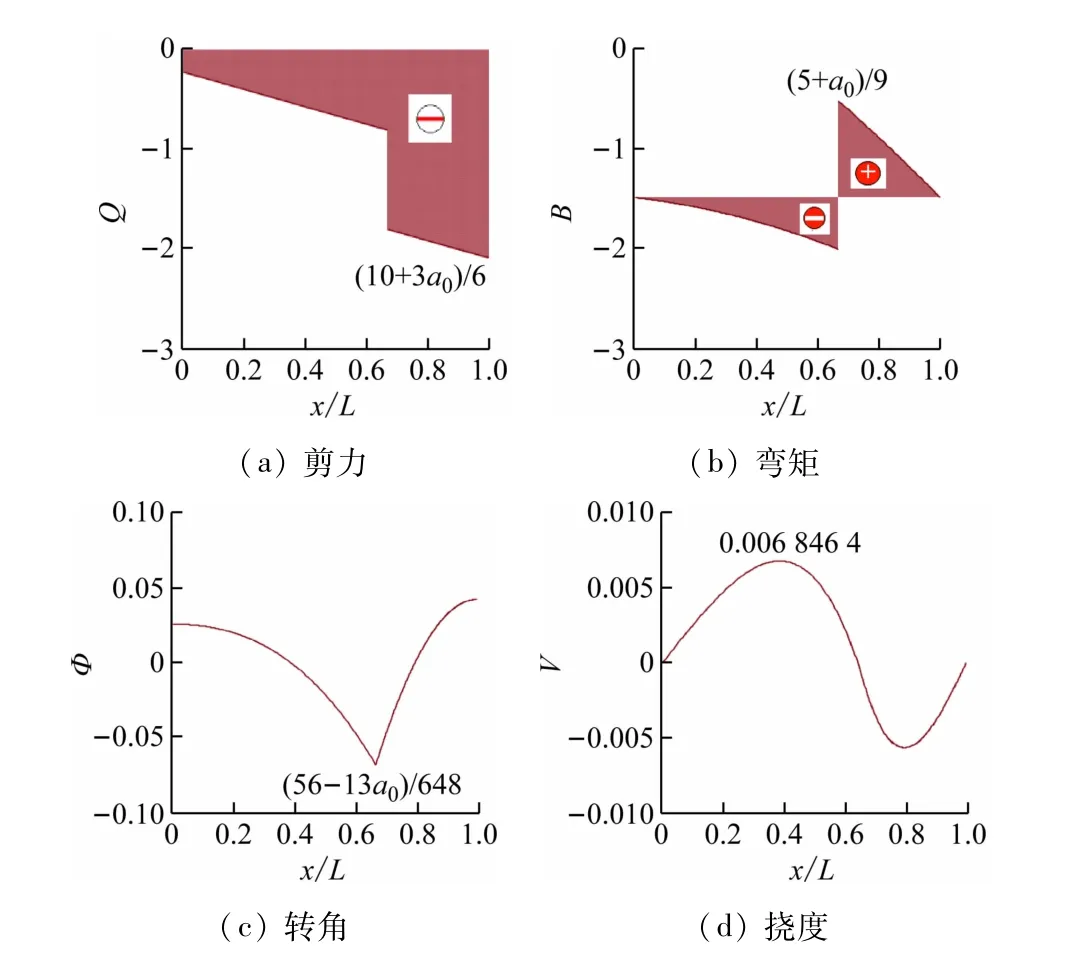
圖3 n=0時簡支梁的內(nèi)力和變形圖

圖4 線性分布荷載與原分布荷載

由此，得到的最大剪力、最大彎矩、最大轉(zhuǎn)角及最大撓度分別為：

2.2 將復(fù)雜分布載荷簡化成線性分布載荷

工程中經(jīng)常將分布載荷簡化成線性分布載荷如圖4 所示，即在式（9）中的展開式中只取一次函數(shù)（n=1），即

利用最小二乘法解得：a0=1.0456，a1= -0.35722。可得分布力最大值：

用同樣方法得到n=1 時，對應(yīng)簡支梁的內(nèi)力圖和變形圖如圖5 所示。

圖5 n=1時簡支梁的內(nèi)力圖和變形圖

得到最大剪力、最大彎矩、最大轉(zhuǎn)角及最大撓度分別為：

階數(shù)相對誤差：

2.3 將復(fù)雜分布載荷簡化成拋物線分布載荷

工程中經(jīng)常將復(fù)雜分布載荷簡化成拋物線分布載荷，如圖6 所示。在式（9）中的展開式中只取二次函數(shù)（n=2），即

圖6 拋物線分布荷載與原分布荷載

利用最小二乘法解得：a0=1.0112，a1= -0.13996，a2= -0.21727。可得分布力最大值：

用同樣方法得到n=2 時，對應(yīng)簡支梁的內(nèi)力圖和變形圖如圖7 所示。

圖7 n=2時簡支梁的內(nèi)力圖和變形圖

相應(yīng)最大剪力、最大彎矩、最大轉(zhuǎn)角及最大撓度分別為：

階數(shù)相對誤差：

2.4 將復(fù)雜分布載荷簡化成三次多項式分布載荷

如圖8 所示，即在式（9）中的展開式中只取3 次函數(shù)（n=3），則

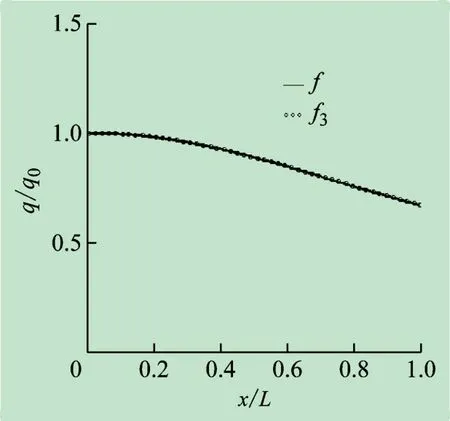
圖8 三次分布荷載與原分布荷載

利用最小二乘法解得：a0=0.99919，a1=0.02417，a2= -0.63775，a3=0.28032。

用同樣方法得到n=3 時，對應(yīng)簡支梁的內(nèi)力圖和變形圖如圖9 所示。相應(yīng)最大剪力、最大彎矩、最大轉(zhuǎn)角及最大撓度分別為：

圖9 n=3時簡支梁的內(nèi)力圖和變形圖

階數(shù)相對誤差：

3 結(jié)果的誤差和靈敏度分析

表3 簡支梁內(nèi)力與變形計算結(jié)果

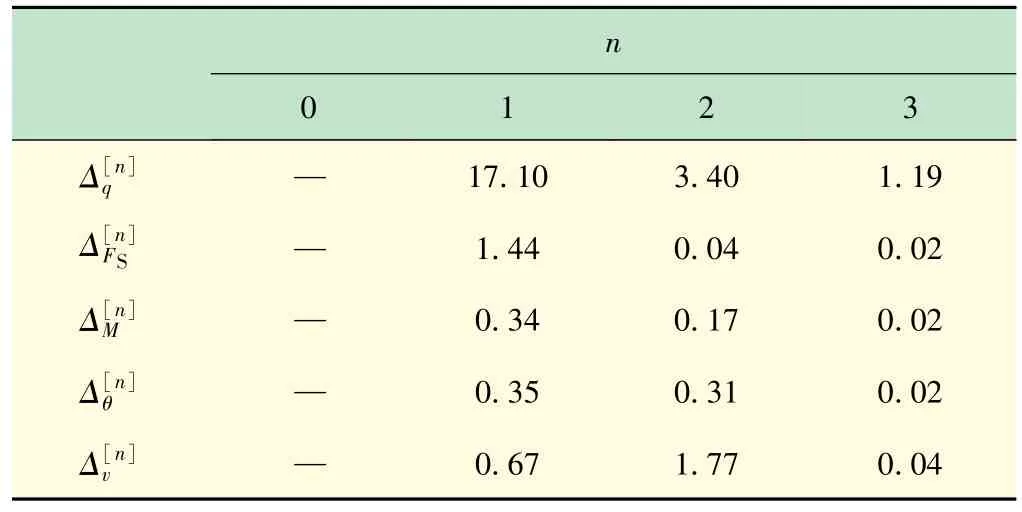
表4 簡支梁內(nèi)力與變形的階數(shù)相對誤差%

如果把剪力、彎矩、轉(zhuǎn)角和撓度統(tǒng)一表示為a0，a1，a2，a3的函數(shù)

則函數(shù)的誤差可表示為全微分，即

從而可得簡支梁內(nèi)力與變形的誤差對各多項式系數(shù)靈敏度分析如表5 所示（n=3）。

表5 簡支梁內(nèi)力與變形的誤差對應(yīng)各多項式系數(shù)靈敏度（n=3）

4 結(jié)語

本文針對復(fù)雜載荷作用下簡支梁的彎曲變形問題，利用函數(shù)的泰勒級數(shù)展開法，分別選取前四項，將復(fù)雜分布載荷簡化成均布載荷、線性分布載荷、拋物線分布載荷和三次多項式分布載荷。利用求解彎曲變形問題的分段獨立一體化積分法，通過Maple求解程序，快速得到其解析解，并進行誤差的靈敏度分析。

結(jié)果表明：按等步長將梁分成20 等分，利用最小二乘法回歸成3 次多項式的分布載荷，簡支梁內(nèi)力與變形的計算結(jié)果滿足收斂要求，階數(shù)相對誤差最小，滿足工程應(yīng)用。本文提出的方法與傳統(tǒng)積分法相比，數(shù)學(xué)模型建立方法簡單，求解數(shù)學(xué)模型只需要分段獨立積分，采用計算機求解計算速度快，計算結(jié)果滿足工程需求，可以指導(dǎo)橋梁等結(jié)構(gòu)工程設(shè)計。