基于超螺旋觀測器的SPMSM無傳感器控制

楊贄瑋,趙世偉,楊向宇,邱小華

(華南理工大學 電力學院,廣州 510640)

0 引 言

表貼式永磁同步電機(以下簡稱SPMSM)具有結構簡單、可靠性高、功率密度高等優勢,近年來廣泛應用于高性能調速系統[1]。其調速系統的控制方式有矢量控制和直接轉矩控制,前者性能更優異,在實際應用中更加廣泛[2]。矢量控制要求電機反饋準確的轉子位置,其獲取通常依靠加裝在電機轉軸上的機械位置傳感器,繼而帶來了系統可靠性降低、體積增大和成本增加的問題。無傳感器控制通過采樣電機電信號來估計轉子位置,避免了使用位置傳感器[3]。目前,永磁同步電機無傳感器控制已經成為國內外學者研究的熱點[4]。

無傳感器控制的主要方案有Luenberger觀測器、滑模觀測器、模型參考自適應和卡爾曼濾波等。其中,滑模觀測器(以下簡稱SOM)有實現簡單和抗擾強的優勢,但其觀測反電動勢由高頻開關信號組成,導致了波形正弦度低以及嚴重的抖振現象[5]。

文獻[6]在傳統SMO的基礎上使用sigmoid函數替代sign函數,有效減小了抖振。對觀測反電動勢進行濾波可以顯著提高其正弦度,但會引入相位滯后問題。文獻[7]使用濾波后的反電動勢代替濾波前抖動嚴重的反電動勢信號作為滑模觀測器的反饋,改善了濾波環節造成的相位滯后。文獻[8]中,為了避免使用低通濾波器,設計了狀態觀測器觀測反饋信號,該方法實現了較寬的調速范圍,但狀態觀測器的設計與參數設置較復雜。文獻[9]設計了基于飽和函數的滑模觀測器,引入一種截止頻率隨轉子速度變化而變化的低通濾波器,改善了濾波效果,但由于傳統滑模的局限,觀測位置仍有一定的抖動。文獻[10]引入模糊規則,對超螺旋觀測器(以下簡稱STO)參數進行在線整定,提高了觀測器在參數變化情況下的魯棒性,但模糊規則的設計較困難。文獻[11]提出了一種變增益STO,觀測器增益與電機轉速相關,減小了低速時的觀測誤差。

針對SMO的抖振問題,本文設計了STO并對觀測反電動勢進行濾波以削弱高次諧波,設計鎖相環提取轉子位置和轉速信號并對轉子位置進行補償,以減小濾波帶來的相位滯后。最后進行仿真與實驗以驗證本方案的有效性。

1 SPMSM數學模型

SPMSM在α-β坐標系下的數學模型如下:

(1)

式中:uα、uβ,iα、iβ為α-β坐標系下電壓、電流;R和L為定子電阻和電感;ψm為永磁體磁鏈;ωe、θ為電角速度和電角度。

反電動勢表達式:

(2)

式中:eα和eβ為α-β坐標系下的反電動勢。

由式(2)可以得到,SPMSM反電動勢中包含了電機轉速和轉子位置信息。

2 超螺旋滑模觀測器設計

2.1 超螺旋算法

針對傳統SMO固有的抖振問題,文獻[12]提出了超螺旋滑模算法理論,文獻[13]利用李雅普諾夫第二法證明了基于該算法的觀測器在有擾動和無擾動情況下都可以在有限時間收斂。本文的超螺旋算法表示:

(3)

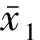
取δ≥0,并假設系統擾動全局有界:

(4)

當增益滿足:

(5)

x=0是全局漸進平衡點,且對于任意初始狀態系統將在有限時間收斂至平衡點。

2.2 基于超螺旋算法的滑模觀測器

由式(1)、式(2)建立以反電動勢形式表示的SPMSM方程:

(6)

電流估計方程表示:

(7)

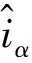
將式(7)與式(6)作差得到電流誤差方程:

(8)

(9)

基于超螺旋算法設計反電動勢估計值:

(10)

觀測反電動勢由兩項組成,前項類似于傳統滑模,但會隨著電流誤差收斂而逐漸減小,后項是一個連續的積分項。

對照式(3)、式(7)可得:

(11)

由式(4)得:

(12)

從式(12)選定合適的δ≥0后,觀測器增益k1、k2應該滿足式(5)的約束,以保證收斂性能。

3 基于鎖相環的轉子位置估計

3.1 基于鎖相環的轉子位置重構

觀測反電動勢中包含了轉子位置信息。傳統方法一般使用反正切函數計算角度,再對角度微分獲得角速度。即:

(13)

觀測反電動勢由高頻信號組成,當其過零時,反正切函數會出現飽和現象,導致估計轉子位置和轉速出現較大的誤差。為了避免這個問題,本文設計鎖相環(以下簡稱PLL)提取轉子位置信息。

PLL結構如圖1所示。

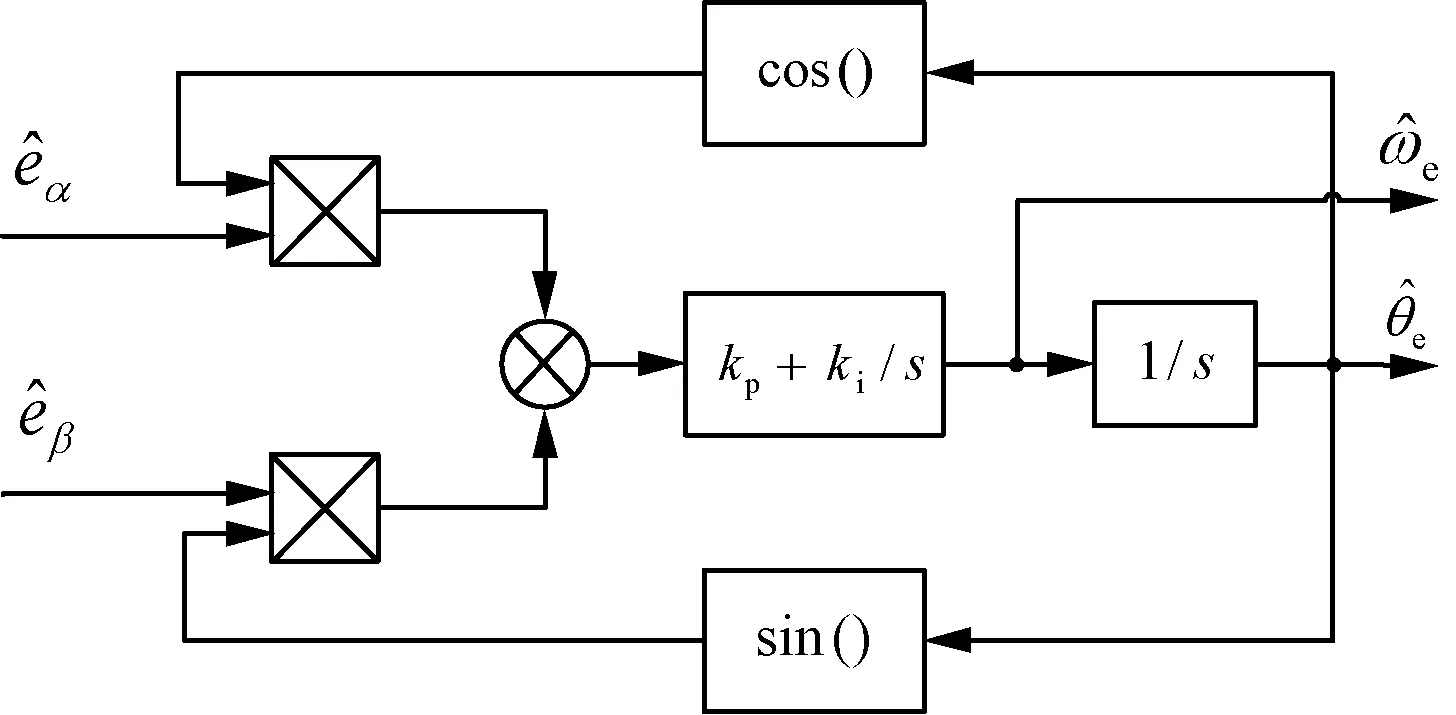
圖1 PLL結構圖

結合式(2)可以得到:

(14)

從而得到傳遞函數:

(15)

通過式(15),可以使用配置帶寬的方式選擇PLL的PI參數。

3.2 反電動勢濾波以及轉子位置自適應補償

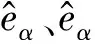
濾波補償框架如圖2所示。

圖2 濾波補償框架圖

輸入PLL的反電動勢表示:

(16)

式中:ωc為截止頻率;ω為反電動勢頻率。

反電動勢經過低通濾波后,相位滯后:

(17)

對應的觀測角度滯后值:

(18)

補償后的電角度:

(19)

4 仿真與實驗結果

4.1 仿真分析

為了驗證本文算法的可行性,在MATLAB/Simulink中搭建如圖3所示的仿真模型。同時,搭建了傳統SMO+PLL模型用于對比。

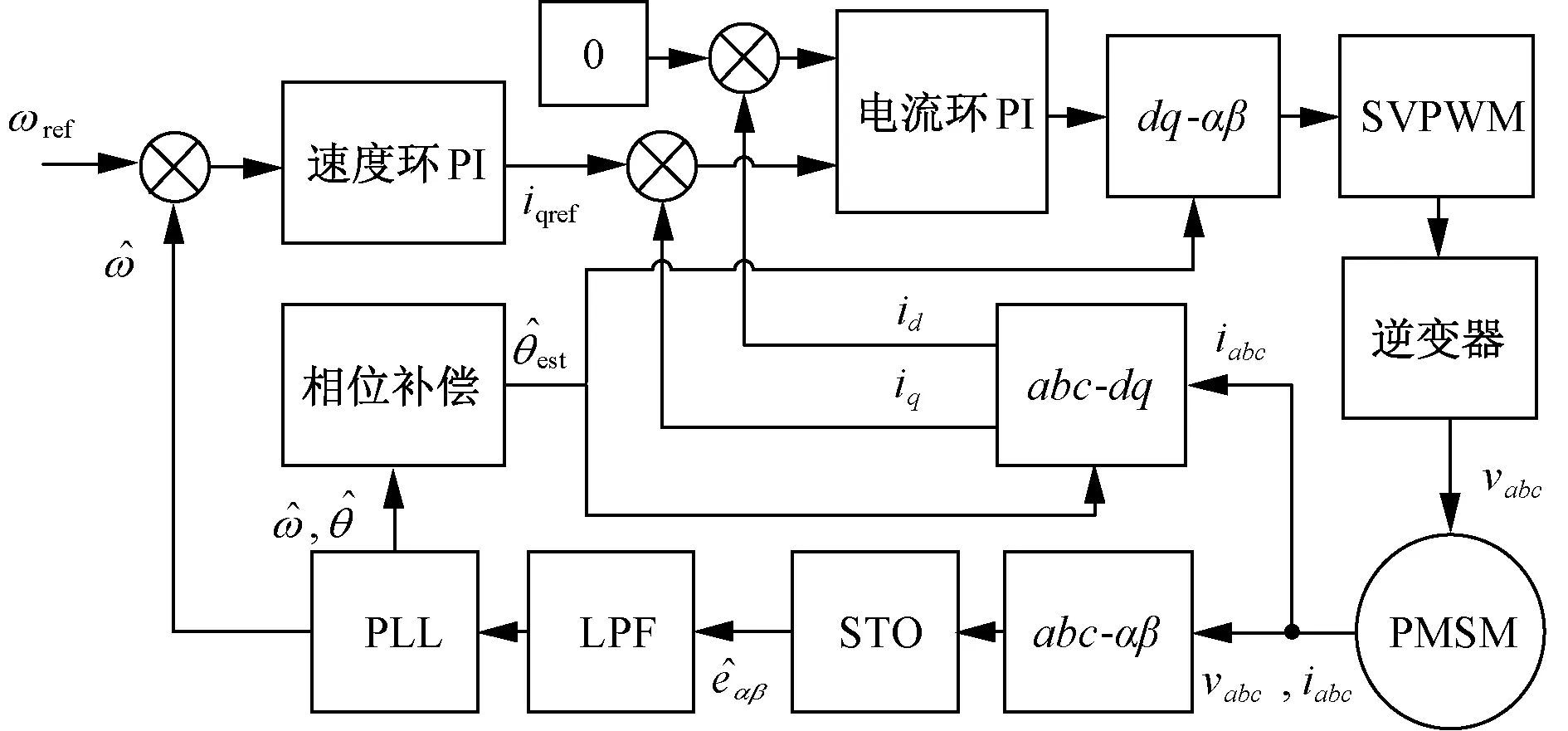
圖3 仿真模型結構框圖

圖3中的PLL為鎖相環,LPF為低通濾波器。STO算法框架如圖4所示。在仿真過程中,設置觀測器增益k1=25,k2=3 000,PLL比例積分環節Kp=900,Ki=160 000。

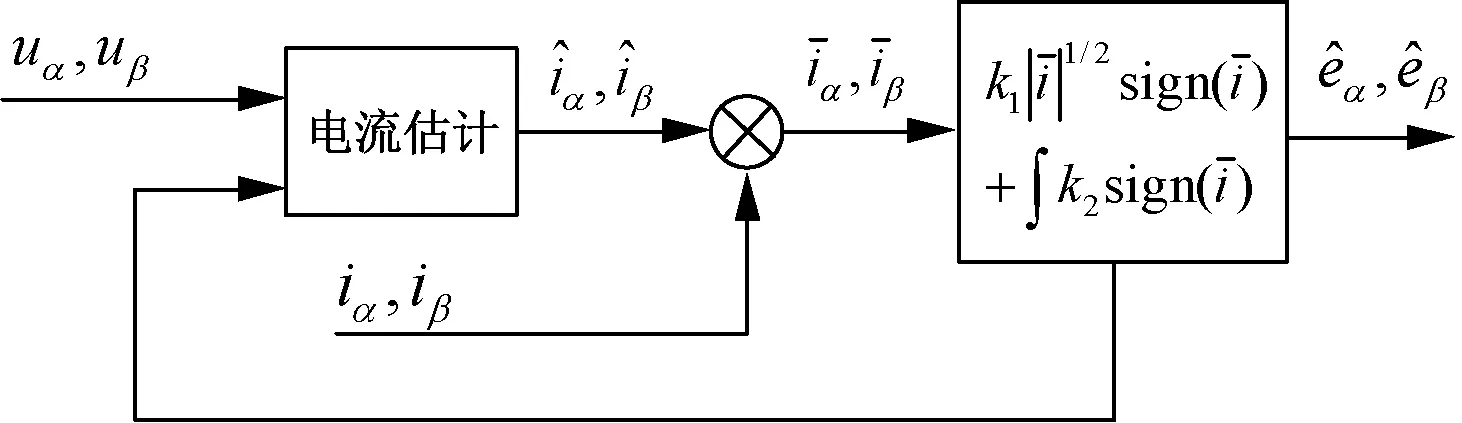
圖4 STO算法結構

仿真電機模型參數如表1所示。

表1 仿真電機參數模型

首先,驗證觀測器的反電動勢觀測性能以及位置和轉速觀測效果,觀測器不參與閉環,實際位置信號由電機模型提供。初始轉速為750 r/min,在1 s時,轉速指令階躍為1 200 r/min。圖5為STO觀測反電動勢波形。圖6為傳統SMO+PLL觀測反電動勢波形。

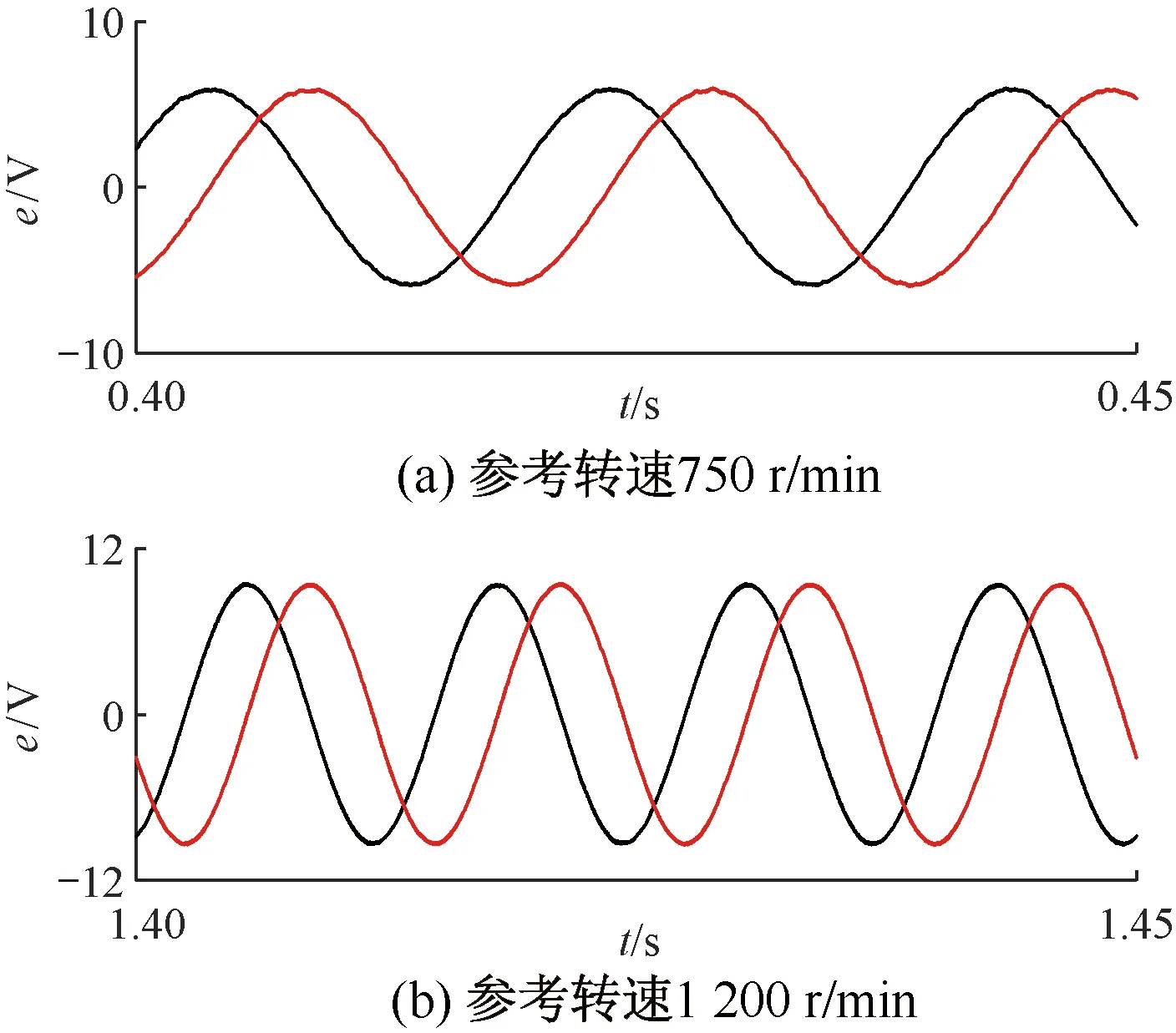
圖5 STO觀測反電動勢仿真

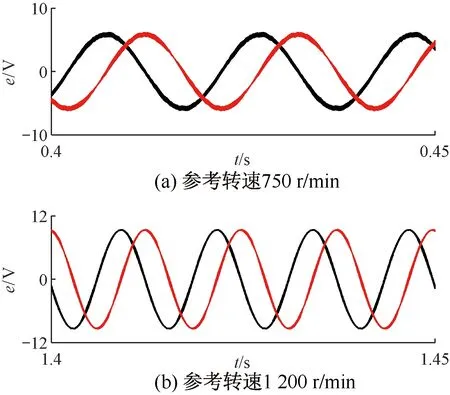
圖6 傳統SMO+PLL觀測反電動勢仿真

圖5和圖6中,在相同濾波參數下,STO觀測反電動勢抖振現象好于傳統SMO+PLL方案,且有更高的正弦度。轉速750 r/min時,前者反電動勢THD為1%,后者為4.1%;轉速1 200 r/min時,前者反電動勢THD為0.74%,后者為2.48%。

圖7和圖8為兩種方案觀測位置與實際位置對比,圖9為兩種方案觀測角度誤差對比。

圖7 STO+PLL轉子位置估計仿真

圖8 傳統SMO+PLL轉子位置估計仿真

圖9 轉子位置誤差仿真對比

圖9中,STO方案位置誤差抖動相對于傳統SMO方案更小。

圖10為兩種方案開環轉速響應曲線。圖11為兩種方案在兩種轉速情況下的對比。

(a)STO

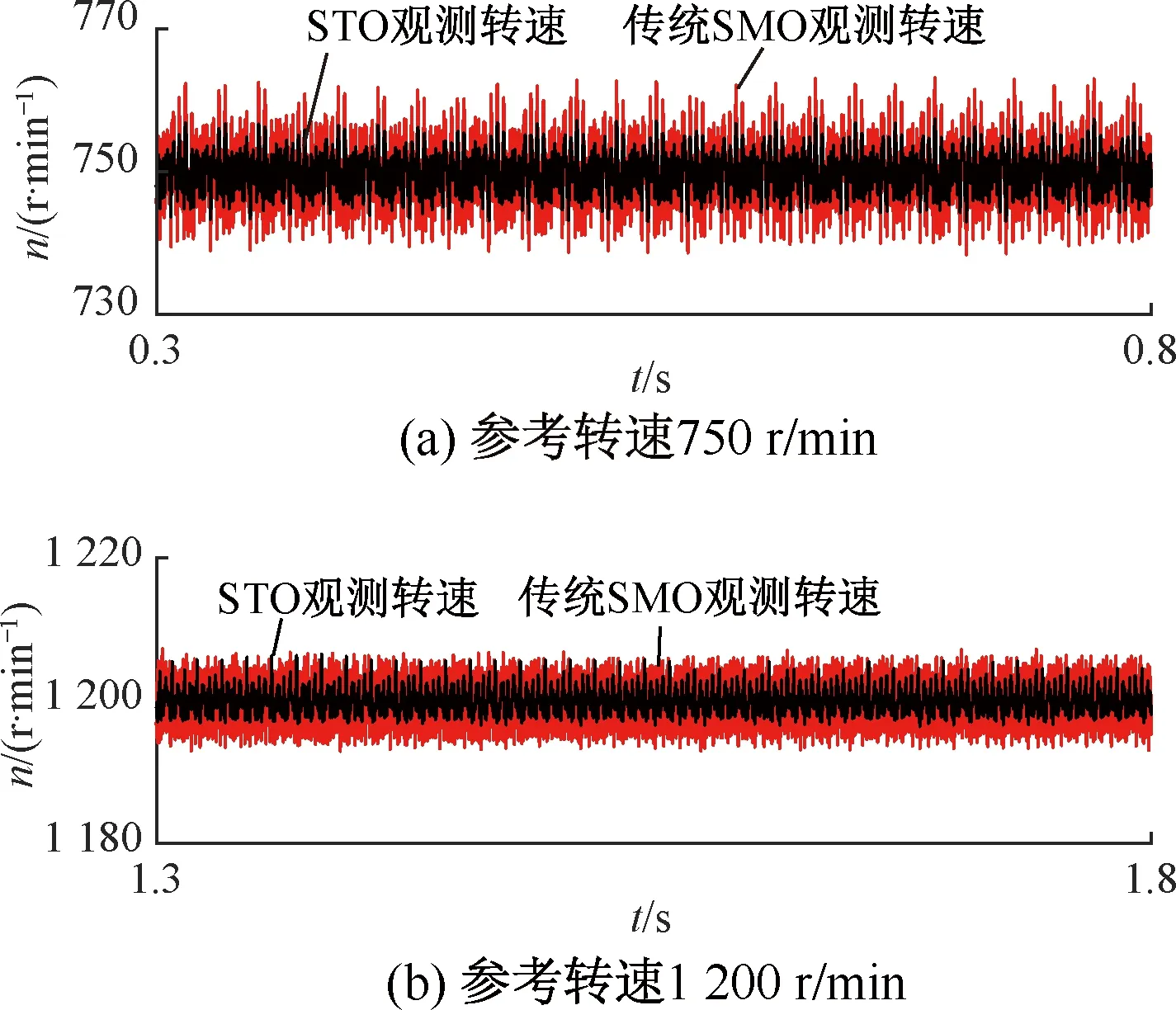
圖11 兩種觀測器觀測轉速對比

圖11中,STO的觀測轉速波動小于傳統SMO+PLL。轉速750 r/min時,前者觀測轉速誤差約為±5 r/min,后者約為±9 r/min;轉速1 200 r/min時,前者觀測轉速誤差約為±4 r/min,后者約為±7 r/min。

在電機1 200 r/min穩定運行時,加0.5 N·m負載,電機的轉速響應曲線如圖12所示。可以看出,觀測器在加載情況下速度跟蹤效果較好。

進行梯形加減速仿真,控制模型改為由觀測器提供的位置和轉速信號閉環。電機初始轉速750 r/min,速度指令在1 s內勻加速至1 200 r/min,后在1 s內勻減速至750 r/min,得到系統的閉環轉速響應曲線如圖13所示。

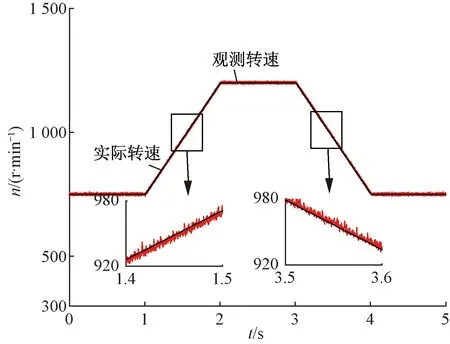
圖13 STO梯形加減速仿真

觀測器全過程觀測效果良好,抗速度擾動能力強。

4.2 實驗分析

實驗硬件平臺如圖14所示。控制器主控芯片使用STM32F446,功率部分采用由三個半橋驅動芯片驅動的三相全橋拓撲,直流電壓24 V。電流環頻率10 kHz,使用霍爾電流傳感器采樣A、C兩相電流。轉子實際位置由編碼器提供。上下位機通訊使用串口協議。

圖14 實驗平臺

首先進行階躍實驗,觀測器不參與閉環。參考轉速由0階躍到750 r/min再到1 200 r/min。圖15為觀測反電動勢波形。圖16為觀測位置與實際位置對比。圖17為轉速響應曲線。

圖15 STO觀測反電動勢實驗波形

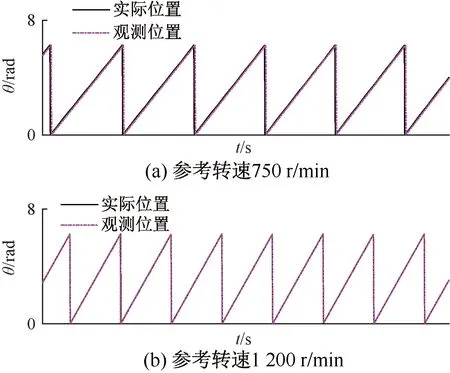
圖16 STO觀測位置與實際位置實驗波形

圖17 STO階躍實驗轉速響應

由圖15可見,反電動勢波形正弦度較好。圖16中,觀測位置與實際位置重合度較高。圖17中,觀測器在中高轉速情況下觀測轉速誤差均較小。

進行加載實驗,觀測器不參與閉環。設置參考轉速為1 200 r/min,在速度穩定后加0.5 N·m負載。圖18為速度響應曲線。從圖18可以看出,觀測器在加載時速度跟蹤效果較好。

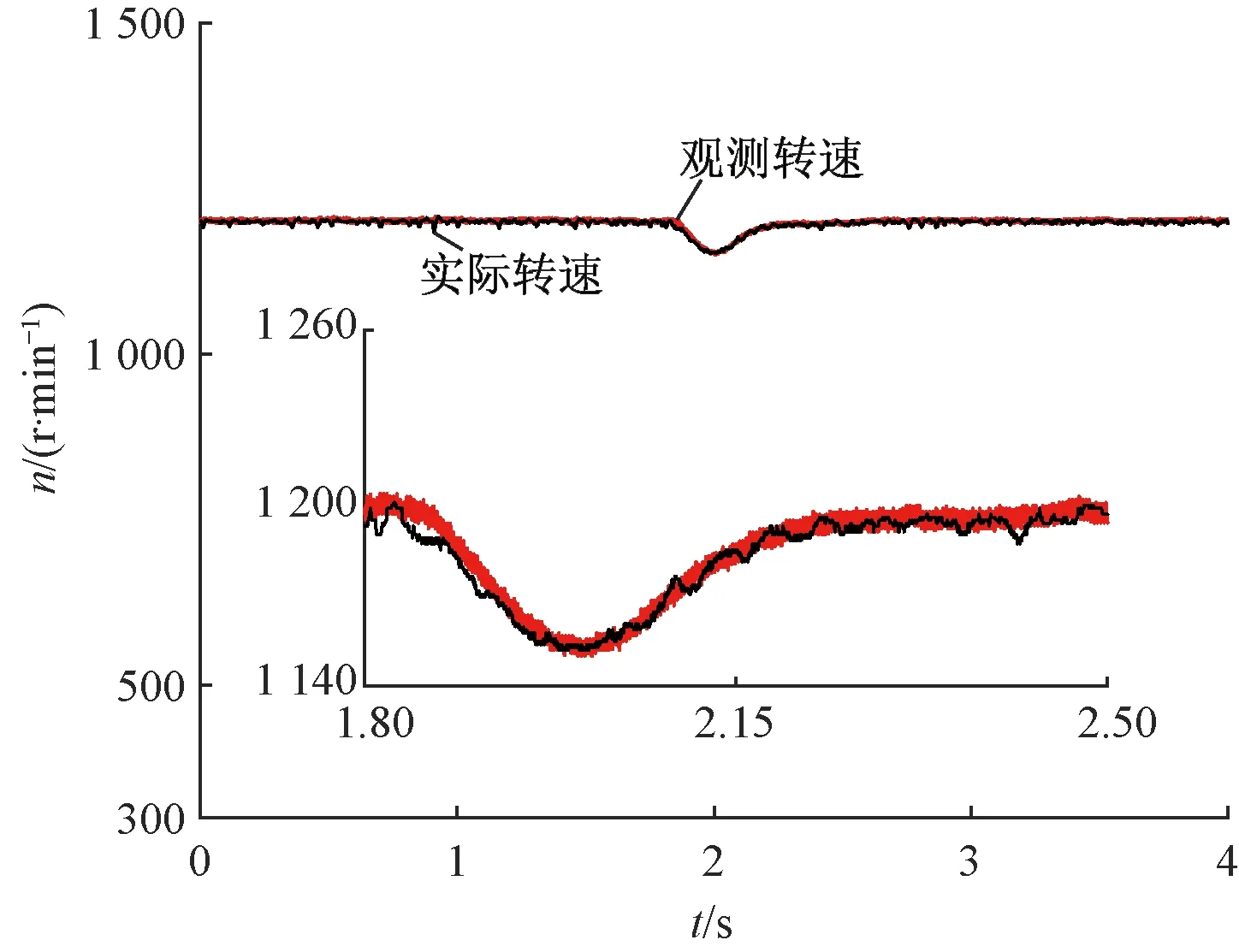
圖18 STO加載實驗

觀測器進行閉環實驗時,系統先在編碼器閉環條件下運行至750 r/min,然后切換到觀測器閉環。經觀測器閉環后,參考轉速首先保持750 r/min,后勻加速至1 200 r/min,后勻減速至750 r/min,其運行效果如圖19所示。

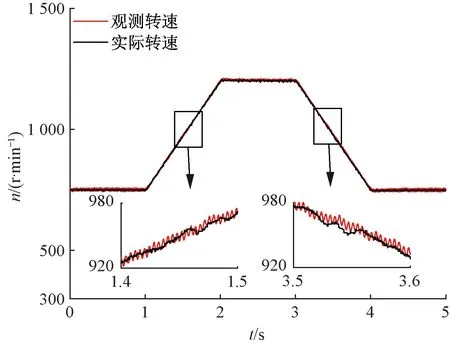
圖19 STO梯形加減速實驗

由圖19可見,STO在電機加減速過程中跟蹤良好。

5 結 語

本文基于超螺旋算法設計SMO,采用PLL得到電機轉子位置并進行自適應補償。仿真和實驗驗證了該觀測器的有效性。本文主要有以下結論:

(1)本文基于超螺旋算法的觀測器相較于傳統SMO觀測反電動勢正弦度更高,觀測位置與觀測轉速抖動更小;

(2)該觀測器有一定的抗外部擾動能力,在負載擾動的情況下表現良好;

(3)觀測器閉環運行效果較好,具有一定的實用應用價值。