RV減速器擺線針齒傳動機構線外嚙入沖擊研究

紀姝婷,李佳林,張躍明

(北京工業大學材料制造學部,100124, 北京)

工業機器人是先進制造業的支撐設備,RV減速器作為工業機器人的核心零部件之一,占整機成本的25%左右,對工業機器人的各項技術指標如傳動精度、壽命、可靠性等均有重要影響[1]。RV減速器有兩級傳動,第一級為漸開線行星齒輪傳動,第二級為擺線針齒傳動。擺線針齒傳動是RV減速器核心傳動機構,對其傳動精度影響較大[2]。

在齒輪傳動中,由于制造誤差、齒廓修形、輪齒變形等原因,實際嚙入點會偏離理論嚙入點,在實際嚙合公法線方向上產生相對速度,引起嚙合沖擊[3]。典型的嚙合沖擊包括嚙入沖擊、節點沖擊和嚙出沖擊,其中嚙入沖擊對傳動性能影響最為顯著[4]。國內外相關學者對機構的嚙入沖擊進行了大量研究。Huang等通過建立直齒圓柱齒輪沖擊模型,研究了瞬態沖擊對齒輪潤滑的影響[5]。周長江等通過對漸開線齒輪線外嚙入機理的研究,提出了求解線外嚙入沖擊力的方法,建立了線外嚙入沖擊摩擦模型[6]。Hu等通過建立行星傳動系統的嚙合沖擊模型,計算出嚙合沖擊點、嚙合沖擊時間和沖擊力,并考慮了載荷作用下各部件偏心誤差和安裝誤差對齒輪嚙合位置的影響[7]。Vedmar等[8]采用有限元方法,計算了齒輪非線性Hertz變形量,提出了直齒輪動態嚙合力計算模型。王峰等闡述了人字齒輪嚙入沖擊位置、速度及沖擊力的推導過程,簡要分析了沖擊力與重合度的關系[9]。張衛青等研究了齒廓修形及重合度對螺旋錐齒輪沖擊力的影響[10]。

在擺線針齒傳動過程中,嚙合力是研究嚙入沖擊過程的基礎。Su等計算了標準擺線輪和修形后的擺線輪與針齒之間的嚙合力[11]。Hsieh研究了擺線針齒的接觸和碰撞條件,以及在傳遞過程中的嚙合力變化,并建立了擺線針齒傳動系統兩種動力學分析模型[12]。Xu等提出擺線針齒傳動的嚙合位置的判定方法,分析了軸承對擺線針齒傳動載荷分布的影響[13]。Zhang等建立了擺線針齒傳動的嚙合力力學模型,并計算出擺線針齒嚙合副間的接觸應力和接觸剛度分布[14]。Yu等研究了擺線針齒嚙合側隙對嚙合力的影響[15]。Ren等通過建立擺線針齒行星傳動的動力學方程,分析了擺線針齒嚙合副的動態嚙合剛度及系統的傳動誤差,探討了擺線針齒嚙合側隙對嚙合力的影響[16]。Blagojevic等利用Solidworks和Matlab軟件,設計了一種新型單級擺線針齒減速器,并建立動力學方程對其進行運動學分析[17]。

雖然針對漸開線齒輪的線外嚙入沖擊較為成熟,但是針對擺線針齒嚙合傳動的線外嚙入沖擊仍有待深入研究。本文對擺線針齒傳動嚙合狀態下的線外嚙入沖擊進行理論分析,揭示線外嚙入沖擊的產生機理,基于H-C(亨特-克羅斯利)接觸碰撞模型和Hertz(赫茲)接觸碰撞變形規律,建立線外嚙入沖擊力學模型,分析擺線輪移距修形和偏心距對沖擊力的影響,這對于減小RV減速器振動和噪聲具有重要意義。

1 擺線針齒傳動線外嚙入點的計算

1.1 擺線針齒線外嚙入沖擊機理

根據擺線針齒傳動的理想嚙合條件,標準的擺線輪與針齒在嚙合公法線上的相對速度為0。在實際嚙合過程中,由于擺線輪修形引起的齒側間隙如圖1(a)所示,以及輪齒受載后的變形如圖1(b)所示,導致擺線輪的實際嚙合點偏離理論嚙合點,并在嚙合公法線產生相對嚙入速度,進而產生嚙入沖擊力。修形后的擺線輪首先克服齒側間隙后,擺線輪與針齒發生接觸碰撞,產生瞬時嚙入沖擊,導致RV減速器產生傳動誤差、振動和噪聲等問題。因此,在探討擺線針齒嚙入沖擊力前,需提出擺線針齒的理論嚙入點與實際嚙入點的計算方法。

(a)修形擺線輪齒側間隙

1.2 理論嚙入點位置

擺線輪修形后,不同擺線針齒嚙合對的齒側間隙大小不一。在擺線輪與針齒初次嚙合時,必須克服擺線輪與針齒的初始間隙,此時擺線輪轉過的一個微小角度即為初始轉角θ0。

圖2為擺線針齒傳動系統的坐標系[18]。固定坐標系Sf與針齒殼固定,移動坐標系Sc與擺線輪固定,θg為擺線針齒傳動機構的輸入角,θ為擺線輪自轉角度。P0為初始節點,P為輸入角為θg的節點。rc、rp分別為擺線輪與針齒的節圓半徑。Oc為擺線輪幾何中心,Op為針齒分布圓幾何中心,Oi為第i個(i≥1)針齒的幾何中心,針齒齒號順時針遞增,POi為第i個待嚙合齒廓對的嚙合公法線。

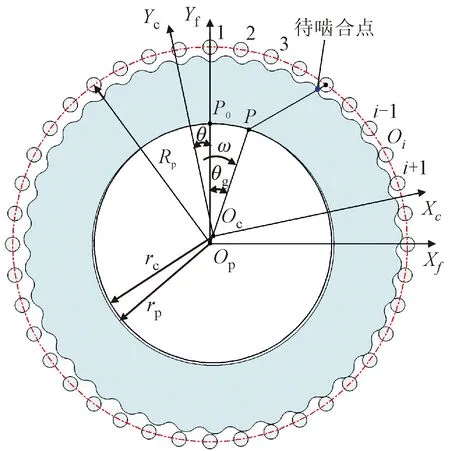
圖2 擺線針齒傳動系統坐標圖Fig.2 The coordinate of cycloid-pin gear drive system

修形擺線輪齒廓方程如下所示

(1)

式中:Rp為針齒分布圓半徑;ΔRp為移距修形量;Δr為等距修形量;a為偏心距;r為針齒半徑;zc為擺線輪齒數;km=azp/(Rp+ΔRp)為短幅系數,zp為針齒齒數。

擺線輪轉動角度為θg,Sc到Sf的坐標變換矩陣為

(2)

則擺線輪在坐標系Sf下的齒廓方程為

rf=Mfcrc

(3)

在坐標系Sf中,第i個針齒的幾何中心坐標為

(4)

在坐標系Sf中,節點P的幾何中心坐標為

(5)

第i個嚙合對公法線的方程為

(6)

式中:(xci,yci)為擺線輪待嚙合點坐標。

定義齒側間隙為嚙合公法線上針齒齒廓與擺線輪齒廓的距離di,則di求解公式為

(7)

將式(4)～(6)代入式(7),通過Python編程迭代計算,可得出初始轉角θ0與各嚙合對待嚙合點的坐標。

1.3 實際嚙入點位置

實際的擺線針齒嚙合過程中,擺線輪先克服齒側間隙與針齒發生接觸,進而產生壓縮變形,擺線輪轉動β,見圖3。A點為擺線輪理論嚙合點,產生壓縮變形后,擺線輪A點(x1,y1)轉到B點(x2,y2)位置,則彈性扭轉角β為

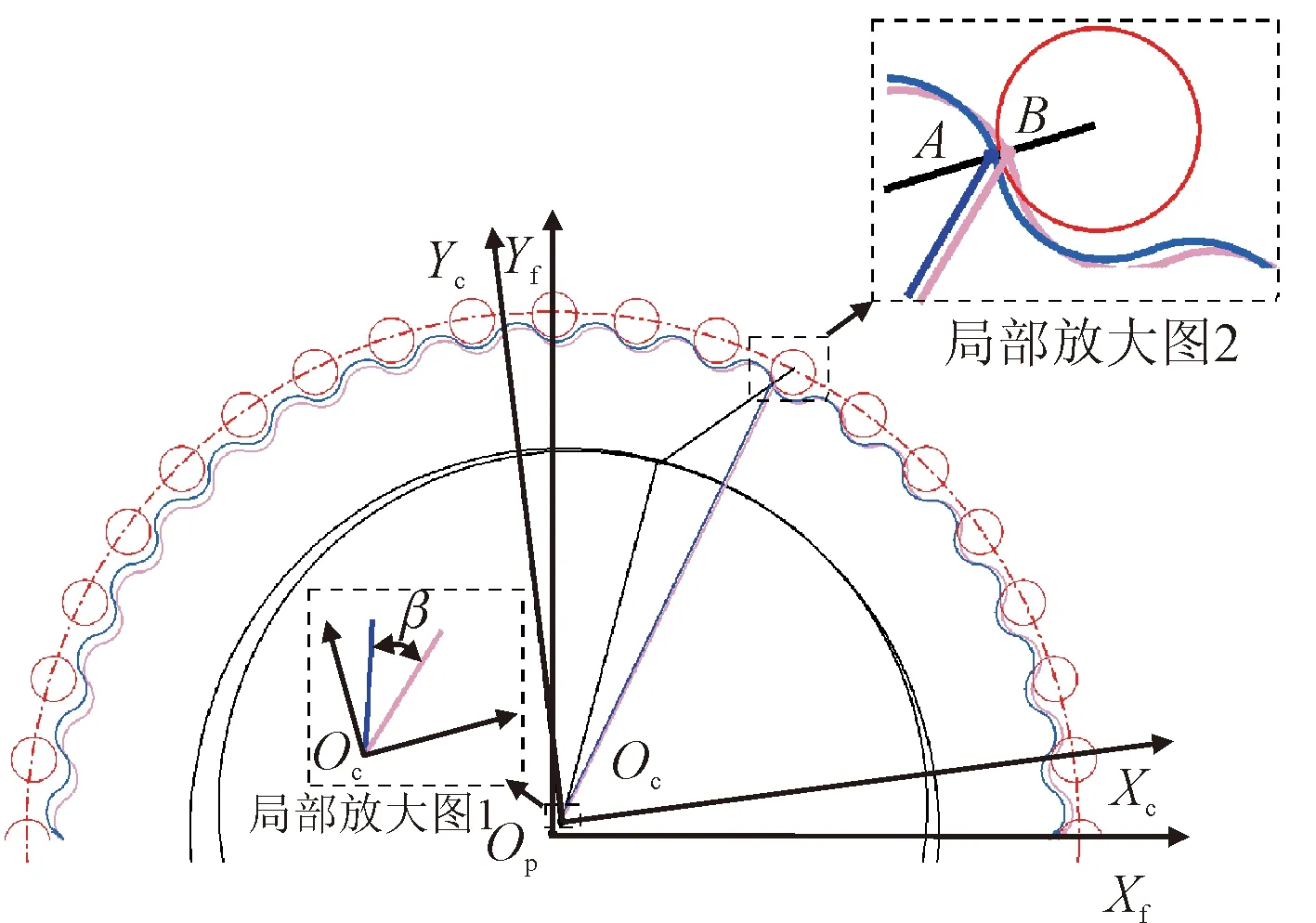
圖3 擺線輪彈性扭轉角βFig.3 The elastic torsion angle β of cycloid gear

(8)

擺線輪與針齒嚙合時,如圖4所示,擺線輪與針齒在嚙合公法線方向壓縮量δi計算公式為

圖4 擺線輪和針齒的接觸形變量與力臂關系Fig.4 The relationship between contact deformation of cycloid gear and pin gear and force arm

δi=βli

(9)

式中:li為嚙合力力臂。

設受力最大的一對擺線輪與針齒接觸變形量為δmax,其嚙合點公法線到擺線輪中心點的距離為lmax,由此可得

(10)

式中:lmax=rc。

擺線輪與針齒之間的接觸可簡化為兩圓柱體接觸,根據赫茲接觸變形公式[19],擺線輪與針齒的最大接觸變形δmax計算公式為

(11)

式中:B為擺線輪厚度;μ1、μ2為擺線輪與針齒材料的泊松比;E1、E2為擺線輪與針齒的彈性模量;ρc為擺線輪齒廓曲率半徑;b為擺線針齒接觸半寬;Fmax為最大初始嚙合力。

接觸半寬推導公式為

(12)

式中:ρ*為擺線針齒綜合曲率半徑;ED為擺線針齒綜合彈性模量。

擺線針齒接觸的綜合齒廓曲率半徑ρ*[20]為

(13)

擺線針齒接觸綜合彈性模量ED為

(14)

擺線輪齒廓曲率半徑為

(r+Δr)

(15)

將式(11)代入式(10),則β計算公式為

(16)

由式(16)可知,要求得β需計算最大初始嚙合力Fmax。擺線針齒傳動機構中第i對嚙合齒的嚙合力Fi與Fmax關系為

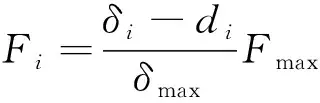
(17)

由于初始間隙的存在,只有部分齒廓對參與嚙合,假設只有m到n號針齒接觸,根據轉矩平衡原理可得

(18)

最大初始嚙合力計算公式為

(19)

式中:T為輸出軸上作用的扭矩;Tc為單個擺線輪傳遞的扭矩。

暫取標準擺線輪與針齒之間的最大嚙合力作為最大初始嚙合力

(20)

由于在計算時將標準擺線輪與針齒之間的最大嚙合力Fmax0作為最大初始嚙合力Fmax,所計算得出的結果并不準確[21]。因此,采用逐次迭代的方法,判斷求解得到的Fmax與最大初始嚙合力Fmax0是否滿足|Fmax-Fmax0|≤0.1%Fmax,如果不滿足條件,則將Fmax的值賦予Fmax0代入式(11)～(19)中重新進行計算,直到滿足上述條件,此時Fmax=Fmax0。計算流程如圖5所示。在求得Fmax的準確值后,代入式(16)求得β。將β代入式(8),可求得擺線針齒傳動的實際嚙入點坐標。

圖5 最大初始嚙合力Fmax計算流程圖Fig.5 Calculation flow chart of maximum initial engagement force Fmax

2 線外嚙入沖擊力計算

忽略軸承、曲軸等零件的變形影響,將擺線輪與針齒的嚙入沖擊簡化為沿嚙合公法線方向的彈性碰撞行為,兩剛體接觸碰撞力即為線外嚙入沖擊力。

2.1 線外嚙入沖擊速度

由于存在制造誤差、彈性變形和齒側間隙,導致擺線輪與針齒在公法線方向產生相對速度。沿嚙合公法線方向的相對嚙入速度為嚙入沖擊速度,如圖6所示。圖中P為擺線輪節點,M為擺線輪實際待嚙合點,PM為擺線針齒實際嚙合公法線,Vp為擺線輪M點處瞬時公轉速度,Vc為擺線齒M點處的自轉速度,V為擺線齒M點沿實際嚙合公法線速度,則線外嚙入沖擊速度計算過程如下

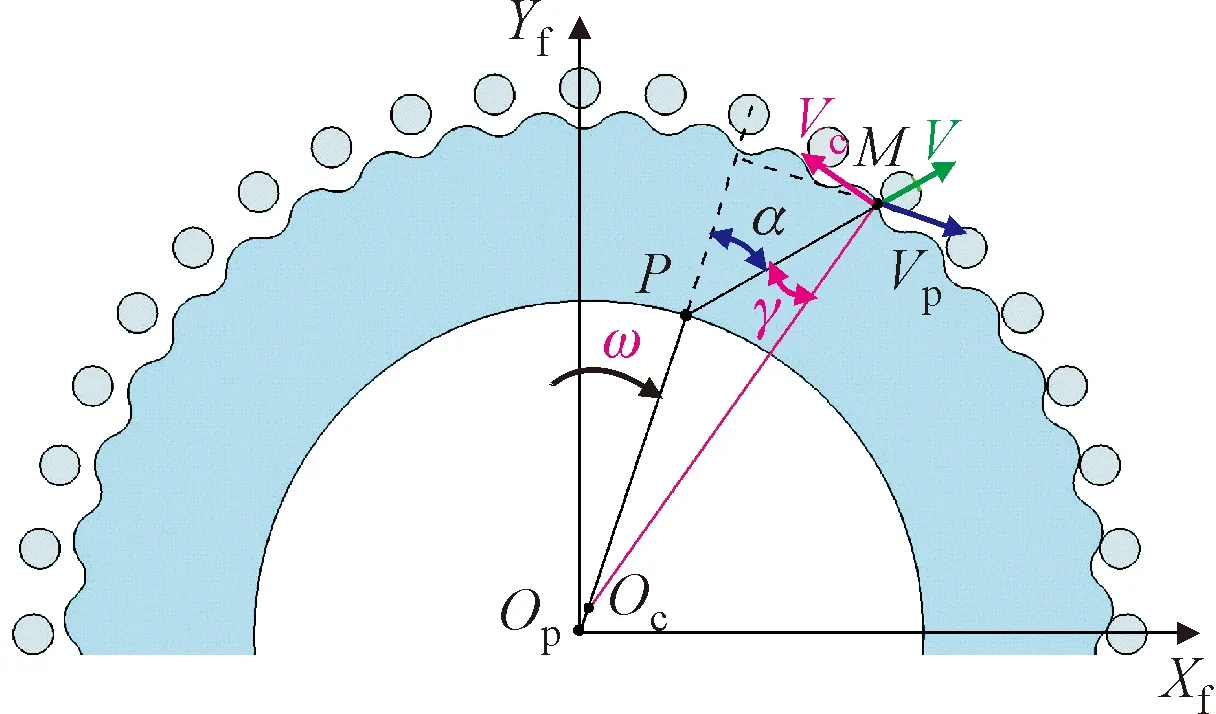
圖6 擺線針齒相對嚙入速度Fig.6 Relative velocity of meshing-in of cycloid-pin gear

Vp=ω×OpOc

(21)

(22)

|V|=|Vp|sinα-|Vc|sinγ

(23)

式中:ω為擺線輪公轉角速度;α為嚙合公法線PM與OpP的夾角;γ為嚙合公法線PM與OcM的夾角;iH為擺線針齒傳動比。

2.2 線外嚙入沖擊力模型

根據經典力學碰撞理論,彈性碰撞過程分為壓縮和恢復兩個階段,由壓縮變形引起的位移,是嚙入沖擊總位移的主要部分。當兩剛體發生碰撞剛體達到最大壓縮形變時,所對應的力即為最大沖擊力。將擺線輪與針齒的嚙入沖擊過程等效為兩圓柱體的非線性接觸碰撞動力學行為,最大接觸碰撞力即為最大沖擊力。

圖7為Hertz接觸碰撞變形規律。首先兩碰撞物體產生壓縮變形,變形到最大位置δmax后,此時對應的力為最大沖擊力FSmax,進而逐漸恢復初始狀態。

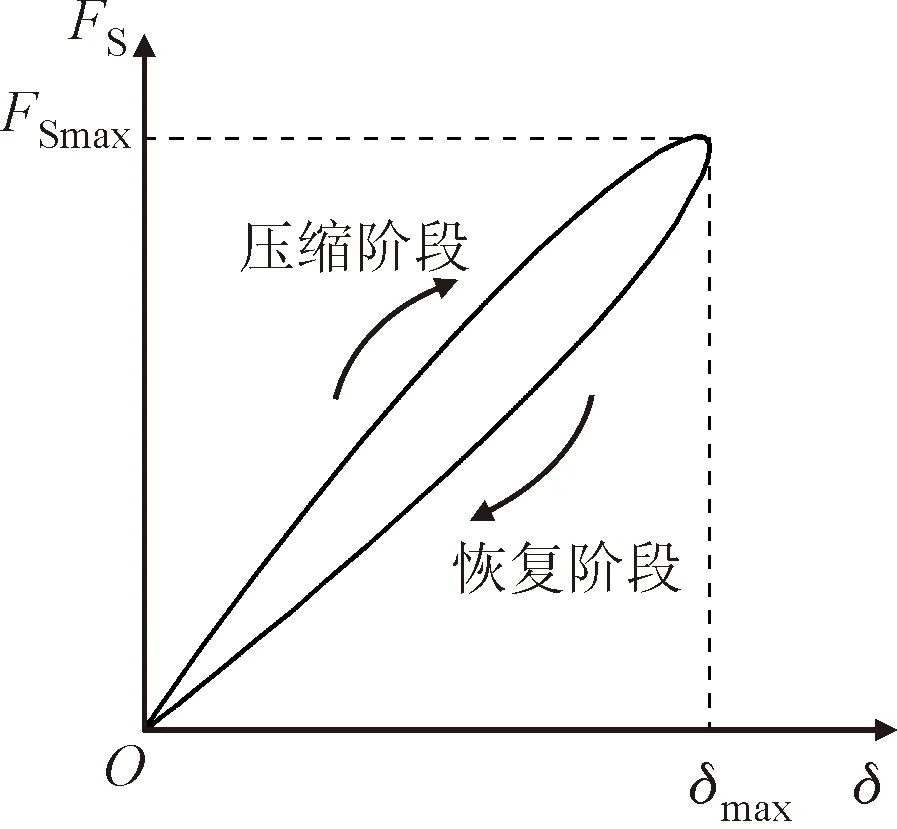
圖7 Hertz接觸碰撞變形曲線Fig.7 The curve of Hertz contact collision deformation

基于H-C非線性接觸碰撞模型[22],建立適用于擺線針齒傳動嚙入沖擊的力學模型,其表達式為

(24)

C(δ)的計算公式為

C(δ)=χδn

(25)

2.2.1 非線性接觸力模型

擺線輪與針齒產生壓縮變形后,接觸區域寬度為2b,長度為B[23],如圖8所示,由Hertz公式可得

圖8 擺線針齒等效接觸模型Fig.8 The equivalent contact model of cycloid-pin gear

(26)

假設擺線輪與針齒的彈性模量與泊松比相同,令E1=E2=E,,μ1=μ2=μ,化簡式(26),可得

(27)

由圖8幾何關系可知

(28)

式中:δc為擺線齒形變量。

將式(28)代入式(27),整理可得擺線齒接觸變形量與接觸力的關系為

(29)

2.2.2 非線性阻尼力模型

考慮接觸碰撞過程中,阻尼力作用的部分能量以熱量形式散失,接觸碰撞過程中動能損失為

(30)

根據動量定理

(31)

根據牛頓運動學定義,兩個物體碰撞后的恢復系數cr可定義為碰撞后的相對速度比碰撞前的相對速度,表達式[24]為

(32)

因此,將式(31)和(32)代入式(30),發生沖擊后,損失動能為

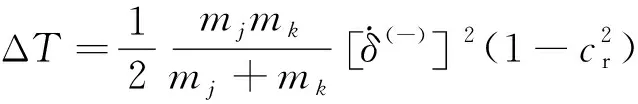
(33)

在壓縮階段,由阻尼力損耗的能量可表達[25]為

(34)

式中:ΔEc為壓縮階段消耗能量。

對式(34)進行變量替換,根據三角函數積分性質,可得

(35)

將式(34)代入式(35),則壓縮過程中遲滯阻尼損耗能量可表示為

(36)

根據能量守恒定律,擺線輪與針齒發生沖擊后,碰撞初始時刻能量T(-)轉化為3部分:一部分為擺線輪與針齒繼續運動的動能Ts,第二部分為最大彈性勢能Umax,最后一部分為滯后阻尼作用轉化的熱能ΔEc,即

T(-)=Ts+Umax+ΔEc

(37)

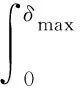
(38)

為判斷非線性接觸力影響因素,由式(29)可知,令S為非線性變形系數,則擺線輪與針齒接觸力可表示為

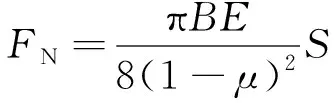
(39)

其中S為

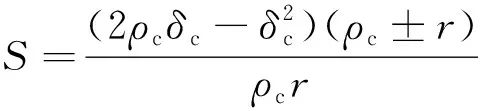
(40)

根據式(40)分析可知,擺線輪形變量δc、偏心距a和移距修形量ΔRp對擺線針齒非線性接觸力影響較大。同時,為了確定阻尼力形變量貢獻系數n, 采用多變量擬合方法,構建偏心距、擺線輪移距修形量和形變量與S之間的映射關系。設S為

(41)

式中:ε1～ε4為擬合系數。因此可根據式(41)確定最大彈性勢能Umax和遲滯阻尼系數χ的表達式。

將式(41)代入式(38),則最大勢能Umax可表示為

(42)

根據壓縮過程的動量守恒,則有

(43)

考慮擺線輪與針齒沖擊過程中會產生能量損失時,則式(37)可表達為

(44)

將式(36)、式(45)～(48)代入式(44),經推導可得阻尼影響因子χ表達式為

(45)

聯立式(24)、(45),最終可得到擺線針齒傳動沖擊力模型為

FS=

(46)

忽略重力作用,根據Hertz接觸變形理論,彈性體動能的損失即為碰撞力所消耗的能量,則彈性體損失動能、變形量、沖擊力有如下關系

(47)

(48)

(49)

式中

A1=m

3 沖擊力模型驗證

現以RV-20E樣機為研究對象,樣機數據如表1所示。

表1 RV-20E的參數和材料屬性

3.1 線外嚙入沖擊力理論計算

經計算,圖9所示為擺線輪轉過初始轉角0.6°后的齒側間隙分布。此時6號針齒對應的嚙合對嚙合,7號針齒嚙合對存在齒側間隙。空載狀況下,擺線輪公轉1 ms后,擺線輪7號齒與針齒處于嚙合狀態,如圖10所示。

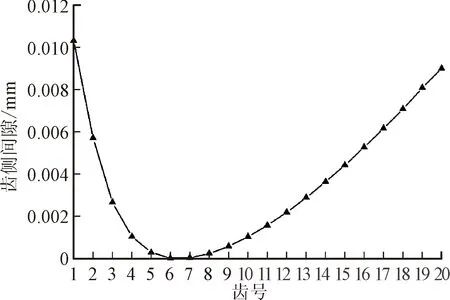
圖9 擺線針齒初始間隙Fig.9 The initial clearance of cycloid pin teeth

圖10 擺線輪公轉1 ms后齒側間隙Fig.10 The clearance after cycloid gear revolution of 1 ms

假設偏心距a設計范圍為0.99～1.01 mm,接觸變形量δc變化范圍為0～0.01 mm,移距修形量的修形范圍為-0.05～0.05 mm,代入式(41)后,通過Matlab進行多變量擬合,可得到S的擬合公式為

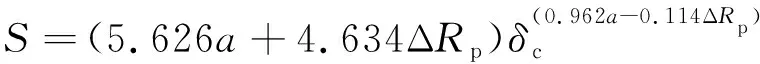
(50)

表2為擬合精度相關參數,可見擬合精度較好。

表2 變形系數S擬合相關數據

圖11為擺線針齒傳動的線外嚙入沖擊力隨時間變化情況。由圖可知,在0～6.95 μs時間段,擺線輪與針齒未發生沖擊,此時沖擊力為0。在克服間隙后,擺線輪在6.95 μs處與7號針齒發生沖擊,隨后短時間內沖擊力迅速增加到峰值132.5 N。

圖11 理論沖擊力隨時間變化曲線Fig.11 The change curve of theoretical impact force with time

3.2 有限元仿真

3.2.1 有限元仿真設置

將擺線針齒傳動機構導入瞬態動力學模塊后,在Space Claim軟件中設置連接關系,設置材料類型,對擺線針齒進行局部精密網格劃分,如圖12所示。仿真時間為1 ms,為更直觀觀察擺線輪沖擊力變化,提取7號針齒對應的嚙合對接觸面中心點的沖擊力數據。

圖12 擺線針齒局部精密網格劃分Fig.12 The local precision grid generation of cycloid-pin gear

3.2.2 仿真結果分析

擺線輪7號齒的沖擊力隨時間變化結果如圖13所示,0～11.8 μs時擺線輪克服初始間隙未與針齒發生碰撞,此期間沖擊力為0。在11.8 μs與7號針齒發生碰撞,沖擊力在短時間內瞬時增加到122.7 N。

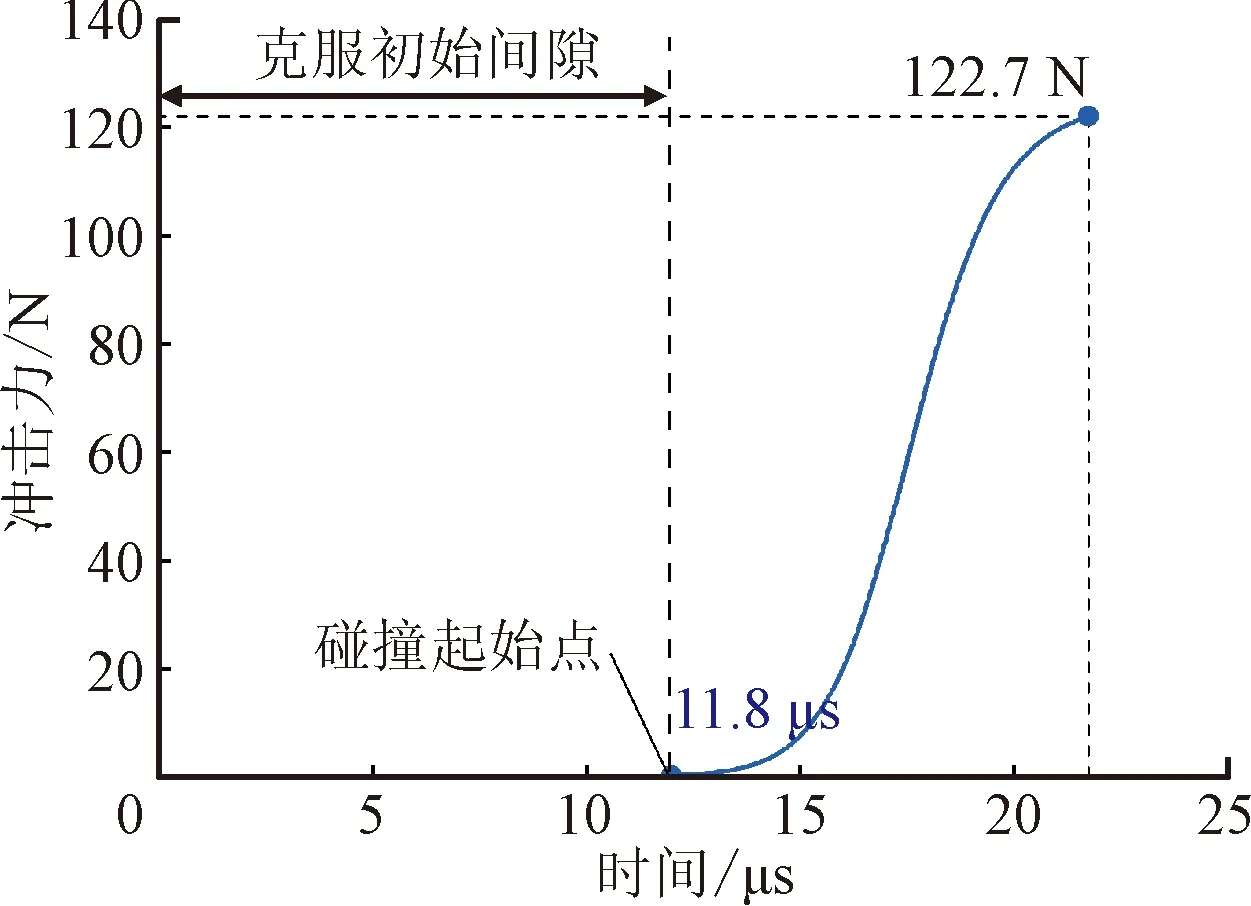
圖13 沖擊力隨時間變化仿真結果Fig.13 The simulation results of impact force changing with time

3.3 沖擊力模型理論結果與仿真結果對比

擺線針齒嚙入沖擊理論計算結果與Ansys有限元仿真結果對比如圖14所示,理論計算得到的擺線輪克服初始間隙時間相對于仿真得到的時間短,該現象是由于初始沖擊時間的選取差異所造成的。理論上的最大沖擊力為132.5 N,仿真得到的最大沖擊力為122.7 N,誤差率為7.98%,計算誤差在允許范圍內,因此有限元仿真結果驗證了線外嚙入沖擊力模型可行性。

圖14 理論沖擊力與仿真沖擊力對比圖Fig.14 The comparison of theoretical impact force with simulation impact force

4 不同碰撞參數對沖擊力的影響

4.1 移距修形對沖擊力影響

沖擊力隨移距修形量ΔRp變化規律如圖15所示。在等距修形量一定時,當修形量在-0.05～0.05 mm取值范圍內,對于負移距修形,修形量越大,嚙入沖擊力越小;對于正移距修形,修形量越大,嚙入沖擊力越大。移距修形對克服初始間隙時間影響較大,這是由于不同修形方式與修形量對擺線針齒齒側間隙影響較大。移距修形量對沖擊持續時間影響并不大。

圖15 移距修形對最大沖擊力的影響Fig.15 The influence of radial-moving modification eccentricity on maximum impact force

4.2 偏心距設計參數對沖擊力的影響

沖擊力隨偏心距a變化規律如圖16所示。當偏心距在0.99～1.01 mm設計范圍內,偏心距a越小,擺線針齒的線外嚙入沖擊力越大,擺線針齒齒側間隙減小從而使克服初始間隙時長縮短,但對沖擊持續時間影響不大。

圖16 偏心距對最大沖擊力的影響Fig.16 The influence of eccentricity on maximum impact force

5 結 論

(1)基于擺線針齒嚙合理論,闡述了擺線針齒傳動線外嚙入沖擊產生機理,提出了擺線輪與針齒實際嚙入點坐標計算方法,提出了線外嚙入沖擊速度計算模型,為沖擊力學模型建立提供基礎。

(2)基于H-C接觸碰撞模型和Hertz接觸碰撞變形規律,建立了擺線輪與針齒沖擊力模型。考慮初始間隙,通過數值算法,揭示了線外嚙入沖擊力隨時間的變化規律。

(3)采用Ansys Workbench軟件對擺線針齒嚙入沖擊力進行計算。仿真分析結果與理論計算結果差異較小,證明了線外嚙入沖擊模型的準確性。

(4)分析偏心距和移距修形量對擺線針齒嚙入沖擊力影響。最終得出偏心距越小,擺線針齒嚙入沖擊力越大;等距修形量一定時,正移距修形量越大,擺線針齒嚙入沖擊力越大,負移距修形量越小,擺線針齒嚙入沖擊力越大的結論。