大跨斜拉橋基于索力的結構損傷識別研究

于 虹

（1.中鐵第四勘察設計院集團有限公司,湖北 武漢 430063; 2.中國鐵建股份有限公司橋梁工程實驗室,湖北 武漢 430063）

0 引言

斜拉橋在服役過程中，由于荷載作用、材料老化和環境因素的作用，會出現拉索銹蝕、主梁及主塔開裂、螺栓松動等病害，造成結構性能退化[1]。因此，及時對斜拉橋結構的損傷進行檢測和修復，對保障橋梁結構的安全服役具有重要意義[2-3]。

斜拉索是斜拉橋的主要承重構件之一，其受力狀態是衡量斜拉橋是否處于正常狀態的重要參量。斜拉橋結構主梁損傷會引起恒載內力重分布，從而引起斜拉索索力變化，因此可以利用斜拉索索力變化識別斜拉橋主梁損傷。孫宗光[4]首次探討了基于斜拉索張力指標與人工神經網絡技術相結合，對斜拉橋主梁中的損傷進行定位識別。朱浩等[5]根據斜拉橋主梁的線形由于斜拉索索力的改變而改變這一規律，通過對主梁位移的改變量進行反演，得到索力的變化情況，從而對斜拉橋的內力狀態進行識別。Hua[6]利用斜拉橋主梁損傷前后的索力變化，通過構造斜拉橋主梁參數對斜拉索索力的靈敏度矩陣，結合模型修正技術對斜拉橋的主梁進行損傷識別。李延強等[7]基于斜拉橋主梁損傷對索力的敏感性分析，選擇一組四根（空間位置對稱）對主梁損傷最敏感的斜拉索索力構造損傷指標，利用BP 神經網絡對斜拉橋有限元模型中的主梁損傷進行識別。

該文利用斜拉索索力作為損傷敏感指標，并分析計算斜拉索索力對結構損傷的靈敏度，據此對高速鐵路大跨度斜拉橋結構中的損傷進行識別分析。以裕溪河特大橋為研究對象，對所提出方法的有效性和準確性進行驗證。

1 斜拉索索力對主梁損傷靈敏度分析

1.1 靈敏度分析理論

靈敏度分析主要是研究系統輸入x的變化會導致系統響應量g如何變化的問題。當系統的輸入發生變化時，系統的響應量也將會隨之發生改變，這種改變的相對程度就稱為系統響應量g對于系統輸入變量x的靈敏度，可以用偏微分?g/x? 表示。

有限差分法的原理是利用差商近似微商，可以表示為

1.2 斜拉索索力對主梁損傷靈敏度計算

在結構損傷識別研究中，通常假設結構的質量在損傷發生時不發生變化，通過結構單元剛度的變化來模擬結構損傷。假設斜拉橋結構主梁第j個單元的剛度參數（如抗彎剛度）由折減至損傷狀態的，則第j個單元的剛度折減系數(Stiffness Reduction Factor，SRF)可以定義為

式中，ne——斜拉橋結構主梁中單元的個數。剛度折減系數jγ的取值范圍為-1~0。

該文通過折減有限元模型中結構單元的彈性模量，實現對結構損傷的模擬。利用MATLAB 調用ANSYS，計算斜拉索索力對斜拉橋主梁損傷的靈敏度矩陣，具體步驟如下：

（1）計算健康狀態下裕溪河特大橋在恒載作用下的斜拉索索力向量F0。

（2）保持其他參數不變，利用MATLAB 調用ANSYS，依次令第j個主梁結構單元發生1%剛度折減（γj=-0.01），計算此時恒載作用下的斜拉索索力向量。

（3）基于有限差分理論，利用公式（1）計算斜拉索索力對第j個主梁結構單元損傷的靈敏度。

（4）重復步驟（2）和（3），計算斜拉索索力對所有主梁結構單元損傷的靈敏度，得到斜拉索索力對主梁損傷的靈敏度矩陣。

2 基于斜拉索索力的損傷識別方程

基于斜拉索索力變化的損傷識別方程可以表示為

式中，[S]——斜拉索索力對結構損傷的靈敏度矩陣；{FD}——通過測量得到的結構損傷狀態的斜拉索索力；{F0}——通過測量得到的未損傷狀態的斜拉索索力。解向量γ中的非零元素對應的單元編號反映損傷的位置，非零元素的大小反映損傷的程度。

3 基于稀疏正則化的結構損傷識別

在實際工程中，通過測量獲取的斜拉索索力向量中元素的個數通常要遠小于未知結構單元剛度參數的個數。因此，公式（3）通常為欠定方程組，有無窮多個可能的解，不滿足適定性問題解的唯一性，即公式（3）的求解是一種不適定問題。正則化算法是求解不適定問題的有效方法，它利用具體問題的某些附加信息，通過一個近似的適定性問題去尋找原不適定問題的近似解。稀疏正則化是指在優化問題的求解過程中，將l1范數引入目標函數，使解向量具有稀疏性。

結構損傷通常只發生在整個結構的一小部分構件中，即損傷向量具有稀疏性。基于這個先驗知識，可以在公式（3）的求解過程中引入對解向量γ的稀疏約束，將公式（3）轉換為一種約束優化問題P1：

問題P1等價于如下的稀疏正則化問題：

式中，J——稀疏正則化問題的目標函數；τ——正則化參數。

對于稀疏正則化問題，當正則化參數的取值達到一定限值時，問題的解收斂于零，即解中元素全為零。正則化參數τ的最大值可以表示為

該研究提出的大跨斜拉橋基于索力的結構損傷識別流程如圖1 所示。首先，選取斜拉索的索力作為損傷敏感指標，并利用有限差分法計算斜拉索索力對結構損傷的靈敏度；然后，建立一個由結構剛度折減系數和損傷前后斜拉索索力組成的欠定方程組；最后，使用稀疏正則化算法對欠定方程組進行求解，解向量中的非零元素表示結構損傷的位置和程度。

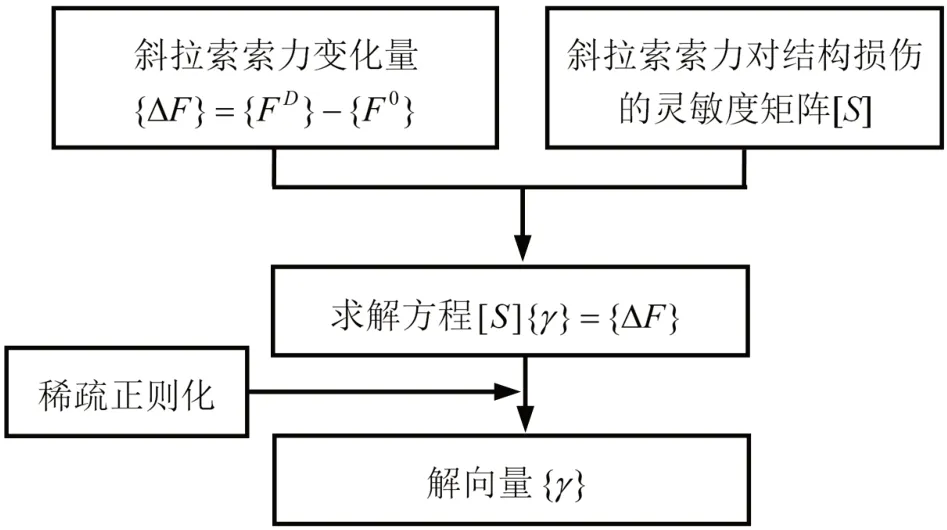
圖1 大跨斜拉橋基于索力的結構損傷識別流程

4 數值模擬算例

4.1 裕溪河特大橋簡介

商丘至合肥至杭州鐵路裕溪河特大橋主橋采用（61+120+324+120+61）m 雙塔鋼箱桁梁斜拉橋方案，全長686 m。以裕溪河特大橋為研究對象，對所提出損傷識別方法的精度和有效性進行驗證。裕溪河特大橋全橋立面布置如圖2 所示。

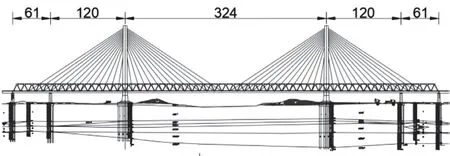
圖2 裕溪河特大橋全橋立面布置示意圖（m）

大橋主梁為鋼箱桁結構，桁架采用不帶豎桿的華倫式桁架，下弦采用整體式鋼箱梁，如圖3 所示。

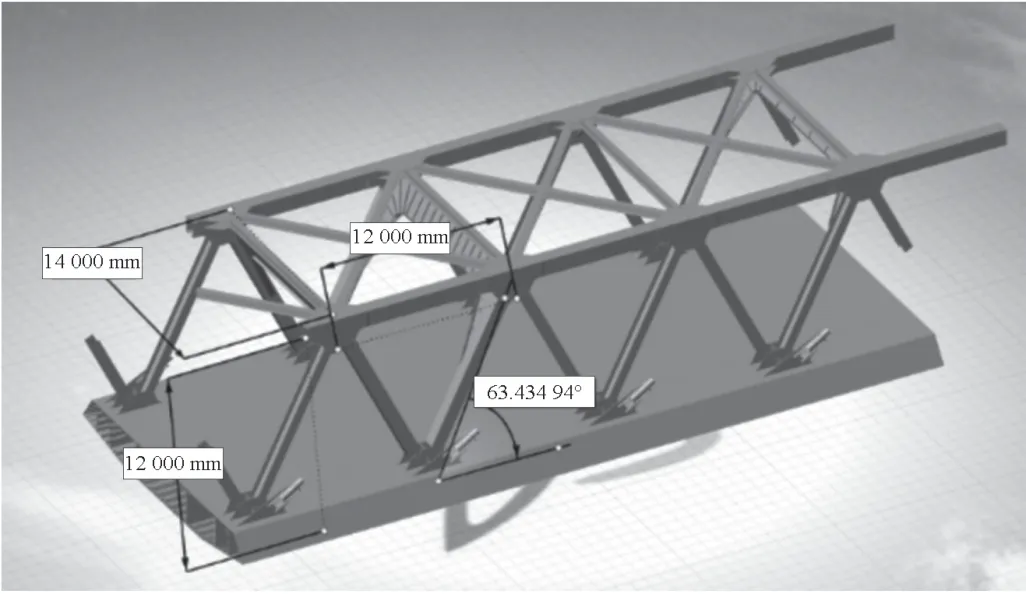
圖3 裕溪河特大橋主梁結構示意圖

4.2 斜拉索索力對主梁損傷靈敏度矩陣

裕溪河特大橋主梁為組合鋼箱桁梁，該文以箱梁發生損傷的情況為例，對基于索力的大跨斜拉橋結構損傷識別過程進行說明。裕溪河特大橋斜拉索為空間雙索面，立面上每塔兩側共13 對索，全橋共104 根斜拉索。對每根斜拉索單獨進行編號，如圖4 所示。按照在商丘至杭州方向線路中心線的左側或右側，將全橋斜拉索分為左側索面和右側索面。對于左側索面，斜拉索自商丘至杭州方向依次編號為1~52；對于右側索面，斜拉索自商丘至杭州方向依次編號為53~104。

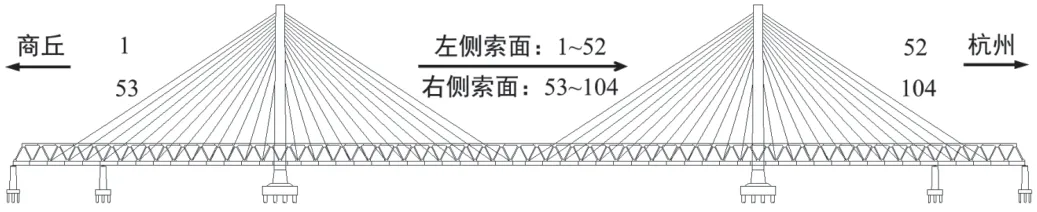
圖4 裕溪河特大橋斜拉索編號簡圖

將裕溪河大橋主梁箱梁按照節間劃分為57 個梁段，對每個梁段單獨進行編號，自商丘至杭州方向依次編號為1~57，如圖5 所示。

圖5 裕溪河特大橋箱梁編號簡圖

將箱梁的每一個梁段看作一個損傷位置，依次計算每一個梁段發生1%剛度折減時的斜拉索索力，基于有限差分理論可以得到斜拉索索力對箱梁損傷的靈敏度矩陣，如圖6 所示（為方便展示，取絕對值）。

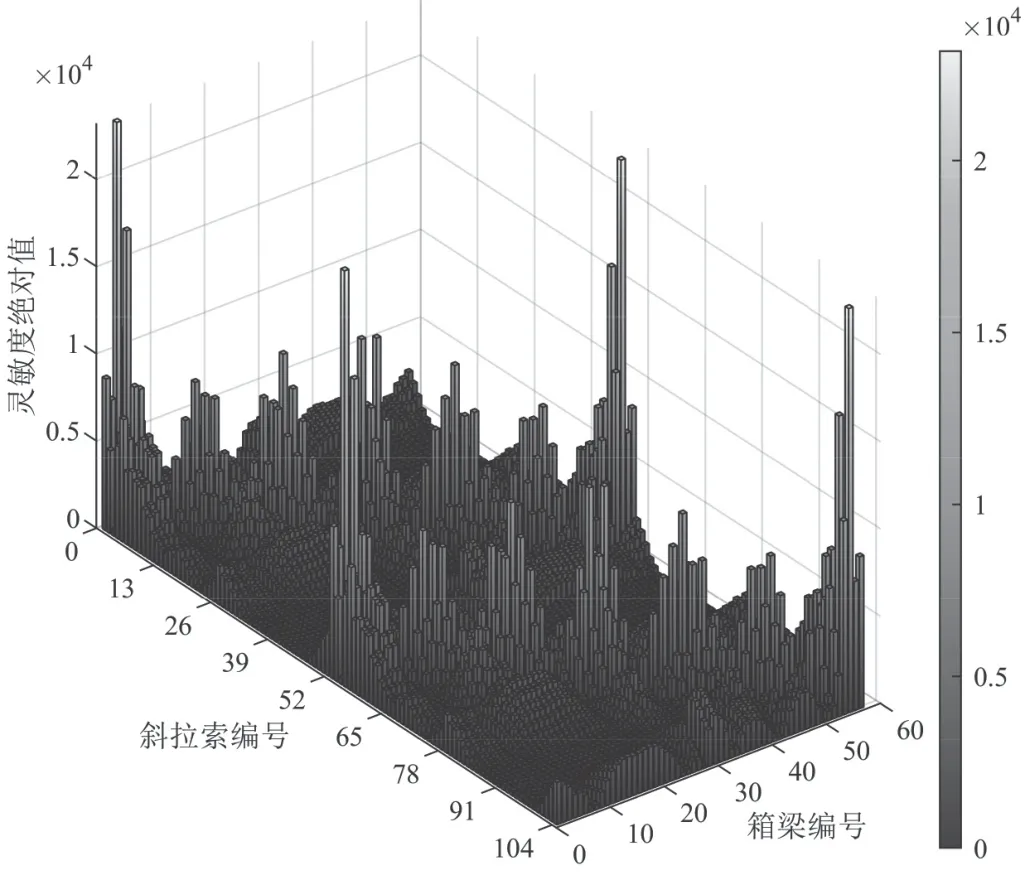
圖6 斜拉索索力對箱梁損傷的靈敏度矩陣（絕對值）

4.3 損傷工況

為了研究所提出的損傷識別方法是否對結構中不同位置的損傷敏感，從箱梁結構中選取具有代表性的4 個箱梁單元進行損傷識別分析，所選取的4 個箱梁單元的編號分別為3、9、22 和28，箱梁編號如圖5 所示。一共模擬6 種箱梁結構損傷工況，包含4 種單損傷工況和2種多損傷工況。各損傷工況具體配置如表1 所示。

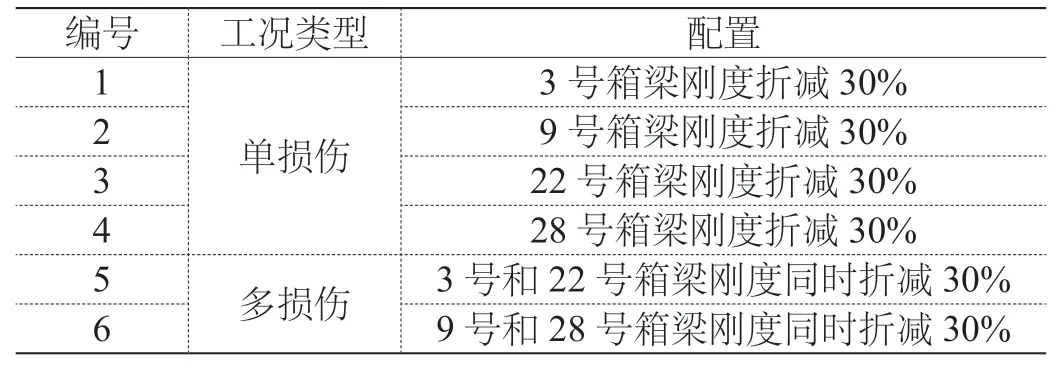
表1 箱梁結構損傷工況

4.4 損傷識別結果

利用損傷前后斜拉索索力變化和斜拉索索力對箱梁損傷的靈敏度，可以建立如公式（3）所示的求解方程。使用稀疏正則化算法對公式（3）進行求解，得到各損傷工況的剛度折減系數SRF。

箱梁結構單損傷工況的損傷識別結果如圖7 所示。從圖中可以看出，在實際損傷位置處，剛度折減系數SRF 的識別值十分明顯，而其他位置處剛度折減系數SRF 的識別值為零或者接近零。并且，3、9、22 和28號腹桿處剛度折減系數SRF 的識別值分別為-0.312、-0.307、-0.336 和-0.319，與實際值-0.3 吻合較好。以上結果表明，所提出的損傷識別方法能夠準確識別裕溪河特大橋箱梁結構中不同位置的損傷，并且識別出的損傷程度接近實際損傷程度。

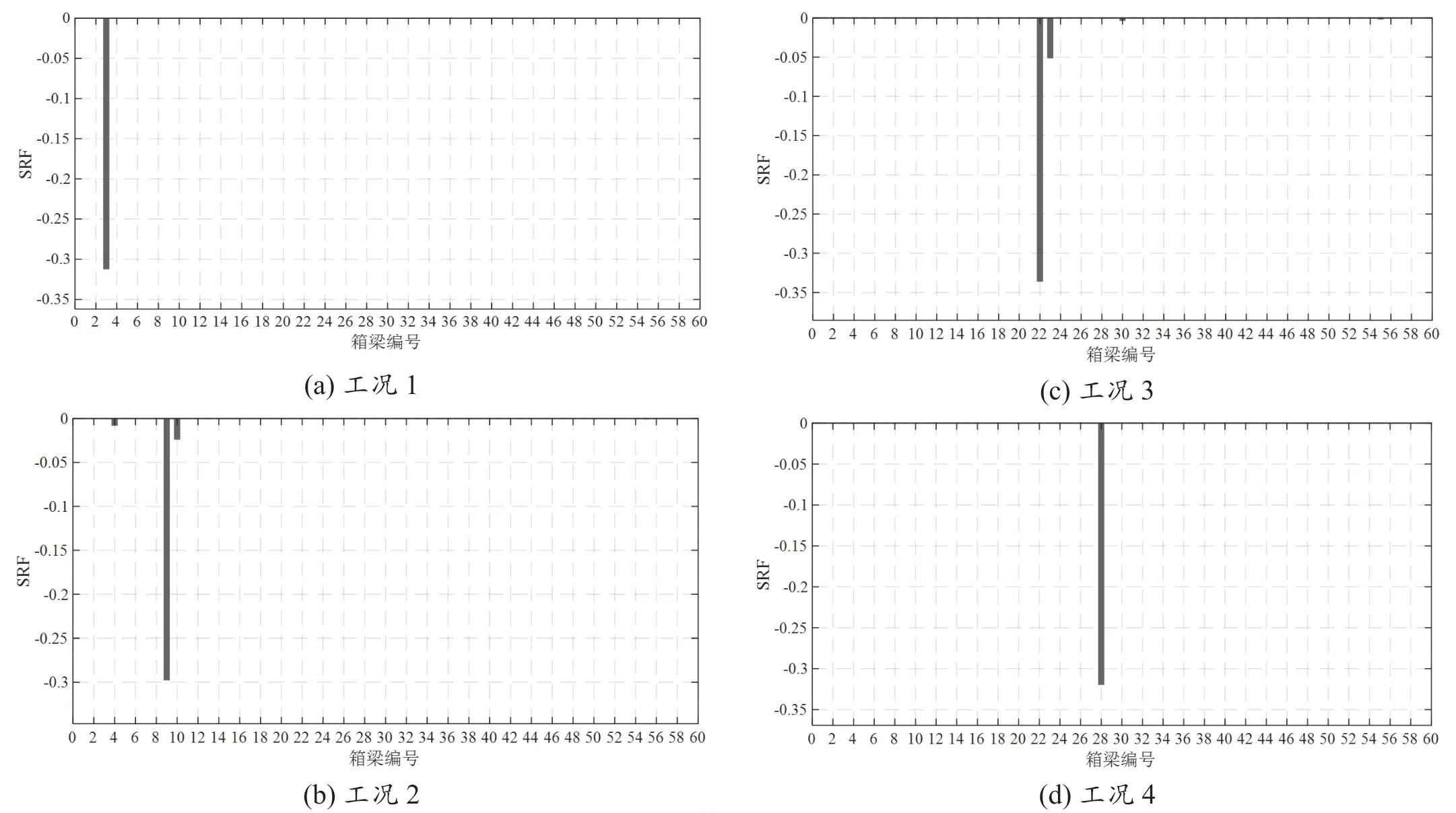
圖7 單損傷工況識別結果

箱梁結構多位置損傷的識別結果如圖8 所示。從圖中可以看出，在實際損傷位置處，剛度折減系數SRF 的識別值十分明顯，而其他位置處剛度折減系數SRF 的識別值為零或者接近零。對于工況5，3 號箱梁單元處剛度折減系數SRF 的識別值為-0.414，與實際值-0.3一致；22 號箱梁單元處剛度折減系數SRF 的識別值為-0.347，與實際值-0.3 接近。對于工況6，9 號箱梁單元處剛度折減系數SRF 的識別值為-0.336，與實際值-0.3 接近；28 號箱梁單元處剛度折減系數SRF 的識別值為-0.408，與實際值-0.3 一致。以上結果表明，所提出的損傷識別方法可以正確識別裕溪河特大橋箱梁結構中多個位置同時發生的損傷，并且識別出的損傷程度與實際損傷程度一致。

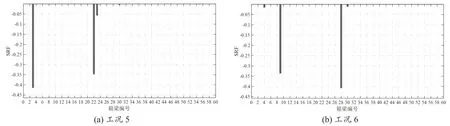
圖8 多損傷工況識別結果

5 結論

為了識別斜拉橋結構中的損傷，該文提出了一種基于索力的大跨斜拉橋結構損傷識別方法。針對裕溪河特大橋數值模型的計算結果表明，所提出的損傷識別方法可以正確識別裕溪河特大橋桁架和箱梁結構中的單位置損傷和多位置損傷，并且識別出的損傷程度與實際損傷程度一致。