面向通信抗干擾的智能反射面魯棒波束賦形設計*

辜怡然，方 貴，何松濤，秦思娜，李天晨，管新榮

（中國人民解放軍陸軍工程大學，江蘇 南京 210007）

0 引言

隨著科技水平的進步，我國的信息交流得到了顯著增強，無線通信技術的重要性也日益增加。無線通信已成為人們常用的溝通方式，并廣泛應用于人們的日常工作和生活中[1-3]。對于軍事領域來說，高效可靠的戰場無線通信是獲取戰場信息、暢通指控鏈路的重要保障，是信息化、智能化戰場條件下決定戰爭勝負的重要一環。

然而，由于無線通信的開放特性，在實際的戰場環境下，敵方可能會采取多種干擾手段對通信系統進行干擾，從而使通信無法進行或者信息完整性受到破壞。干擾信號會極大地降低合法通信的網絡質量，甚至阻斷正常的通信鏈路，導致通信癱瘓。因此，為了在戰時獲得信息層面的優勢，并提高基于信息系統的作戰能力，各個世界軍事強國紛紛將抗干擾技術作為通信技術研究的重中之重。傳統的抗干擾方法，通過跳頻、擴頻等方式，可以一定程度上解決以上干擾所帶來的問題。但隨著電子對抗裝備技術的發展，傳統抗干擾方案面對敵方寬頻譜、大功率的干擾時收效甚微，抗干擾效果受到嚴重影響。文獻[4]中提到了跳頻技術存在一些缺陷和不足，主要包括以下幾點：

（1）跳頻技術需要占用大量的頻帶寬度，這可能導致頻譜資源的浪費；

（2）跳頻技術在參與節點數較多且動態建立的通信網絡中容易引發共址干擾問題，影響通信的穩定性和可靠性；

（3）擴頻技術的應用方式存在一些靈活性不足的問題，特別是在生成和預分配擴頻參數方面，這使得擴頻系統的配置和調整相對困難，缺乏適應不同場景需求的靈活性；

（4）由于同步時間的延長或無法實現同步，擴頻技術還存在潛在的通信可靠性問題，這可能影響通信的穩定性和數據傳輸的完整性；

（5）頻繁而瞬時的跳頻操作會導致系統吞吐量的損失，這是因為在跳頻過程中，系統需要暫停數據傳輸并進行頻率切換，從而導致傳輸效率的降低；

（6）采用更高速率的跳頻將對專用集成芯片和電路提出更高的要求，因為這需要更快的信號處理能力和更高的頻率適應性，以確保跳頻過程的實時性和穩定性。

為了有效應對相應挑戰，迫切需要一種更有效的抗干擾措施。近來，智能反射面（Intelligent Reflecting Surface，IRS）被提出，并作為一項革命性的新技術用于提高未來無線網絡的性能。具體而言，智能反射面是電磁超表面的一種，由大量低成本的反射單元組成。通過有效設計反射單元的相移，智能反射面能夠實現對入射電磁波的定向反射，以智能地重新配置無線傳播環境，從而提高無線通信系統性能[5-10]。智能反射面的這一獨特性能優勢為解決戰場通信抗干擾難題提供了新思路：通過動態調整智能反射面各反射單元的反射系數，能夠有效調控敵方干擾鏈路及我方通信鏈路，從而實現對敵方信號的有效抑制和對我方信號的有效增強，從而大幅提升抗干擾效果。因此，關于智能反射面的抗干擾應用已得到初步研究。例如，文獻[6]考慮了智能反射面輔助無人機通信抗干擾的場景，運用塊坐標下降法、連續凸逼近等方法優化了無人機的飛行軌跡、智能反射面系數和地面節點的發射功率，驗證了智能反射面在無人機通信抗干擾領域的重要意義。

然而，在復雜對抗的戰場環境下，受限于對敵干擾機定位誤差等現實因素，往往難以獲取敵干擾機的準確位置及精確的干擾信道狀態信息，這給基于智能反射面的通信抗干擾方案設計帶來了新的挑戰。目前，有關智能反射面輔助的通信抗干擾魯棒設計仍然是一個懸而未決的問題，需要更多的研究與探索。為此，本文提出了一種面向通信抗干擾的智能反射面魯棒波束賦形方法。具體而言，首先建立了敵方干擾節點位置的有界誤差模型，推導了接收信干噪比表達式，并以信干噪比最大化為目標進行了優化問題建模。由于變量的耦合性及目標函數的非凸性，上述優化問題難以直接求解。為了解決以上難題，本文提出了魯棒迭代優化算法，利用半定松弛及引入松弛變量獲得了原始問題的次優解。仿真結果表明，與基準算法相比，本文提出的算法通過在地面節點附近部署智能反射面，即使在無法獲取干擾機精確位置的條件下，依然能顯著提高抗干擾性能。

1 系統模型與優化算法

1.1 系統模型

考慮如圖1 所示的通信場景，假設發送機、干擾機裝配單天線，發送機和干擾機的功率分別為Ps和Pj。發送機與接收節點之間、發送機與智能反射面之間、干擾機與接收節點之間、干擾機與智能反射面之間和智能反射面與接收節點之間的無線信道分別記為hsu，，hju，，hru。為便于表示，定義反射系數向量v=(v1,v2,…,vN)，即一個以反射系數vn為元素的向量。智能反射面配備了M個反射元件組成的均勻矩形陣列和智能調整每個元件的相移控制器，有M=Mx×Mz，其中Mx，Mz分別表示智能反射面在x軸和z軸的單元數目。設為第n個智能反射面的對角相移矩陣，其中θi∈[0,2π)，i∈{1,2,…,N}為反射元件的相移。發射機與接收節點之間除了存在直傳鏈路，還存在由智能反射面提供的反射鏈路，這一鏈路依次由發送機與智能反射面之間的信道、智能反射面反射系數向量、智能反射面與接收節點間的信道3 部分組成。由此，智能反射面提供的反射鏈路可表示為Γhru。

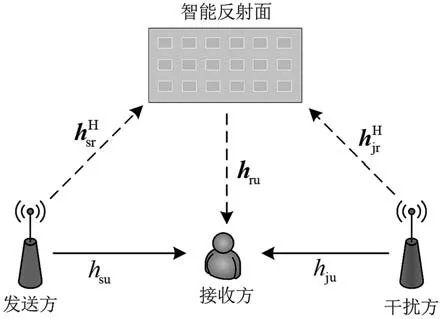
圖1 部署智能反射面的通信系統

假設發送機發送信號為x1，則目的節點接收的信號可表示為：

式中：z為噪聲，服從復高斯分布z～C(0,σs2)，σs2為接收處噪聲的功率。同理，假設干擾機發送信號為x2，則目的節點接收到的干擾可表示為：

1.2 優化算法

假設通過現有的干擾源定位技術能夠對干擾機位置進行定位。然而，由于干擾的移動性或是干擾源檢測技術的誤差，實際定位的位置信息往往存在一定的誤差。因此，本文假設對于接收機來說，發送機的位置是已知的，而干擾的位置是部分可知且存在誤差的。假設干擾的估計位置，即半球的中心位置可以獲知，為

因此，可通過式（3）對干擾機位置進行建模。

式中：(Δxj,Δyj,Δzj)∈εj為干擾估計位置和實際位置的誤差，其受以下限制：

式中：Dj為半球的半徑。從而可以得到信道增益，接收機接收信干噪比可以表示為：

式中：σ2為接收機和干擾處加性高斯白噪聲的功率；Pj為干擾的傳輸功率。

根據干擾節點位置設計有界誤差模型，干擾節點的信道增益值一定在一個范圍內，因此用Ψ1和Ψ2分別表示和hju的信道狀態信息的取值范圍，即：

式中：βju，βjr分別為衰落的幅度，min 與max 分別代表由干擾不確定度決定的幅度最小與最大界限。另外，先處理智能反射面的相位，該過程表示為：

式中：τ為一個任意的相位改變。因此，再根據aHΓb=vHdiag{aH}b的等式轉化關系，接收信干噪比可以重新表示為：

式中：ht=(diag{h0}hj)t；αt為第t個樣本的加權值。則式（11）可以展開為：

不等式取等號的條件為：

還有加權值的約束條件：

結合上述公式，可以求得加權系數的解為：

1.3 IRS 相移矩陣優化

由于目標函數相對復雜而且多個變量耦合在一起，較難直接得到接收功率R的最大值。筆者注意到，log(·)函數是一個單調遞增的函數，要實現系統平均速率最大化的目標，等價于通過找到一組相位矩陣，使得目標函數的信干噪比最大。此時，問題可以等價表示為：

式中：Vl,l為V的第(l,l)個元素的值。然而，秩為1的約束是非凸約束，使用半定松弛方法，先忽略秩為1 的限制求解，再通過高斯隨機化或者特征值分解的方法獲得可行解。引入中間變量k，并定義=kV，由此，公式（19）可轉化為：

上述問題是一個標準的凸優化問題[11]，可以通過凸優化求解工具有效解決。然而，秩為1 的限制條件此時不能保證達到。具體地，若V的秩為1，則可以通過特征值分解直接求得v；否則，要通過高斯隨機化近似求得v。具體細節參考文獻[5]。因此，智能反射面相位系數為：

2 仿真實驗

對于上文所提算法，本節通過仿真實驗驗證有效性。“干擾位置精確/非精確”表示干擾位置是已知與部分已知的情況。“無IRS”表示沒有部署智能反射面，本文的仿真參數為：發送信號的功率為10 W，干擾最大功率為100 W，參考距離下的信道增益為ρ=-3 dB，智能反射面的單元個數為N=40，高斯白噪聲功率為σ2=-80 dBm。

圖2 展示了接收節點的信干噪比隨智能反射面反射單元數目的關系。從圖中可以看出，部署智能反射面可以提升信干噪比，且隨著智能反射面單元數目的提升，信干噪比有持續的提升。因為智能反射面單元數目的增加可以增加從智能反射面反射的鏈路數量，所以接收節點可以接收到更多從智能反射面反射的增益信號，使得信干噪比持續提升。

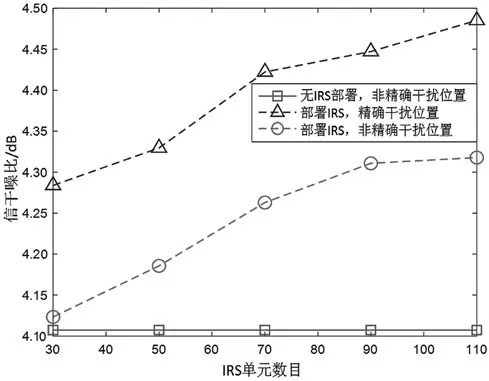
圖2 信干噪比與IRS 單元數目的關系

圖3 展示了信干噪比與干擾功率的關系。從圖中可以觀察得到，隨著干擾功率的提升，信干噪比有所下降。而在同一干擾功率下，部署智能反射面后，信干噪比明顯提高，說明用智能反射面來輔助通信抗干擾效果明顯。此外，相比干擾位置非精確的情況，觀察到干擾位置精確的情況下，系統信干噪比更大，在部署智能反射面后，其信干噪比下降幅度也不大，說明本文所提的魯棒算法實現了對智能反射面波束賦形的魯棒設計，干擾位置非精確同樣能夠高效提升系統信干噪比。

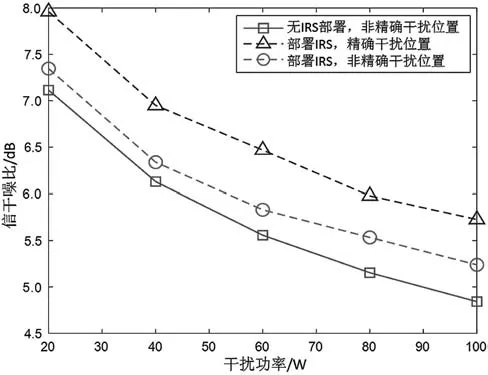
圖3 信干噪比與干擾功率的關系

3 結語

針對戰場環境下難以獲取干擾節點精確位置信息的問題，本文通過對干擾位置進行凸包建模，將非凸的信干噪比最大化問題進行轉凸迭代求解。仿真結果表明，本文所提的算法實現了智能反射面輔助通信抗干擾波束賦形的魯棒優化，相比于無智能反射面的情況，系統信干噪比得到了顯著提升。下一步研究將會考慮在敵方干擾節點信息完全未知情況下的智能反射面波束賦形優化問題。