基于雙圖轉換和融合CRNN網絡的軸承故障診斷

李 喆, 吐松江·卡日, 范 想, 范志鵬, 萬容齊, 白新悅, 吳俁潼

(新疆大學 電氣工程學院,烏魯木齊 830046)

滾動軸承廣泛用于各種旋轉機械,在支撐旋轉的同時常常受到沖擊載荷與交變載荷等作用,成為運行環境最惡劣、承擔負擔最重的零件,極易產生損傷進而影響整個設備的運行[1];據統計,軸承故障率占到所有旋轉機械故障的40%～55%[2]。因此,如何準確地進行滾動軸承故障診斷成為各相關領域面臨的重要問題。

振動信號分析是一種最常見的滾動軸承故障診斷方法,其無需拆卸機器部件即可挖掘和分析故障類別[3]。該方法主要可分為特征提取與類型識別兩步:首先通過時頻域方法,如經驗模態分解(empirical mode decomposition, EMD)[4]、小波變換(wavelet transforme, WT)[5]、變分模態分解(variational mode decomposition, VMD)[6]等,從原始信號中提取能反映軸承故障點的特征,并構建特征向量;隨后利用人工智能診斷技術,如支持向量機[7]、隨機森林[8]、多層感知機[9]等,對特征向量進行故障類型識別。雖然傳統的人工智能算法已經在軸承故障診斷領域取得了一定效果,但是其對復雜非線性問題學習能力不足,不適用于處理大容量樣本,并且較為依賴信號處理技術和人工經驗。

近年來,深度學習作為新興的數據分析方法被廣泛應用于旋轉機械故障診斷。其中,卷積神經網絡(convolutional neural network,CNN)使用最為廣泛,并取得了理想效果。基于CNN的故障診斷方法種類繁多,可按輸入維度分為兩類,第一類方法使用一維振動信號作為CNN的輸入。例如,曲建嶺等[10]提出了基于端到端的自適應一維卷積神經網絡(ACNN-FD)故障診斷算法,通過“時間步”對原始一維數據進行劃分后作為輸入。李恒等[11]對滾動軸承振動信號進行短時傅里葉變換,得到時頻譜樣本輸入卷積神經網絡。然而,原始信號不能顯著地表示故障特征,并且大多數已知的CNN模型更容易從高維數據中提取特征信息。因此,通過圖像識別模型提高時序分類的精度成為滾動軸承故障診斷領域的研究熱點之一。第二類方法將一維信號轉換為二維圖像,然后利用二維卷積神經網絡實現故障診斷。例如,袁建虎等[12]將振動信號進行連續小波變換(continue wavelet transform, CWT)后,再將所得時頻圖輸入CNN分類器模型。Wen等[13]提出了一種將一維振動信號轉換為二維灰度圖像后作為CNN輸入的方法,取得了較好的診斷效果。但上述方法中,時頻圖無法反映原始信號的完整信息且易受到人工經驗的影響,而灰度圖像按行堆棧像素而成,難以反映信號中包含的時間信息。為克服上述缺點,格拉姆角差場(Gramian angular difference field,GADF)變換、馬爾可夫轉移場(Markov transition field,MTF)變換等圖像轉換方法,在對數據重構時,避免了一維信號信息的丟失,并保留了與時間的相關性。仝鈺等[14]提出通過使用GADF變換可以將一維信號轉換為二維圖像,并研究發現GADF圖像比灰度圖像、時頻圖像更容易被CNN識別。雷春麗等[15]采用MTF編碼方式將原始一維振動信號轉化為二維特征圖像,然后通過CNN進行自適應特征提取和故障診斷。近年來,以卷積循環神經網絡(convolutional recurrent neural network,CRNN)為代表的深度學習技術在自然語言處理和計算機視覺上展現了突出的能力,該方法本質上就是利用多像素表征樣本差異性,從而更好地獲取時間序列的深層特征,因此CRNN模型也被應用到軸承故障診斷領域。張訓杰等[16]利用GADF將滾動軸承一維振動信號轉換為二維圖像數據,并提出基于CNN與雙向門控循環單元(bidirectional gated recurrent unit,BiGRU)的CRNN診斷模型。

盡管GADF或MTF方法生成的圖像保留了振動序列的空間和時間依賴性,在CRNN上實現了故障診斷的功能,但是單一的二維映射存在一定的局限性,且沒有充分挖掘CRNN對高維特征提取能力。因此,本文從數據輸入形式和特征提取方法兩方面著手,針對滾動軸承原始故障數據,提出一種基于雙模態圖轉換和融合CRNN網絡的電機軸承故障診斷方法,具體過程如下:

(1) 分別用格拉姆角差場和馬爾可夫轉移場實現原始一維序列數據的圖轉換,并用轉換后的兩種圖像共同構成模型輸入。

(2) 提出并構建了一種融合循環卷積神經網絡,名為Fu-CRNN,該網絡分別提取兩種圖像的相關特征后,將特征融合以進一步提高網絡特征表達能力。

(3) 通過分類器實現對不同故障類型的分類。

本文選用來自凱斯西儲大學軸承故障試驗平臺的數據驗證所提方法的優越性,通過將不同負載數據分布到訓練集、測試集和驗證集來評估所提方法的有效性及泛化能力,并分別與GADF圖像、MAR圖像作為輸入的CRNN網絡以及其他常見網絡進行對比分析。實際算例測試結果表明,該方法在軸承故障診斷問題上相較于傳統模型具有更優的性能。

1 基本理論

1.1 格拉姆角差場

GADF是一種圖像編碼方法,在極坐標系上表示時間序列后,通過GADF矩陣對一維振動信號進行編碼來生成包含時間特征的二維圖像[17]。假設時間序列X如式(1)所示

X=[x(1),x(2),x(3)…,x(n)]T

(1)

GADF的轉換過程可以分為兩部分。

第一步:將X中的x(i)通過使用如下歸一化操作縮放到區間[-1,1],表達式如式(2)所示

(i=1,2…n)

(2)

(3)

式中:φi為極坐標余弦角;ti為時間戳;r為由時間戳映射的半徑;N為生成空間中對極坐標系進行正則化的常數因子。對于取值區間為[-1,1]的時間序列,余弦角在極坐標系上單調分布于[0,π]之間,因此時間序列X在極坐標空間中具有唯一逆映射。

第二步:對于存儲時間信息并計算各極坐標三角差的參數φ,該系統可編碼為GADF矩陣,表達式如式(4)所示

(4)

式中,I=[1,1,…,1]是單位行向量。矩陣的運算形式對應于正則內積的懲罰形式。此外,矩陣的正對角線中,時間趨勢從左上角到右下角表示,因此時間序列的時間相關性得到了很好的保留。

1.2 馬爾可夫轉移場

馬爾可夫轉移場是一種將時序信號編碼為二維矩陣的方法,該方法能表示時間和概率的動態變化[18-19]。假設一個時間序列為X=[x(1),x(2),…,x(n)]T,其數值可以離散化到Q個分位數單元(bin)中,每個x(i)可以分配給一個相關的分位數qj(j∈[1,Q]),通過沿時間軸以一階馬爾可夫鏈的方式計算bin之間的遷移概率,得到Q×Q大小的馬爾可夫遷移矩陣W,表達式如式(5)所示

(5)

式中,wij=P(x(t)∈qi|x(t-1)∈qj),wij為qj中元素x(t-1)伴隨qi中元素x(t)的概率,即分位數qi位于分位數qj后的概率,又稱為一步轉移概率。

由于矩陣W忽略了X分布與時間步長t(i)間的時間對應關系,故構造MTF來彌補時間信息損失。MTF通過沿時間順序重新排列k(k=1,2,…,n)步轉移概率,得到包含時間步長與每個bin相關性的矩陣M,其表達式如式(6)所示

(6)

式中:Mij為時間序列信號xi映射的bins轉移到xj對應的bin的概率。在MTF矩陣中,Mij可以看作是像素點,因此可以通過MTF將時間序列轉換為圖片表示。

1.3 CRNN網絡

CRNN是一類包含卷積計算且具有深度結構的前饋神經網絡,主要用于端到端地識別圖像文本,將圖像識別轉化為時序依賴的序列學習問題[20]。典型CRNN網絡由CNN與BiGRU級聯形成,其結構如圖1所示。

圖1 CRNN網絡結構圖Fig.1 The structure of CRNN network

CRNN既具備CNN提取局部特征的優勢,又擁有BiGRU提取序列全局特征的長處,其中CNN是由二維卷積和最大池化層組成,即標準CNN中去除全連接層。CNN模塊的作用是從輸入圖像中提取特征序列X,X=(x1,x2,…,xT),其中特征向量xt對應第t個特征映射,更進一步說,xt是由所有特征映射的第t列生成的特征向量連接而成,每一列的寬度被設置為一個像素。因為卷積層、最大池化層和激活函數的平移不變性,所以每一列的特征映射對應著原圖中的一個矩形區域,即感受野。感受野與其在特征圖中相對應的列順序相同,因此特征序列中的特征向量與原圖中的感受野一一對應,如圖2所示。

圖2 感受野映射說明Fig.2 Illustration of the map of receptive fields

在二維卷積及池化層后級聯的BiGRU由兩層相反傳播方向的門控循環單元(gated recurrent unit,GRU)組成。GRU被認為是循環神經網絡的(recurrent neural network,RNN)的加強版,在繼承了短期記憶能力的同時,還避免了RNN在訓練過程中出現的梯度消失問題。與另一種常見的RNN變體長短期記憶網絡(long short-term memory,LSTM)相比,GRU不僅和LSTM一樣解決了梯度消失問題,而且還精簡了框架結構,減少了四分之一的參數,進而提升了模型訓練速度。

BiGRU相較于GRU對時間特征序列有更強的上下文信息提取能力,可捕捉到GRU無法表征的特征。BiGRU包含的兩個GRU分別按照順序和逆序傳播,每個GRU提取某一節點時間序列與其前后片段的關系,將在CNN層生成的特征序列X中的每一個向量xt預測為一個分布概率,然后通過全連接層映射到樣本標記空間,此時特征數量與分類數量一致,最后經過分類層及概率歸一化后得出預測值。

2 基于Fu-CRNN網絡的診斷模型

GADF和MAR方法分別從極坐標和馬爾科夫轉移概率的角度對一維信號進行編碼,擁有深層次相關性特征表征能力。為了結合它們的優點,本文基于由原始一維時間序列數據轉換而成的兩種模態的二維圖像數據,提出Fu-CRNN網絡診斷模型。該模型在數據重構模塊完成振動信號的二維化后,將生成的兩種圖片依次輸入到特征提取模塊,經特征融合模塊運算后,輸出預測結果并完成故障診斷。模型結構如圖3所示。

圖3 基于Fu-CRNN網絡診斷模型Fig.3 Diagnosis model based on Fu-CRNN network

2.1 特征提取模塊

特征提取模塊是典型的CRNN網絡,由CNN模塊和BiGRU模塊級聯組成,其中CNN模塊由7層固定大小的3×3卷積層和5層最大池化層組成,主要用來學習樣本圖像的紋理、角度和邊緣等特征。為了獲取更深層次特征,采用激活函數對特征映射進行非線性處理。在激活函數后添加最大池化層,池化層除了實現下采樣、降維和非線性等功能,還調整特征映射的尺寸使得最終特征映射為向量形式。隨后在CNN模塊后級聯BiGRU模塊,BiGRU將在CNN生成的特征序列S=(S1,S2,…,ST)中的任意向量St預測為標簽概率分步yt,其中t∈[1,T],St為高和寬都為一個像素的感受野。GADF圖像(G)和MTF圖像(M)生成的yt組成新的特征序列G′和M′,進入下一層網絡。

2.2 特征融合模塊

特征提取模塊分別從GADF和MTF圖像數據中提取得到不同的特征序列后,為了能讓模型同時學習到上述兩類特征,對兩種模態圖像經過同一模塊處理后的不同模態輸出進行拼接(Concat),從而生成新的融合特征向量。拼接定義如式(7)、(8)所示

Mcat=fcat(M1,…,Ml)=[M1,…,Ml]

(7)

其中,

(8)

拼接函數將CRNN模塊提取到的兩類圖像的特征信息整合后,新向量被輸入到神經元數量為100的全連接層,并通過激活函數進行非線性特征學習,最后由Softmax函數判定故障類型概率,概率值最大的即為預測結果。盡管Fu-CRNN網絡包含若干種網絡構架,但是仍可以在一個損失函數下進行訓練,是一種端到端的網絡,其整體構架如表1所示。

表1 模型結構示意圖Tab.1 Illustration of model structure

3 算例分析及對比試驗

3.1 試驗數據

算例數據采用來自于凱斯西儲大學(CWRU)的軸承故障數據集[21]。所用數據由置于電機驅動端加速度傳感器所采集的振動信號構成,采樣頻率為12 kHz,采集時長10 s,包含4個正常信號、77個外圈損傷信號、40個內圈損傷信號及40個滾動體損傷信號,每條信號含有約121,000個數據。數據集分為10類,包含9種不同故障類型(3種故障部位:外圈、內圈、滾珠,每個部位有3種故障尺寸:0.18 mm、0.36 mm、0.54 mm)以及1種正常類型。

將每段信號按固定滑窗尺寸隨機截取,每類故障信號被劃分為4 000個樣本。為驗證模型在不同負載與轉速情況下的泛化能力,將不同負載與轉速的樣本按照8:1:1的比例劃分為訓練集、測試集和驗證集,其中A數據集和D數據集作為訓練集,B數據集為測試集,C數據集為驗證集,樣本構造如表2所示。

表2 滾動軸承樣本構造Tab.2 Sample structure of rolling bearing

3.2 圖像轉換

在本試驗中,軸承最低轉速為1 730 r/min,由公式N=60f/n計算出每圈所采集的數據量為416。為保障每個樣本包含完整的周期信息,并使圖像尺寸易于管理,有必要分析不同尺寸滑窗裁剪后的數據長度對Fu-CRNN網絡效果的影響。此外,MTF圖像編碼方法中的參數——分位數(n_bins)也影響模型的最終性能,因此采用3.1節中數據進行試驗,其中網絡參數仍如表1所示。經驗證,數據長度為1 000,n_bins為10時,模型能充分學習時間相關性,取得最高的預測準確率,如圖4所示。

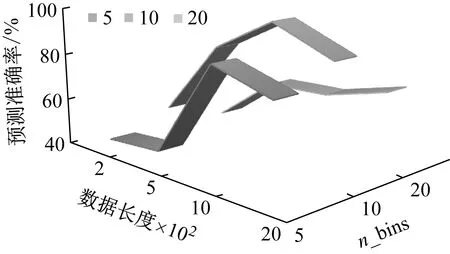
圖4 數據長度和n_bins對模型預測精度影響Fig.4 Impact of data length and n_bins on accuracy

若按照MTF原理直接將截取的樣本序列轉化為1 000×1 000像素的MTF圖像,則存在諸多弊端,除了圖像尺寸過大導致算力需求過高外,更重要的是采樣頻率過高會使相鄰點變化率趨近于零。為了提高計算效率并突出MTF圖像表征性能,采用模糊核(blur kernel)不重疊的對每個m×m像素區域進行平均,其中m為圖像的邊長。GADF編碼方法同樣面臨圖像龐大導致算力浪費的問題,因此采用與MTF圖像相同的處理辦法。

樣本通過格拉姆角場和馬爾可夫變遷場分別轉換為對應圖像后,再經過壓縮,最終生成的圖像分辨率均為200×200。由上述兩種轉換方法生成的不同故障狀態下的圖像分別如圖5和圖6所示。

(a) 滾動體故障0.18 mm

(d) 滾動體故障0.36 mm

(e) 內圈故障0.36 mm

(g) 滾動體故障0.54 mm

(h) 內圈故障0.54 mm

(i) 外圈故障0.54 mm

(j) 正常狀態圖5 GADF編碼軸承故障圖Fig.5 GADF code bearing fault map

(a) 外圈故障0.18 mm

(b) 內圈故障0.18 mm

(c) 滾動體故障0.18 mm

(e) 內圈故障0.36 mm

(f) 滾動體故障0.36 mm

(g) 外圈故障0.54 mm

(h) 內圈故障0.54 mm

(i) 滾動體故障0.54 mm

(j) 正常狀態圖6 MTF編碼軸承故障圖Fig.6 MTF code bearing fault map

3.3 網絡訓練

試驗模型基于Python的Pytorch框架搭建,所用硬件配置為CPU i7-9750H、GPU GTX-3060、8GB內存。根據超參數對最終模型性能的影響,選取batch_size為64,參數優化器為SGD隨機梯度下降優化器,并且采用給定間隔調整學習率策略。初始化模型參數后,使用訓練集A、D對模型進行訓練,用驗證集C對每輪訓練后的模型測試準確率和損失值,訓練完成后用測試集B評估模型性能。

圖7為基于Fu-CRNN網絡模型迭代300輪后所獲得的準確率、損失值折線圖。從圖中可以看出,訓練模型在迭代了43次時,訓練集的準確率達到99.93%,測試集準確率達到99.86%,損失均降低至0.001,模型達到完全收斂,此后訓練集與測試集的準確率和損失值趨于水平方向穩定,由此證明本文所提出的基于雙圖轉換和Fu-CRNN網絡的模型在對滾動軸承進行故障診斷時是可行、有效的。

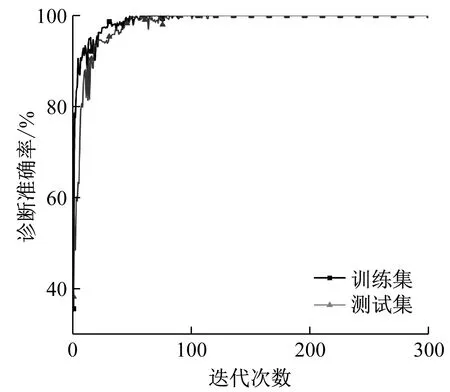
(a) 準確率

(b) 損失曲線圖7 Fu-CRNN網絡診斷曲線圖Fig.7 Fu-CRNN model diagnosis curve

為了進一步分析Fu-CRNN對GADF和MTF編碼圖的特征學習與故障分類能力,繪制了如圖8所示的滾動軸承分類混淆矩陣。由圖8可知,坐標值0～9分別表示滾動軸承的10種狀態,對角線上的深色區域為每類故障歸一化后所對應的準確率,其余部分的數值為誤分類率。例如實際類別3與預測類別9對應位置的數值為0.001,即在測試集有1個類別3的故障被誤分類為類別9,具體含義為有1個0.36 mm外圈故障被錯誤的分類為正常狀態,此外還有1個類別為4的故障被誤分類為類別9,即有1個0.36 mm外圈故障錯誤分類為正常狀態。綜合圖8所有數據可知,在第0、1、5、6、7、8類的滾動軸承故障分類中均取得了很高的診斷效果,而在第2、3、4、9類故障分類中也取得較高的準確率。可以說明,雙圖轉換和Fu-CRNN網絡相結合的方法可以在該診斷試驗中取得較為滿意的分類效果。

圖8 滾動軸承分類混淆矩陣Fig.8 Rolling bearing classification confusion matrix

3.4 不同模態圖像數據對比分析

為驗證本文所提方法的優越性,分別用CWT、GADF和MTF轉換方法生成的二維矩陣單獨作為CNN-BiGRU 即CRNN網絡的輸入。同時為突出GADF和MTF圖像轉換方法的優勢,對一維振動信號轉換后的CWT、GADF和MTF圖像兩兩組合輸入到Fu-CRNN模型。根據單一變量原則,CWT樣本、GADF樣本和MTF樣本直接采用之前生成的樣本,數量均為100 000條,且劃分方法也與前文一致。當迭代次數取300時,各模型訓練得到的測試結果如圖9所示。

圖9 Fu-CRNN模型診斷曲線圖Fig.9 Fu-CRNN model diagnosis curve

從圖9中可以看出,CRNN模型在測試集上對于CWT、GADF和MTF轉換圖像的識別準確率分別為88.51%、94.72%和90.79%,均低于本文所提診斷方法取得的準確率(99.86%),這表明兩種圖像經Fu-CRNN網絡融合后包含更豐富的特征知識,對于模型的分類識別具有更優越的效果。在基于雙模態組合模型中,GADF+MTF在故障識別上準確率最高(99.86%),而GADF+CWT和MTF+CWT的準確率分別為97.74%和92.67%,充分表明了GADF和MTF相較于以CWT為代表的時頻圖像時,可以更完整地保留原始信息,從而保障更高的準確率。

3.5 與其他算法對比分析

為了更近一步驗證本文所提模型的有效性,將本文方法中的特征提取模塊分別替換為CNN-GRU、ResNet以及LeNet5進行對比分析,同時對每種網絡在不同模態圖像作為輸入時的表現分析對比。

每個模型均使用前文中的圖像樣本集進行試驗,試驗的最終結果如表3所示。從表3可以看出任一網絡在雙圖輸入時的識別準確率高于單一圖像輸入時,充分體現出特征融合模塊對于識別效果的提升。而在雙圖輸入網絡中,CNN-BiGRU的故障診斷精度比CNN-GRU、ResNet以及LeNet5均有所提高,這表明CNN-BiGRU作為特征提取模塊時對空間與時間相關性的提取更加充分。盡管目前基于CWRU數據集開展的研究成果中,已有使用GADF方法的端對端網絡[22-23]或采用MTF轉換圖像作為輸入,其訓練集識別率均達到100%,均高于本文所建模型的訓練集識別率0.07%,但針對測試集的故障識別率,上述模型識別率分別為99.08%、99.67%和99.35%,本文所建模型識別率(99.86%)分別高于上述模型0.78%、0.19和0.51%,具有最高診斷精度。盡管由于不同故障識別模型的學習策略、樣本劃分、基礎分類器的差異導致訓練集識別率存在區別,但是本文所建模型在測試集上具有最優識別性能。總的來說,本文所建模型相較于傳統診斷模型能更準確、更可靠的識別軸承故障類型。

表3 不同圖像算法滾動軸承故障診斷試驗結果Tab.3 Test results of rolling bearing fault diagnosis with different image algorithms

4 結 論

為了充分發揮卷積循環神經網絡對格拉姆角差場和馬爾可夫變遷場圖像的特征發掘,本文提出了一種基于雙模態圖像轉換和融合循環神經網絡的滾動軸承故障診斷方法。利用CRNN對于圖像強大的局部特征和全局特征提取能力,分別提取由GADF和MTF方法生成圖像的特征,再將提取到的特征向量進行融合,最終由分類器實現狀態識別。試驗證明,本文所使用的方法對于滾動軸承不同故障程度以及不同故障位置的振動信號識別都取得了較好的識別效果,平均測試準確率達到99.86%,優于常見的診斷模型;且所有試驗的訓練集、驗證集和測試集均由不同載荷和轉速的數據集構成,充分驗證了模型的泛化性能。綜合上述結果,本文所提出的方法充分汲取兩種轉換方法優點并提高單一CRNN模型特征表達能力,對于滾動軸承故障模式識別有一定的實用價值,為智能故障診斷提供了具有可行的方案。在未來的工作中,針對雙模態融合方法導致診斷模型復雜度提高、時間成本增加的問題,有必要通過精簡特征提取模塊、改進訓練策略、采用輕量分類模型等方面改善,進一步發掘Fu-CRNN模型潛力。