基于LMI的分段線性系統共存吸引子轉遷控制研究

李得洋, 吳少培, 李國芳, 丁旺才, 丁 杰, 俞力洋, 衛曉娟

(1.蘭州交通大學 材料科學與工程學院,蘭州 730070; 2.蘭州交通大學 機電工程學院,蘭州 730070;3.上海應用技術大學 軌道交通學院,上海 201418)

分段線性系統是一類很有代表性的非光滑系統,它廣泛存在于實際機械系統[1-3]中,因此對此類系統的研究具有重要的理論意義和實用價值。由于此類系統具有非連續性或非光滑性,學者們主要通過解析、數值和近似解析的方法對系統周期運動的存在性、穩定性及混沌運動的生成及演化機理開展相應的研究。Shaw等[4]針對一類單自由度分段線性碰撞振動系統,通過建立系統的Poincaré映射,研究了系統周期響應的穩定性問題。Hu等[5]針對分段光滑系統,研究了非光滑向量場對系統Poincaré映射可微性的影響。利用數值和實驗方法,Ma等[6]系統研究了四類彈性碰振系統在擦邊點附近Poincaré映射的Jocobi矩陣特征值和跡的變化情況。Jiang等[7]把不連續幾何方法從含剛性約束的碰撞振子應用到含彈性約束的碰撞振子中,研究了含單邊彈性約束系統的擦邊分岔。Miao等[8]應用中心流形定理,研究了一類考慮搖頭阻尼非光滑的兩自由度輪對的Hopf分岔類型及穩定性。Floquet理論是開展分段線性系統穩定性及分岔研究的理論基礎,Leine等[9]給出了一般意義下分段線性系統周期解的Floquet理論,王強等[10]利用Floquet理論揭示了軸承外圈故障系統(等效為三自由度分段光滑系統)經Neimark-Sacker分岔通向混沌的路徑。分段線性系統往往是一個多參數系統,在多個參數協同變化下,朱喜鋒等[11]研究了一類兩自由度含間隙約束碰撞系統周期運動的參數分布區域,并揭示了系統的顫碰運動特性。Li等[12]以含兩種非光滑因素的碰撞振子為研究對象,研究了在參數平面上由擦邊分岔等引起的黏滯運動、顫振運動和周期陷窩的形成機理;并進一步分析了高頻區內系統共存吸引子及其吸引域的分布情況。

吸引子共存是非光滑系統的一種內在的特性,是指在給定參數下系統存在兩種及兩種以上的獨立動態響應。鑒于分段線性系統對初始條件的依賴性,采用胞映射法可以更全面地探索此類非光滑系統在振動中的深層次問題。林何等[13]建立了功率分流直齒輪系統非線性振動模型,結合胞映射與區域分解思想構建了全局解域求解算法,揭示了系統的全局解域特性及各種潛在動力學行為。吳鑫等[14]針對一類受擬周期激勵的具有懸臂結構的碰撞振動系統,研究了在參數變化下系統的奇異非混沌動力學及多穩態共存現象。Yue等[15]通過復合胞坐標系法,研究了一類含單邊彈性約束碰振系統的吸引子、吸引域和混沌鞍等全局性態,揭示了內部激變和邊界激變這兩類激變的演化過程。張惠等[16]利用簡單胞映射法,分析了含間隙及預緊彈簧激振系統由鞍結分岔、周期倍化分岔及邊界碰撞分岔誘導出現的吸引子共存情況。Shen等[17]研究了一類非光滑系統(雙頻驅動的鉸接式系泊塔模型)在初始條件變化時奇異的非混沌吸引子共存特征。

對于運動的主動控制而言,吸引子共存表明可通過初值擾動或施加外力實現具有不同動態特性的吸引子相互遷移。針對非光滑系統的共存吸引子轉遷研究,學者們主要針對單自由度分段線性系統[18],文獻[19]雖然利用線性反饋實現了一類兩自由度含彈性約束非光滑系統共存吸引子的轉遷,但對多態共存區的辨識及轉遷機理未作定性分析,且對控制方法的穩定性及控制參數的選取未給出解決方案。本文以一類兩自由度含間隙分段線性系統為研究對象,利用胞映射法和響應微擾計算方法對共存吸引子的分布及轉遷開展研究;同時利用系統分段線性的特性,通過構造一組線性矩陣不等式來得到線性反饋控制器實現系統共存吸引子轉遷的穩定性條件,仿真結果驗證了本文方法的可行性和有效性。通過吸引子轉遷控制可實現系統的減振、混沌控制和分岔控制。

1 系統的力學模型及運動微分方程

圖1為兩自由度含間隙分段線性系統的力學模型,質量為M1和M2的振子分別由剛度為K1和K2的線性彈簧以及阻尼系數為C1和C2的線性阻尼器連接,在簡諧激振力Fisin(ΩT+τ)(i=1,2)(其中Ω、T和τ分別為激勵頻率、時間和相位角)的作用下沿水平方向振動。以系統的靜平衡位置為空間坐標的原點建立坐標系,振子M1和M2的位移分別為X1和X2,在振子M1的右側固定有剛度為K3的彈性約束。在簡諧激勵的作用下,當振子M1的位移小于D1時,系統為兩自由度的線性振動系統;而當振子M1的位移大于D1時,振子會與右側的彈性約束發生碰撞并接觸在一起振動,由于間隙的存在和碰撞的產生,系統會表現出強非線性和非光滑的特性。

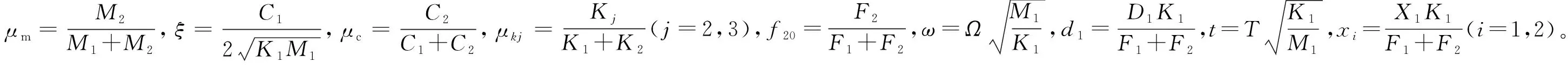
無量綱化有

(1)

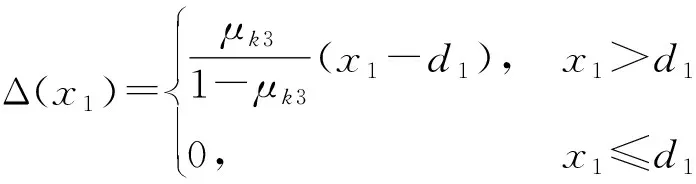
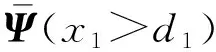
Ajsin(ωt+τ0)+Bjcos(ωt+τ0))(x1≤d1)

(2)

(3)

2 系統n-1周期運動的周期解

在系統穩定運動狀態下,取振子M1與右側約束面碰后瞬間為時間坐標原點(t=0),振子M1經歷時間t1與右側約束面脫離,再經歷時間t2與右側約束面再次碰撞,若t1和t2滿足t1+t2=2nπ/ω,系統就存在n-1周期運動(用符號n-p表示系統的周期運動,其中n為激勵周期,p表示振子以正向速度與右側約束面碰撞的次數)。系統n-1周期運動的周期條件、邊界條件和銜接條件可表示為

為便于周期運動推導,引入下列符號

n11=n22=cosωt1,n12=-sinωt1,n21=sinωt1

則系統n-1周期運動的周期解可表示為

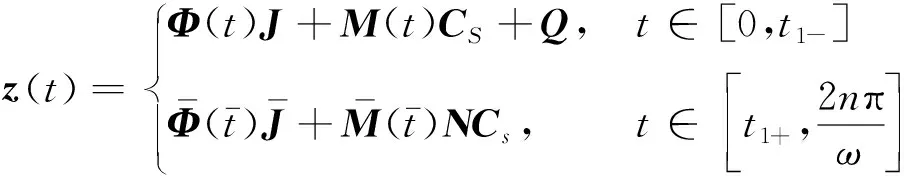
(4)

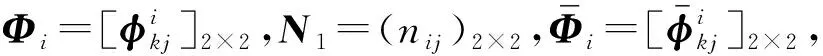
CS=[cosτ,sinτ,cosτ,sinτ]T,

Q=[ψ11c1+ψ12c2,0,0,0]T,

將t=0及t=t1+代入式(4),可得積分常數關于初始條件的表達式

J=Φ1(0)-1(z(0)-M1(0)CS-Q)

(5)

(6)

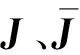
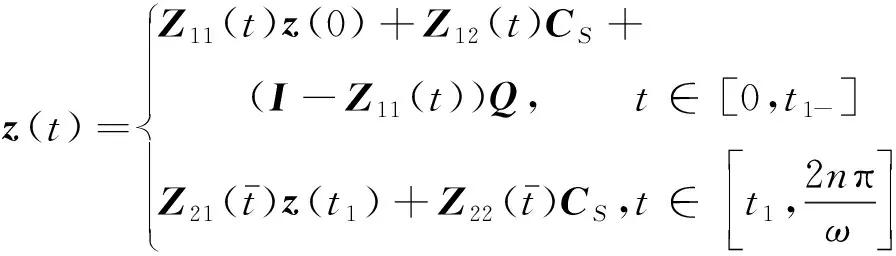
(7)

其中

Z11(t)=Φ(t)Φ(0)-1,

Z12(t)=M(t)-Φ(t)Φ(0)-1M(0),

(8)

其中

L=(Ι-Z21(t2)Z11(t1))-1(Z22(t2)+

Z21(t2)Z12(t1))=(lij)4×4;

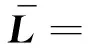
H=(Ι-Z21(t2)Z11(t1))-1Z21(t2)(Ι-

Z11(t1))Q=(hij)4×1;

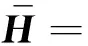
由初始條件x1(0)=d1,x1(t1)=d1可得初相位

τ=

(9)

τ=

(10)

其中

δ1=l11+l13,δ2=l12+l14,

根據初相位的表達式可得系統n-1周期運動的存在條件為

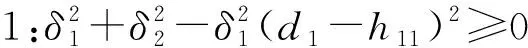
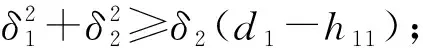
根據t1+t2=2nπ/ω,以及系統n-1周期運動的銜接條件,可得僅關于時間t1的表達式

(11)

通過數值方法可求解出方程的根t1,進而可確定系統n-1周期解。

3 系統Poincaré映射的建立及穩定性分析

為研究系統周期運動的穩定性和局部分岔問題,建立兩個Poincaré映射

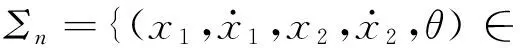
θ=mod(ωt,2π/ω)};

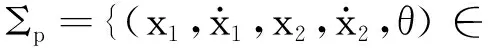
選擇定相位面Σn可以統計出系統周期運動的周期數;選擇約束面Σp可以統計出振子與約束面的碰撞次數。以定相位面Σn構造系統Poincaré映射,根據響應微擾計算方法[20]可得到系統的Floquet矩陣,具體計算步驟如下:

步驟1對系統進行求解,并確定其運動時間為nT(T為系統周期,n≥1)。

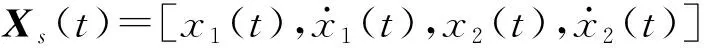
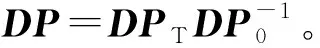
根據Li等方法可計算出系統的Lyapunov指數。Lyapunov指數既可確定周期和混沌運動的分布區域,又可甄別周期與混沌運動、周期與擬周期運動共存的區域,另外結合分岔圖和Lyapunov指數圖可研究各個共存周期運動在參數變化時出現的各種分岔。

4 基于LMI的線性反饋控制器穩定性分析

如圖1所示系統施加線性反饋控制器后,被控系統可表示為

G(x1)=fsin(ωt+τ)

(12)

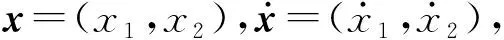
選取線性反饋增益矩陣

式中,u1、r和u2為控制參數。

將式(1)用一階形式表示

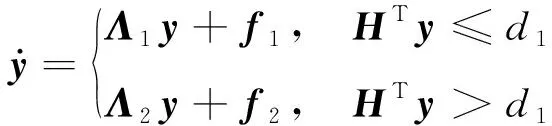
(13)

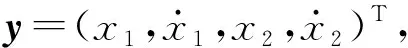
Λ2=

施加線性反饋控制器后,被控系統式(12)可表示為

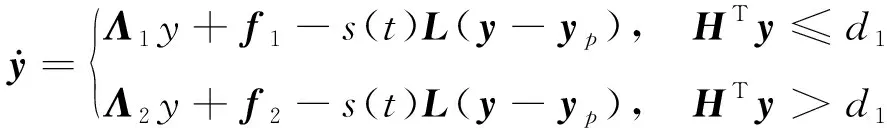
(14)

定義目標系統為

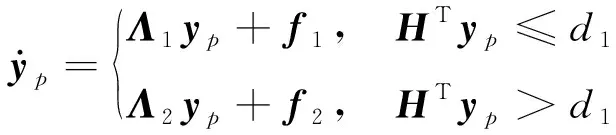
(15)

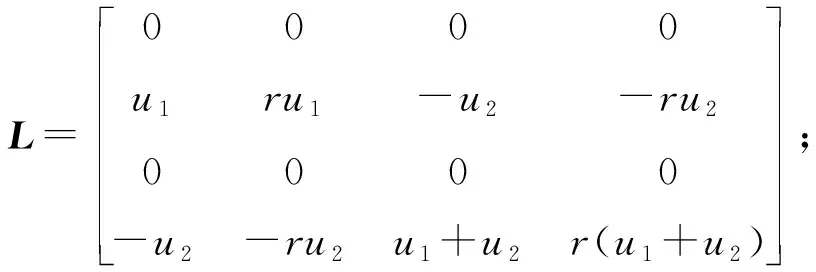
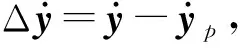
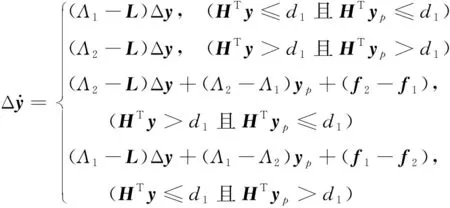
(16)

誤差系統可簡化的表示為

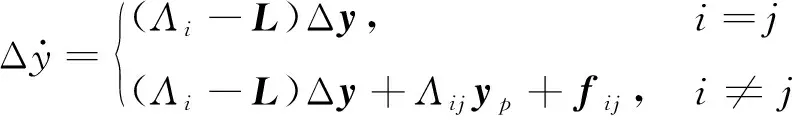
(17)

式中,i,j=1,2,Λij=Λi-Λj,fij=fi-fj。Λi和Λj符合下面的關系

Λi=Λj+GijHT

(18)

式中,Gij∈4×1。將Λi和Λj用向量Gij聯系起來,可防止線性矩陣不等式在求解時出現半負定的情況。

為了證明誤差系統的穩定性,建立如下的Lyapunov函數

V(Δy)=ΔyTPΔy,P=PT>0

(19)

由于目標系統和被控系統自身存在各個向量場之間的相互切換,為了降低保守性,在誤差系統穩定性分析過程中,基于Lyapunov函數來構造穩定性條件;為了進一步降低保守性,將向量場信息通過S-procedure考慮進穩定性條件,使得式(19)所示的Lyapunov函數為正定以及其微分為負定的性質不需要在整個狀態空間內成立,而只需要在對應的向量場內成立即可。

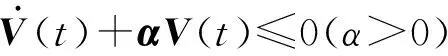
ΔyT[(Λi-L)TP+P(Λi-L)+αP]Δy≤0

(20)

當[(Λi-L)TP+P(Λi-L)+αP]≤0時,可保證式(20)成立。

若被控系統和目標系統分別出處于不同的向量場時有

(HT(yp+Δy)-d1)(HTyp-d1)≤0或

(HTyp-d1)(HT(yp+Δy)-d1)≤0

(21)

式(21)可表示為

(22)

當誤差系統在HTyp-d1≤0且HT(yp+Δy)-d1>0或HTyp-d1>0且HT(yp+Δy)-d1≤0的向量場內,式(22)所示的Lyapunov函數是負定的。根據S-procedure,始終存在常數λ1>0和λ2>0使得下式成立

(23)

結合式(20),可得誤差系統全局穩定的條件(即被控系統的穩定性條件)

當i=j時

ΔyT[(Λi-L)TP+P(Λi-L)+αP]Δy≤0

(24)

當i≠j時

(25)

(26)

式(24)、(25)和(26)是關于{P,L,λ1,λ2}的非線性矩陣不等式,但是關于{P,PL,LTP,λ1,λ2}的線性矩陣不等式。因此,利用線性矩陣不等式的相關求解器可有效地解決這些問題。如果存在矩陣P=PT>0,并且存在正實數λ1與λ2,滿足式(24)、(25)和(26),則誤差系統(16)是漸近穩定的,可以實現共存吸引子的轉遷。

5 仿真研究與分析

5.1 系統共存吸引子產生及湮滅分析

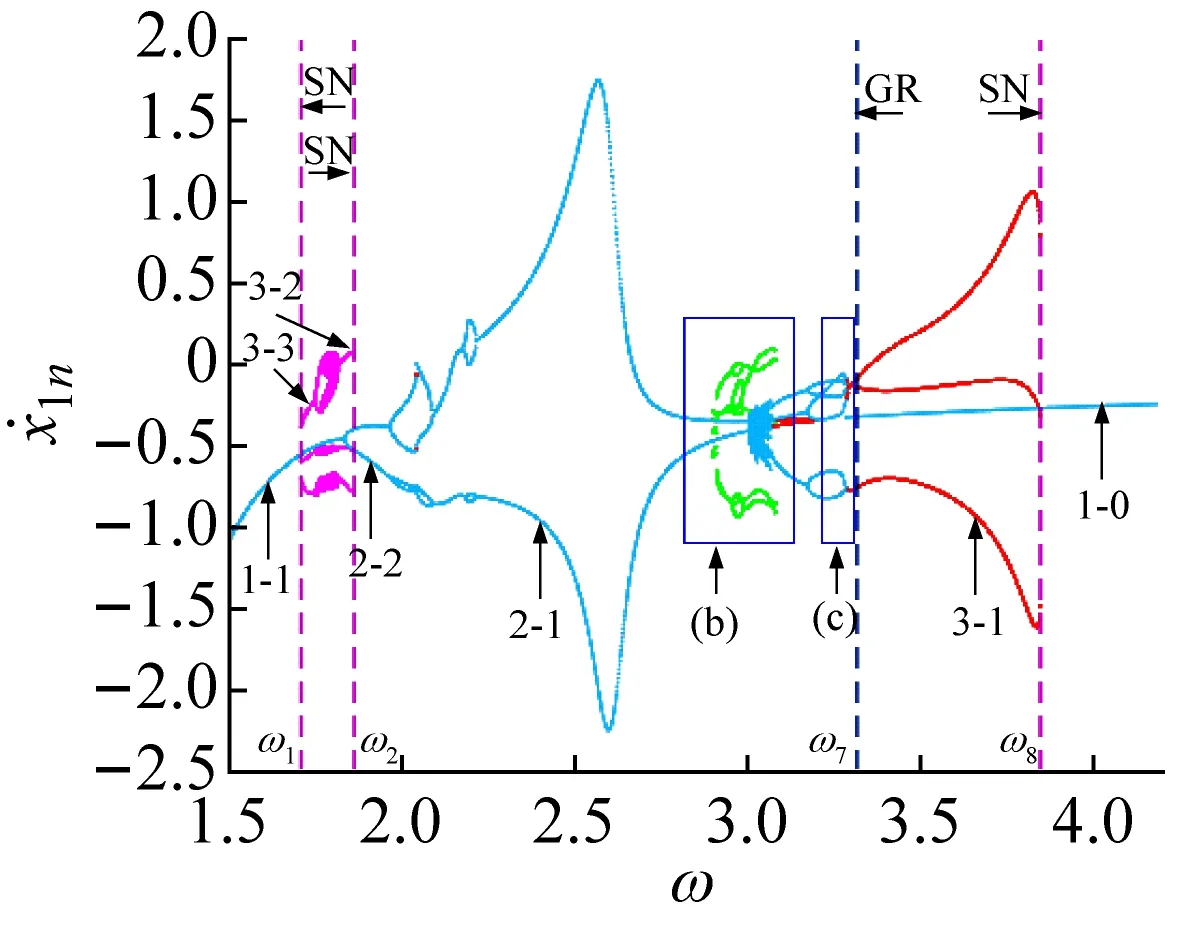
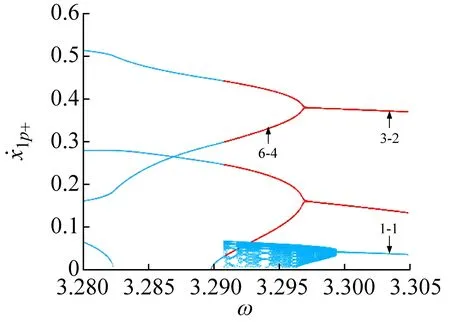
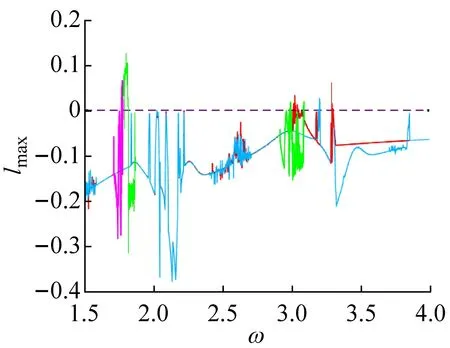
取基準參數①:ω∈[2,3.5],μm=0.5,ξ=0.1,μk2=0.7,μk3=0.95,d1=0.1,μc=0.5,f20=0,結合胞映射方法,可數值仿真得到在狀態平面上系統的分岔圖和Lyapunov指數圖,如圖2所示。圖中用不同的顏色表示共存的不同吸引子或分岔分支,每個分岔分支及其對應的Lyapunov指數變化曲線用相同顏色表示。

(a)

(b)

(c)

(d) 圖2(a)對應的Lyapunov指數圖

(e) 圖2(b)對應的Lyapunov指數圖

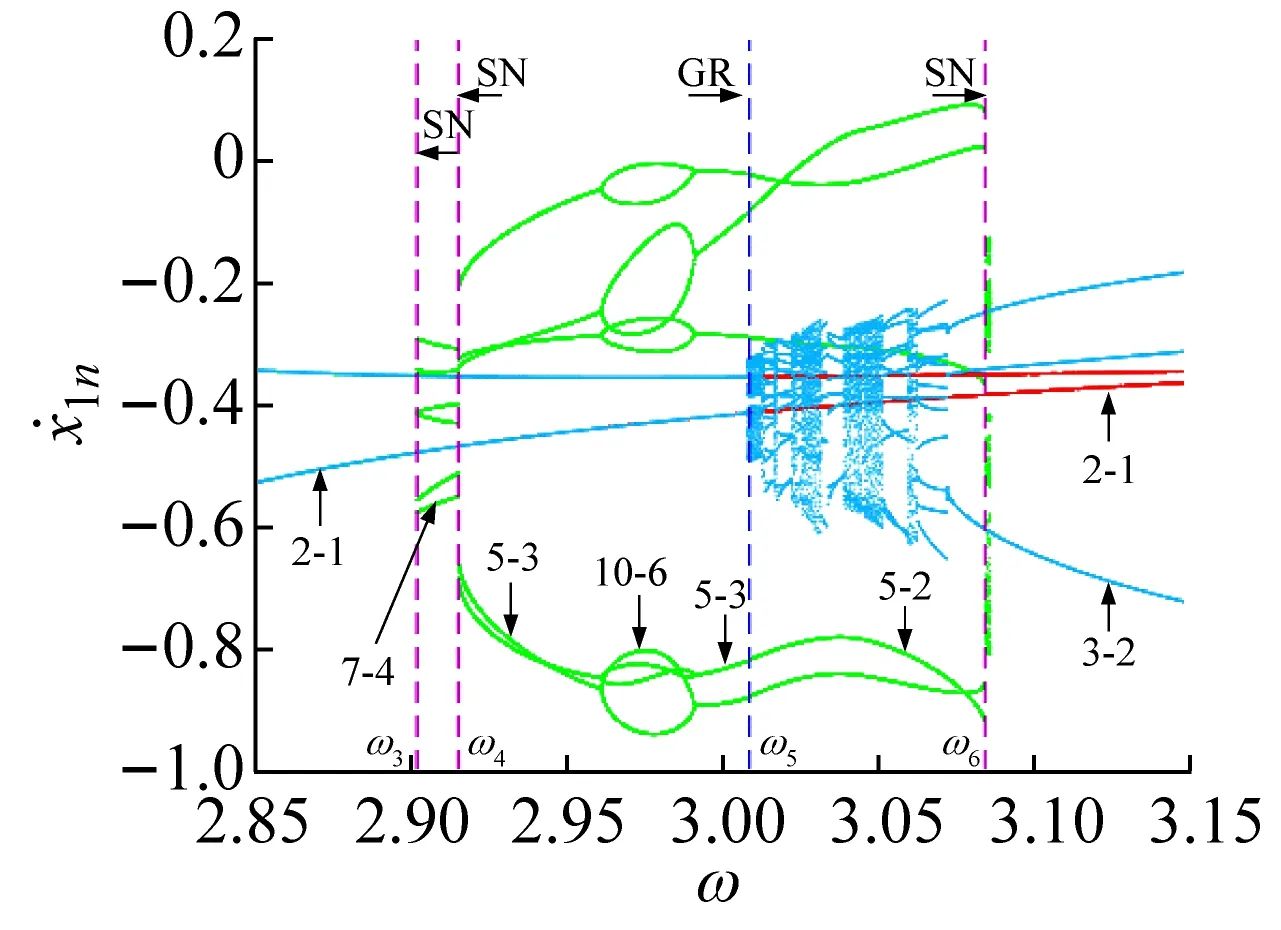
(f) 圖2(c)對應的Lyapunov指數圖圖2 系統的多初值分岔圖和Lyapunov指數圖Fig.2 Global bifurcation and corresponding Lyapunov exponents with multi-initial points

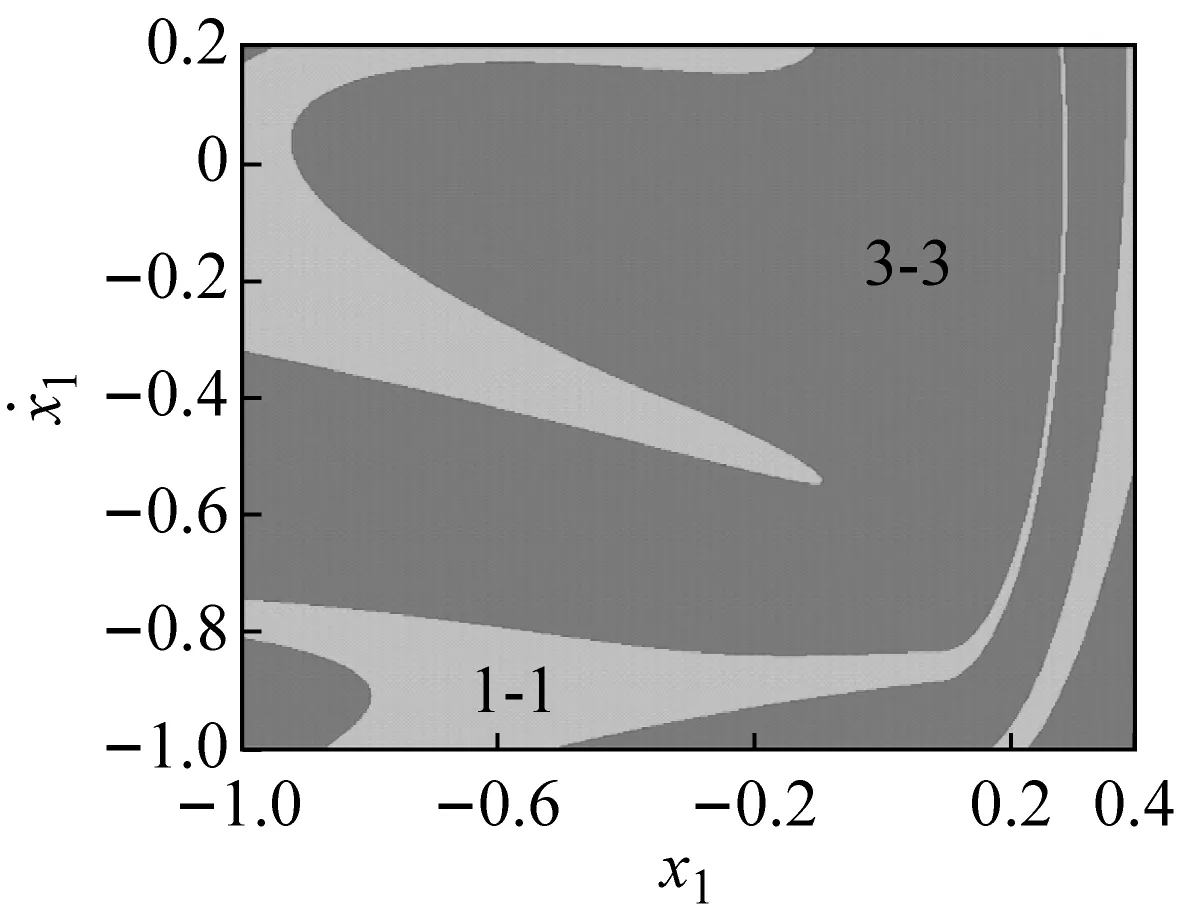
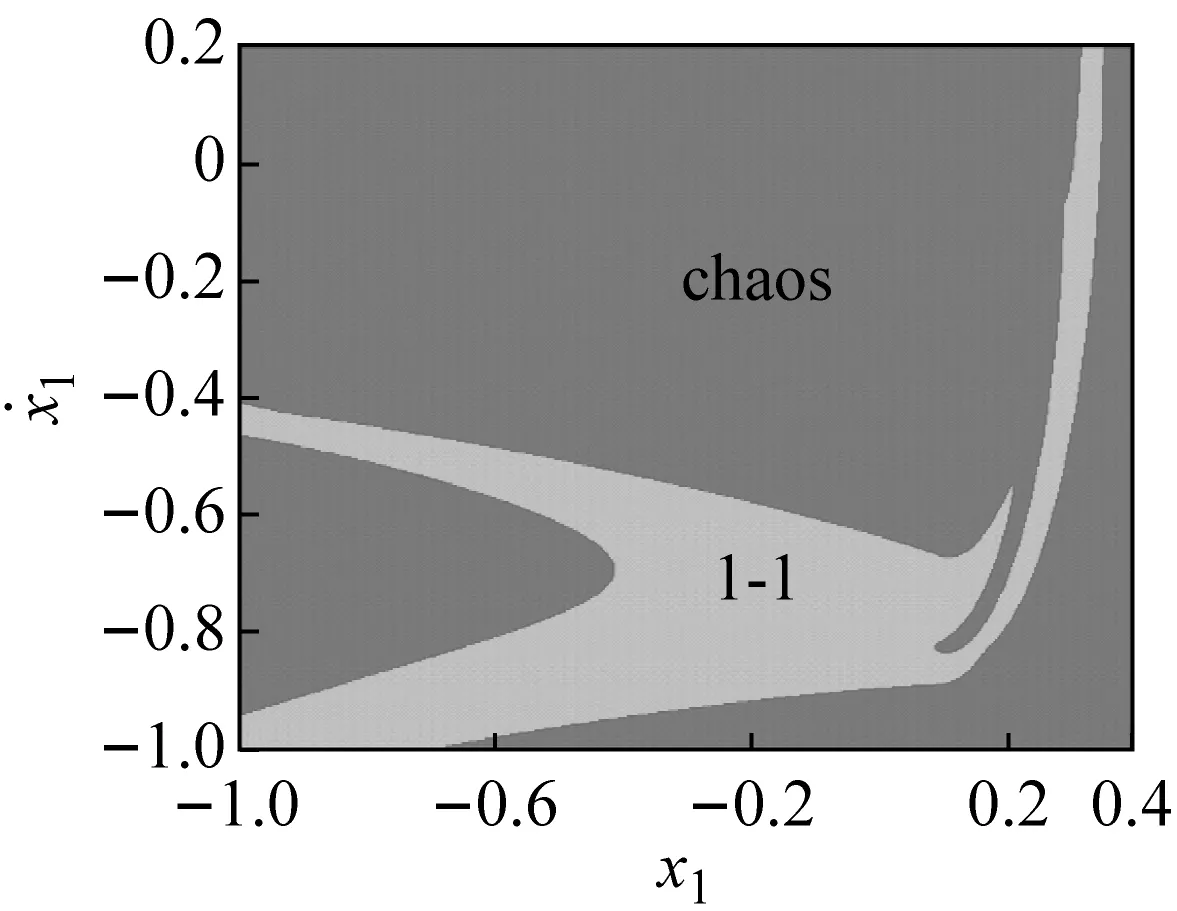
激勵頻率在ω∈[ω1,ω2]區間內變化時,主要存在1-1與3-3周期運動(吸引域分布如圖3(a)所示)、1-1周期運動與混沌運動(吸引域分布如圖3(b)所示)以及3-2與2-2周期運動共存等。在此區間內系統的多態共存區之間主要以倍周期分岔進行轉遷。在ω=ω2處,3-2周期運動的特征值為:λ1=0.999 923,|λ2,3,4|<1;若ω繼續增大,3-2周期運動經鞍結分岔轉遷為2-2周期運動,共存現象隨即消失。在ω1處,3-3周期運動的特征值為:λ1=1.000 196,|λ2,3,4|<1;若ω減小,3-3周期運動經鞍結分岔轉遷為1-1周期運動,共存現象隨即消失,系統只存在1-1周期運動。

(a) ω=1.740 3

(b) ω=1.740 5

(c) ω=3.086 0

(d) ω=3.500 7

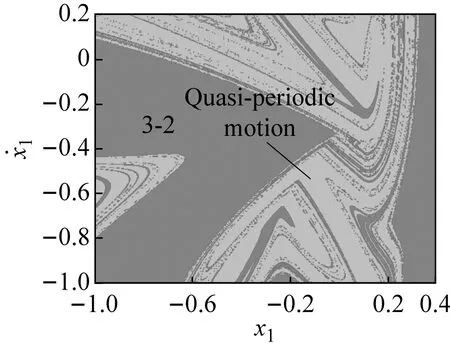
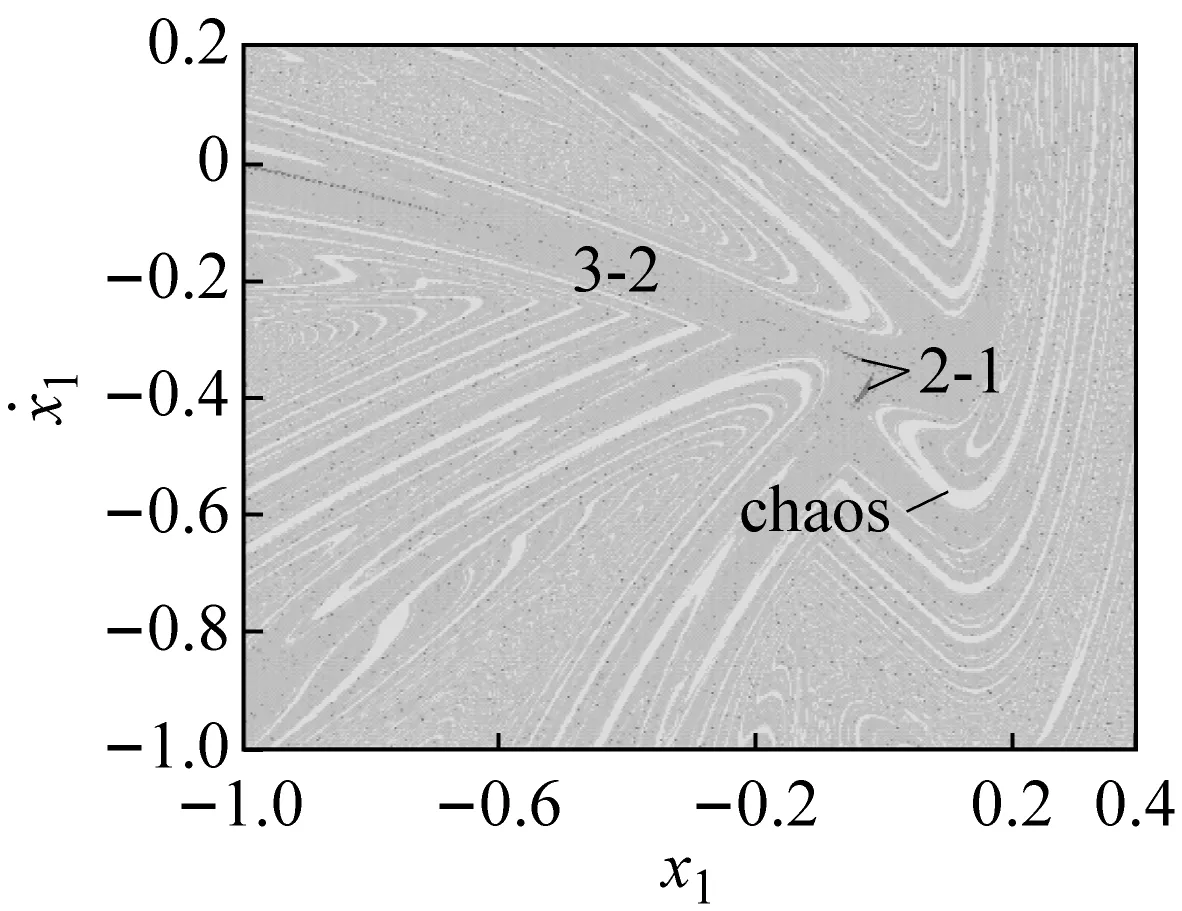
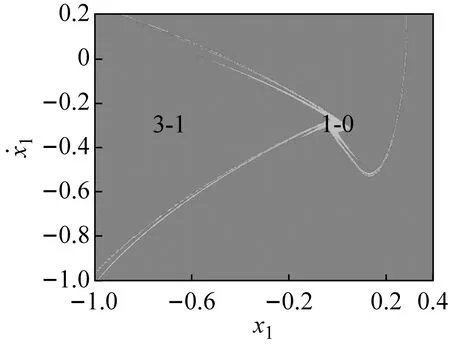
(e) ω=2.298 0圖3 吸引域圖Fig.3 Basins of attraction of the system

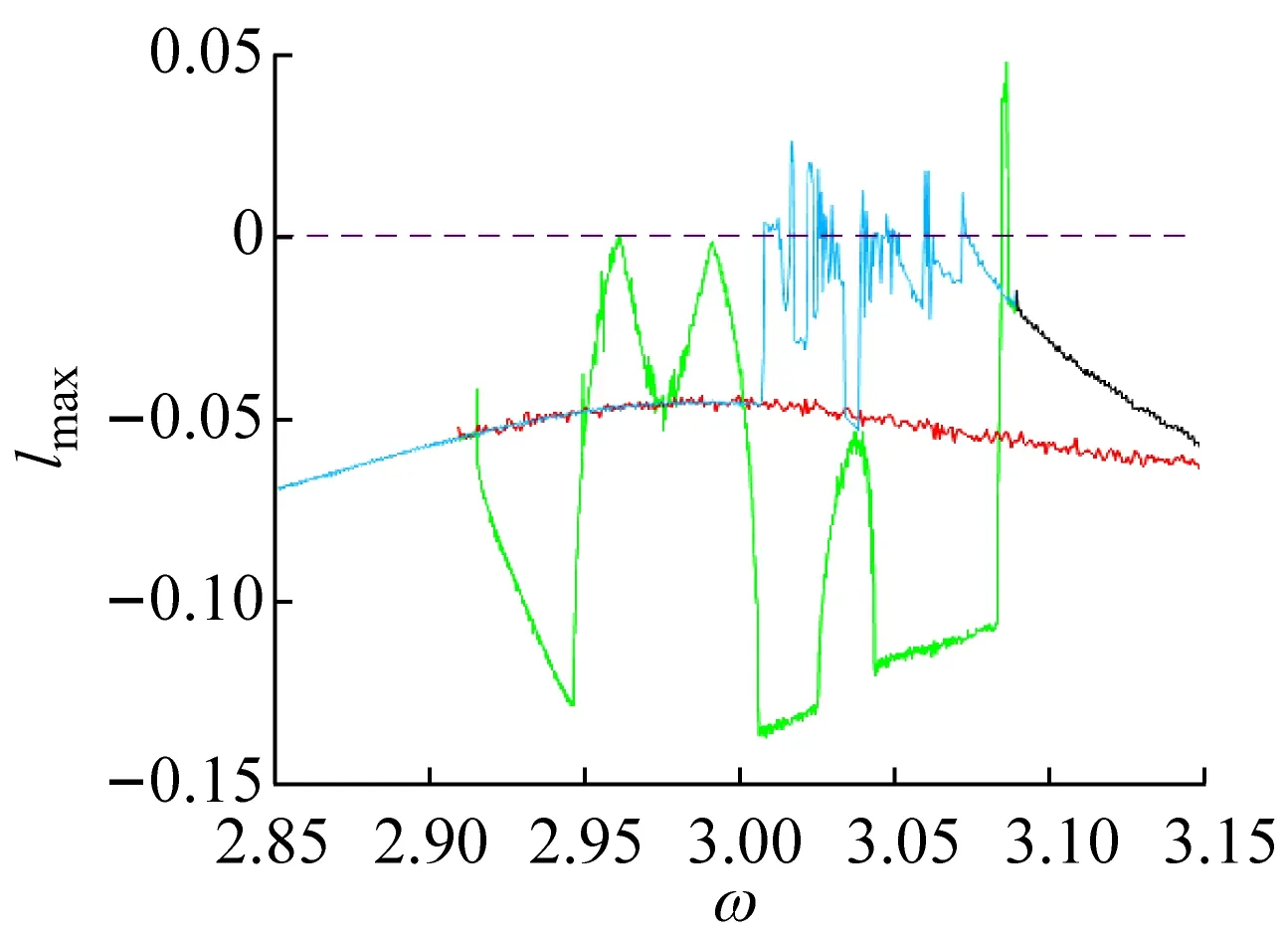
在ω∈[ω3,ω6]區間內,由于對初始狀態的敏感性,隨著ω的遞減,在狀態平面上系統的分岔圖依次存在三個和兩個分支,不同的分支在一些特殊分岔點處會進行轉遷或合并,從而造成多態共存區的轉遷或消失。在ω=ω4處,若ω減小系統發生擦邊分岔,5-3周期運動轉遷為7-4周期運動;在ω=ω5處,若ω增大系統發生擦邊分岔(擦邊相圖如圖4(a)所示),5-3周期運動轉遷為5-2周期運動。在ω4和ω5處擦邊分岔未對共存吸引子的個數產生影響,但實現了不同共存區的轉遷。在ω=ω3處,7-4周期運動的特征值為

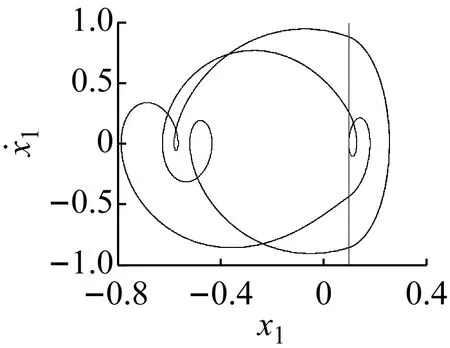
(a) 5-2擦邊周期運動

(b) 1-0和3-1擦邊周期運動圖4 系統擦邊運動的相圖Fig.4 Phase plane of grazing motion

λ1=1.000 043,|λ2,3,4|<1。

若ω減小,系統將發生鞍結分岔,7-4周期運動轉遷為2-1周期運動,從而7-4周期運動所在的分支和2-1周期運動所在的分支合并,系統僅存在2-1周期運動,共存現象隨即消失。

在ω=ω6處,5-2周期運動的特征值為

λ1=1.000 065,|λ2,3,4|<1。

若ω增大,系統將發生鞍結分岔,5-2周期運動轉遷為混沌運動(從圖2(f)所示的Lyapunov指數圖可觀察到),從而形成混沌運動、2-1和3-2周期運動共存的多態共存區(吸引域分布如圖3(c)所示);隨著ω的繼續增大混沌吸引子與其吸引域邊界發生碰撞出現邊界激變造成混沌吸引子的消失,之后系統中只保留2-1和3-2周期運動共存。類似的邊界激變現象在ω5附近也可以觀察到,此處3-2周期運動所在的分支隨著邊界激變的發生而消失,之后系統中僅存在5-3和2-1周期運動共存。

在ω=ω8處,3-1周期運動的特征值為

λ1=1.000 187,|λ2,3,4|<1。

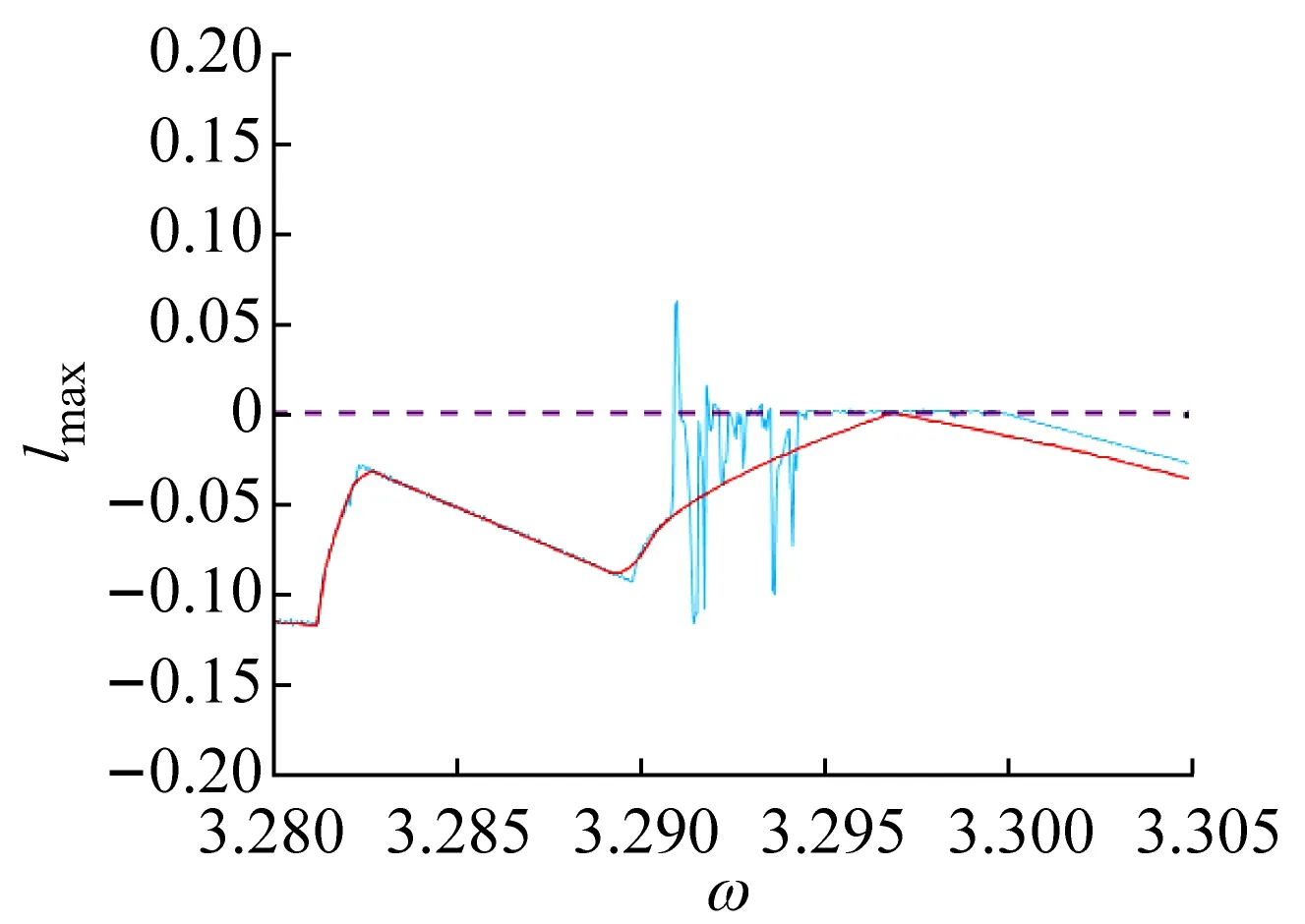
若ω增大,系統將發生鞍結分岔,3-1周期運動轉遷為1-0周期運動,系統吸引子共存現象也隨之消失,系統中只保留1-0周期運動(如圖2(a)所示)。若ω繼續減小,共存的3-1與1-0周期運動(吸引域分布如圖3(d)所示)在不同的初始條件下同時發生擦邊分岔(擦邊相圖如圖4(b)所示),轉遷為3-2與1-1周期運動的多態共存區;隨著ω持續減小,1-1周期運動發生Hopf分岔(在ω=3.298處系統的特征值為:|λ1,2|=1.000 788,|λ3,4|<1)轉遷為擬周期運動,此時出現擬周期運動與3-2周期運動共存的多態共存區(吸引域分布如圖3(e)所示,結合圖2(g)所示的狀態平面上的Lyapunov指數圖可觀察并驗證);隨著ω的繼續減小擬周期運動最終進入混沌運動,并且由于邊界激變造成混沌吸引子消失,共存現象隨即消失。

5.2 系統共存吸引子轉遷驗證分析

通過上面數值仿真發現,在某些參數條件下,圖1所示系統因對初始狀態的敏感性,會穩定運行于若干個不同的吸引子上。針對圖1所示系統對初始狀態的敏感性,以系統共存的某一個吸引子對應的軌道作為目標軌道,而另一吸引子對應的軌道作為被控軌道,通過施加線性反饋控制器,對被控軌道進行力驅動,從而實現吸引子之間的轉遷。

取控制參數r=1、u1=5和u2=5,其余參數均為基準參數①,通過Matlab的YALMIP工具包對式(24)、(25)和(26)進行求解,可得為保證控制的穩定性而增加的帶有約束條件的參數

P(i,i)>0(i=1,2,3,4),det(P)=5.038 6>0;

λ1=16.899 6>0;λ2=16.394 7>0。

由于上述參數的解都符合假定的約束條件,所以在此控制參數下可以實現系統不同吸引子之間的轉遷。

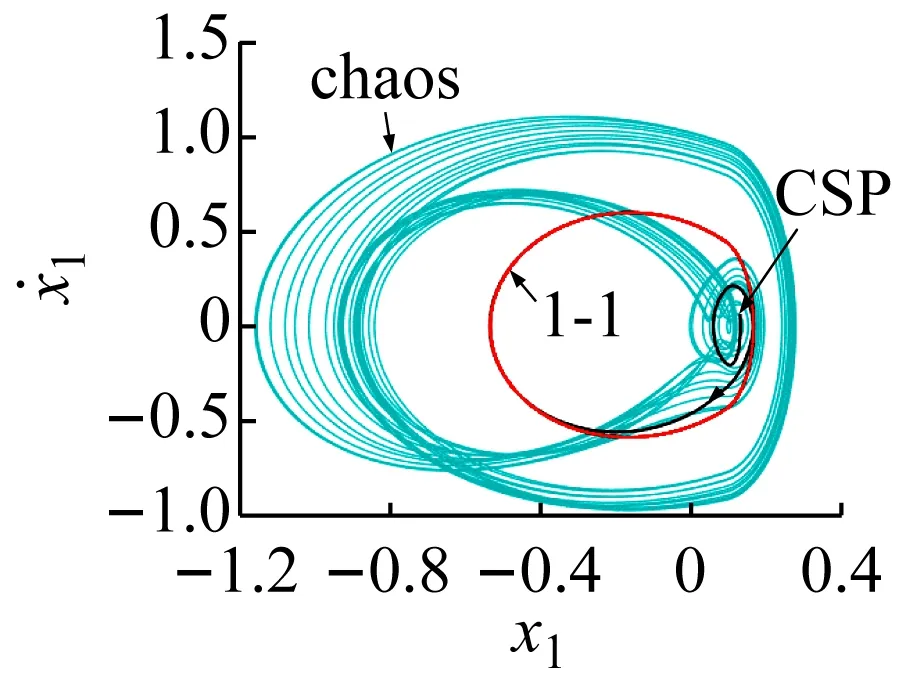
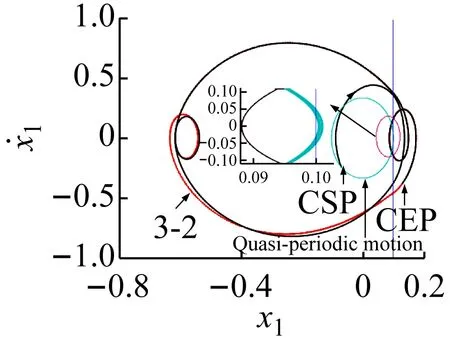
在軌道轉遷的過程中,紅色軌線代表目標軌道,黑色的軌線代表控制過程,淡藍色軌道代表被控軌道。當e(t)<ε(e(t)為被控和目標軌道之間的距離,ε為控制精度,設置為0.000 01)時令s(t)=diag(0,0)控制退出,此時系統可成功轉遷到目標周期軌道。在不同吸引子轉遷的效果圖中用以下符號表示控制的不同狀態:控制開始位置(control start position, CSP);控制結束位置(control end position, CEP);控制開始時間(control start time, CST)。

通過數值方法對上述控制方法和參數進行驗證。由前面的分析結果可知,在ω=1.740 3時3-3周期運動與1-1周期運動共存。將3-3周期運動軌道作為被控軌道,而1-1周期運動軌道作為目標軌道,在3-3與1-1周期運動軌道之間距離最小時施加控制,如圖5所示。圖5(a)、(b)、(c)和(d)分別為將3-3周期運動轉遷至1-1周期運動時的相圖和位移、反饋控制力和控制誤差的時間歷程圖。結合圖5(d)可看出,當控制未施加時系統被控軌道和目標軌道之間的距離變化具有周期性,被控系統會穩定運行在振幅較大的3-3周期運動上。結合圖5(a)、(b)、(c)可看出,當施加控制后,被控軌道在線性反饋控制力的作用下快速向目標軌道遷移,且反饋輸入力和控制誤差會隨著被控軌道和目標軌道之間距離的減小而逐漸減小;在控制施加前和控制完成后,線性反饋控制力都為零,說明此種方法不需要能量的持續輸入。在實際系統中,還需考慮是否限制控制器輸入的上限值,若控制器輸入比較大時,直接施加如此大的一個反饋控制力可能會對系統產生不利的影響或者損壞控制器。

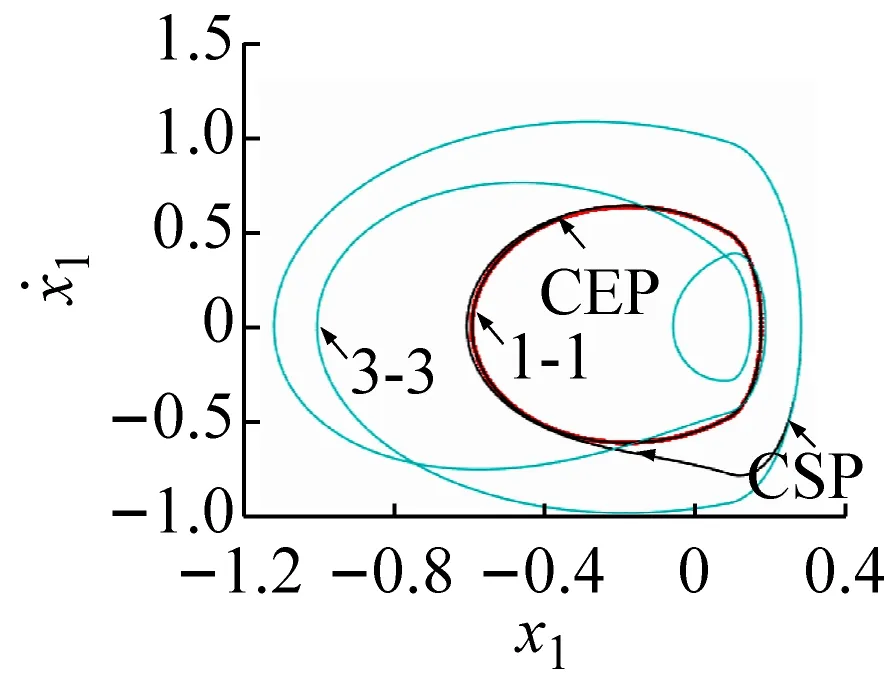
(a) 相軌跡轉遷過程

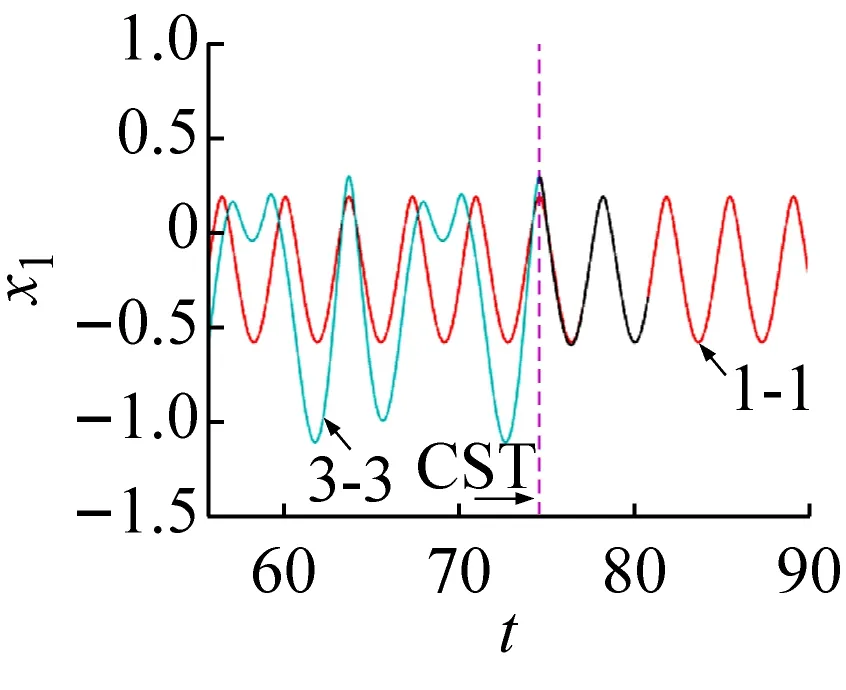
(b) 位移轉遷過程

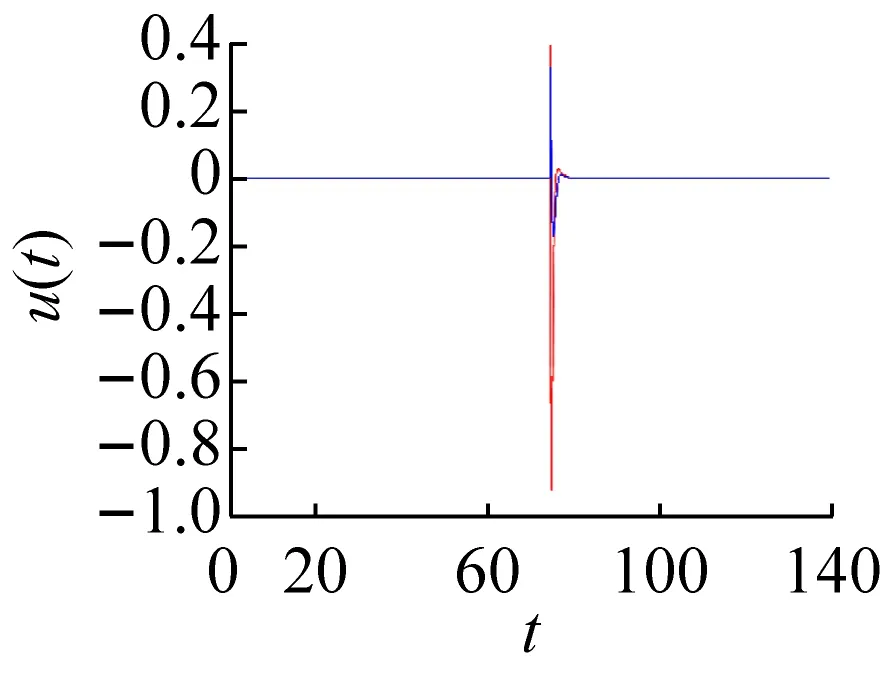
(c) 反饋控制力的時間歷程圖

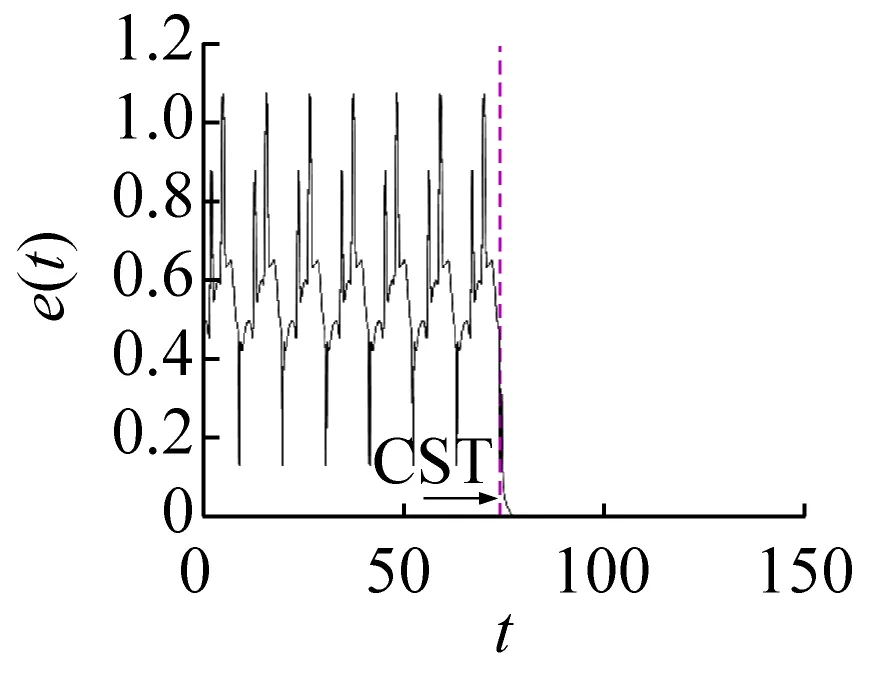
(d) 控制誤差時間歷程圖圖5 3-3周期運動轉遷至1-1周期運動的效果圖Fig.5 The effect chart of 3-3 periodic motion migrating to 1-1 periodic motion

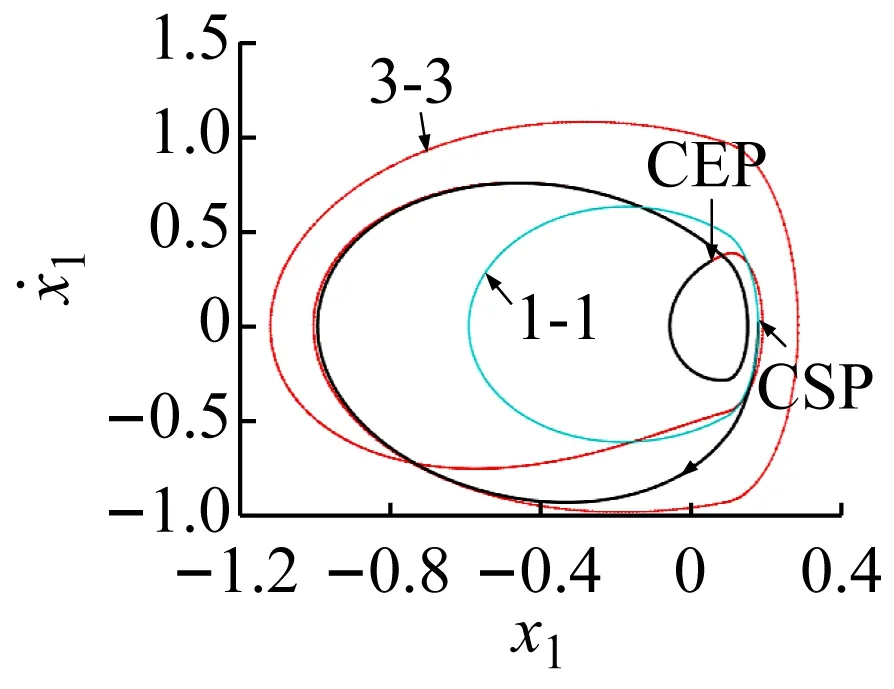
將1-1周期運動轉遷至3-3周期運動的過程如圖6所示;將混沌運動轉遷至1-1周期運動過程如圖7所示;將擬周期運動轉遷至3-2周期運動的過程如圖8所示;將1-0周期運動轉遷至3-1周期運動的過程如圖9所示。

(a) 相軌跡轉遷過程

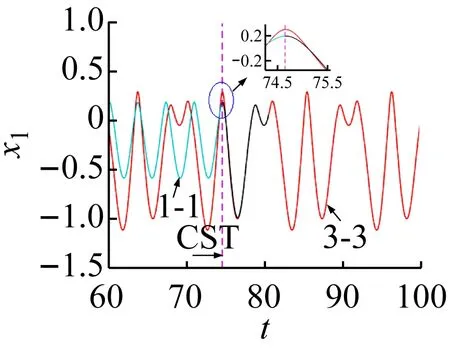
(b) 位移轉遷過程圖6 1-1周期運動轉遷至3-3周期運動的效果圖Fig.6 The effect chart of 1-1 periodic motion migrating to 3-3 periodic motion

(a) 相軌跡轉遷過程

(b) 位移轉遷過程圖7 混沌運動轉遷至1-1周期運動的效果圖Fig.7 The effect chart of chaotic motion migrating to 1-1 periodic motion

(a) 相軌跡轉遷過程

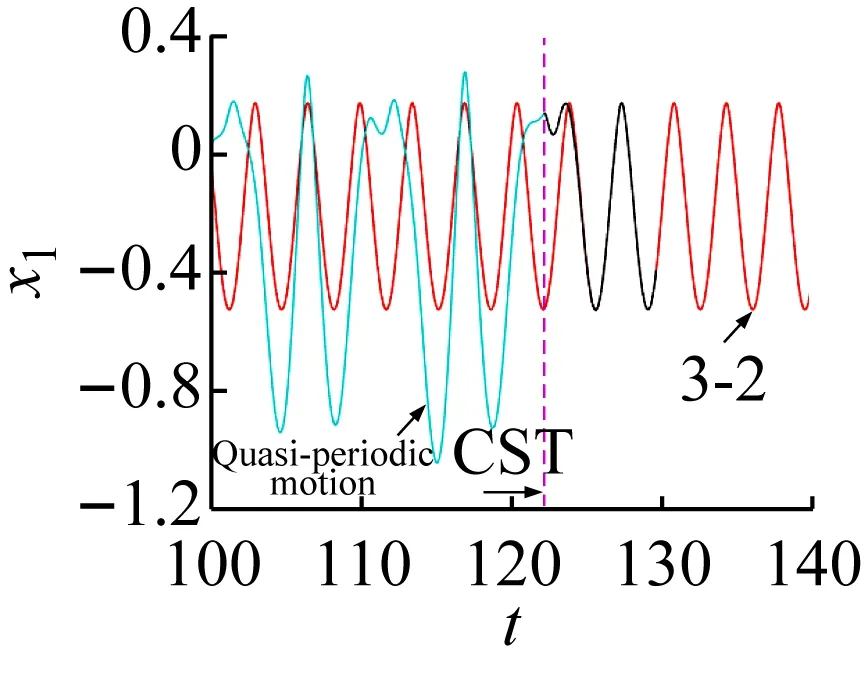
(b) 位移轉遷過程圖8 擬周期運動轉遷至3-2周期運動的效果圖Fig.8 The effect chart of quasi-periodic motion migrating to 3-2 periodic motion

(a) 相軌跡轉遷過程

(b) 位移轉遷過程圖9 1-0轉遷至3-1周期運動的效果圖Fig.9 The effect chart of 1-0 periodic motion migrating to 3-1 periodic motion

由上述仿真結果可見,利用本文方法能夠很好地實現對系統共存吸引子之間的相互轉遷。上述周期運動之間的相互轉遷,不僅可調整系統與約束面的關系,使系統按照不同的使用要求工作;當激勵頻率正向或反向迭代時還可控制各種分岔的發生;將混沌運動轉遷周期運動,可實現對混沌運動的控制。

在控制過程中,控制開始狀態的設置需考慮目標軌道和被控軌道之間距離對控制效果的影響,當目標軌道和被控軌道之間距離較大時施加控制,則在控制初始時刻系統的狀態會出現較大的跳動,反饋控制力較大,且控制過程持續時間較長;而當目標軌道和被控軌道之間距離較小時施加控制,則在控制初始時刻系統狀態的過渡會比較平穩,反饋控制力最小,且控制過程持續時間也最短。以1-1周期運動轉遷至3-3周期運動為例進行驗證。選取三倍激勵周期內被控軌道和目標軌道之間距離的局部極大值點(B和C)以及全局的最大值點(D)和最小值點(A)(如圖10(a)所示)分別為控制開始狀態進行控制。圖10(b)為反饋控制力的時間歷程圖,表1為不同控制開始狀態下反饋控制力的最大值和控制過程持續時間。從圖10(b)和表1可看出,不同的控制開始狀態需要的反饋控制力和控制過程經歷時間不同,當e(t)最大時需要的控制力最大,控制過程持續時間也最長;而e(t)最小時需要的控制力最小,控制過程持續時間也最短;所以在此類系統的共存吸引子轉遷控制過程中應選擇被控軌道和目標軌道之間距離最小時施加控制。

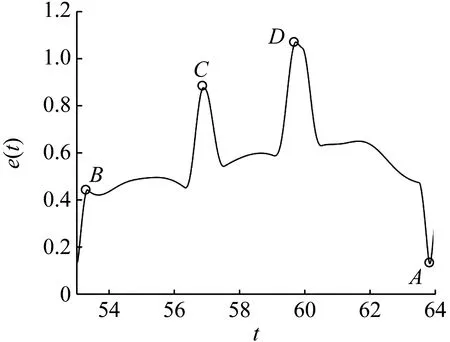
(a) 控制誤差的時間歷程圖

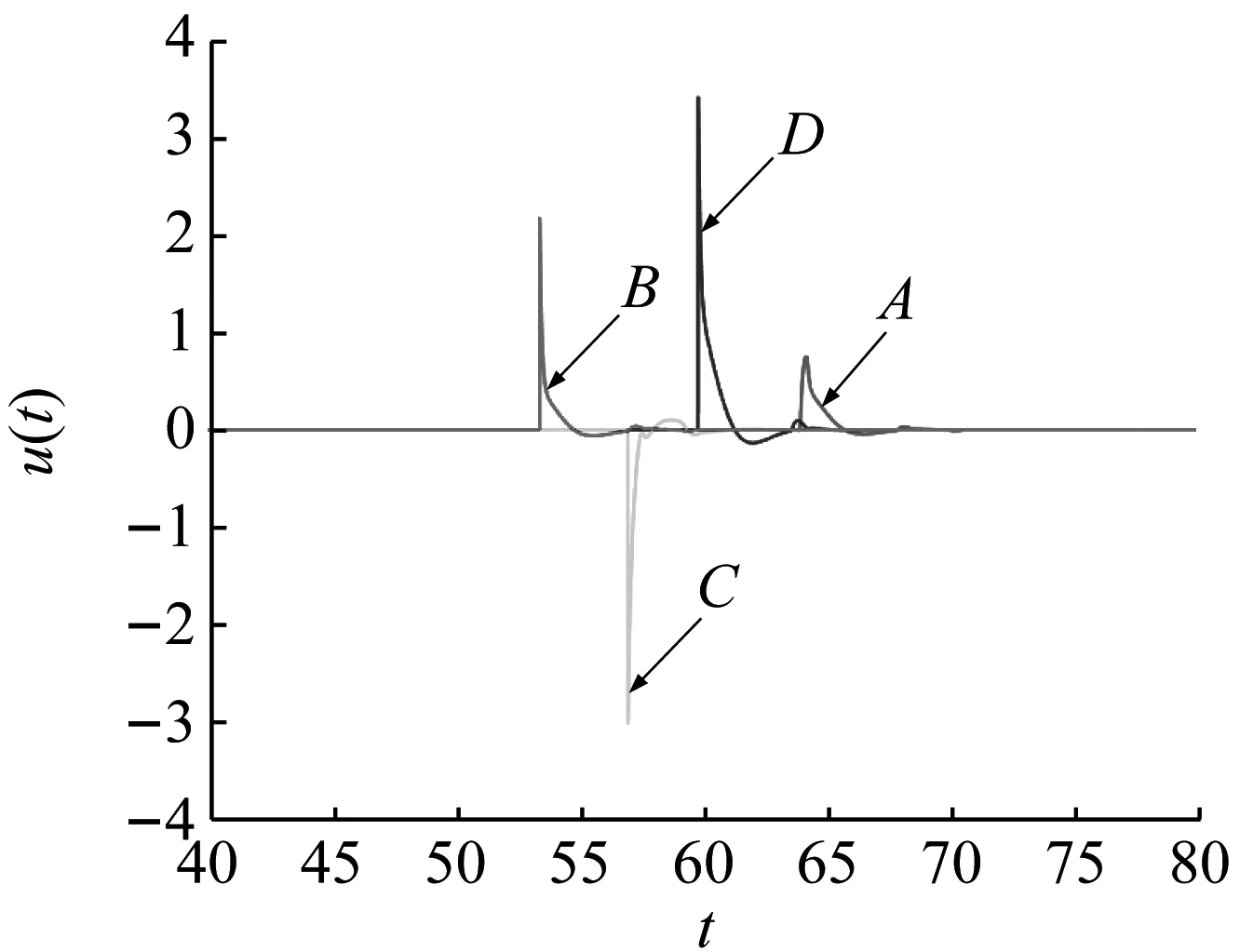
(b) 反饋控制力的時間歷程圖圖10 不同控制開始狀態對反饋控制力的影響Fig.10 The effect of different control starting positions on feedback control force

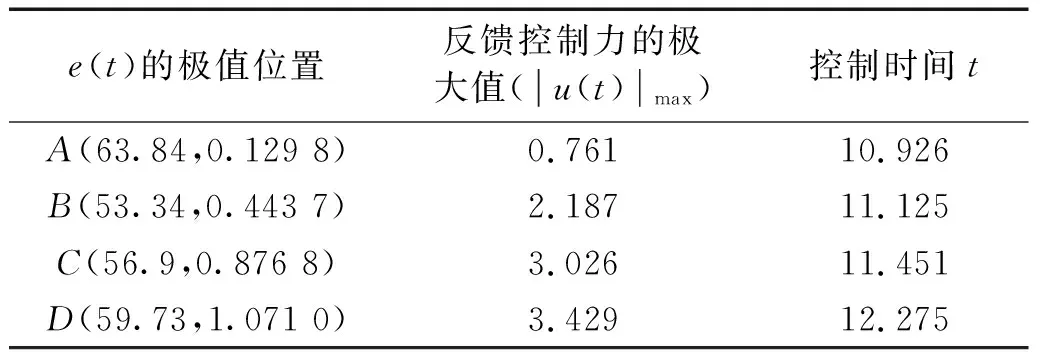
表1 不同控制開始狀態下的控制性能Tab.1 Control performance under different control start states

6 結 論

針對兩自由度含間隙分段線性系統的吸引子共存現象,利用線性反饋控制對共存吸引子實現了相互轉遷,可以得到如下結論:

(1) 相鄰吸引子之間的相互轉遷由系統參數和初始狀態共同決定;鞍結分岔是引起此類系統產生吸引子共存的主要原因,倍周期分岔和擦邊分岔不會對共存吸引子的吸引域結構產生影響,但能實現不同共存區的轉遷,邊界激變是混沌吸引子及其吸引域突然消失的主要原因。

(2) 施加線性反饋控制器后,通過構造二次Lyapunov函數,利用LMI理論并結合系統分段線性的特點,可將被控系統的向量場信息通過S-procedure考慮進穩定性條件,從而將線性反饋控制的穩定性和反饋增益矩陣的選取問題轉化為LMI描述,這樣可解決線性反饋控制在實現分段線性系統共存吸引子轉遷中的穩定性分析及反饋增益矩陣選取問題。

(3) 在此類系統共存吸引子轉遷控制過程中,應選擇被控軌道和目標軌道之間距離最小時開始施加控制。吸引子之間的相互轉遷一方面可使系統工作在理想的周期運動上;另一方面可控制混沌運動的發生,達到提高系統穩定性及減振性能的目的。