數(shù)據(jù)驅(qū)動的復雜電網(wǎng)故障區(qū)域定位方法研究

楊康， 武家森

（1.國網(wǎng)河南省電力公司鄭州航空港經(jīng)濟綜合實驗區(qū)供電公司，河南 鄭州 450000；2.北京中恒博瑞數(shù)字電力科技有限公司，北京 100085）

在“雙碳”目標的引導下，國內(nèi)外大力發(fā)展智能電網(wǎng)技術(shù)，電網(wǎng)結(jié)構(gòu)愈加復雜，電網(wǎng)的運行數(shù)據(jù)量也呈現(xiàn)幾何級增長，明顯具有大數(shù)據(jù)特征［1］。大數(shù)據(jù)技術(shù)在智能電網(wǎng)中的應(yīng)用成為國內(nèi)外研究熱點，亟需研究應(yīng)用數(shù)據(jù)驅(qū)動技術(shù)提高系統(tǒng)穩(wěn)定運行方法［2-3］。如何能在既保證低難度搭建智能電網(wǎng)模型，又能更加準確高效地對系統(tǒng)故障進行定位已成為亟待解決的問題。目前，國內(nèi)外學者針對電網(wǎng)故障區(qū)域定位方法的研究已經(jīng)取得了不少成果，傳統(tǒng)的故障區(qū)域定位方法主要是根據(jù)電壓的特征數(shù)據(jù)判斷故障相對于電能質(zhì)量監(jiān)測裝置的位置，從而確定故障所存在的大體區(qū)域。文獻［4］針對暫態(tài)擾動變量波形，對比其近似度確定短路位置。文獻［5］通過建立新型算法構(gòu)造矩陣，確定故障源的可能發(fā)生區(qū)域。文獻［6］利用觀測點可測區(qū)域、故障節(jié)點位置等判據(jù)實現(xiàn)定位。上述方法受天氣、測量裝置等多種因素影響會產(chǎn)生誤差較大、定位不準確等問題。因此，如何快速、準確地診斷電力系統(tǒng)故障是運行人員最關(guān)心的問題之一［7］。

大數(shù)據(jù)技術(shù)是近年來引起廣泛關(guān)注的一項新技術(shù)。它是指能夠高速捕獲、發(fā)現(xiàn)和分析類型復雜、來源復雜的大量數(shù)據(jù)，并通過經(jīng)濟方法提取其價值的技術(shù)系統(tǒng)［8］。隨機矩陣理論（Random Matrix Theory，RMT），通過對線性特征值統(tǒng)計分析，揭示實際數(shù)據(jù)特征，是數(shù)據(jù)挖掘技術(shù)的典型應(yīng)用；作為一種數(shù)據(jù)驅(qū)動方法，無需建立特定的機理建模［9-10］。因此，RMT 具有對不同電力系統(tǒng)分析適用性、及時性等特點［11］。文獻［12］提出了一種基于傳統(tǒng)同步相量法的故障區(qū)域檢測方法，該方法僅適用于系統(tǒng)故障信號較強時。文獻［13］采用譜分布概率密度函數(shù)的相似度作為狀態(tài)評價的判據(jù)。通過使用連續(xù)、離散小波變換分析瞬態(tài)電壓波形確定故障區(qū)域［14-15］。文獻［16］通過建立增廣矩陣，將平均譜半徑作為評估指標，分析了不同影響因素與評估指標之間的內(nèi)在關(guān)系。由于增廣矩陣包含兩個或多個矩陣之間的統(tǒng)計信息，故可以廣泛應(yīng)用于電力系統(tǒng)中。

針對上述確定故障區(qū)域方法的不足，本文提出基于RMT 和數(shù)據(jù)驅(qū)動的復雜電網(wǎng)故障區(qū)域確定方法研究。利用單環(huán)定理（single ring theory，SRL）對數(shù)據(jù)進行分析，提出以平均譜半徑（mean spectral radius，MSR）作為相關(guān)分析指標確定故障區(qū)域。利用IEEE 39 節(jié)點系統(tǒng)仿真數(shù)據(jù)進行了算例驗證，結(jié)果表明該方法能夠確定系統(tǒng)中故障發(fā)生的區(qū)域。

1 隨機矩陣理論

隨機矩陣理論是一種以統(tǒng)計學為基礎(chǔ)的大數(shù)據(jù)分析方法。通過建立高維隨機矩陣模型，將電網(wǎng)運行數(shù)據(jù)進行矩陣變換，可以準確高效地處理智能電網(wǎng)中復雜的多層級數(shù)據(jù)，利用數(shù)據(jù)特征映射復雜系統(tǒng)的狀態(tài)。將采樣點的時變數(shù)據(jù)視為隨機變量，在系統(tǒng)受小擾動、白噪聲或測量誤差影響時，采樣數(shù)據(jù)會表現(xiàn)出統(tǒng)計特性，因此可以用合適的指標來描述。當系統(tǒng)中存在事件／信號源時，系統(tǒng)中隨機變量的統(tǒng)計特性隨著內(nèi)部運行機制變化而變化。在實際系統(tǒng)運行中，數(shù)據(jù)的維數(shù)會表現(xiàn)出不確定性。但是隨機矩陣的某些特征仍然收斂，并具有一定的精度，這表明隨機矩陣理論能夠應(yīng)用于實際工程中。隨機矩陣的經(jīng)驗譜分布（empirical spectral distribution，ESD）函數(shù)當矩陣維數(shù)趨于無窮大、行數(shù)與列數(shù)之比保持不變時將滿足一些特性。

1.1 圓環(huán)律與M-P 律

式中：c∈（0，1］，c 為常數(shù)。λ 分布在外徑為1、內(nèi)徑為（1-c）2／L的圓環(huán)內(nèi)。

1.2 平均譜半徑

平均譜半徑可用于高維矩陣統(tǒng)計特性的描述。隨機矩陣的平均譜半徑在系統(tǒng)有異常的信號源出現(xiàn)時，動態(tài)過程隨著系統(tǒng)狀態(tài)變化而變化，故常將其作為評估指標。其定義如式（2）所示：

2 復雜電網(wǎng)故障區(qū)域確定方法

為了確定故障發(fā)生的區(qū)域，通過建立增廣矩陣將復雜電網(wǎng)中所有監(jiān)測點中故障擾動數(shù)據(jù)作為狀態(tài)數(shù)據(jù)矩陣，并將各個監(jiān)測點故障擾動數(shù)據(jù)作為增廣部分建立增廣矩陣。根據(jù)隨機矩陣理論分析增廣矩陣與狀態(tài)矩陣的相關(guān)性，相關(guān)性越高，表明該監(jiān)測點更有可能與擾動區(qū)域接近，從而實現(xiàn)故障區(qū)域的確定。

2.1 數(shù)據(jù)處理

假設(shè)在復雜電網(wǎng)中，選擇l 個節(jié)點的量測數(shù)據(jù)作為樣本空間，監(jiān)測每個節(jié)點k 個關(guān)鍵狀態(tài)變量共形成N＝l×k 個狀態(tài)變量。在采樣時刻ti，所測量數(shù)據(jù)構(gòu)成一個列向量，如式（3）所示：

將各個采樣時刻的量測數(shù)據(jù)按照時間序列排列為一個狀態(tài)數(shù)據(jù)矩陣，如式（4）所示：

采用實時分離窗法采集數(shù)據(jù)并進行分析以便進行實時計算，窗口寬度T，在采集i 時刻數(shù)據(jù)時，結(jié)合T-1 時刻數(shù)據(jù)共同形成矩陣：

由于監(jiān)測所得數(shù)據(jù)并不滿足單環(huán)定理所需數(shù)據(jù)要求，需要對原始矩陣x^進行數(shù)據(jù)處理，得到N×T維的非Hermitian 標準矩陣Xˉ：

求取Xˉ的奇異值等價矩陣：

對Z 進行標準化處理得Z：

2.2 構(gòu)建故障區(qū)域定位模型

假設(shè)系統(tǒng)存在p 個監(jiān)測點，進行T 次采樣得到狀態(tài)矩陣Bc∈C（（p×pc）×T）與因素矩陣Bf∈C（（p×pf）×T）。其中狀態(tài)變量pc個，影響因素pf個。

為降低重復數(shù)據(jù)對因素矩陣的影響，需要加入幅值大小為q 的隨機噪聲矩陣N 對影響因素矩陣進一步處理，如式（10）所示：

增廣矩陣如式（11）所示：

利用Bc與N 建立參照狀態(tài)增廣矩陣，如式（12）所示：

在采樣時間t1-t 內(nèi)，定義平均譜半徑差積分［18］：

式中：t1為采樣開始時刻，t 為采樣結(jié)束時刻。

QMSR（t）用來描述不同節(jié)點因素與該采樣時間內(nèi)電網(wǎng)狀態(tài)之間的關(guān)聯(lián)程度。采樣周期內(nèi)QMSR（t）值越大，說明在該節(jié)點系統(tǒng)狀態(tài)受影響越大，節(jié)點所在區(qū)域更有可能成為故障發(fā)生區(qū)域。

2.3 故障區(qū)域定位流程

當電網(wǎng)中某一節(jié)點發(fā)生故障時，故障節(jié)點處數(shù)據(jù)關(guān)聯(lián)程度高于其它節(jié)點，對應(yīng)平均譜半徑縮減程度變高。本文利用系統(tǒng)中模擬的故障線路，進一步確定故障區(qū)域，利用特征值的LMSR.A（t）對故障線路進行區(qū)段選擇。基于RMT 的故障區(qū)域定位方法流程圖如圖1 所示。

圖1 電網(wǎng)故障區(qū)域確定流程圖

3 算例分析

為驗證復雜電網(wǎng)電壓暫降故障區(qū)域定位方法的有效性，應(yīng)用PSCAD 仿真軟件，搭建IEEE-39節(jié)點系統(tǒng)模型，模擬電網(wǎng)電壓暫降故障以獲取數(shù)據(jù)，其結(jié)構(gòu)如圖2 所示。所取滑動時間窗大小40×110，為驗證本文所提方法的有效性。

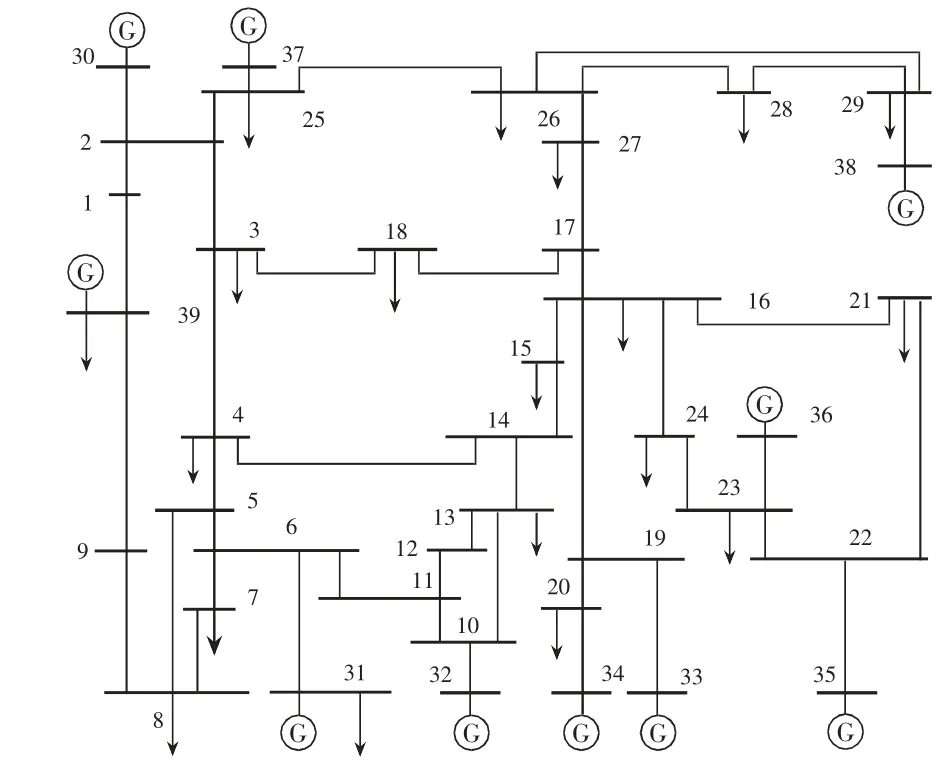
圖2 IEEE-39 標準節(jié)點系統(tǒng)

場景一：設(shè)置節(jié)點11 和節(jié)點14 之間在t＝6s 時發(fā)生短路故障，t＝6.5s 時故障消除。

場景二：設(shè)置節(jié)點34 和節(jié)點35 之間在t＝6.2s時發(fā)生故障，在t＝6.7s 時故障消除。取所有節(jié)點電壓幅值數(shù)據(jù)構(gòu)造狀態(tài)矩陣。

分別利用單環(huán)定理與M-P 律比較故障數(shù)據(jù)對系統(tǒng)的影響如圖3、圖4 所示。

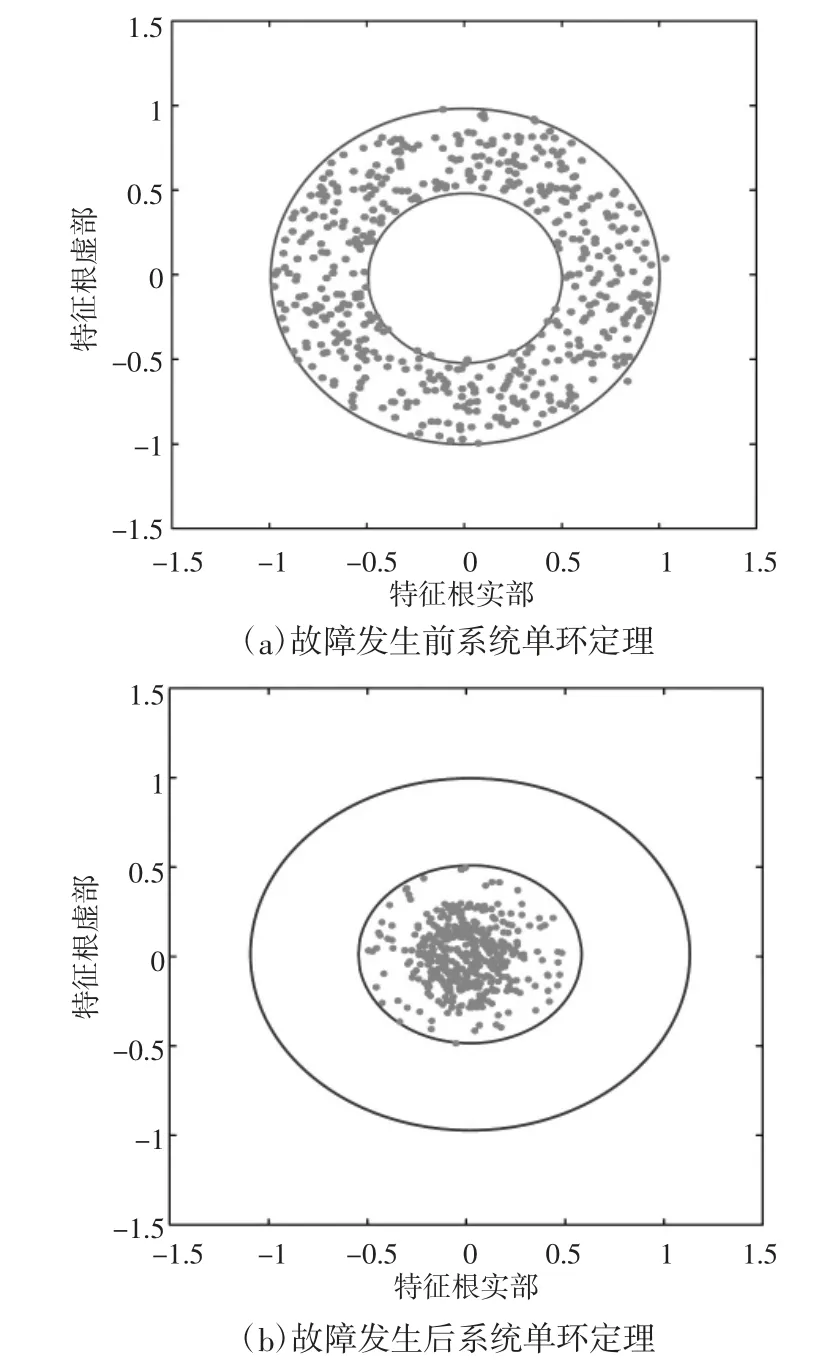
圖3 故障前后單環(huán)定理效果圖

由圖3（a）可知，當系統(tǒng)處于故障發(fā)生前時，狀態(tài)矩陣奇異值點分布在外環(huán)和內(nèi)環(huán)之間，滿足單環(huán)定理，個別外環(huán)點為異常數(shù)據(jù)導致。圖3（b）可知，當系統(tǒng)在故障發(fā)生時刻時，奇異值點集中在內(nèi)環(huán)之內(nèi)，且分布較密集，不滿足單環(huán)定理。

由圖4（a）知，在故障發(fā)生前概率密度分布均勻，滿足M-P 律，系統(tǒng)處于穩(wěn)定狀態(tài)。由圖4（b）知，故障發(fā)生后，系統(tǒng)出現(xiàn)極端特征值，概率密度不均勻分布，不再滿足M-P 律。

針對以上兩個場景，根據(jù)所建立增廣矩陣及參照增廣矩陣求取矩陣QMSR（t）值。部分節(jié)點QMSR（t）值如圖5 所示。

圖5 系統(tǒng)部分節(jié)點分布圖

由圖5（a）可知，節(jié)點11 和節(jié)點14 的QMSR（t）值明顯高于其他節(jié)點，說明故障發(fā)生對這兩個節(jié)點的影響程度要高于其他的節(jié)點，這兩個節(jié)點所在的區(qū)域更有可能為故障發(fā)生的區(qū)域。同理由圖5（b）可知，節(jié)點34 和節(jié)點35 的QMSR（t）值高于其他節(jié)點，說明這些節(jié)點所在區(qū)域更有可能為故障發(fā)生的區(qū)域。

上述分析說明，在系統(tǒng)發(fā)生故障時，單環(huán)定理與M-P 律可以直觀反應(yīng)系統(tǒng)是否穩(wěn)定。因此，本文所提方法能夠較好地實現(xiàn)故障區(qū)域確定。

4 結(jié)論

本文從數(shù)據(jù)驅(qū)動的角度及電網(wǎng)的運行實際情況出發(fā)，提出了一種基于隨機矩陣復雜電網(wǎng)故障區(qū)域的定位方法，通過2 個場景驗證了方法的正確性，得到以下結(jié)論：

（1）復雜電網(wǎng)運行數(shù)據(jù)反映了系統(tǒng)的運行狀態(tài)，傳統(tǒng)分析方法難以分析處理大規(guī)模數(shù)據(jù)量，因此將隨機矩陣理論引入復雜電網(wǎng)分析中，有效利用運行數(shù)據(jù)，可以明顯提高診斷結(jié)果的準確性。

（2）應(yīng)用單環(huán)定理及M-P 律判別電網(wǎng)的運行狀態(tài)，分析狀態(tài)增廣數(shù)據(jù)之間的相關(guān)性，利用增廣矩陣平均譜半徑積分作為評價指標，能夠準確定位故障發(fā)生的區(qū)域。該方法不僅能夠有效降低數(shù)據(jù)矩陣的維數(shù)，還可以更快地分析數(shù)據(jù)。而且不受限于復雜電網(wǎng)的模型結(jié)構(gòu)和運行機制，能夠避免由于物理假設(shè)所帶來的誤差。