基于主成分分析法優化神經網絡的滆湖組黏性土抗剪強度預測

顧春生, 唐鑫, 朱常坤*, 陸志鋒, 劉濤, 張其琪

(1.江蘇省地質調查研究院, 南京 210080; 2.自然資源部地裂縫地質災害重點實驗室, 南京 210080)

近年來,數學方法在地質工程研究領域得到快速發展[1-2];多元回歸算法、套索回歸算法(least absolute shrinkage and selection operator,LASSO)、聚類分析、反向傳播神經網絡(back propagation neural network,BPNN)、因子分析、主成分分析(principal component analysis,PCA)等機器學習算法,在建立特定地質參數的反演預測模型過程中得到廣泛應用[2-4]。呂樹勝等[3]將層次聚類算法運用到了土體分類過程中。李澄清等[4]運用BP模型建立了土體細觀力學參數的反演模型。王晨暉等[5]運用主成分分析法、粒子群算法實現對廣義神經網絡模型的優化,建立了多因素影響下地震震級預測評價模型,為地震震級預測提供參考。韓曉育等[6]運用LASSO算法篩選出目標參量的強相關、非共線性參數,有效提升了伊犁河中長期徑流預報模型的精度。袁穎等[7]運用PCA算法從多個參數中提取影響地裂縫危險性的主成分,消除了解釋變量之間的線性關系,進一步提高了蘇錫常地裂縫危險性預測模型的效率和精度。而神經網絡模型雖在提升模型精度方面效果顯著,但模型可解釋性方面缺陷明顯。LASSO算法在高維度樣本降維方面效果顯著,聚類分析等特征選擇方法在因子重要性分析等領域效果顯著,但運用上述單一方法建立預測模型,預測效果不理想。在數據維度高、信息量大,試驗成本高、指標較難獲得等情況下,適當運用多種數學方法可以顯著提高地質參數預測模型的預測精度、泛化能力以及模型的可解釋性[8]。

土體抗剪強度是邊坡穩定性評價、土壓力計算過程中無法回避的重要指標。為此,學者們對特殊巖土體強度特性開展了研究。王文軍等[9]通過研究淤泥固化土的無側限抗壓強度,并建立了預測模型。范婷婷等[10]研究了砂類土抗剪強度與孔隙比之間的關系,并建立了理論表達式。陳鴻賓等[11]通過土工試驗,總結出了重塑紅黏土含水率、干密度與其抗剪強度參數間的關系。孔令亞等[12]通過室內試驗探究了含水率、夾層厚等因素對巴東地區軟弱巖層強度的影響。蔡國慶等[13]運用統計回歸方法榆林Q3黃土等特殊土體物理力學指標的相關性進行了研究并給出了指標間經驗公式。但上述針對特殊土抗剪強度研究采用的經驗公式及多項式擬合等常規方法均易受異常樣本干擾導致較差擬合效果;當樣本量較大時擬合效果也會顯著降低。

蘇錫常地區滆湖組地層是一種較為典型的土層,其具有埋深淺、強度高、分布廣泛等工程地質特性[14-15],其對區內地下空間開發與地表建筑設計等方面具有重要意義。然而,學者對滆湖組黏性土層的抗剪強度等工程地質特性研究較少。

鑒于此,為了研究蘇錫常地區滆湖組黏性土抗剪強度特性,運用PCA對多維樣本數據進行降維,構建具有非共線特征的主成分,研究個主成分與抗剪強度參數間關系。最終建立基于PCA-BPNN模型的滆湖組黏性土抗剪強度預測模型。為運用數學方法研究土體工程地質參數及海量室內土工試驗數據價值的深度挖掘和利用提供參考。

1 模型概述

1.1 PCA概述

巖土體工程地質參數之間多具有一定相關性[9-13,16];當相關性較強的參數共同作為解釋變量進行參數預測時,預測樣本會包含重疊信息量;而這種解釋變量之間存在較強相關性的特征被稱為多重共線性;當重復選取具有多重共線特征參數時,會提升模型復雜程度,降低計算效率與精度[1,7];甚至造成模型的過度擬合,降低模型泛化能力。而PCA是一種可以將具有相關性的多維自變量進行矩陣變換,簡化構造出低維度、互不相關的新變量,且新變量可以盡可能多地保留原始數據信息的數學方法[17-19]。

在PCA中樣本信息量是用主成分方差來衡量的,主成分方差越大,樣本在此維度下的信息量越大[19]。PCA通過計算主成分貢獻率和累計貢獻率來確定主成分個數;而主成分貢獻率為提取出的主成分方差與原始變量總方差之比[20-21]。具體主成分提取及參數計算過程如下。

步驟1將m個具有n維變量的總體樣本Xnm用矩陣表示為

(1)

步驟2計算協方差矩陣;對樣本數據進行標準化處理,并消除量綱影響;繼而求出樣本各參數的相關系數矩陣R。

步驟3然后根據相關系數矩陣R及其特征方程,按式(2)計算出主成分特征值λi;并按大小進行排序λi≥λi+1≥ 0。

步驟4計算主成分貢獻率和累計貢獻。

|λE-R|=0

(2)

(3)

(4)

式中:E為單位矩陣;p為樣本參數維度;R為n維樣本參數的相關系數矩陣;λi為第i個參數維度對應的主成分特征值;CP為第i個主成分方差貢獻率;ACP為前i個主成分方差累計貢獻率;λl為第l個參數對應的主成分特征值;λk為第k個參數對應的主成分特征值。

步驟5確定主成分數量;求因子載荷矩陣β。建立主成分方程Fi=βi1X1+βi2X2+…+βipXp;由因子載荷矩陣對樣本主成分進行解釋、提取,建立新變量矩陣。最終完成對高維樣本的降維。

此時,新變量可以作為BPNN模型的輸入層;既保留了原始樣本大部分信息,又大大降低了預測模型的復雜程度。

1.2 BPNN模型

BPNN模型是逆向傳播訓練的多層前饋神經網絡,是應用最廣泛的神經網絡模型之一[3-4]。BPNN模型由輸入層、隱含層和輸出層三部分組成;各部分通過權值、偏置值和激活函數相互聯系;根據計算誤差對神經元權值和偏置值進行迭代和修正;最終得到理想的神經元權值參數矩陣的方法,即BPNN模型[20]。

將運用PCA算法篩選出的變量作為 BPNN模型的輸入層;至此,PCA-BPNN模型的結構構架搭建完畢;模型結構如圖1所示。

圖1 PCA-BPNN模型結構圖Fig.1 Structure of PCA-BPNN model

1.3 模型精度評價

為了比較不同模型運行效果,用預測值與樣本真實值的均方根誤差、相關系數進行綜合評價。

(5)

(2)擬合優度(R)。用擬合優度R評價模型效果,R趨近于1,模型擬合的效果越好;R趨向于0,擬合效果越差,R的計算公式為

(6)

2 基于PCA算法的參數分析

2.1 地質背景

滆湖組黏性土層在蘇錫常地區廣泛分布(圖2),是地下空間開發利用、地基與基礎工程建設常涉及的重要工程地層之一。第四系滆湖組地層上段和下段是一套灰色、青灰色、黃灰色、灰黃色的可塑-硬塑,含鐵錳質斑點的黏性土,以粉質黏土和黏土為主的典型黏性土層,具有埋深淺、分布廣、強度高等工程地質特性,為良好基礎持力層[14-15]。

圖2 蘇錫常地區滆湖組黏性土分布圖Fig.2 Distribution map of cohesive clay in Gehu Formation in Su-Xi-Chang area

因此,開展滆湖組黏性土抗剪強度特性研究,對指導蘇錫常地區地下空間開發利用、建筑工程勘察設計等工作具有重要意義。

2.2 滆湖組黏性土工程地質參數統計

研究對象為蘇錫常地區711組滆湖組黏性土室內土工試驗數據,樣本中含有11個解釋變量(表1),2個研究變量(c、φ)。然后對數據進行多參數相關性分析,計算得到樣本各參數相關系數矩陣(圖3);結果顯示:各參數基本服從正態分布,樣本具有較好的代表性。樣本11個解釋變量與黏聚力相關系數均大于0.4,有4個大于0.6;而與內摩擦角的相關系數大于0.4的也有5個;說明各參數單因子建模對抗剪強度的預測水平較低。解釋變量之間存在9組參數兩兩相關系數大于0.8。說明解釋變量內部也存在較強相關性;如重復選取強相關待選參數作為模型因子勢必會造成預測模型的穩定性與精度。因此,消除滆湖組黏性土參數間多重共線性是提高巖土體抗剪強度參數預測模型精度與泛化能力的重要環節。

表1 滆湖組黏性土參數統計Table 1 Parametric statistics of Gehu Formation cohesive soil

圖3 樣本參數概率分布及相關系數熱圖Fig.3 Heat map of probability distribution and correlation coefficient of soil parameters

2.3 基于PCA算法的滆湖組黏性土參數分析

2.3.1 主成分分析過程

運用PCA算法對11組滆湖組黏性土工程地質試驗數據進行變換,求取特征值;得到的主成分特征值λ1=5.73,λ2=4.03,λ3=0.52;其余主成分特征值均小于1;說明第一、二主成分對原樣本的解釋力度優于原變量的平均解釋力度;第三主成分解釋力度已大幅降低,其余主成分解釋力度依次降低(圖4),從而確定主成分數量不大于3個。此時,第一主成分貢獻率為52.1%;當主成分維度為2時,累計貢獻率達到88.8%;當主成分維度為3時,累計貢獻率為93.5%(圖4);此時參數維度得到大幅降低,即能保留樣本大部分信息量,又避免了參數之間的多重共線性。

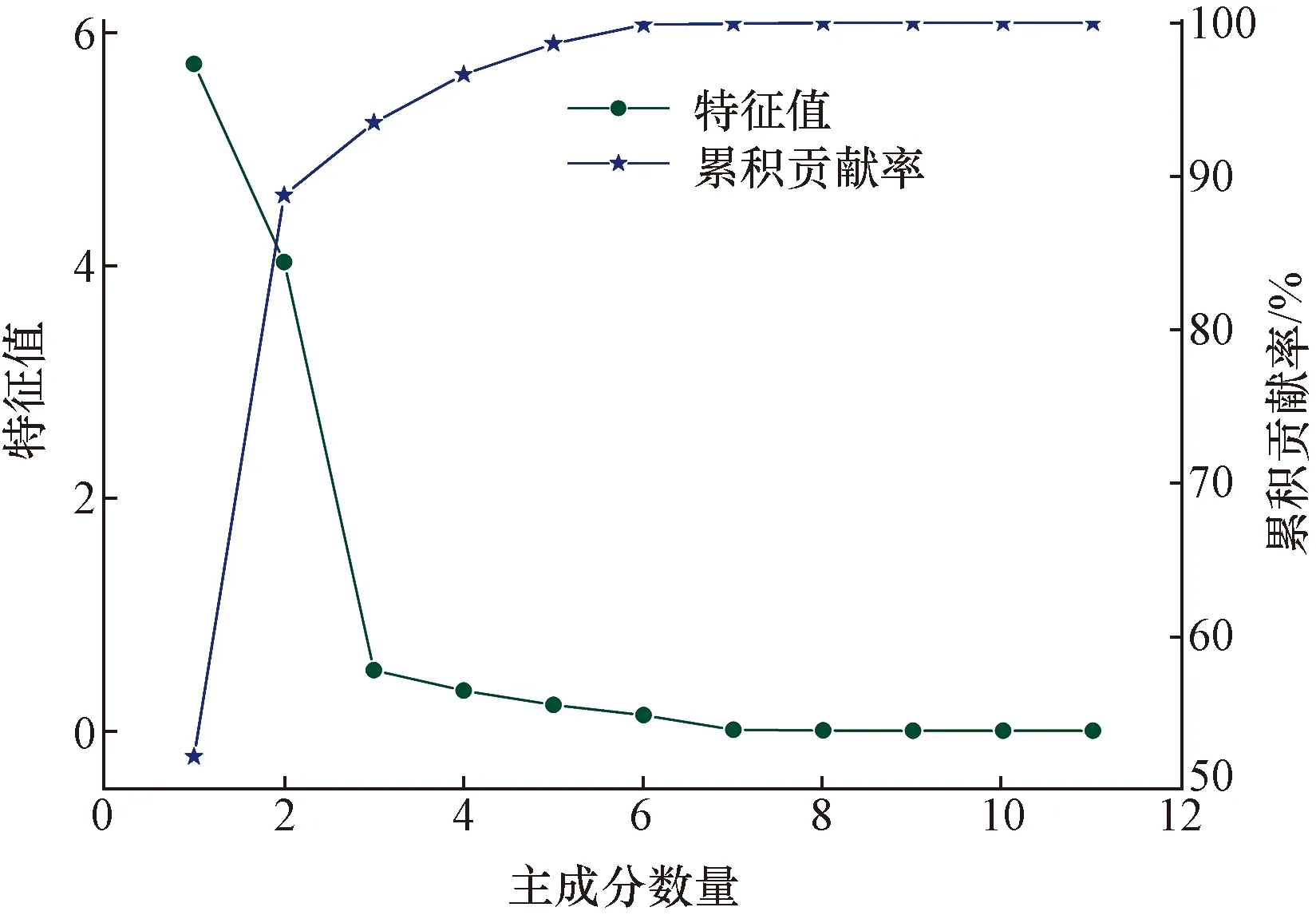
圖4 PCA碎石圖Fig.4 Stone map of principle components

通過主成分得分散點圖(圖5)可知,黏土與粉質黏土散點分布,均在PC1方向上具有較大方差;粉質黏土和黏土樣本未出現較為顯著的分類;因此,僅從已有樣本數據出發,滆湖組黏性土沒有必要對粉質黏土與黏土單獨建立預測模型。根據圖5中主成分參數荷載可得:兩組原參數(e0、w)與(γ、γd、γsat)組內參數在載荷圖中位置幾乎重疊,說明組內參數含有較多相似信息;并呈現組內正相關,組間負相關關系。結合表2中各主成分得分系數,參數(e0、w)與(γ、γd、γsat)的得分系數相對較大,說明這兩組參數對第一主成分貢獻顯著。

表2 主成分得分系數Table 2 Coefficient of principal component score

藍線為參數載荷圖5 主成分得分散點與參數荷載圖Fig.5 Score plot of principal component and parameter load diagram

從第一、二主成分中主要變量e0、w、γ的樣本三維散點圖(圖6)可知,隨著孔隙度越大,天然含水率越高,天然重度與飽和重度等越低的規律。說明第一主成分綜合反映了滆湖組黏性土孔隙特征、含水率特性。同理,第二主成分中參數wl、wp、IP、等具有較大貢獻;綜合反映了滆湖組黏性土中塑液限等參數之間的相互影響趨勢,并將第二主成分歸納為滆湖組黏性土的水穩特性。

滆湖組黏性土含水率、孔隙度、天然重度三參數之間均存在較強線性關系[圖6(a)];塑液限、塑性指數三參數間也存在較強線性關系[圖6(b)]。這種因變量間的強相關關系表明多維樣本數據本身存在大量冗余信息,也證明采用PCA算法對樣本參數進行降維的必要性。

2.3.2 主成分與抗剪強度關系

根據由βip組成的主成分得分系數矩陣β(表2),將主成分寫成由原始變量組成的線性方程[式(7)]。在將其所得各主成分與樣本抗剪強度參數繪制出的散點圖(圖7)可知,代表土體孔隙特性的第一主成分與黏聚力呈負相關,與代表土體水穩性的第二主成分呈正相關。結果表明,土體孔隙特性越顯著,水穩性越弱,抗剪強度越低。

圖7 主成分與抗剪強度參數散點圖Fig.7 Scatter plot of principal component and shear strength

如將主成分作為解釋變量,直接建立抗剪強度參數主成分回歸模型,即式(8)、式(9);此時,主成分回歸模型對抗剪強度參數的擬合優度分別為Rc=0.54、Rφ=0.69。主成分回歸模型的解釋變量個數大幅降低,但模型擬合精度則有較大提升空間。

Fi=βi1X1+βi2X2+…+βipXp

i=1,2,3;p=1,2,3…

(7)

式(7)中:Fi為樣本對應第i個主成分的主成分綜合得分;Xp為樣本的第p維參數數值。

c=-0.86F1+0.36F2-3.23F3-173.56

(8)

φ=-1.35F1+0.27F2-0.81F3-12.4

(9)

綜上所述,通過主成分分析法可將滆湖組黏性土11個參數,簡化為3個主成分;即保留了大部分原始信息,又避免了多維變量之間多重共線性的影響。第一主成分代表土體孔隙特性,與黏聚力和內摩擦角均呈負相關關系;第二主成分代表土體水穩性,與黏聚力和內摩擦角均呈正相關關系。表明土體孔隙特性越顯著,水穩性越弱,抗剪強度越低。

但僅通過主成分回歸模型建立的隔湖組黏性土抗剪強度參數預測模型精度有提高空間[式(8)、式(9)],可選擇將主成分變量[式(7)]作為神經網絡模型的輸入層,建立抗剪強度參數的PCA-BPNN預測模型。

3 基于PCA-BPNN的抗剪強度預測

3.1 BPNN模型參數

將上述主成分得分矩陣作為輸入層,基于MATLAB軟件,對711組樣本建立PCA-BPNN預測模型,具體步驟如下。

步驟1數據預處理.對711組樣本進行歸一化。訓練集樣本數為421,測試集樣本取145,剩余145組為預測集樣本,可以用于模型驗證。

步驟2輸入層變量數為3,輸出層變量數為2;隱含層數量可以依據式(10)確定。

(10)

式(10)中:h為隱含層數量;m為輸入層數量;n為輸出層數量;a為1～10的可調整常數(為避免過度擬合取3)。

步驟4模型參數結果。

通過對樣本的多次學習訓練,確定隱含層神經元為5時,BPNN預測效果良好。此時,BPNN模型3個主成分為輸入層,其輸入層至隱含層的權值與偏置值,以及隱含層-輸出層權值與偏置值計算結果如表3所示。最終將樣本代入訓練好的模型即可得到預測結果。

表3 BPNN模型的權值和偏置值Table 3 BPNN neural network’s weight and bias values

3.2 預測結果及誤差分析

將711組土工試驗數據劃分為訓練集、測試集與預測集,代入訓練好的模型進行,迭代運算的擬合優度R分別為0.96、0.95、0.96,可見該模型具有較高可靠性,如圖8所示,以主成分分析結果變量作為輸入層,建立PCA-BPNN模型,可以實現對滆湖組黏性土抗剪強度參數的有效預測。

Y為預測模型的預測值圖8 神經網絡模型擬合效果Fig.8 Effect of neural network model prediction set

為驗證PCA-BP模型預測效果,從預測集樣本隨機選取60組樣本進行預測。結果顯示:樣本黏聚力均值c=49.59kPa,模型預測均值c=50.96 kPa,MAE=7.03 kPa,RMSE=8.33 kPa;預測集與真實值相關系數為R=0.94,模型假設檢驗P<0.05;可見預測數據與實際值基本一致,模型對黏聚力的擬合程度較強(圖9)。

圖9 模型對黏聚力的預測效果Fig.9 Effect of cohesion prediction model

而隨機樣本內φ均值為14.9°,模型預測φ均值為14.3°,MAE=0.73°,RMSE=0.92°,R=0.87,模型假設檢驗P≤0.05;對內摩擦角的擬合程度較強,但略低于黏聚力預測模型(圖10)。

圖10 模型對內摩擦角預測效果Fig.10 Effect of internal friction angle prediction model

3.3 預測模型對比分析

為了研究模型預測效果,將總體711組試樣數據代入訓練好的PCA-BPNN模型,將預測結果與主成分回歸模型進行對比。結果顯示:PCA-BPNN模型對抗剪強度參數c、φ預測性能得到在均方誤差等性能方面得到全面提高(表4)。

表4 預測模型性能參數對比Table 4 Comparison of model performance parameters

由此可知,基于PCA-BPNN算法建立的滆湖組抗剪強度預測模型既實現了模型輸入變量的降維,降低了模型計算量,提高了計算效率,又能消除解釋變量之間共線特性,實現多參數土體參數的高精度預測。

4 結論

通過對蘇錫常地區第四系滆湖組711組土黏性土室內試驗樣品數據分析,建立了滆湖組黏性土抗剪強度PCA-BPNN預測模型;得到如下結論。

(1)運用PCA算法可將滆湖組黏性土11維參數變換成3維主成分;第一主成分貢獻率為52.1%第二主成分貢獻率為36.6%;當主成分維度為3時,累計貢獻率達93.5%,三維主成分包含了大部分樣本信息。第一主成分可歸納為土體孔隙特性,與黏聚力和內摩擦角均呈負相關關系;第二主成分可歸納為土體水穩性,與黏聚力和內摩擦角均呈正相關關系;土體孔隙特性越顯著,水穩性越弱,抗剪強度越低。

(2)建立了基于PCA-BPNN算法的滆湖組黏性土抗剪強度反演預測模型。結果顯示:模型預測結果與試驗樣本基本一致,模型的擬合優度R>0.85,隨機樣本c預測均方根誤差<6.84 kPa,φ預測均方根誤差<1.9°;說明該模型可靠性高,能夠對滆湖組黏性土抗剪強度參數進行有效預測。

(3)引入PCA算法建立特殊土參數預測模型,可以避免人工篩選預測變量的不確定因素,不僅能夠實現高維解釋變量降維,又能夠保留樣本大部分信息,從而增加了模型的可靠性。引入PCA算法消除多維變量間多重共線性,避免直接運用神經網絡模型可能引發的過擬合問題;既提升了模型預測精度(均方誤差角度),又能在一定程度上提高預測模型的泛化能力。為運用數學方法研究土體工程地質參數及海量室內土工試驗數據價值的深度挖掘和利用提供了參考。