基于改進對抗解釋結構模型和交叉影響矩陣相乘法的多航站區分區運行設計影響因素分析

李明捷, 王濤, 黃詩軼, 田杰

(中國民用航空飛行學院機場學院, 廣漢 618307)

截至2022年,中國251個民用運輸機場中,有10個機場擁有3座及以上航站樓,38個機場擁有兩座航站樓(包括衛星廳)。較傳統的單體航站樓構成的航站區,多航站區機場在航空器地面運行、地面保障資源分配等方面更加復雜。多航站區分區運行不合理不僅會降低航空旅客的出行體驗,并且還會增加機場運營成本,降低機場整體運行效率。目前中國對多航站區分區運行缺乏統一分區原則,有的機場根據航班性質按國際、國內分配;有的機場根據航空公司及其聯盟分配;有的則依據航路方向、多跑道運行情況等對航空器進行分區停放。

中外學者對多航站區分區運行依據、分區設計以及分區方案運行效率評估等方面的研究十分有限,對多航站區機場的研究主要集中在陸側航站樓和空側機坪方面。趙明明[1]以樞紐機場為研究對象,采用灰色聚類評價法和交通四階段法對多航站區間銜接交通系統進行研究,提出樞紐機場航站區間銜接交通系統優化策略。陳鵬超[2]提出了多航站樓多區域的機位分配問題,從安全性和效益性的角度分別建立了以降低機位運行沖突為目標的多目標機位預分配模型和以降低旅客步行距離、油耗成本、機位空閑成本為目標的多目標機位實時調整模型,并通過實例和仿真軟件進行合理性和可行性驗證。馬俊鵬[3]以樞紐機場的航站樓功能區分區作為研究對象,以提高旅客的服務質量、人員和設施設備的利用效率等為目標,研究了航站樓設計原則和旅客流程等對旅客流的影響,并分析影響旅客容量的環節,最終提出航站樓功能區分區的優化策略。Zhang[4]分析了當下多航站區背景下樞紐機場陸側交通的銜接問題,通過優化機場陸側交通的影響因素和運行模式,提出優先發展公共交通的策略以解決多航站區機場周圍所面臨的交通壓力從而促進機場的發展。相較于傳統單體航站樓車道邊容量評估方法,多航站樓對數據的采集和計算精度都有著更高的要求。基于此,王茹[5]通過時空消耗理論建立了多航站樓車道邊的容量評估模型,并將其應用于天津機場驗證模型的可行性。針對未來樞紐機場多航站樓的發展趨勢,為了實現航站樓的高效分工、提高機場運行效率和旅客服務水平,鄧海超[6]根據中外機場的運行案例,總結分析了影響多航站樓分工的8個因素及邏輯關系。為了對多航站區分區運行進行整體的量化研究,黃詩軼[7]運用決策與實驗室法確定分區原則,借助系統布局規劃理論制定出3種不同的機場多航站區分區運行方案,最后采用Airtop軟件對所設的最優方案進行仿真驗證。

綜上所述,現有的研究大多集中在值機流程中的指派[8]、航站樓容量的利用率[9-10]、機位分配[11]以及機場陸側交通布局[12]等問題,對于多航站樓分區運行方面的研究較少。隨著經濟和民航業的持續穩定發展,越來越多的機場正在被規劃建設或擴建[13]。根據《關于加強民用運輸機場總體規劃工作的指導意見》可知,中國未來會出現更多擁有多個航站樓的大、中型樞紐機場,多航站區協同運行的模式勢在必行。多航站區分區運行對旅客出行的舒適度、航司的運營、機場的資源調度以及運行效率都有著重大的影響,然而目前行業內對于分區運行規劃的原則及方案并未統一,因此,研究機場多航站區的分區運行具有重要意義。

鑒于此,首先通過文獻調研法和德爾菲法識別出多航站區分區運行的影響因素。為克服傳統解釋結構模型(interpretative structural modeling method, ISM)在反映因素間相互作用時較為單一的局限性,提高交叉影響矩陣相乘法(cross-influence matrix multiplication method, MICMAC)在因素驅動力-依賴性分析時的靈敏度[14],引入模糊集理論將因素之間的關聯性模糊化,構建對抗解釋結構模型-模糊交叉影響矩陣相乘法(adversarial interpretive structure modeling method-fuzzy cross-influence matrix multiplication method, AISM-FMICMAC)模型,并通過模糊可達矩陣中截距的分布論證截距取值的合理性。最后,結合對抗層級拓撲圖以及因素的模糊驅動力、模糊依賴性,將復雜繁多的影響因素層次化、清晰化,為多航站區分區運行設計提供理論依據。

1 分區影響因素體系構建

多航站區的分區運行所涉及的內容較多,是一個復雜的系統工程。查閱中外大型樞紐機場的分區運行現狀以及多篇文獻資料之后初步得到分區運行相關的影響因素,然后通過德爾菲法進行影響因素篩選,最終從旅客、機場設計、機場運行、機場設施設備、航空公司5個維度篩選出15個主要影響因素。分區運行影響因素體系如表1所示。

表1 多航站區分區運行設計影響因素體系表Table 1 Multi-terminal Area operational design influence factor system table

2 AISM-FMICMAC模型構建

由上述建立的分區影響因素,邀請多位專家對各因素之間的關聯度進行評分,再根據評分結果進行模型構建,主要建模流程如圖1所示。

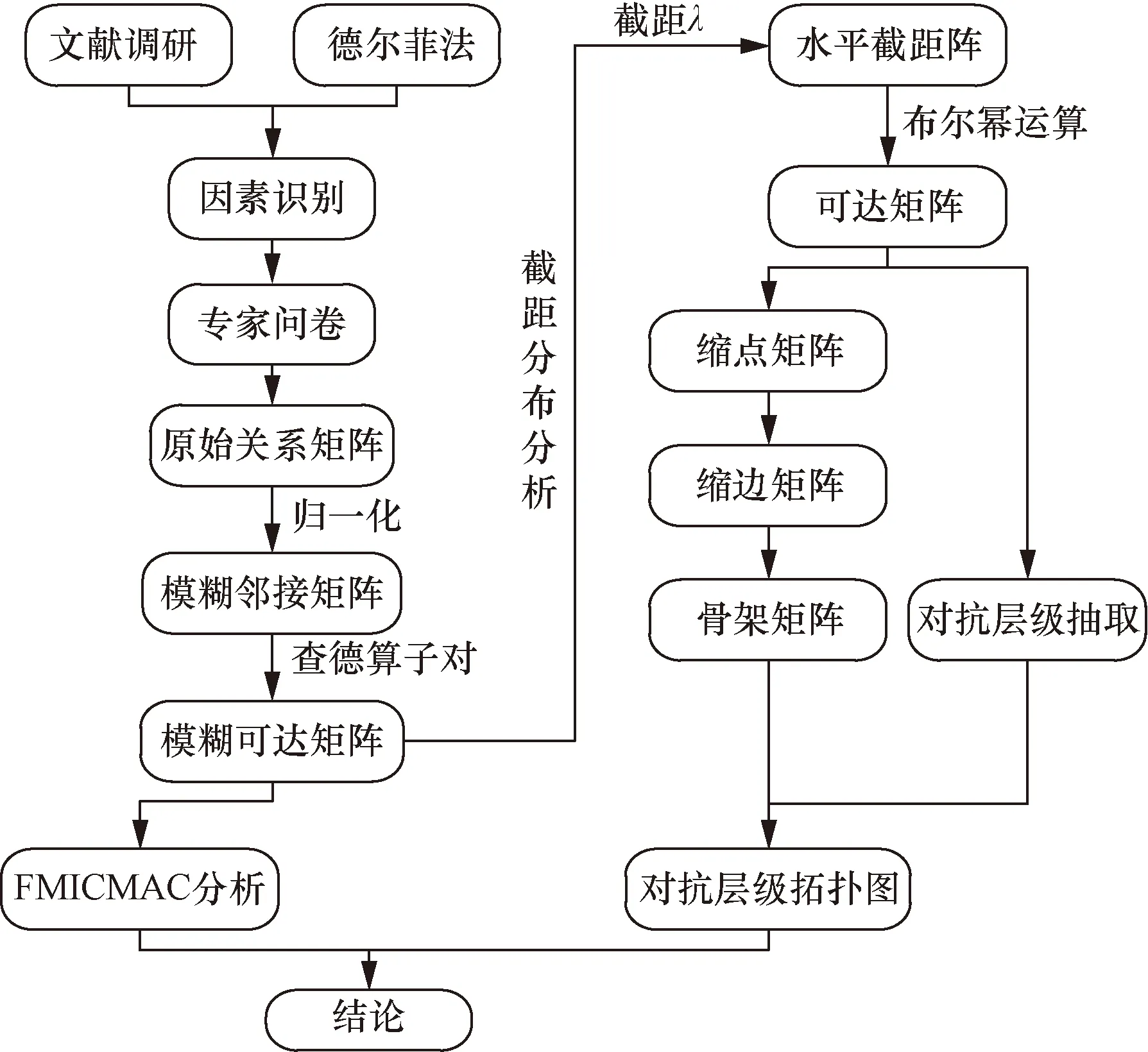
圖1 AISM-FMICMAC建模流程Fig.1 Modeling process of AISM-FMICMAC

2.1 改進的AISM模型構建

解釋結構模型作為結構化模型的一種,是現代系統工程分析中廣泛應用的方法[15]。AISM是在ISM的基礎上加入生成式對抗網絡(generative adversarial networks, GAN)中的博弈對抗(Adversarial)思想,提出的一種新的模型方法。AISM可在保留系統功能完整的情況下,通過相反的層級抽取規則,得出一對最簡的層次化拓撲圖。其對原始數據無特殊要求可兼容多種分析方法,是一種魯棒性較強的決策方法[16]。將模糊數學引入到模型中可一定程度上解決專家評分過程中的不確定性和主觀偏好[17],使得結果更加準確合理。具體的模型構建步驟如下。

2.1.1 原始關系矩陣

設影響因素集合為S,則S={S1,S2,…,Sn}。通過問卷調查和德爾菲法對分區影響因素Si和Sj之間的二元關系進行判斷,得到初始關系矩陣D=(dij)n×n,dij∈(0,10),其中dij為因素之間的原始關聯強度。

2.1.2 模糊鄰接矩陣

(1)

式(1)中:Max(dij)為原始矩陣D中的最大值元素。

2.1.3 模糊可達矩陣

(2)

=(bi1⊙b1j)⊕(bi2⊙b2j)⊕…⊕

(bin⊙bnj)

=(bi1∧b1j)∨

(bi2∧b2j)∨…∨(bin∧bnj)

(3)

(4)

2.1.4 閾值λ和水平截距陣

(5)

2.1.5 可達矩陣

在2.1.4節中經過多次計算,選擇合理的分層劃分閾值λ得到的水平截距陣Rλ,即鄰接矩陣Aλ=(aij)n×n,再通過式(6)求出可達矩陣R=(rij)n×n。

(A+E)1≠(A+E)2≠(A+E)3≠…

≠(A+E)i-1=(A+E)i

=R,i≤n-1

(6)

2.1.6 一般性骨架矩陣

2.1.7 對抗層級拓撲圖

由可達矩陣R,可得到先行集A(Si)、可達集R(Si)、共同集C(Si)。先行集A(Si)為能夠對因素Si產生影響的其他所有因素集合。可達集R(Si)為能夠被因素Si所影響的其他所有因素的集合。共同集為可達集與先行集的交集。

A(Si)={Sj|Sj∈S,Sji=1}

(7)

式(7)中:Sji為第j行第i列元素,Sji=1表示可達矩陣R的每一列Sj中為1的元素。

R(Si)={Si|Si∈S,Sij=1}

(8)

式(8)中:Sij為第i行第j列元素,Sij=1表示可達矩陣R的每一行Si中為1的元素。

C(Si)={Si|Si∈S,A(Si)∩R(Si)}

(9)

(1)UP型層級拓撲圖。即通過結果優先的層級劃分抽取方式,抽取規則為:C(Si)=R(Si)。可達集與共同集相同時,所抽取的元素放在上層,抽取的放置順序是從上往下[18]。

(2)DOWN型層級拓撲圖。即通過原因優先的層級劃分抽取方式,抽取規則:C(Si)=A(Si)。先行集與共同集相同時,所抽取的元素放在下層,抽取的放置順序是從下往上[18]。

2.2 水平截距分布

(10)

式(10)中:zλ為模糊可達矩陣中截距為λ的數量;n為模糊可達矩陣的階數。

2.3 基于FMICMAC的分區影響因素分析

采用Fuzzy-MICMAC方法確定影響因素的模糊依賴性Qi與模糊驅動力Hi,同時分析因素在體系中所處的位置及其作用。

(11)

(12)

3 實例分析

實例分析以粵港澳大灣區某干線機場的遠期規劃為例。該機場遠期總體規劃可滿足旅客終端年航班起降54×104架次,旅客吞吐量8 000萬人次,其中國內旅客占比70%,國際旅客占比30%。該機場現有兩條跑道、3座航站樓(東航站樓、T3航站樓、S1衛星廳),并規劃新建第3條跑道以及T4航站樓。以該機場為例,在T3航站樓、T4航站樓、東航站樓、衛星廳共同運行的背景下,即4個航站樓3個航站區的模式下,運用AISM-FMICMAC模型進行機場多航站區分區運行設計影響因素研究。

3.1 AISM-FMICMAC應用

表2 模糊可達矩陣Table 2 Fuzzy reachability matrix

合理的取值能夠反映出影響因素之間真實的關聯性[21],由模糊可達矩陣可得閾值集合為{0.28,0.33,0.39,0.44,0.5,0.56,0.61,0.67,0.72,0.78,0.830.89,0.94,1},經過多次迭代計算后可知:當λ=0.67時,模型能夠給呈現出較好的解釋結果。并由式(5)得出閾值為0.67的截距陣R0.67,再通過式(6)可計算出表3中的可達矩陣R。

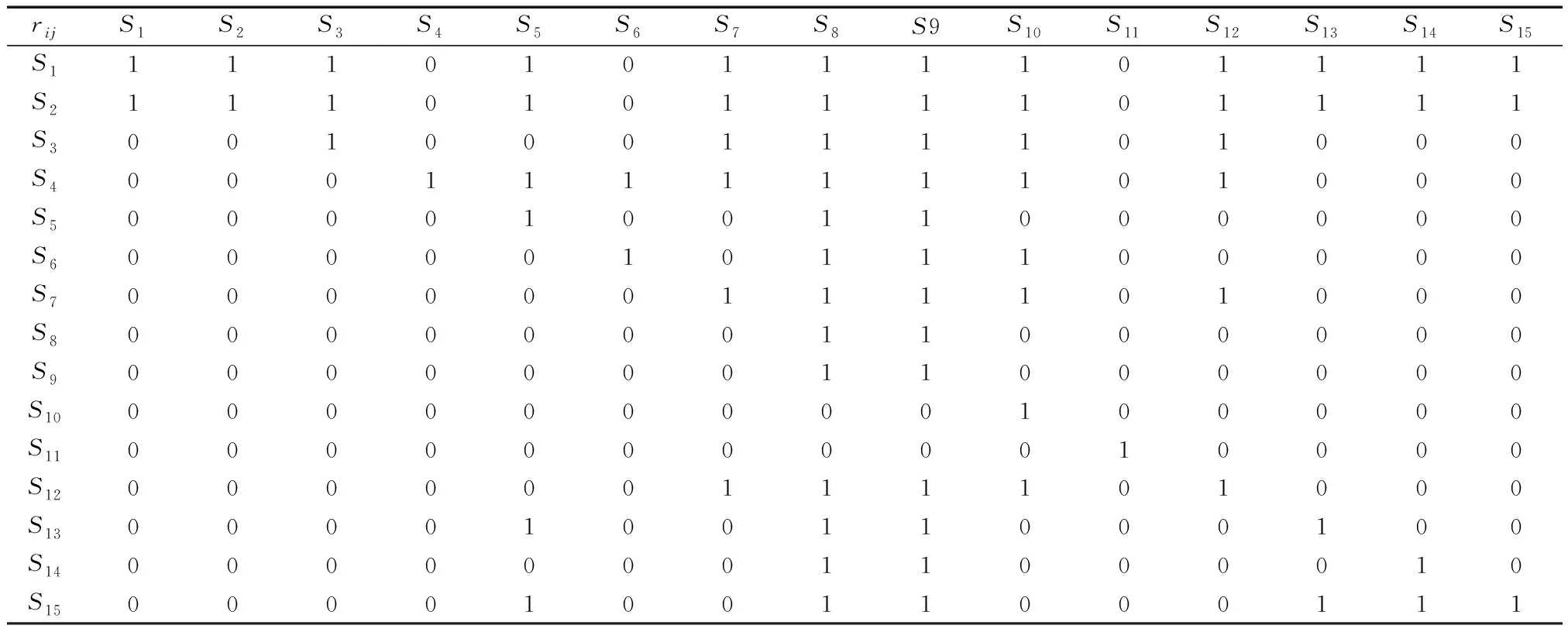
表3 可達矩陣Table 3 Reachability matrix

藍色區域中的要素為活動要素;L1～L5表示各因素所處的不同層級圖2 對抗層級拓撲圖Fig.2 Confrontation hierarchy topology diagram

圖3 FMICMAC分析Fig.3 FMICMAC analysis

表4 一般性骨架矩陣Table 4 General skeleton matrix

表5 對抗層級抽取結果Table 5 Confrontation hierarchy division results

3.2 水平截距分布分析及可達矩陣的建立

3.2.1 水平截距分布分析

由上述已求出的截距,通過式(10)可求出各截距的占比并繪制直方圖,如圖4所示。可以看出,截距為0.28時占比24%;截距為0.5時占比18%;截距為0.56時占比11%;截距為0.61時和0.67占比相同均為14%;截距為0.72時占比最小,截距最小值為0.28,最大值為0.94。根據表2中模糊可達矩陣中的值可知,截距區間為[0.28,1],但圖4中沒有將截距為1時考慮入內,即模糊可達矩陣的對角線值,根據自反性原理,式(10)中截距總數為n(n-1)而非n×n。

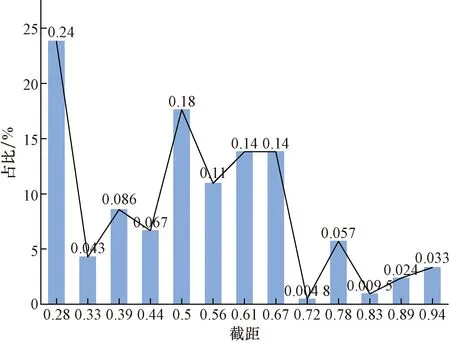
圖4 截距分布Fig.4 Distribution of intercept distance

選擇截距進行模糊可達矩陣至布爾矩陣的轉換時,這一過程會選擇那些影響值較為顯著的,即高于截距的值而舍去較低值,最后將所得的布爾矩陣作為AISM的輸入。因此合理截距選擇對模型分析結果至關重要。

最契合模型結果的截距并不一定是所有截距中占比最高的那個。如圖4所示,0.28和0.5這兩個截距的占比都遠高于其他截距,但經過計算后可知兩者在最終的層級分層效果較差,沒有達到顯著性的區分效果。截距0.56、0.61、0.67的占比雖不及0.28和0.5,可以看出,其趨勢逐漸上升且趨于平穩。通過計算比較發現三者中截距取0.67時,模型能夠得到較好的解釋結果,經過多次的測算后發現截距的取值一般處于截距區間中段,截距較大或較小都會導致后續的AISM要素層級劃分過于堆積。

3.2.2 可達矩陣建立

上述兩種不同的求解方式在相同截距下所得出的可達矩陣結構一致,但兩者的求解效率卻有很大區別。模糊可達矩陣的截距陣數量是小于等于模糊矩陣的截距陣數量,并且模糊可達矩陣的截距陣自身便是可達矩陣。選擇第一種方式的意義在于模糊可達矩陣。通過模糊可達矩陣既可以進行FMICMAC分析,提高傳統MICMAC分析的靈敏度,同時可以更快地進行截距分布分析,對截距選取的合理性進行預先判定,最終結合計算結果給出最優截距值。

3.3 AISM影響因素層次結構分析

如圖2中的UP型(左側)和DOWN型(右側)層級拓撲圖所示,藍色區域因素S11(航站樓內旅客服務設施的完備性)為孤立因素。S11既沒有指出方向的有向線段也沒有指進的有向線段,即該因素在整個系統中較為獨立,與其他因素不產生交互影響。從FMICMAC分析(圖3)也可知,S11的依賴性和驅動力都較低、影響也較小。

存在活動要素的拓撲系統為可變拓撲系統或者拓撲活動系統,不存在活動要素的系統為拓撲剛性系統。圖2中藍色區域中的要素為活動要素,故整個系統為可變拓撲系統。活動要素處在對抗層級拓撲圖中不同的層級并可進行層級躍遷。

整個系統中存在3個回路,即S1和S2、S7和S12、S8和S9,這些因素之間具有強關聯可以作為一個要素或一個整體。在實際的分區運行設計時可將回路縮減為單個整體進行考慮從而提高分析的準確率和效率。

整個系統因素分為5個層級和3個發展進程。由影響因素對抗層級抽取規則,形成從上到下L1～L5形式的因素重要度階梯分布。有向線段指向表示可達,即原因到結果。不考慮孤立因素的因果層級系列如表6所示。由于是可變拓撲系統,故UP型和DOWN型的因果系列并不相同。3個發展進程是指孤立因素去除之后將因素層級劃分為:上層、中層、下層。

表6 因果層級Table 6 Cause and effect hierarchy

下層因素呈現出很強的原因屬性,對其他因素產生影響,在拓撲圖中只發出有向線段。因此對圖中的下層因素求并集可得到根本層因素{S1,S2}∪{S4,S1,S2}={S1,S2,S4},即整個系統的根本因素為S1、S2、S4。這些因素可直接或間接的影響系統內的其他因素,對于多航站區的分區運行來說,這些因素對分區之后的運行效率起著主導作用,在分區時應該重點關注。

上層因素即結果層因素,處在系統的最高層。不發出有向線段僅受其他因素影響,對上層因素求并集可得結果層因素{S8,S9}∪{S8,S9,S10}={S8,S9,S10},此3個因素是影響分區運行效率的最直接的因素,系統中其他因素的影響都需要通過上層因素得到實現,具有很強的結果屬性。

中間層因素也可稱為過渡層因素。它們既受下層因素的影響同時又將影響傳遞給結果層因素。本系統內的中間層要素分布在L2～L4層級內,這8個過渡層因素是影響分區運行效率的核心因素,因此在設計時需要優先考慮以保證整個系統的穩定性。

3.4 FMICMAC分析

由圖3中的分區影響因素FMICMAC分析可知,15個影響因素分為如下三類。

(1)處在Ⅱ類的自治因素。此類因素有S3(各航空公司中轉和國際旅客占比)、S4(機坪布局形式)、S6(機場滑行道布局的合理性)、S11(航站樓內旅客服務設施的完備性)、S13(基地航空公司飛機數量在該機場占比情況)。Ⅱ類因素在整個系統中有著承上啟下的作用,與底層和深層因素之間關聯度較低。S13和S4的驅動力值較高但依賴性值相對較低,即該類因素對其他因素有較大影響而受其他因素影響較小,故此類因素在分區中應該優先考慮以提升整個體系的穩定性。

(2)處于Ⅰ類的獨立因素,包括S1(各航空公司年旅客吞吐量)、S2(各航空公司高峰小時旅客數量)、S14(廉價航空公司飛機數量在該機場占比情況)、S15(各航空公司飛機機型及其比例)。此類因素具有較高的驅動力和較低的依賴性,在整個系統里較少依賴其他因素而對其他因素都有著間接或直接的影響,對航站區的分區來說是作為關鍵和根本的因素,尤其是航司的年旅客吞吐量以及高峰小時旅客數量需要重點把握。

(3)從FMICMAC分析圖(圖3)中可以看出,沒有依賴性和驅動力都強的影響因素存在。

(4)處于Ⅲ類的依賴因素,包括S5(機位類型與數量)、S7(機場勤務道路的通達性)、S8(跑道運行模式)、S9(機位分配與使用策略)、S10(機場地面保障資源調度系統的效率)、S12(分散式航站樓間捷運系統通達性),此類因素驅動力較低而依賴性較高,因素間的關聯較為復雜且容易受到其他因素的影響。依賴因素大多處于系統的上層,對底層和過渡層因素的依賴性較高,但此類因素對分區運行效率的影響十分顯著,如S11航站樓內旅客服務設施的完備性對于S12航站樓間捷運系統通達性有著明顯的提升進而影響旅客值機進程和航站樓內的運行效率。

3.5 多航站區分區運行的策略分析

(1)對進行多航站區的分區設計時應該重點考慮被劃分進相應區域航空公司的年旅客吞吐量和高峰小時旅客數量。作為影響分區的根本因素,在機場的運行和效益等方面都占據重要位置。一些大型的樞紐機場會設置專門化的航站區,能夠進行客源的集中,并吸引旅客數較多的航空公司入駐,可以為機場帶來的更多收益的同時也面向旅客提供差異化的需求。

(2)大型的樞紐機場其中轉旅客占據很大比例。因此,對于此類的機場航站區分區需要注意的是機坪的布局,若機位也隨著航站樓的分區而進行分區管理,這對于航班的日常保障以及旅客的乘機來說也帶來了便利性,所以應該加強機位和和航站樓之間的協調性以滿足不同中轉旅客和國際旅客的便利性需求。

(3)為了保障分區之后運行的穩定性,應該完善航站樓內的旅客服務設施,簡化航站樓內旅客的登機流程。同時應該提高不同航站樓之間捷運系統的通達性以便旅客的中轉和換乘。對于那些較大跨越性的航站樓單體或多元結構設計,必須完善航站樓間的功能設施,建設空側捷運系統,同時加強行李系統的跨區中轉及保障等功能。

4 結論

鑒于當下中外大型樞紐機場的多航站樓、多機坪運行現狀及發展規劃,構建AISM-FMICMAC模型對影響多航站區分區運行的各因素進行分析,得出如下結論。

(1)基于文獻調研和德爾菲法綜合分析得到機場多航站區分區運行設計的影響15個因素,具體涵蓋旅客、航空公司、機場設施設備、機場設計以及機場運行5個方面。

(2)運用模糊集理論對AISM-FMICMAC方法進行改進,克服專家評估過程中的主觀性以及個人偏好同時提高MICMAC分析時的靈敏度。由模糊可達矩陣兩種不同的求解路徑和截距分布得出截距分布圖,驗證其對于截距取值的合理性。

(3)運用AISM-FMICMAC方法將多航站區分區的影響因素分別劃分為獨立因素、聯系因素、自治因素、依賴因素四類,并對其進行量化和分層,直觀展示出不同層級因素對分區運行規劃的影響。直接層影響因素為跑道運行模式和機位分配與使用策略,深層次影響因素為航空公司的年旅客吞吐量和高峰小時旅客數。

(4)根據AISM和FMICMAC分析提出相應的分區運行策略,為機場的多航站區分區運行設計提供理論支撐。