基于哈密頓力學的斜交網格筒-核心筒結構協同分析

胡啟平, 宋佳樂

(河北工程大學土木工程學院, 邯鄲 056038)

斜交網格結構作為一種特殊的新型建筑結構,其獨特的結構形式受到越來越多的關注,應用也越來越廣泛,比較著名的建筑有廣州西塔、阿聯酋首都門以及深圳建成的京基100等[1-4]。

高層斜交網格結構有斜交網格筒和斜交網格筒-核心筒等結構形式[1]。21世紀以來,中外學者逐漸加強了對斜交網格筒-核心筒結構的理論研究。Moon等[2]首先提出了斜交網格筒中斜柱截面初步設計的方法,并推導了結構的抗側剛度公式,其主要思路是考慮結構中腹板的抗側能力,忽略翼緣側對抗側剛度的影響,將斜交網格筒體等效為懸臂梁。滕軍等[5]采用彈塑性動力時程分析法,以鋼管混凝土斜交網格筒-鋼筋混凝土核心筒結構為例,研究結構體系中構件的屈服順序及內外筒抗震協同受力性能。史慶軒等[6]從結構的塑性發展過程、受力情況、變形能力、內外筒的抗側剛度及剪力滯后等方面,對斜交網格筒-鋼筋混凝土核心筒結構協同工作的受力性能進行了系統的分析。劉成清等[7-8]、方登甲等[9]通過斜交網格筒的抗側剛度、內外筒結構的內力分布、結構的倒塌機制及延性等因素探討結構的抗震性能,并建立相同參數的框架-剪力墻結構模型進行對比分析。張鋒等[10]采用等效連續化方法將斜交網格筒等效為各向異性連續筒體,基于能量變分原理推導結構的位移場閉合解。通過進一步分析得到結構的內力和變形特征,結果表明,該類結構的變形是彎曲型和剪切型的疊加,且具有明顯的剪力滯后效應。胡啟平等將框筒結構、筒中筒結構等簡化為具有彎曲變形和剪切變形的懸臂梁,通過哈密頓力學對結構的協同工作性能、二階效應及動力特性進行分析,并采用精細積分法對方程進行數值求解,避免了復雜的公式推導且計算精度高[11-17]。

擬研究的斜交網格筒-核心筒結構是由斜交網格筒與開有洞口的鋼筋混凝土核心筒組成的新型筒中筒結構體系,其中斜交網格筒主要通過斜柱的軸向拉壓來承受豎向荷載和側向荷載,相比于傳統結構體系,該結構體系抗側承載力高、受力情況復雜。作為一種新型結構體系,其受力特性和簡化計算方法仍需深入研究。為了對斜交網格筒-核心筒結構協同工作性能進行研究,往往需對該結構進行簡化處理。采用連續化方法,考慮外筒的剪力滯后效應[18-19]以及內外筒的彎曲變形和剪切變形,將斜交網格筒等效為正交各向異性連續筒體,將開有洞口的鋼筋混凝土剪力墻核心筒簡化為雙肢剪力墻模型。

采用哈密頓力學的方法,根據勒讓德變換引入對偶變量,推導協同分析的哈密頓正則方程,結合精細積分法求解結構的側移和內力分布。將本文方法與有限元方法進行對比,以驗證本文方法的正確性,通過進一步分析得出斜柱不同參數變化對斜柱軸力及內外筒結構協同工作性能的影響。該方法給斜交網格筒-核心筒結構的力學求解提供了一種新思路、新方法,為工程初步設計及后續理論研究提供參考。

1 結構簡化計算模型

斜交網格筒-核心筒結構是由斜交網格筒與核心筒兩種類型的抗側力單元組成,內外筒結構在梁板的約束和協調作用下共同抵抗側向荷載。等效連續化方法是高層建筑結構簡化計算常用的分析方法,采用連續化方法將斜交網格筒等效為連續筒體,將開有洞口的鋼筋混凝土剪力墻核心筒簡化為雙肢剪力墻模型,同時考慮內外筒的彎曲變形和剪切變形,將連接內外筒的樓板等效為剛性連桿。基于以上方法,該結構協同分析的空間模型可簡化為平面模型,計算簡圖如圖1所示,簡化分析采用如下基本假定:①樓板自身平面內剛度無限大,平面外剛度忽略不計,內外筒通過剛性樓板連接,樓板的作用沿高度連續化,兩者水平變形協調一致;②考慮斜交網格筒與核心筒的彎曲變形和剪切變形,將其等效為兩根均勻連續的鐵摩辛柯懸臂梁;③不考慮結構的扭轉效應;④斜交網格筒與核心筒各層剛度保持不變。在實際工程應用中,當各層剛度變化不大時,宜采用加權平均值。

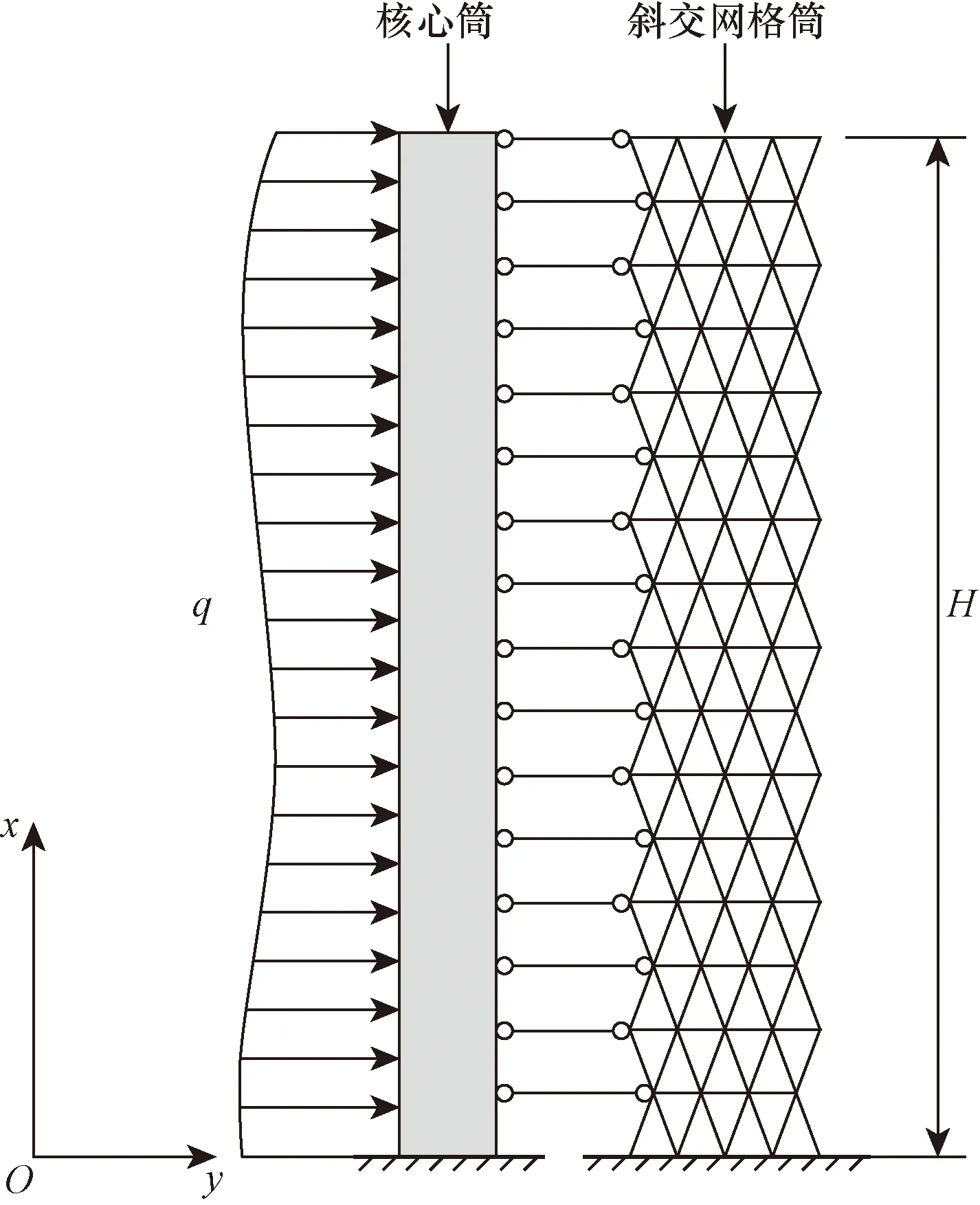
q為外荷載;H為結構樓層高度圖1 高層斜交網格筒-核心筒結構計算簡圖Fig.1 Sketch for calculation of high-rise diagonal intersecting grid cylinder-core cylinder structure

采用文獻[10]中的連續化方法將斜交網格筒中斜柱和環梁組成的穩定三角形單元等效為均勻的正交異性板,形成一個由若干正交異性板圍成的實腹薄壁筒體,如圖2所示。等效連續化模型計算的關鍵是求出等效筒體的等效彈性模量和等效剪切模量。采用連續板單元與斜交網格單元的豎向剛度和剪切剛度相等原則,推導等效連續體的等效彈性模量Eequ與等效剪切模量Gequ,其表達式分別為

(1)

(2)

(3)

式中:Ed、Ad分別為斜交網格筒中斜柱的彈性模量和截面面積;b和t分別為連續板殼單元的寬度和厚度;α為斜柱與水平面的夾角;l為斜柱間距。

內筒采用開有洞口的鋼筋混凝土核心筒,其中洞口將核心筒劃分為4片各自獨立的“L”型剪力墻,通過連梁將它們連在一起。參考高層建筑中剪力墻的分類[20],可按照雙肢剪力墻模型計算。為簡化分析,采用文獻[21]中雙肢剪力墻等效抗彎剛度E2I2和等效抗剪剛度G2A2的計算方法,其中,E2為核心筒的彈性模量,I2為核心筒的慣性矩,G2為核心筒的剪切模量,A2為核心筒的橫截面面積,具體推導過程可參閱文獻。

2 位移場函數及拉格朗日函數

選取等效連續筒體的側移v1(z)、截面轉角θ1(z)、翼緣和腹板的最大縱向位移差函數W1(z)和W2(z)作為廣義位移,考慮斜交網格筒的剪力滯后效應,假設結構中翼緣與腹板的縱向位移場函數分別為二次曲線和三次曲線,構造等效筒體翼緣和腹板的縱向位移場函數為

(4)

式(4)中:wf為等效連續筒的翼緣側Z方向位移場;z、y為坐標;ww為腹板側Z方向位移場;a為翼緣側寬度的1/2;b為腹板側寬度的1/2。

等效連續筒體的應變能可表示為

(5)

式(5)中:Ef、Gf分別為翼緣等效彈性模量和等效剪切模量;εzf為翼緣側正應變;A為積分區域面積;γxz為翼緣側剪切應變;Ew、Gw為腹板等效彈性模量和等效剪切模量;εzw為腹板側正應變;γyz為腹板側剪切應變;A1為斜交網格筒的積分區域。

將核心筒簡化為雙肢剪力墻,不考慮剪力滯后效應。選取核心筒的側移v2(z)、截面轉角θ2(z)作為廣義位移,剪力墻的縱向位移符合平截面假定,位移場為

w=-yθ2(z)

(6)

核心筒的應變能為

(7)

式(7)中:A2為核心筒的積分區域;E2為核心筒的彈性模量;εz為核心筒的正應變;G2為核心筒的剪切模量;γz為核心筒的剪切應變。

由于剛性樓板的作用,內外筒兩個抗側力體系水平變形協調,即v(z)=v1(z)=v2(z)。

當結構上作用沿高度變化的側向荷載q(z)時,結構的外力勢能為

(8)

結構的總勢能為

Π=Π1+Π2+Π3

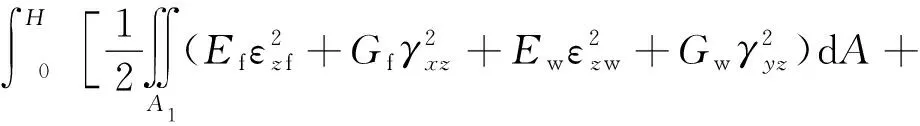
(9)

結構的總勢能密度表達式即為斜交網格筒-核心筒結構協同分析的拉格朗日函數為

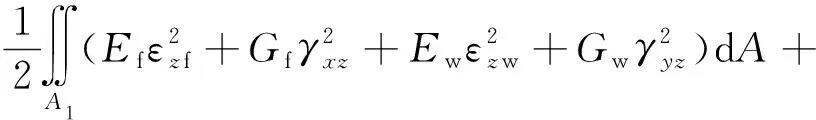
(10)

式(10)中的應變分量可由位移場函數和彈性力學的幾何方程求出,整理后拉格朗日函數的矩陣表達式為

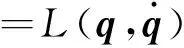
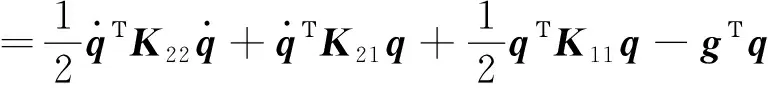
(11)

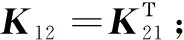
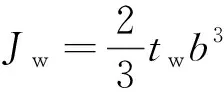
3 哈密頓對偶體系

通過勒讓德變換,引入廣義位移q的對偶變量p,p的物理意義即為廣義位移對應的廣義力。其表達式為

(12)

將問題由拉格朗日力學體系轉變到哈密頓力學體系,導出哈密頓函數為

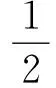
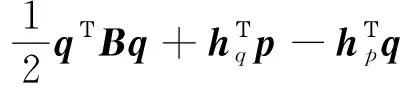
(13)

由式(13),得到哈密頓正則方程[22]為

(14)

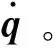
4 結構內力計算

通過對實腹筒體斷面應變積分,求出斜柱相交節點位置的內力,再利用相交節點的平衡關系可以得到斜柱的軸力。翼緣側平面相交節點的豎向力Nz與水平力Qz可分別表示為

(15)

式(15)中:xj為翼緣側相交斜柱的平面節點位置;lf為翼緣側相交斜柱柱距。

腹板側平面相交節點的豎向力與水平力為

(16)

式(16)中:yj為腹板側相交斜柱的平面節點位置;lw為腹板側相交斜柱柱距。

利用式(15)和式(16),結合節點平衡條件,求出高度z處的斜柱軸力為

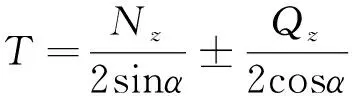
(17)

5 計算實例

某外筒采用斜交網格筒,內筒采用開洞的鋼筋混凝土核心筒的筒中筒高層建筑結構共54層,層高為3.9 m,總高度為210.6 m。外筒平面尺寸為36 m×36 m,斜柱柱距為9 m,與水平面夾角α=69°,截面為箱形,尺寸為800 mm(寬)×800 mm(高)×20 mm(壁厚)×20 mm(壁厚),環梁截面也為箱形,尺寸為300 mm(寬)×800 mm(高)×20 mm(壁厚)×20 mm(壁厚),外筒材料彈性模量Ed為206 GPa。內筒平面尺寸為18 mm×18 mm,墻肢寬度為8 m,連梁高度為1 m,墻肢厚度為0.4 m,混凝土采用C60;結構承受頂點集中荷載101.4 kN。

按2～4節的方法算出簡化計算模型對應的各個物理量后,即可確定式(14)。利用MATLAB編程采用精細積分算法可以快速計算出廣義位移和廣義力,進而得到協同分析所需的結構側向位移及各項內力。

為了驗證本文方法的正確性,采用ETABS軟件對高層結構進行了有限元分析。在有限元程序中,采用剛架單元模擬斜柱和環梁,墻單元模擬核心筒剪力墻。兩種方法計算結果對比如圖3～圖6所示。兩種方法計算結果除少數數據外,相對誤差都小于5%。

圖3 結構側向位移Fig.3 Lateral displacement of structure

由圖3的側移可以發現,斜交網格筒-核心筒結構的側向變形為“彎曲型”。

斜交網格筒-核心筒結構樓層彎矩分布如圖4所示,內外筒的樓層最大彎矩均作用在基底處,且隨著樓層的增加而減小,外筒各樓層彎矩明顯大于內筒,因此外筒承擔更多的彎矩,為結構的主要抗彎構件。結構樓層剪力分布如圖5所示,有限元方法分析得到的內外筒樓層剪力存在起伏變化。而由于本文方法采用連續化假定,無法反映實際受力狀態下樓層剪力的突變,因此內外筒剪力沒有起伏變化,計算得到的結構剪力近似為定值。結構中內筒的最大剪力作用在基底處,隨著樓層的增加而減小,外筒的剪力隨樓層的增加而增大,除底部少數樓層外,外筒承擔更多的剪力,為結構主要的抗剪構件。

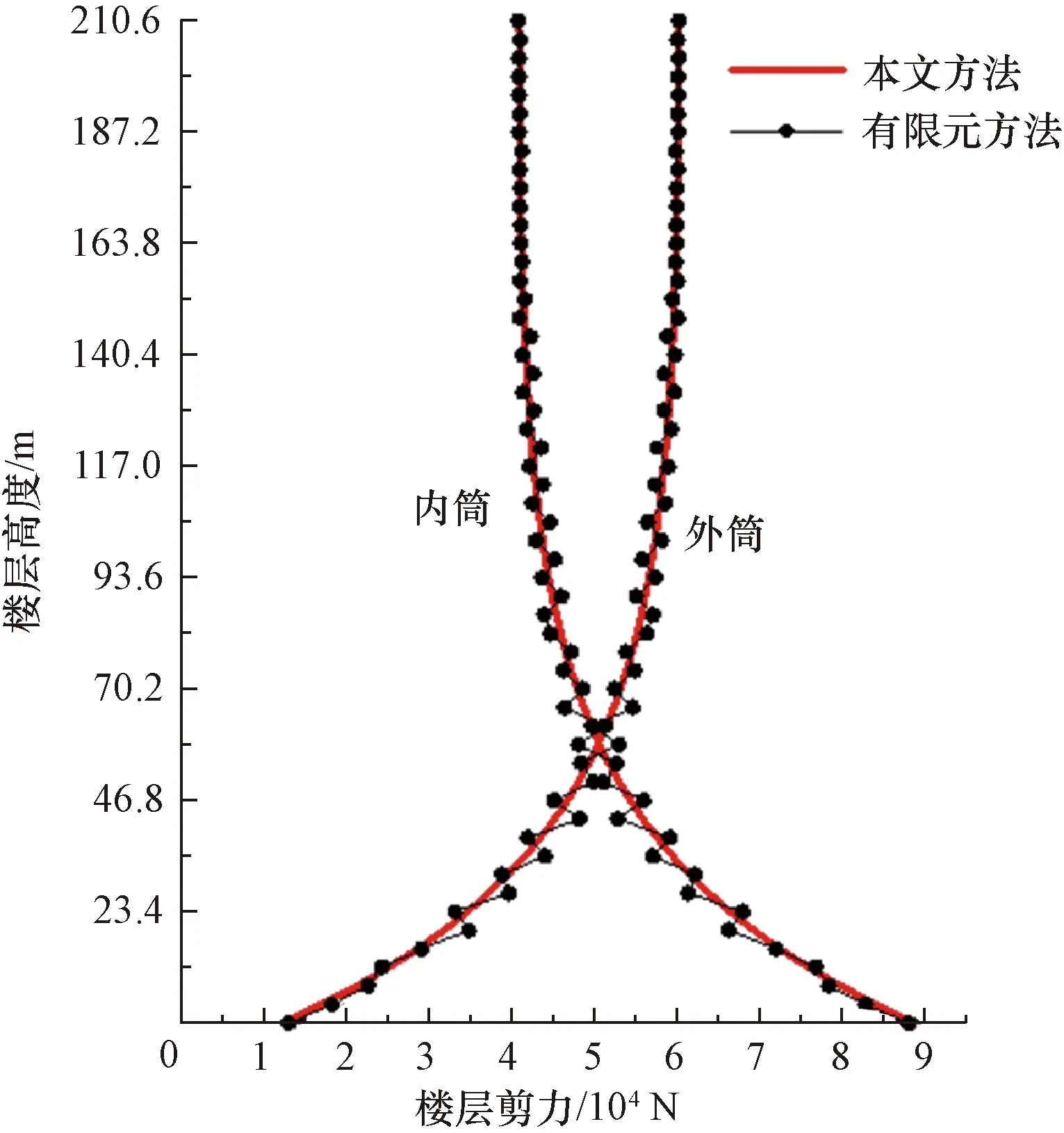
圖5 結構樓層剪力分布Fig.5 Shear force distribution of structural floors

標高z=11.7 m處節點力與斜柱軸力分布如圖6所示。可以看出,本文方法與有限元計算結果吻合良好。在側向荷載作用下,結構中的斜柱主要承受軸力作用,腹板側存在受壓區與受拉區,兩區域相互重疊,導致內力圖中腹板側斜柱軸力存在起伏變化。翼緣側斜柱內力是由腹板側斜柱內力通過角部相交斜柱傳遞而來,內力的傳遞途徑在轉角處發生轉折,傳遞而來的軸力交叉分配到翼緣側的斜柱上。基于相交節點豎向力對斜交網格筒-核心筒結構剪力滯后效應進行研究,整個分析過程簡便,更能體現結構的整體內力分布。從圖6中可以看出,斜交網格筒-核心筒結構具有明顯的剪力滯后效應。

圖6 頂點集中荷載作用下內力結果對比Fig.6 Comparison of internal force results under concentrated load at the vertex

本文方法得到斜柱區段標高處的剪力和彎矩如表1所示。

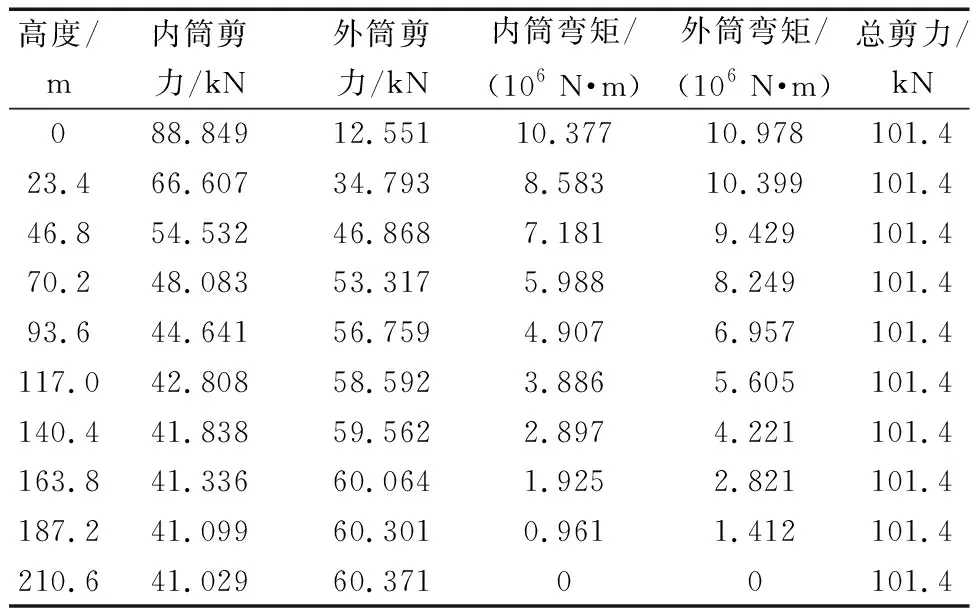
表1 結構的剪力和彎矩Table 1 Structural shear force and bending moment

6 協同工作影響因素分析

斜交網格筒-核心筒結構作為一種新型的雙重抗側力結構,其受力機理與傳統結構不同,斜交網格筒-核心筒結構具有較強的彎曲剛度和剪切剛度。通過理論研究發現,斜交網格筒和核心筒的彎曲剛度與剪切剛度對結構的側向位移及內力影響較為明顯。外筒剛度的控制因素為斜柱角度和斜柱的截面尺寸,本節通過改變斜柱截面尺寸來研究斜交網格筒-核心筒結構協同工作性能的影響。

對上述算例模型中斜交網格筒的斜柱截面進行調整,截面由原始的800 mm(寬)×800 mm(高)×20 mm(壁厚)×20 mm(壁厚)改變為1 000 mm(寬)×1 000 mm(高)×40 mm(壁厚)×40 mm(壁厚)和600 mm(寬)×600 mm(高)×20 mm(壁厚)×20 mm(壁厚),分析結果如表2所示。

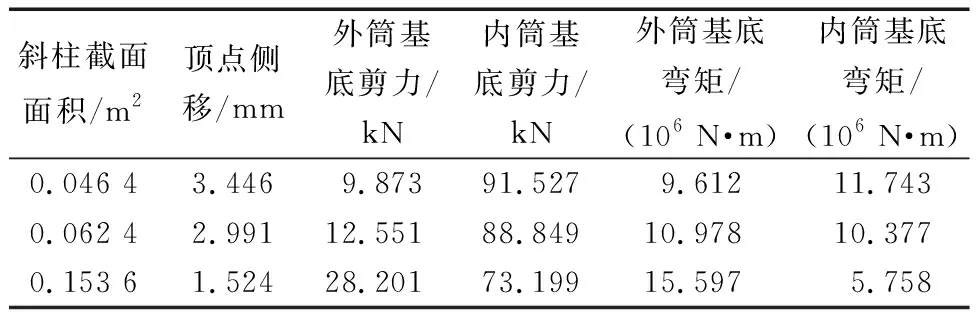
表2 不同斜柱截面下結構的側移和內力Table 2 Side displacement and internal force of the structure under different inclined column sections

從表2數據中可以看出,當斜柱截面面積減小25%時,結構的頂點側移增大13%。隨著斜柱截面面積的減小,斜交網格筒的剛度逐漸減小,結構的整體彎曲側移和剪切側移增大。當斜柱截面面積較小時,基底的彎矩和剪力主要由核心筒承擔。相反地,當斜柱截面面積增大59%時,結構的頂點側移減小49%。隨著斜柱截面面積的增加,斜交網格筒承擔的彎矩和剪力逐漸增大,成為結構中主要的抗彎構件和抗剪構件。研究表明,斜柱截面面積對斜交網格筒-核心筒結構的協同工作性能有顯著影響。

7 結論

(1)哈密頓力學提出斜交網格筒-核心筒結構協同分析新方法,并采用精細積分法求解出高精度數值解,理論推導過程便捷。與有限元方法對比,數值吻合良好,一般相對誤差不超過5%,驗證了本文方法的正確性。該方法可在結構初步設計階段對結構方案進行快速分析驗證。

(2)斜交網格筒-核心筒結構在水平荷載作用下的側向變形呈“彎曲型”。區別于一般的框架-核心筒結構,斜交網格筒-核心筒大部分的樓層剪力和彎矩由斜交網格筒承擔。除底部少數樓層外,其余樓層剪力沿高度變化不大。

(3)斜交網格筒-核心筒結構具有明顯的剪力滯后效應,本文方法能夠較準確地分析剪力滯后效應的影響。

(4)分析了斜交網格筒-核心筒結構的斜柱截面面積對內外筒結構協同工作的影響。結果表明,當斜柱的截面面積增大,側移將明顯減小,斜交網格筒承擔的彎矩和剪力增大,成為結構的主要抗彎構件和抗剪構件。