基于量綱分析的戈壁地區爆破振動衰減模型

李賀龍, 王浩, 諸洲, 張建經, 郭建婷, 牛家永

(1.中核華辰建筑工程有限公司, 西安 712000; 2.中鐵北京工程局集團有限公司工管中心, 北京 102308; 3.西南交通大學土木工程學院, 成都 610031; 4.寧夏水利科學研究院, 銀川 750021)

隨著中國經濟建設的蓬勃發展和爆破技術的不斷進步,工程爆破廣泛應用于礦山、水利水電、交通、建筑等領域[1],成為一種不可或缺的工程施工手段。它在帶來巨大社會經濟效益的同時,工程爆破也給周圍的人員、設備、建(構)筑物以及環境帶來了不可忽略的負面效應[2]。爆破振動的破壞作用是工程爆破負面效應中最重要的問題之一[3],已引起中外研究者和工程技術人員的廣泛關注[4-5]。

薩道夫斯基公式在中外應用廣泛,中國的《爆破安全規程》(GB6722—2014)也采用這一公式計算相應的物理量。由于影響爆破振動傳播和衰減規律的因素十分復雜,對于不同地區的爆破工程,其地質特征和爆破參數差異較大,且中國大部分衰減模型參數更適用于爆破工程開展次數較多的南方地區[6]。對于戈壁地區的重要工程,由于在歷史上開展的爆破施工相對較少,無相關數據可供參考,因此需要根據項目所在地的地質和地形條件建立該地區的衰減模型,為爆破方案設計提供指導。工程實踐表明,平整地形條件下的薩道夫斯基公式預測質點爆破振動速度精度較高,而在地形地貌變化較大的爆破工程場地,薩道夫斯基公式預測精度則較低[7]。僅考慮裝藥量和爆心距兩個因素得到的計算公式往往精度不高,所以很多學者在特定工程條件下對薩道夫斯基公式進行修正[8]。大范圍的巖石場地基坑開挖需要進行多次爆破施工,這將導致爆破場地的地形地貌發生較大變化,加之戈壁地區具有特殊的地質條件,因此需要建立具有區域特征的爆破振動速度預測公式[9]。但是,目前尚無可綜合考慮戈壁地區地質、地形等影響因素的爆破振動公式。

目前中外計算爆破振動速度時普遍采用爆破振動速度的大小與比例藥量(Q1/3/R,其中,Q為一次起爆總藥量,R為測點至爆源的距離)的α次方(α為衰減指數)成正比的薩道夫斯基公式。然而薩道夫斯基公式的建立是基于球形藥包洞室爆破的大量實測數據經統計分析得到,該公式對球形藥包引起的爆破振動速度預測比較準確[10]。目前柱狀藥包廣泛應用于中外大型爆破工程中,它和常用的球形藥包相比具有爆堆集中、地震效應小、拋擲距離遠、爆破方量多、破碎度更均勻等優點[11]。對于柱狀藥包而言,不同裝藥方式對爆破振動有很大的影響[12],利用球形藥包爆破所推導出的公式計算柱狀藥包誘發的爆破振動速度,顯然存在較大的缺陷。深孔柱狀裝藥的起爆方式通常為逐排起爆,成排炮孔的分散藥包爆炸誘發的地震波與單一藥包不同,如果簡單地將分散藥包假設為集中藥包進行爆破振動速度計算,將會產生明顯的誤差。當爆破施工現場周圍有重要的構筑物時,由于構筑物與爆破場地的距離較近,逐排起爆時爆破地震波具有明顯的疊加效應,按照集中藥包進行計算將低估爆破振動速度[13]。

現以寧夏危險廢棄物處理中心建設項目的基坑爆破開挖為工程背景,基于大量的現場監測數據建立戈壁地區的爆破振動速度衰減模型。為了提高模型精度,通過考慮裝藥特征對爆破振動的影響,基于量綱分析理論推導出成排深孔爆破振動速度預測公式,并與實測結果進行對比分析,以驗證所提出爆破振動公式的準確性。研究成果可應用于戈壁地區露天深孔爆破工程的設計與振動控制。

1 工程概況現場監測結果分析

1.1 工程概況

寧夏危險廢棄物處理中心建設項目位于寧夏石嘴山市北部的戈壁地區,根據工程現場的實際情況及設計要求,選取垂直高度上一次性大斷面爆破和分層爆破兩種施工方案。由項目所在區域的地形地質條件、周圍環境、施工工期、施工要求以及周邊子項對爆破振動的要求,首先應對一期M-1、M-3、M-5、M-7、M-9和M-10子項周邊9 m范圍內的石方進行機械破碎(無法滿足爆破振動對主體結構的影響),再實施A、B、C區域的爆破施工,區域分層爆破如圖1所示。

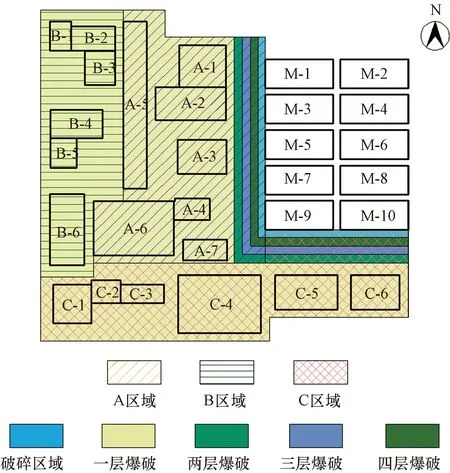
圖1 區域分層爆破示意圖Fig.1 Schematic diagram of regional layered blasting

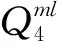
1.2 基坑爆破監測

本次爆破振動監測獲取了大量的振動測試數據,為了保證監測結果的統一性,選取爆破區域地形條件相似,起爆聯網方式相同、爆破參數及藥量大致相同、外部因素影響較小的7次爆破振動監測進行分析,對信號進行預處理后,共獲取22組有效監測數據。選取其中一次典型爆破監測方案為例進行說明,C-4段基坑采用一次性大斷面爆破,起爆方式為從南到北逐排起爆,爆破孔網參數具體為:①炮孔采用垂直孔,炮孔直徑為90 mm,炮孔深度為14 m;②炮孔超深深度為1.1 m,即測點與基坑底部的高程差為12.9 m;③垂直平行孔的密集系數為1.2;④最小抵抗線為2 m;⑤炮孔孔距為3 m,炮孔排距為2.5 m;⑥填塞長度為2.7 m;⑦炸藥單耗為0.35 kg/m3,炮孔單孔裝藥量為36.7 kg;⑧炮孔內選用秒發雷管,同一排炮孔之間選用即發雷管,排間選用接力雷管Ms5(110 ms);炮孔和監測點具體位置如圖2所示。

圖2 爆破炮孔及測點布置圖Fig.2 Layout of blasting holes and measuring points

1.3 爆破振動速度衰減規律

中國爆破工程大多根據現場實測數據對薩道夫斯基公式中的未知參量K和α進行回歸分析,得到爆破振動速度衰減規律。式(1)為中國現行《爆破安全規程》(GB 6722—2014)[14]中采用的薩道夫斯基公式。

(1)

式(1)中:V為質點振動速度幅值;Q為一次起爆總藥量;R為測點至爆源的距離;K和α分別為與爆破現場地形、地質條件有關的特征系數和衰減指數。

根據現場實測數據回歸得到薩道夫斯基公式中的系數K和衰減指數α,水平徑向、水平切向和垂直向的爆破振動速度衰減公式如表1所示。圖3為水平徑向和垂直向振動速度的回歸曲線。可以看出水平徑向、垂直向的振動速度V與比例距離R/Q1/3呈指數衰減關系。當R/Q1/3的值小于4時,振動速度衰減較快,當R/Q1/3的值大于4時,振動速度衰減趨勢減弱,且逐漸趨于平緩。水平徑向振動速度整體略大于垂直向振動速度,由于爆破振動測試場地為逐排深孔爆破,炮孔中的柱狀藥包爆炸激起平行于地面方向傳播的柱面波,所布置的測點距爆區較近,柱面波特征比較明顯,在柱狀波陣面作用下,水平徑向振動速度整體上略大于垂直向振動速度。

表1 爆破振動速度衰減公式Table 1 Attenuation formula of blasting vibration velocity

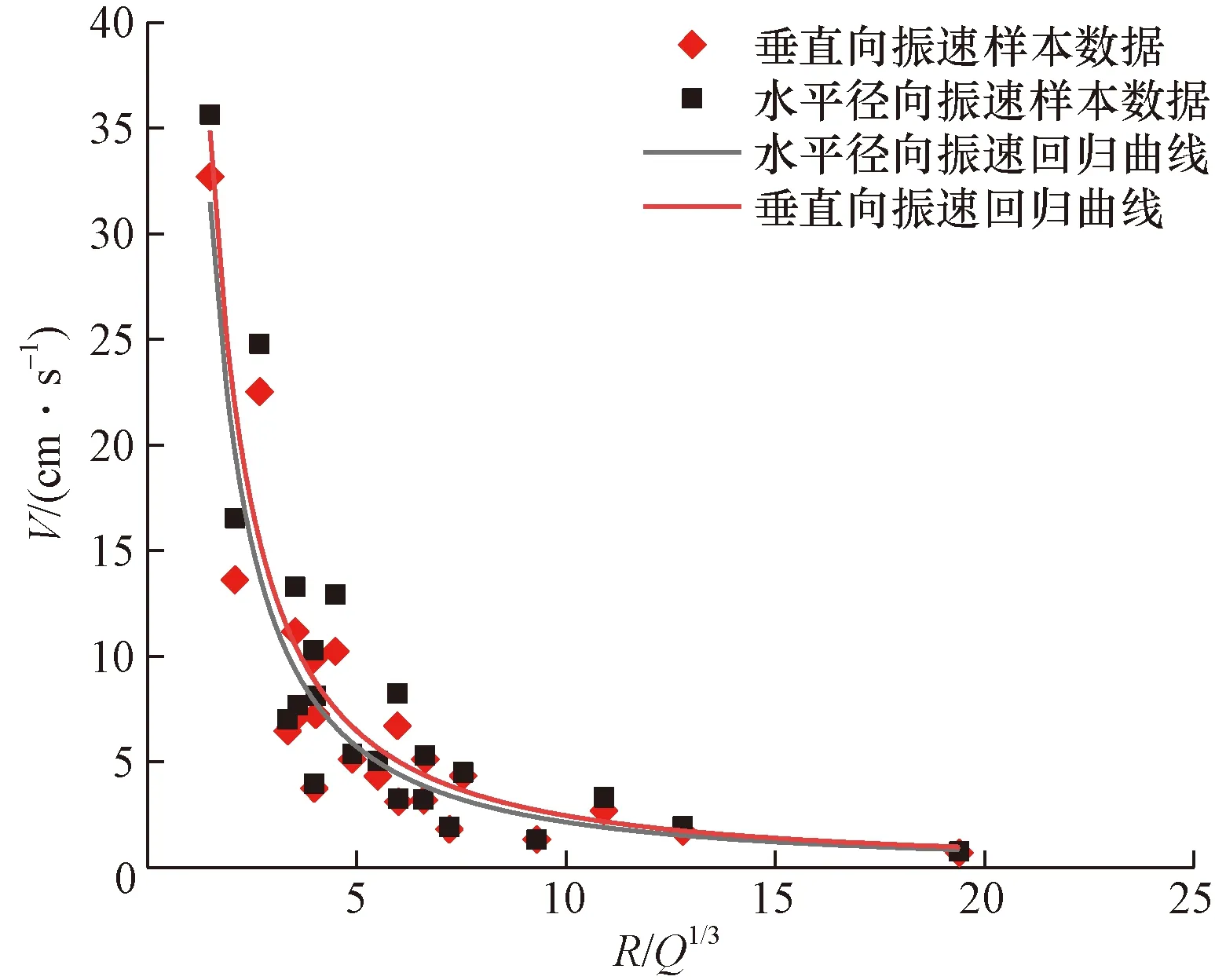
圖3 水平徑向和垂直向的振動速度回歸曲線Fig.3 Horizontal radial and vertical vibration velocity regression curves

2 爆破振動速度的量綱分析

2.1 公式推導

爆破地震波引起地面振動是一個復雜的過程,受很多因素影響,如裝藥量、裝藥類型、裝藥結構、爆源與測點間的距離、地形與地質、巖土性質等[15-17]。按照幾何參數、巖石參數、炸藥參數進行分類,根據基坑爆破開挖現場的地形地貌和起爆網絡,以計算結果與實測結果盡可能接近為目標,選取影響爆破振動速度的因素,如表2所示。

表2 爆破振動速度衰減規律的影響因素Table 2 Influencing factors of blasting vibration velocity attenuation law

從表2可以看出,表征爆破振動速度的參數很多,完全考慮所有參數會導致量綱分析得到的無量綱變量函數異常復雜。根據基坑爆破開挖現場的地形地貌和爆破條件,推導平整場地條件下,逐排深孔爆破引起的質點振動速度計算公式,所以,此處選取藥包半徑(rB)、測點到成排炮孔幾何中心的直線距離(R)、單排炮孔連線長度(S)、炸藥密度(ρB)、爆轟波速度(DB)、巖體密度(ρR)、巖體聲波速度(CR)和巖體彈性模量(ER)8個主要影響因素作為自變量,運用量綱分析理論構建爆破振動速度V的預測公式。成排深孔爆破幾何示意圖如圖4所示。

圖4 成排深孔爆破幾何示意圖Fig.4 Geometric diagram of row deep hole blasting

在量綱分析中,爆破振動速度與多個物理量具有函數關系,可表示為

V=Φ(rB,R,S,ρB,DB,ρR,CR,ER)

(2)

所分析問題的物理量參數n=9,取炸藥密度(ρB),爆轟波速度(DB)測點到成排炮孔的垂直距離(R)為獨立量綱,獨立量綱數m=3,因此可以用n-m=7個無量綱數組πi(i=1,2,…,6)來表示上述物理量參數。根據π定理可得

(3)

式(3)中:α、β、γ為待定系數。

因為π是無量綱量,所以式(2)中分子分母的量綱相等,由ρB、D、R與rB的量綱可得

dimrB=L=(ML-3)α(LT-1)β(L)γ

(4)

式(4)中:對于L有γ=1;對于T有α=β=0。

則有

(5)

同理可得

(6)

將式(5)和式(6)代入式(2)可得

(7)

實際工程中,對于同一爆破場地,其炸藥種類、裝藥密度和巖體特性變化不大,可以將炸藥密度(ρB)、巖體密度ρR、巖體聲波速度(CR)、爆轟波速度(DB)和巖體彈性模量(ER)近似看為常數。因此,式(7)可簡寫為

(8)

不同無量綱數π的乘積和乘方仍為無量綱數,令:

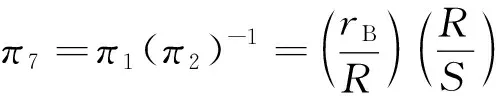
(9)

(10)

對于球形藥包,其藥包半徑在炸藥密度不變的情況下可以表示為藥量的立方根,即rB≌Q1/3。因此,球形藥包成排孔同時起爆的振動速度預測公式可寫為

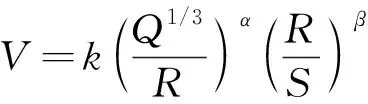
(11)

式(11)中:V為峰值質點振動速度,m/s;k為與爆源至測點間的地形、地質條件有關的影響系數;Q為一次起爆總藥量,kg;R為測點至爆源的距離,m;α為柱狀藥包比例距離影響系數;S為單排炮孔連線長度,m;β為成排炮孔同時起爆影響系數。

當測點與爆源的距離很遠時,成排孔中各藥包到測點的距離很接近,若此時將分散藥包當作集中藥包計算,式(11)可寫為

(12)

式(12)即為當前中國廣泛使用的薩道夫斯基公式。

對于柱狀藥包,其藥包半徑在裝藥密度不變的情況下可以表示為藥量的平方根,即rB≌Q1/2,由式(10)可知,柱狀藥包成排孔同時起爆的振動速度預測公式可寫為

(13)

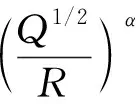
2.2 公式回歸擬合

將式(13)兩端取對數,使其線性化,可得

(14)

lnk=c,a=α,b=β,則式(14)可表示為

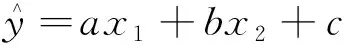
(15)

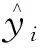
(16)

利用數學分析中的極值原理,求使偏差平方和δ取最小值時所對應的系數a、b、c的值。若使式(16)偏差平方和最小,則其必要條件為

(17)

即

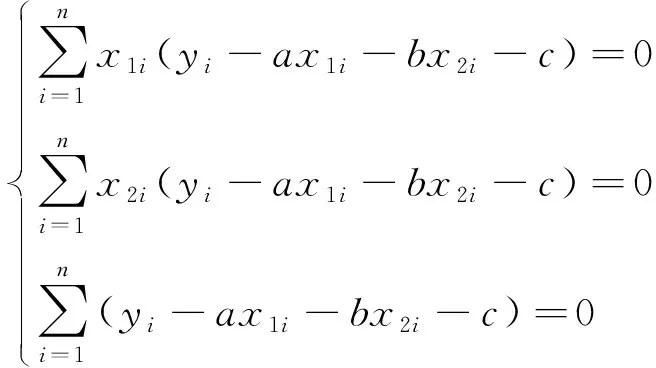
(18)

整理式(18)得

(19)

式(19)中:n為第n個實測值。

將現場實測數據代入式(19)中的三元一次方程組即可求得回歸方程[式(15)]中的系數a、b、c的值,進而求得式(13)中k、α、β的值,得到成排深孔爆破振動速度預測公式。

2.3 預測結果對比分析

所推導的逐排深孔爆破振動速度計算公式建立了爆破振動速度與其主要影響因素之間的數學關系,通過和傳統的薩道夫斯基爆破振動速度預測公式對比預測精度,驗證本文公式的準確性和有效性。采用計算值與實測值之間的相對誤差來衡量爆破振動速度預測公式計算值的預測精度,相對誤差按式(20)計算。

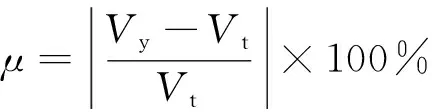
(20)

式(20)中:Vy為預測振動速度;Vt為實測振動速度。

利用現場實測數據回歸得到式(13)水平徑向、水平切向和垂直方向上的爆破振動速度預測公式分別為

(21)

(22)

(23)

式中:Vra、Vta、Vve分別為水平徑向、水平切向和垂直方向上的爆破振動速度。

所推導的爆破振動速度預測公式與傳統薩道夫斯基公式在水平徑向、水平切向、垂直向上計算結果的相對計算誤差分別如表3～表5所示。

表3 水平徑向爆破振動速度計算公式相對誤差Table 3 Relative error of calculation formula for vibration velocity of horizontal radial blasting

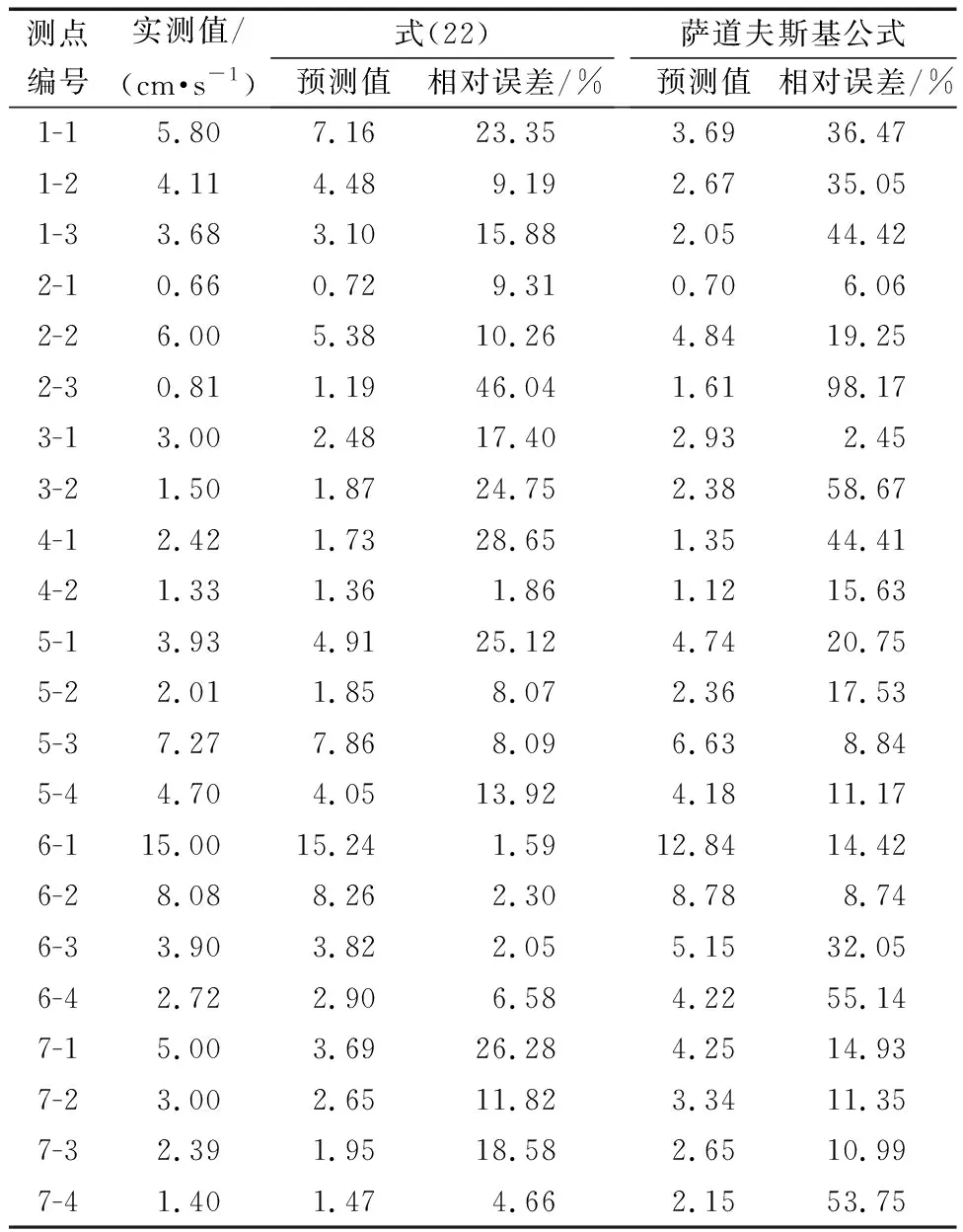
表4 水平切向爆破振動速度計算公式相對誤差Table 4 Relative error of calculation formula for vibration velocity of horizontal tangential blasting

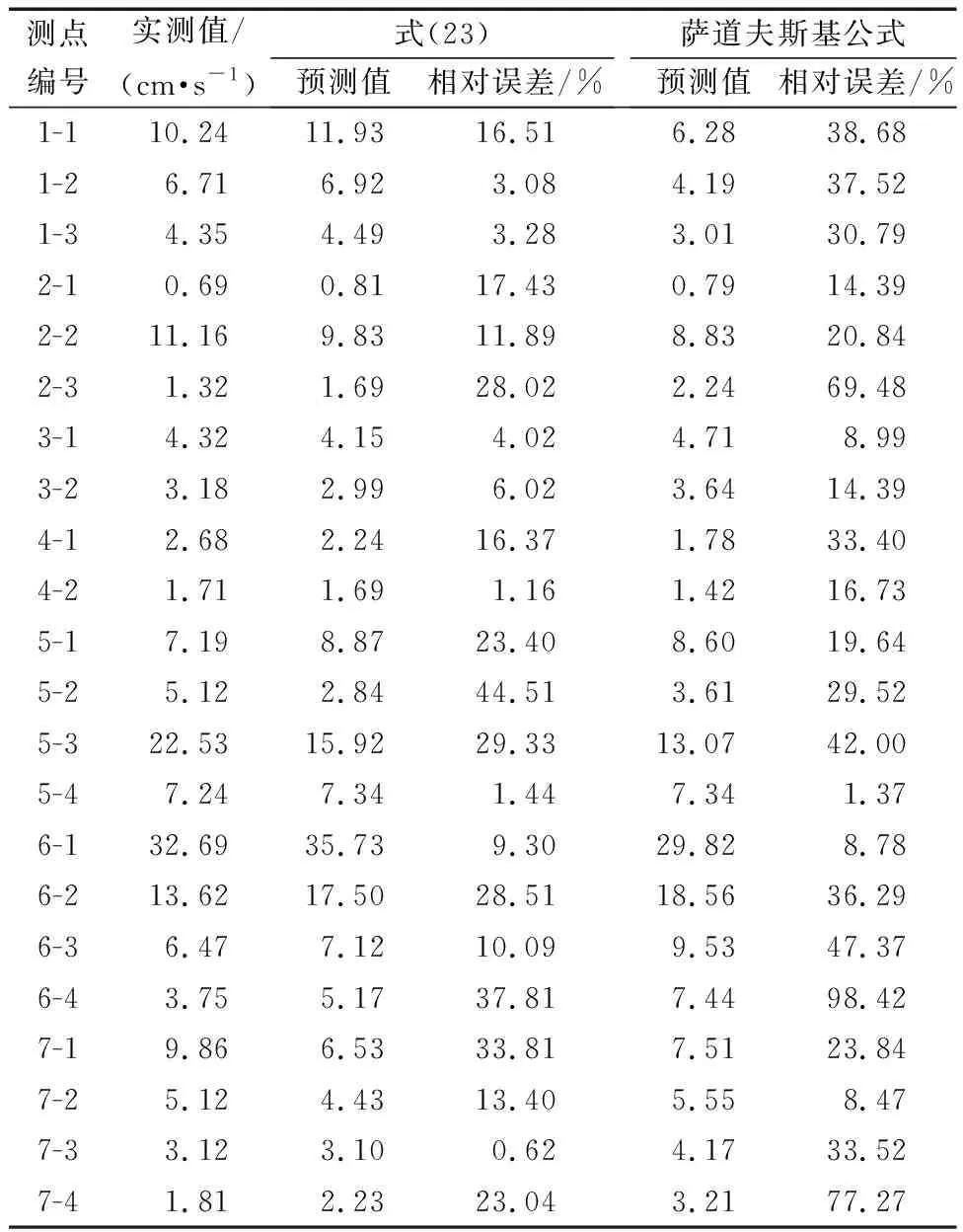
表5 垂直向爆破振動速度計算公式相對誤差Table 5 Relative error of calculation formula for vibration velocity of vertical blasting

由表3～表5可知,所推導的爆破振動速度預測公式計算得到的水平徑向、水平切向和垂直向爆破振動速度平均相對誤差分別為17.36%、14.35%、16.50%,而薩道夫斯基公式預測得到的水平徑向、水平切向和垂直向爆破振動速度平均相對誤差分別為34.95%、28.19%、32.35%。可知成排深孔爆破條件下用本文推導的公式預測爆破振動速度誤差較小,采用薩道夫斯基公式預測誤差較大,薩道夫斯基公式預測值的平均相對誤差約為本文推導爆破振動速度預測公式的2倍。因此,本文推導得到的爆破振動速度預測公式能較準確地反映平整場地條件下成排深孔爆破振動速度的衰減規律。

3 結論

(2)將推導得到爆破振動速度預測公式與薩道夫斯基公式進行現場應用對比分析,結果發現新推導公式的水平徑向、水平切向和垂直向振動速度預測精度均高于薩氏公式,薩道夫斯基公式預測值的平均相對誤差約為新推導公式的兩倍。說明推導得到的爆破振動速度預測公式能較準確地反映平整場地條件下成排深孔爆破振動速度的衰減規律。