數形結合：讓小學數學教學提質增效

摘 要：數形結合是重要的數學思想，是學生數學學習提質增效的助力。學生可以借助“形”認知“數”，借助“數”掌握“形”，從而掌握數學學習方法，鍛煉數學學習能力。基于此，小學數學教師有必要將數形結合思想融入數學教學，實現以形助數，以數輔形。基于此，文章分兩部分論述數形結合思想在小學數學教學中的運用策略，第一部分重在論述數形結合思想的滲透價值，第二部分重在介紹數形結合思想的滲透策略。

關鍵詞：小學數學；數形結合思想；滲透策略

中圖分類號：G427? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? 文獻標識碼：A? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?文章編號：2097-1737（2023）23-0031-03

數形結合思想是數學學科的基本思想方法，是以數和形關系為基礎，借助數和形的相互轉化來解決問題的思想方法[1]。眾所周知，數學的研究對象是數與形。小學數學四大領域均建立在數與形的基礎上。在形的輔助下，學生可以認知數；在數的助力下，學生可以理解形。

然而，在傳統的數學教學中，部分教師忽視數學學科特點，機械地灌輸數學知識點，忽視數形結合思想的滲透，導致大部分學生知其然不知其所以然，影響了學習興趣、學習質量，甚至承受了過重的課業負擔、心理壓力。針對此情況，小學數學教師有必要滲透數形結合思想。

一、滲透數形結合思想的必要性

（一）數形結合思想的教育價值

1.提高學生的思維能力

在成長的過程中，個體的認知結構也在不斷重組、改造。依據個體的認知發展特點，皮亞杰將認知發展分為四個階段。小學生的認知發展處于具體運算階段和形式運算階段。在這兩個階段，小學生的形象思維較發達，往往依賴實物、直觀形象來建立認知。在實物、直觀形象的助力下，他們獲得邏輯運算、推理機會，有利于發展邏輯思維能力。數形結合思想能借助直觀的形（實物、圖像、線段、圖形等）展現抽象的事物，使學生發揮形象思維作用，克服種種認知障礙，建立良好的數學認知[2]。

2.優化學生的認知結構

建構認知結構其實是聯系新舊知識的過程。無論何種認知結構，都可以用符號、圖像、動作進行表征，但對大部分小學生來說，數學邏輯性強、抽象程度高，很難理解。教師滲透數形結合思想能夠借助直觀的圖像、線段等，展現不同知識點之間的聯系，助力學生建構數學認知[3]。

3.增強學生的問題解決能力

解決數學問題是數學學科的重要活動，也是學生學習數學的目的之一。數形結合思想作為“數”與“形”相互轉化的手段，可以使學生借助具體的形象表征來分析、解決復雜的數學問題[4]。例如，在解決數學應用題時，學生可以把握關鍵信息，繪制線段圖、示意圖等，直觀地展現數量關系，把握問題本質，理清問題解決思路，繼而列式、運算，解決問題。長此以往，學生會扎實掌握問題解決方法，積累問題解決經驗，提升問題解決能力。

4.培養學生的審美情趣

從數學研究歷史上看，在很長的一段時間內，

“數”與“形”處于割裂狀態。在解析幾何創立之后，

“數”與“形”實現結合。二者的結合展現了數學的簡潔美、統一美、和諧美等，如可以用直觀的“形”展現抽象復雜的“數”（文字、數、方程等）。學生在長期學習和應用數形結合思想的過程中，不僅可以建構深刻的數學認知，還可以在不知不覺中受到數學多元美的熏陶，有利于培養良好的審美情趣。

（二）新課標要求

《義務教育數學課程標準（2022年版）》（以下簡稱《課程標準》）是數學教學的導向。《課程標準》強調了數學學科的抽象性，提出直觀化教學要求。在教學中，教師要引導學生從生活現象中抽象出數學知識，從具體事物中抽象出簡單的幾何體和平面圖形。同時，《課程標準》在過去“雙基”的基礎上增加了數學基本思想、基本的數學活動經驗。這些要求均強調了數形結合思想的重要性。

綜上所述，教師在小學數學教學中滲透數形結合思想，能在降低數學學習難度的基礎上，讓學生在知識、方法、能力等方面有所發展，實現數學教學提質增效。所以，小學數學教師應采用適宜的策略滲透數形結合思想。

二、滲透數形結合思想的策略

（一）以形助數

1.以形助數，掌握數學概念

數學概念是數學學科的基礎內容，具有概括性、抽象性[5]。在學習數學概念時，學生要分析、對比大量實例，發現其統一屬性。形是學生進行對比的助力。教師可以依據具體的數學概念，呈現相關的形，引導學生觀察、對比，歸納統一屬性，認知數學概念。

例如，在“千以內數的認識”這節課上，學生要了解計數單位之間的關系。對此，教師可以操作電子白板，先后展示一個小立方體、十個小立方體、一百個小立方體、一千個小立方體，而學生認真觀察小立方體從一到千的數量變化過程。在此過程中，教師可以引導學生對比不同的模型，讓學生分析它們之間的關系。在對比時，很多學生會發揮形象思維作用，發現“十個1是10，十個10是100，十個100是1000”。基于此，學生會在腦海中建立“十進制”的概念。教師可以趁機介紹計數單位之間的十進制關系，使學生建構清晰的認知。這樣學習數學概念更高效。在這一過程中，學生可以在腦海中建立深刻的直觀表象，提高記憶水平，同時汲取學習經驗，學會借助形學習數。

2.以形助數，化解學習難點

“數形結合”不僅是一種數學思想，而且是一種切實可行的數學學習方法。在學習數學時，學生受到思維能力、認知水平等因素的影響，會遇到諸多學習難點，如數學概念、復雜的數學運算等。教師可以發揮數形結合思想的作用，引導學生刻畫形，展現數學現象，并進行觀察、分析、歸納，逐步得出數學結論，輕松化解學習難點。

例如，在教學“異分母分數加減法”時，教師可以先呈現情境圖，引導學生觀察、思考、列式。基于學生的列式結果，教師可以鼓勵他們對比所學，發現不同之處。在已有認知的支撐下，學生很容易發現所列出的算式是異分母分數加法。教師可以趁機引導學生思索異分母分數加法的計算方法。

在學生沒有解題思路的情況下，教師可以鼓勵他們拿出一張長方形紙，將它對折，為其中二分之一的部分涂色。在學生涂色后，教師可以引導他們繼續對折這張紙，為其中四分之一的部分涂色。面對操作成果，學生認真觀察，很容易發現“兩次涂色的部分一共占了這張紙的四分之三”。一些認知水平較高的學生會發散思維，發現“二分之一是兩個四分之一”，“二分之一加四分之一是四分之三”。教師可以引導學生分析此過程和結果。在分析時，學生不斷觀察涂色情況，

回想自己的發現，確定“在進行異分母分數加法計算時，需要將兩個分數的分母化成同一個數”。這時，教師可以引出“通分”這一概念。與此同時，教師可以操作電子白板，演示類似現象。學生通過不斷觀察、思考，得出結論——在進行異分母分數加法計算時，要先通分，再進行同分母分數加法計算。如此學習使學生輕松掌握了算理，提高了數學運算水平。

3.以形助數，解決數學問題

善于解決數學問題不是指善于遵循一定的標準來解決問題，而是能獨立思考，使用恰當的方法解決問題[6]。數形結合是學生解決數學問題的助手，學生通過繪制線段圖，可以直觀地發現問題中的數量關系，順利解決問題。又如，學生通過繪制圖像、圖表等，可以直觀地發現數學問題中蘊含的規律，找到解決問題的方法。對此，小學數學教師可以引導學生借助形來解決數學問題。

例如，在學習“倍的認識”時，學生要解決應用題：“超市的一盒軍棋8元，一盒象棋是軍棋價格的

4倍。請問，一盒象棋多少錢？”在剛剛認知“倍”的概念的情況下，大部分學生面對這個應用題很容易摸不著頭腦。這時，教師可以指導他們繪制線段圖。教師可以引導學生將8元看作一個線段。學生會遷移課堂認知，畫出4段同樣長的線段，展現“一盒象棋是軍棋價格的4倍”的含義。在直觀、清晰的線段圖的作用下，學生發散思維，轉化數學問題，如“求象棋的價格，就是在求4盒軍棋的價格”。如此一來，學生可以輕松列出算式：8×4，得出結果：32。教師可以依據學生的問題解決情況，總結解題方法——畫線段圖，強化認知。同時，教師可以呈現其他類似問題，鼓勵學生自主解決。在解決問題后，大部分學生利用線段圖展現問題中的條件，獲取數量關系并列式、計算。學生體驗這樣的數學問題解決活動，切實掌握了方法，建構了以形助數的認知，有利于今后解決數學問題。

（二）以數輔形

1.以數輔形，感知圖形特點

盡管幾何圖形的性質具有直觀性，但是在缺乏量化分析的情況下，學生對圖形的特征是難以判斷的。對此，小學數學教師應引導學生借助數來分析形，把握數量關系，確定圖形的特點，增強對圖形的認知。

例如，在教學“長方形和正方形”時，教師可以為學生提供大小不同的長方形模型，引導學生觀察、測量，建立表格，展現每個長方形模型的長、寬、角等信息。在操作的過程中，學生獲得數據，建立表格，認真對比，發現長方形的特點，如，“長方形的四個角都是直角”“長方形的對邊相等”“長方形永遠有兩個長邊和兩個短邊”等。基于學生的發現，教師可以進行歸納，使學生建立完善的認知。之后，教師可以按照如此方式，引導學生探尋正方形的特點。甚至，教師可以引導學生操作電子白板，改變長方形的一邊長，不斷測量長度。在操作的過程中，學生借助具體的數據可以發現，當長方形的長和寬同樣長時，會變成一個正方形，由此發現長方形和正方形的關系——正方形是特殊的長方形。學生由此便可在腦海中建立深刻的印象，建構完善的認知結構。

2.以數輔形，證明圖形問題

證明離不開嚴密的邏輯推理。一般情況下，經過證明的結論是具有科學性的。一些圖形問題雖然可以通過直接觀察得出結論，但仍需要借助數證明，使結論更準確、科學。所以，小學數學教師應引導學生用數來證明圖形問題。

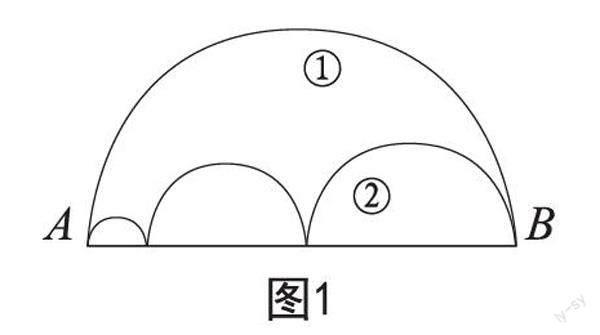
例如，在學習“圓”后，學生會面對這樣的證明（如圖1）：某人從A點走到B點，有兩條路可選，分別為①和②，哪一條路更近？為什么？

經過一番觀察，學生會提出猜測。在學生觀察后，教師可以引導學生使用賦值法，賦予大圓和三個小圓不同的直徑。通過閱讀題目，學生很容易發現，比較路程的遠近其實就是在比較半圓的弧長。因此，學生可以遷移已有認知，借助圓的周長計算公式列出算式，得出結論——兩條路一樣長。通過用數來證明形，學生可以輕松解決問題。此外，在解決問題的過程中，學生受數形結合思想的影響，能夠掌握以數輔形法，用轉化數與形來解決數學問題，提高數學學習水平。

三、結束語

總而言之，數形結合思想是學生學習數學的助力。學生通過掌握、應用數形結合思想，既可以降低數學學習難度，提高數學學習興趣，還可以扎實掌握數學知識，獲取數學學習方法，積累數學學習經驗，增強思維能力，優化認知結構，提高問題解決能力，培養審美情操。基于此，小學數學教師應注重滲透數形結合思想，以日常教學為依托，以教學需要為依據，借助數與形的關系引導學生學習數學概念、解決數學問題，做到以形助數，以及用數來感知圖形特點，證明圖形問題，做到以數輔形，發展數學學習能力，實現數學學習提質增效。

參考文獻

劉菲菲.關于在小學數學課堂中運用數形結合思想的策略研究[J].天天愛科學（教學研究），2023（5）：19-21.

陶悠悠.新課改背景下小學數學教學中數形結合思想的應用策略研究[J].教師，2023（10）：48-50.

趙楊鑫.核心素養下小學數學數形結合思想的融入與運用[J].亞太教育，2023（3）：61-63.

寧愛榮.“數形結合”思想在小學中高年級數學教學中的應用[J].學周刊，2022（36）：40-42.

朱祝梅.小學數學高段教學中數形結合思想的滲透與實踐[J].讀寫算，2022（28）：61-63.

陳海霞.數形結合思想在小學數學教學中的運用策略[J].數學學習與研究，2022（23）：65-67.

作者簡介：陳玉榮（1984.10-），女，貴州貴陽人，任教于貴州省貴陽市云巖區第一小學，一級教師，本科學歷，曾榮獲區、市級“教壇新秀”“名師”“骨干”稱號。