“質疑”與“建模”素養下對“尺縮鐘慢”證明的再討論
談元凱
(上海市洋涇中學 上海 200122)
陳 辰
(上海市第八中學 上海 200011)
1 前言
2021年9月始,上海在高一年級全面推行了新教材與新課標.其中在滬科版必修二的教學安排中,設計了“相對論初步”這一節.需要學生在學習過高中力學的全部內容后理解牛頓運動定律的局限性,并且還要知道一些關于狹義相對論的初步概念.
結合新課標核心素養的相關要求,教師可以在教學時適當對部分學有余力的學生提出一些較為靈活和高要求的學習方式.這里結合物理核心素養中“質疑”精神和“建模”能力這兩大要素[1],對教材中“尺縮鐘慢”效應的證明與推導做一個再討論.
2 教材中“尺縮鐘慢”的證明
2.1 “鐘慢”效應的證明
在“鐘慢”效應的證明方面,教材是這樣敘述的[2]:
如圖1(a)所示,假設一高鐵列車沿直線軌道以勻速v向右運動,車廂地板上一個光源向上發出一個閃光,被車廂頂部的反射鏡反射回車廂底板,并用一個鐘記錄下光脈沖來回運動經歷的時間.
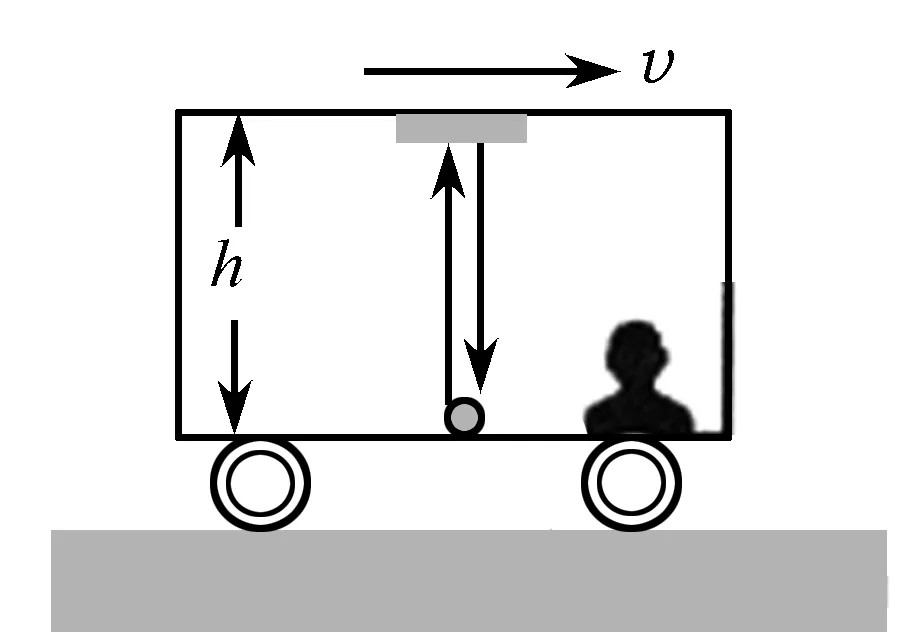
(a)

(b)圖1 “鐘慢”效應分析圖
假設車廂高度為h,因為光速為c,所以車廂里觀察者看到的時間間隔為
(1)
在地面上的觀察者看來,當光脈沖向上傳播和返回時,車廂同時在以勻速v向右運動,因此光脈沖的路徑是等腰三角形的兩條斜邊,如圖1(b)所示.
如果光脈沖來回的時間間隔是Δt′,則有
消去h后可得
(2)
由于v 故 Δt′>Δt 在“尺縮”效應的證明方面,教材是這樣敘述的: 如圖2(a)所示,在直桿的一端裝上激光發射器和接收器,另一端裝上反射鏡.當發射器發出激光被反射鏡反射回接收器時,記錄下激光往返的時間間隔Δt,即可得到直桿的長度為 圖2 “尺縮”效應分析圖 即 (3) 假設直桿所在的參考系相對地面以勻速v向右運動,如圖2(b)所示.如果地面觀察者測得的直桿長度為L′,設激光從直桿左端發出到達反射鏡的時間為Δt′1,因為在這段時間內直桿向前運動了vΔt′1的距離,因此有 (4) 同理,設激光從反射鏡返回接收器的時間間隔為Δt′2,如圖2(c)所示.在這段時間內直桿向前運動了vΔt′2的距離,因此有 (5) 因此,地面觀察者測得總的時間間隔為 Δt′=Δt′1+Δt′2= (6) 注意到Δt′是地面觀測者測得的激光從發出到接收的時間,Δt是相對直桿靜止的觀測者測得的相應的時間間隔.根據前面討論的時間的相對性,兩者滿足關系式(2). 將式(3)、(6)代入式(2)可得 (7) 由于v 故 L′ 通過閱讀教材中的證明過程可以發現,在證明“尺縮鐘慢”效應的過程中,教材建立的模型都是光線傳播的往返過程[2]. 通過思考,可以提出這樣的疑問:如果研究光線傳播過程中的某一單向過程,能否得出“尺縮鐘慢”的相對論效應呢? 在圖1(a)中,如果只考慮光線的單向傳播過程,車廂里觀察者看到光脈沖從發出至射到車廂頂部反射鏡的時間間隔為 (8) 圖1(b)中,在地面上的觀察者看來,當光脈沖傳播時,光脈沖從發出至射到車廂頂部反射鏡的時間間隔是Δt′,則有 消去h后可得 (9) 可以發現,式(9)與式(2)完全相符.說明無論取光線的單向傳播過程還是往返過程,得到的相對論效應的結果是一樣的,即:一個靜止的觀察者會發現勻速運動的參考系中所有過程都變緩了,而在這個參考系中的觀察者卻認為一切正常. 在圖2(a)中,如果發射器發出激光射到反射鏡上時所用的時間為Δt,即可得到直桿的長度為L=cΔt,即 (10) 假設在圖2(b)中直桿所在的參考系相對地面以勻速v向右運動,地面觀察者測得的直桿長度為L′,設激光從直桿左端發出到達反射鏡的時間為Δt′,考慮這段時間內直桿向前運動了vΔt′的距離,因此有 (11) 考慮到相對論的時間修正,滿足 將式(10)、(11)代入式(2)可得 (12) 綜上所述,同樣取了光脈沖單向的傳播過程,為什么不同的相對論效應做出來的結果是不同的呢?時間修正完全與教材的證明結果一致,但長度修正雖然能定性看出在“縮短”,但是和教材的表達式完全不同. 如圖3所示,有兩個一維慣性參考系S和S′.其中慣性參考系S沿著x軸以勻速v相對于S′系向右運動.以兩個慣性參考系的原點相重合的瞬間作為計時的起點,某時刻有一事件發生在點P,從S系看,P點的位置坐標為x,從S′系看,P點的位置坐標為x′.愛因斯坦從狹義相對論的基本原理出發,導出了在S系中位置坐標的洛倫茲變換[3],滿足 圖3 洛倫茲坐標變換 實際上,空間中任何物體的長度應該是同一時刻觀測到的物體兩端點之間的位置坐標之差.所以如果以光的單向傳播作為研究過程的話,起點和終點為兩個不同的坐標,在相對論效應下觀測到的結果都發生了變化,而地面觀測者看到的直桿長度其實是兩個端點的坐標之差. 所以教材中為了避免兩個坐標都發生變化引起的偏差,巧妙地設計了往返過程,起點終點都是同一個點,所以只牽涉了一個坐標的洛倫茲變換. 如果依舊要選用光的單向傳播作為研究過程,就必須同時對兩個端點的坐標進行變換,可以做如下推導. 如圖4所示,在光線單向傳播過程中,從直桿所在的參考系S來看,直桿的長度應該為L=x2-x1.從地面上的觀察著來看,直桿的長度應該為 圖4 洛倫茲變換下的“尺縮”效應 L′=x′2-x′1 根據洛倫茲變換有 則 化簡后得 (13) 可以發現,根據洛倫茲變換,同時修正直桿初、末坐標的表達式,得出的結果與教材中利用光線往返運動獲得的結論完全一樣. 而在“鐘慢”效應中,在運動的高鐵車廂里由于教材設計的研究過程是光線豎直射出,與高鐵的水平運動方向垂直,所以在這個方向上長度不會受到相對論效應的影響,即便換成單向性的過程,運算的結果也和往返過程得出的結果沒有任何差異. 對于教材的處理,無論是教師備課還是學生學習,都要反復精讀教材中的內容,閱讀的同時需要不斷思考教材的行文邏輯和編寫意圖. 本文從教材中“尺縮鐘慢”效應證明的角度出發,對課本的證明過程提出質疑,通過對比教材選取的物理過程與自己建立的物理過程中在推理上的差異,進一步明確了如何通過建模、分析、推理去描述狹義相對論中的“尺縮鐘慢”效應. 從教研、備課的角度來說,本文的再討論可以是作為課堂教學以及各位同行在備課時對于這一章節的教學參考資料. 從教學的角度來說,結合單元教學設計,本文的論述可以作為一次單元教學設計的單元作業,學生在理解了狹義相對論的基本原理和“尺縮鐘慢”效應后對于教材上的一些證明去探究新的研究方式,提出疑問的同時也展開研究,查閱資料做出合理的論述,這也是提升學生核心素養的一次機會.2.2 “尺縮”效應的證明
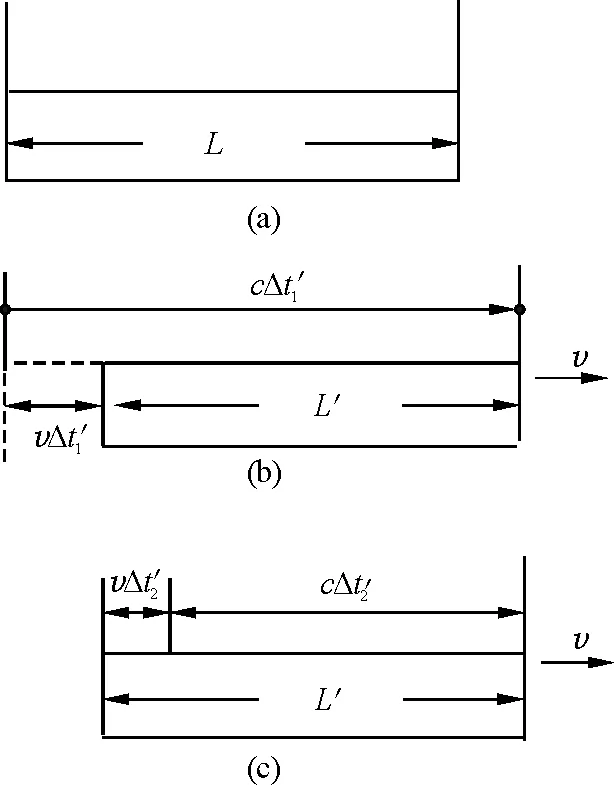
3 對教材中證明過程的質疑
3.1 對“鐘慢”效應的質疑和論述
3.2 對“尺縮”效應的質疑和論述

4 對兩種建模過程的再論述
4.1 洛倫茲變換

4.2 單向過程建模中存在的問題及原因闡述

5 結束語

