從“關聯速度”看“合成法”求勻強電場的電場強度

尚振玉

(烏魯木齊市第二十三中學 新疆 烏魯木齊 830000)

1 “合成法”簡述

勻強電場的電場強度為

(1)

已知平行于某個平面的勻強電場中3個點的電勢,利用式(1)求出兩個不同方向上的分場強,再對這兩個分場強進行矢量合成即可求出勻強電場的電場強度[1].

【例1】(2017年高考新課標Ⅲ第21題改編)勻強電場的方向平行于xOy平面,平面內a、b、c3點的位置如圖1所示,3點的電勢分別為10 V、17 V、26 V.試求該勻強電場的電場強度.

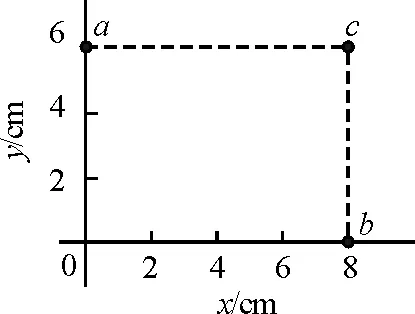
圖1 例1題圖

如圖2所示,由式(1)可知,對c點有:沿ca方向的電場強度

圖2 c點場強分析

沿cb方向的電場強度

利用平行四邊形法則合成,勻強電場的電場強度

2 發現問題

如圖3所示,同理可知,對a點有:沿ba方向的電場強度Eb a及ca方向的電場強度Ec a,利用平行四邊形法則合成,勻強電場的電場強度為E2.

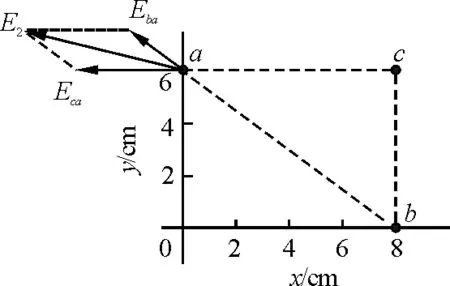
圖3 a點場強分析

空間中的勻強電場是唯一的,顯然E1和E2彼此是矛盾的,此時就會有教師和學生產生這樣的想法,平行四邊形法則對a點失效了[2].文獻[3]認為電場強度在同一個坐標系只能分解為兩個互相垂直的分場強,而不能像其他矢量一樣任意分解.為了能夠更好地解釋平行四邊形法則對a點失效的原因以及電場強度可否像其他矢量一樣任意分解,筆者通過類比的思想,以“關聯速度”為切入口探尋平行四邊形法則“失效”的原因[4].

3 問題辨析

【例2】圖4所示為在平靜海面上兩艘拖船A、B拖著駁船C運動的示意圖.A、B的速度分別沿著纜繩CA、CB方向,A、B、C不在一條直線上.由此可知C的速度方向在Ⅰ、Ⅱ、Ⅲ哪個區域?

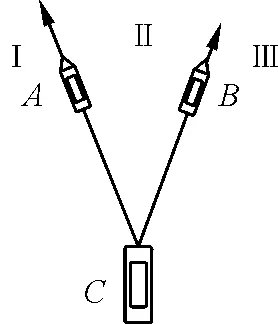
圖4 例2題圖

船C的速度與兩根繩同時存在關聯,對于這種多關聯問題,我們解決的方法是各關聯各的.由于纜繩不可伸長,船C沿著繩子靠向船A的同時還要繞船A轉動,因此C的速度在CA方向的投影與A的速度相等;同理可知船C沿著繩子靠向船B的同時還要繞船B轉動,因此C的速度在CB方向的投影與B的速度相等,所以船A的速度vA、船B的速度vB以及C船的速度vC三者之間并非合速度與分速度的關系,而是投影關系;故而在尋找vC的方向時,若已知vA與vB,并非利用平行四邊形法則求解vC,應通過投影關系求解vC.

解析：由投影關系可知,過vA作垂線PP′,過vB作垂線QQ′,則vC的末端在PP′和QQ′的交點處.因船A、B的速度大小未知,圖5所示為vA明顯大于vB時vC的方向.

圖5 vA明顯大于vB時的分析圖示

圖6所示為vA的大小接近vB的大小時vC的方向;圖7所示為vA明顯小于vB時vC的方向,所以例題2的答案是3個區域都有可能.

圖6 vA大小接近vB時的分析圖示

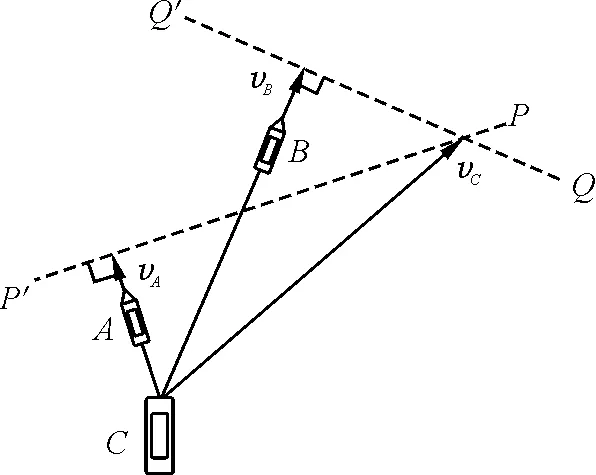
圖7 vA的大小明顯小于vB時的分析圖示

在勻強電場中使用式(1)求解電場強度時,我們要注意公式對d的要求是:沿著電場強度方向的距離.在例1中勻強電場的場強方向是未知的,那么由式(1)得出的場強Ec a、Eb a、Ec b與空間中的勻強電場E之間的關系就需要辨析清楚.

辨析1:矢量必滿足平行四邊形法則,電場強度是矢量,所以可將電場強度沿著任意兩個方向進行分解,如果兩個分量的方向是確定的,那么這兩個分量的大小也是確定的,如圖8所示.

圖8 平行四邊形法則

辨析2:在式(1)中,若d不是沿著電場方向的距離,此時計算出的電場強度是空間中勻強電場的場強在d所在方向上的投影,而非分場強,證明如下.

如圖9所示,空間中存在水平向右的勻強電場E,在空間中任取a、b、c3點,過b點作電場線的垂線,其中ab1在電場線上,ac方向延長線交bb1于b2,即b、b1、b2在同一個等勢面上.

圖9 辯析2證明

由式(1)可知,勻強電場的電場強度

ab方向的電場強度

ac方向的電場強度

其中

Lab1=La bcosα=Lab2cosβ

可得

Ea b=EcosαEa c=Ecosβ

即Ea b是勻強電場E在ab方向上的投影,Ea c是勻強電場E在ac方向上的投影;再將勻強電場的電場強度E沿著ab方向和ac方向分解,ab方向的分場強為E1,ac方向的分場強為E2,則

所以勻強電場在ab和ac方向上的投影場強Ea b、Ea c與ab和ac方向上的分場強E1、E2是不一樣的,當且僅當兩個分場強相互垂直時與投影場強相等,其他角度關系并不相等.

綜上所述,使用式(1)計算場強,d不是沿著電場方向的距離時,得出的電場強度是勻強電場在d方向上的投影;所以“合成法”中的“合成”二字本質理解應為投影關系而非矢量合成關系.

4 舊題新解

在根據投影關系求解勻強電場的電場強度有兩個投影關系時,可類比速度關聯問題中的多關聯情境.在例1中,對于a點,已知投影場強Ec a和Eb a兩個大小及方向,分別作出Ec a和Eb a的垂線,則Ec a和Eb a垂線的交點即為勻強電場的末端,如圖10(a)所示,Eb a與水平方向成37°,設E與水平方向成α,則有

(a)

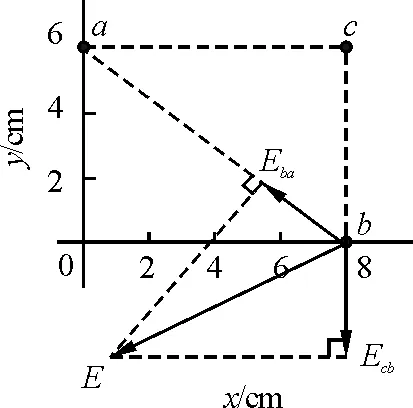
(b)圖10 例1新解圖示

解得

E=2.5 V/mα=37°

再對b點,已知投影場強Eb a和Ec b兩個大小及方向,分別作出Eb a和Ec b的垂線,則Eb a和Ec b垂線的交點即為勻強電場的末端,如圖10(b)所示, 則

解得E=2.5 V/m,α=37°,與由a點求解結論一致.

5 變式演練

【例3】如圖11所示,a、b、c、d是圓O上的4個點,空間內勻強電場的方向與圓所在平面平行,ab=5 cm,cd=8 cm,∠bac=60°,已知a、b、d3點電勢分別為φa=46 V、φb=21 V、φd=10 V,求電場強度.

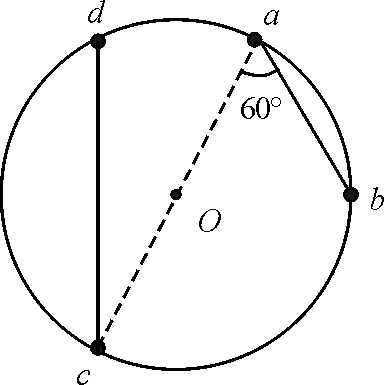
圖11 例3題圖

解析：由幾何關系可知圓半徑r=5 cm,ad=6 cm, ∠cad=53°,對a點,勻強電場在ab和ad方向上的投影強度

應用投影關系分別作出投影電場強度Ea b和Ead的垂線,如圖12所示,解得E=10 V/ cm,方向沿直徑由a指向c.

圖12 例3解析圖

6 總結與反思

(1)電場強度是矢量,矢量必然遵循平行四邊形法則,因此,我們可以使用平行四邊形法則將電場強度按照任意兩個方向進行分解.

(2)勻強電場中使用式(1)計算電場強度時,d必須是沿著電場方向的距離;若d不是沿著電場方向的距離,此時得出的電場強度是勻強電場在d方向上的投影.

(3)在勻強電場中,勻強電場的電場強度可以向任意方向進行投影,即投影電場可以有無數個,每一個投影電場的大小僅由這個方向決定,從式(1)定義上我們可以說投影電場是描述電勢在這個方向上降低快慢程度的量.如果將勻強電場的電場強度分解到兩個不同的方向上,那么這兩個方向上的分場僅在相互垂直時與這兩個方向上投影電場的電場強度大小相等.

(4)已知兩個投影電場的電場強度求解勻強電場的電場強度時,要利用投影關系分別作出兩投影電場的垂線,找到交點即為勻強電場的末端,而非將兩投影電場的電場強度進行矢量合成;存在巧合,當兩投影電場相互垂直時恰好滿足平行四邊形法則.

(5)本文以速度關聯為切入口解決“合成法”求解勻強電場的電場強度問題,對“合成法”就矢量合成這一錯誤認知進行了辨析,為合成法的使用指出了正確的理解思路——找投影關系.通過本文能夠極大地加深學生對于電場強度與電勢差之間關系的理解,有效提高學生質疑與解析的能力,培養學生物理核心素養.

(6)為避免理解偏差,將“合成法”更名為“投影法”更加利于理解,更名是否合理有待后續討論.