雷達自適應動目標顯示濾波器性能對比*

李 沙 陳元杰 蔣 俊

（1.武漢船舶職業(yè)技術學院 武漢 430033）（2.中國人民解放軍91843部隊 廈門 361003）（3.海軍工程大學電子工程學院 武漢 430033）

1 引言

運動目標顯示（Moving Target Indication，MTI）是現(xiàn)代雷達必須完成的功能之一，當前的MTI技術主要面臨雜波抑制與慢動目標檢測之間的矛盾［1］。傳統(tǒng)的MTI 技術主要利用二/三次對消器來實現(xiàn)靜止雜波的抑制，其目的是消除頻率中心為0 的固定雜波。這種抑制方式實現(xiàn)簡單，但對具有一定多普勒頻率的雜波，如海雜波，氣象雜波效果較差。為了更好地消除這種頻率中心不斷改變的雜波，一般采用自適應動目標顯示（Adaptive Moving Target Indication，AMTI）技術。將自回歸（Auto Regressive，AR）模型與FIR 濾波器進行等效，經過Yule-Walker 方程可推導出以最小均方（Least Mean Square，LMS）算法為優(yōu)化準則的AMTI濾波器，在此基礎上進一步發(fā)展出基于遞歸最小二乘（Recursive Least Square，RLS）算法的AMTI濾波器［4］。

然而，在目前公開發(fā)表的文獻中，并未發(fā)現(xiàn)對這兩種AMTI的實測數(shù)據(jù)分析。它們中哪個有更好的慢動目標檢測能力和運動雜波抑制能力，值得深入研究。

本文利用AN/TPS-70 對海警戒雷達仿真數(shù)據(jù)與海軍航空大學“雷達對海探測數(shù)據(jù)共享計劃”公開發(fā)布分享的X 波段固態(tài)全相參雷達實測海雜波數(shù)據(jù)［3］，驗證了AMTI濾波器的有效性，并對其性能進行了對比。通過實測數(shù)據(jù)發(fā)現(xiàn)：AMTI 普遍比傳統(tǒng)MTI 濾波器有更好的雜波抑制效果，且在5 級海況以下，由于海雜波的非奇異性，LMS-MTI 及其遞歸實現(xiàn)算法對海雜波的抑制效果強于RLS-MTI。

2 基于LMS的MTI濾波器

傳統(tǒng)多脈沖對消器的結構與幅頻特性如圖1所示。這是典型的FIR 數(shù)字濾波器，隨著階數(shù)的增高，其阻帶逐漸變寬，對靜止目標的抑制性能提高，同時降低了慢動目標的檢測效果，對具有一定移動速度的雜波無法有效抑制，對速度較小的目標無法有效檢測。

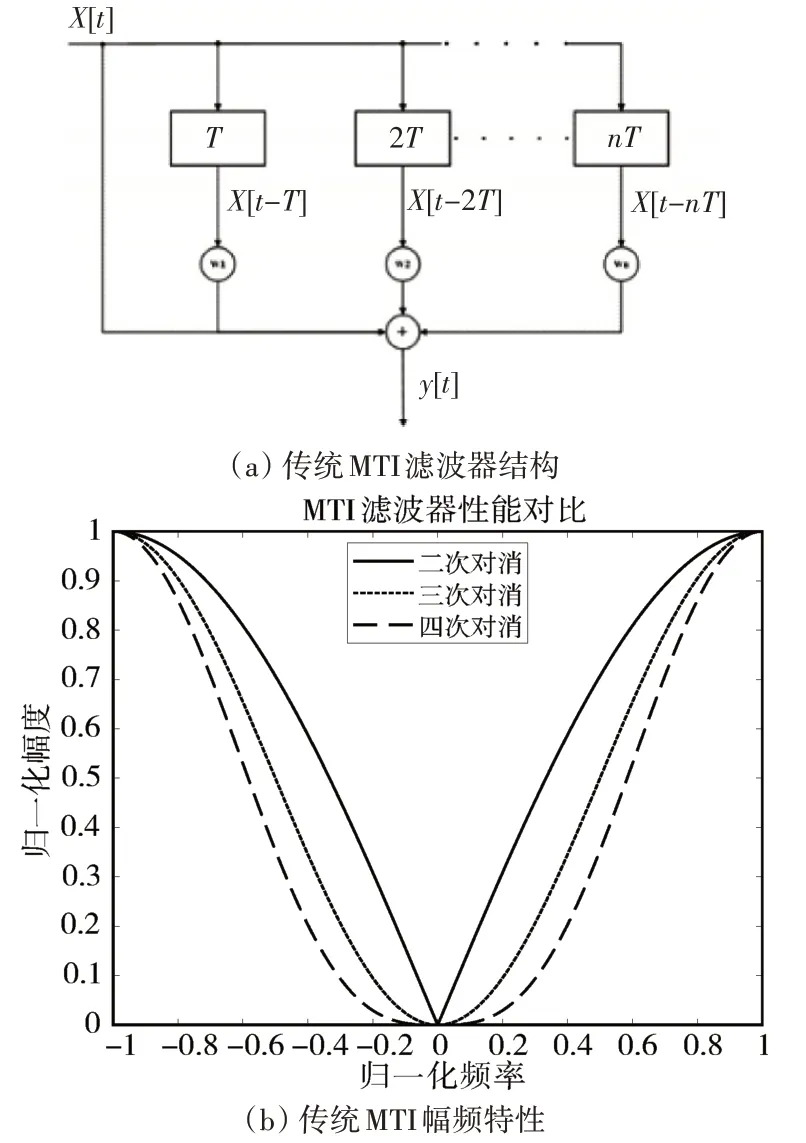
圖1 經典MTI濾波器

在雷達裝備實際工作中，單個脈沖中雜波能量遠大于目標與噪聲。基于LMS 準則的自適應濾波理論認為當濾波器權系數(shù)最佳時，雜波被大量濾除，輸出主要為有用信號分量。由于脈沖能量主要由雜波能量決定，因此只要保證輸出功率E[y2(n)]最小，就能使信雜比SCR（Signal Clutter Ratio，SCR）達到最大。該濾波過程可等效為AR 過程發(fā)生器或線性預測過程，其傳遞函數(shù)為全極點模型。利用X(t-T)，X(t-2T)，...X(t-nT)估計X(t)，使其最接近，從而達到最小。

2.1 LMS線性預測模型

基于LMS 準則的線性預測模型如圖2所示，在此假設該線性預測器為p階濾波器。

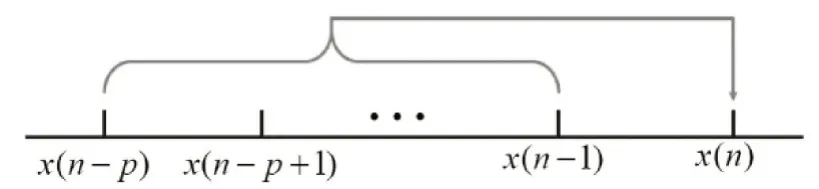
圖2 p階線性預測濾波器

對該濾波器，設有

式中rx(·)為輸入信號的自相關系數(shù)，R為自相關矩陣，α為系數(shù)矢量，r為互相關矢量。該式即為AMTI 濾波器中的維納-霍夫（Wiener-Hopf，W-H）方程，亦等效為AR 模型的尤爾-沃克（Yule-Walk，YW）方程。

2.2 LMS-MTI濾波器的遞歸實現(xiàn)

由式（4）可知，基于最小功率的MTI 本質上就是以最小均方誤差為準則的線性估計問題。然而對于m階矩陣，直接求逆在最差的情況下運算量可能會達到[2(m-1)m]m，這在實際裝備中是需要極力避免的，因此一般采用最陡下降法迭代來逼近最優(yōu)解，即沿著梯度下降的方向搜索最優(yōu)權系數(shù)［5］：

式中μ為超參數(shù)搜索步長，為使結果收斂一般取，?為一階求導符號。

將式（3）～（4）聯(lián)立，可得

式中ρmin為線性預測模型的最小均方誤差，上標H表示共軛轉置。將式（5～6）聯(lián)立，可得：

在實際應用中，利用瞬時值代替集平均值，令

可得

其結構如圖3所示。

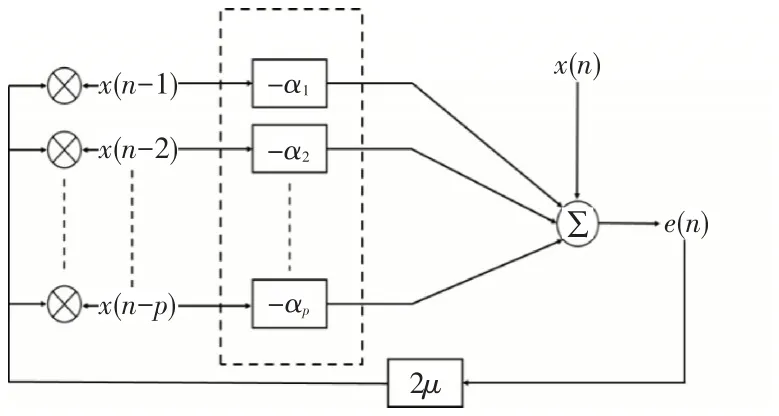
圖3 LMS-MTI濾波器結構

3 基于RLS的MTI濾波器

3.1 RLS線性預測模型

LMS線性預測模型是基于最小均方準則的，其推導基于集平均值，更適用于一類數(shù)據(jù)；而RLS 線性預測模型以最小二乘為準則，適用于本組數(shù)據(jù)［8］。在此假設該線性預測期為p 階濾波器，其數(shù)據(jù)開窗方式采用前開窗法，如圖4所示。

圖4 RLS濾波器數(shù)據(jù)前開窗法

對于RLS線性預測濾波器，設有

式中?(l，k)與z(-k)代表輸入信號時間平均自相關與時間平均互相關，該公式表明圖4 中每個濾波器權重下的數(shù)據(jù)向量與右側誤差序列向量正交。將上式以矩陣形式表示，可得：

式中Φ 為時間平均自相關矩陣，w為濾波器權值，z為時間平均互相關矢量。

為方便計算，根據(jù)線性代數(shù)理論，定義數(shù)據(jù)矩陣：

則有

將式（16）與式（13）聯(lián)立，可得：

該式即為基于最小二乘準則的濾波器權值推導公式，該濾波器的求解涉及矩陣的廣義逆求解等步驟。

3.2 RLS-MTI濾波器的遞歸實現(xiàn)

式（17）的算法復雜度大于O[(N-1)3]，與LMS-MTI 類似，實際裝備中要避免矩陣求逆的操作［5］，所以一般使用遞歸的方式逼近最優(yōu)解，在此給出遞推公式。

利用矩陣求逆引理

聯(lián)立式（18～19）可得RLS-MTI 濾波器遞歸公式：

式中g(n)為增益向量，C(n)=Φ-1(n)為逆相關矩陣。在RLS-MTI 濾波系統(tǒng)進行初始化時，一般令w(n)=0C(0)=δ-1Ι，其中δ為足夠小的正數(shù)，用以正則化，其選值與SCR 有關，Ι為單位陣。其結構如圖5所示。

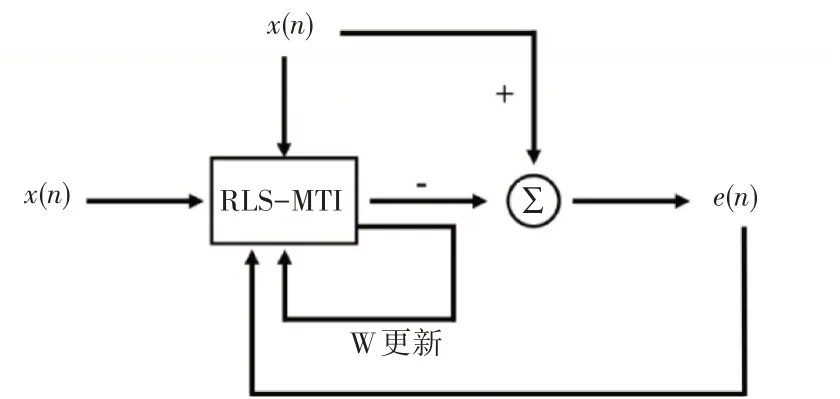
圖5 RLS-MTI濾波器結構

4 仿真數(shù)據(jù)與實測數(shù)據(jù)分析

本節(jié)通過仿真數(shù)據(jù)與實測數(shù)據(jù)評估第2、3 節(jié)中結論的有效性，并對LMS-MTI 和RLS-MTI 的性能進行對比。

4.1 仿真數(shù)據(jù)分析

仿真數(shù)據(jù)為美國AN/TPS-70對海警戒雷達，其I/Q 通道雜波振幅服從高斯分布，模值服從瑞利分布。根據(jù)其相關參數(shù)［6］，設定工作環(huán)境為濱海探測，海況為均勻海況。具體回波數(shù)據(jù)和目標信息如表1和表2所示。

表1 AN/TPS-70回波信號參數(shù)

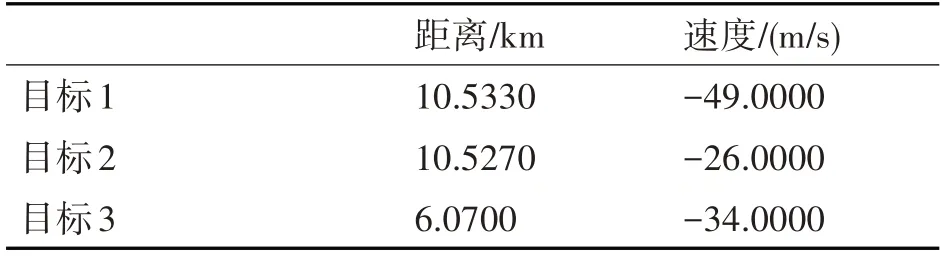
表2 目標信息

針對包含目標回波的仿真數(shù)據(jù)，采取MTI改善因子I作為雜波抑制優(yōu)劣的指標，其定義為［7］

式中SCRo表示經過雜波抑制濾波器后的信雜比，SCRi表示未經過MTI/AMTI 濾波器時的信雜比。對34 組經過脈沖壓縮后的回波，分別進行傳統(tǒng)三脈沖對消、遞歸LMS-MTI、以及RLS-MTI 處理，其濾波結果如圖6所示，對AMTI 各距離單元濾波參數(shù)取平均后，得到其幅頻特性曲線如圖7所示。具體數(shù)據(jù)如表3所示，以上濾波器均為三階FIR系統(tǒng)。

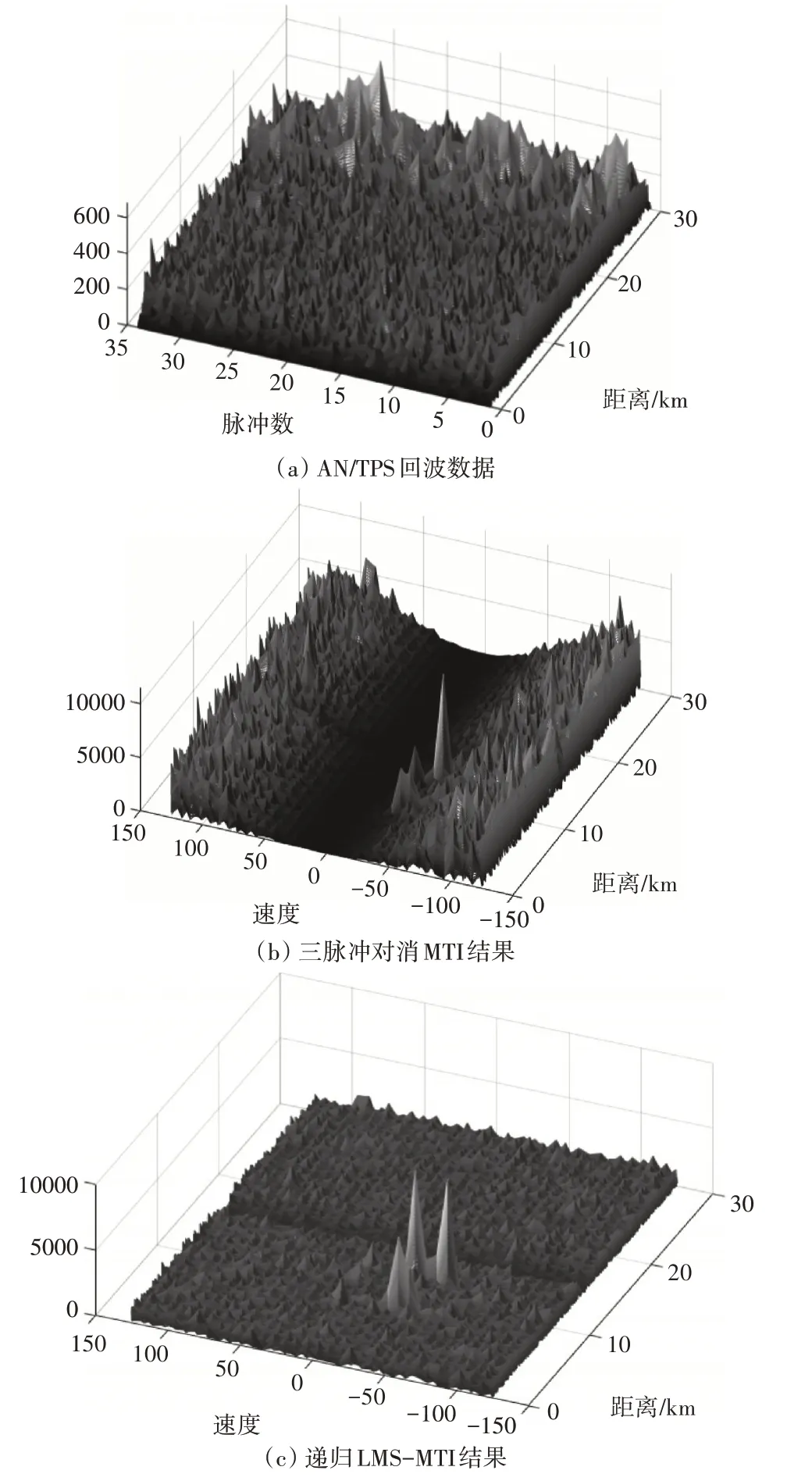
圖6 仿真數(shù)據(jù)AMTI實驗結果

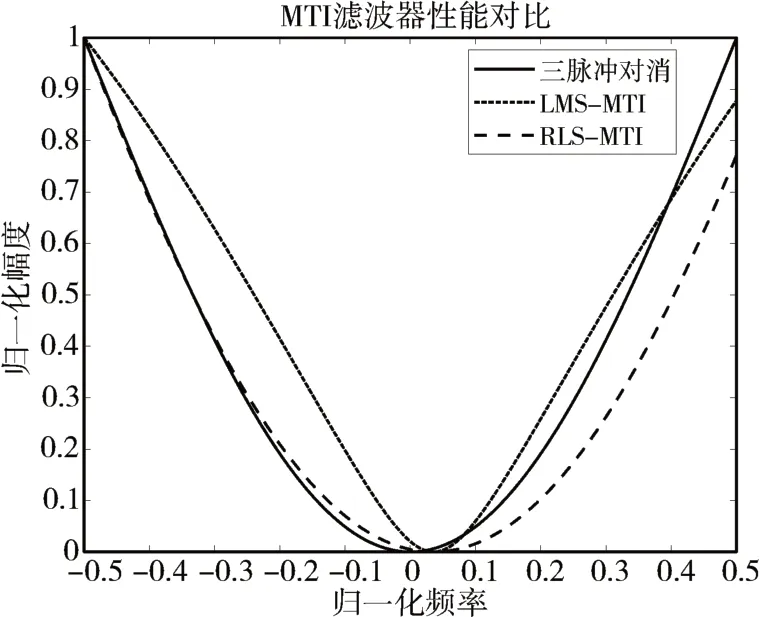
圖7 仿真數(shù)據(jù)AMTI幅頻特性曲線

由圖6 以及表3 結果可看出，傳統(tǒng)三脈沖對消器會完全抑制多普勒頻移為0 的信號，對慢速運動目標的檢測性能不好，無法抑制運動雜波并且改善因子較低。AMTI濾波器可以自動將凹口對準雜波多普勒值，自動調整濾波器各延遲線的權值，使輸出信號中雜波的成分最小，在抑制運動雜波的同時盡可能的提升信噪比。

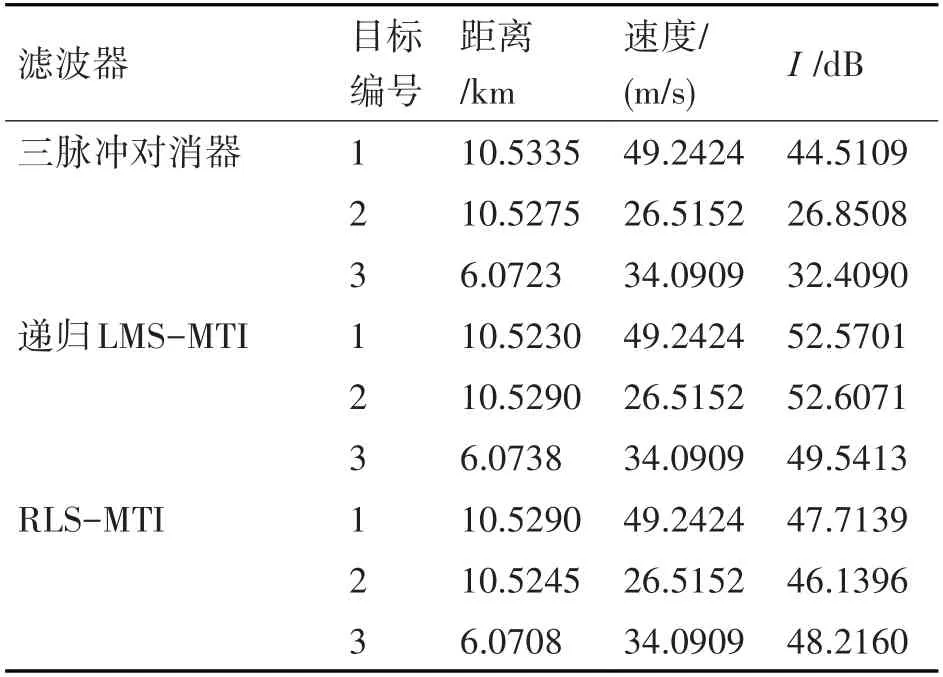
表3 仿真數(shù)據(jù)AMTI濾波性能

由圖7 及表3 結果，可知在AMTI 系統(tǒng)中，基于LMS 算法的MTI 濾波器可達到最好的運動目標檢測效果。LMS相較于RLS的濾波器凹口更準確，并且對非雜波頻率的信號有更高的幅頻響應。遞歸實現(xiàn)的自適應MTI對硬件要求更低，適用于實際裝備，靜止目標在遞歸實現(xiàn)的自適應MTI系統(tǒng)中不會被完全抵消掉。在雜波環(huán)境均勻的情況下，LMS準則相較于RLS 準則更加適合用來進行AMTI 的設計。

4.2 實測數(shù)據(jù)分析

實測數(shù)據(jù)來源于海軍航空大學“雷達對海探測數(shù)據(jù)共享計劃”第一批公開發(fā)表的X波段固態(tài)全相參雷達對海數(shù)據(jù)（本批數(shù)據(jù)主要為海雜波測量數(shù)據(jù)，無合作船只，雷達視野中有四個航道浮標）［3］。該實測數(shù)據(jù)獲取時間為2019年10月12日上午11時，實驗地點為山東省煙臺市養(yǎng)馬島，距離海邊的直線距離約50m，海拔高度約30m，雷達對海視野范圍約180°，可測得明顯海雜波數(shù)據(jù)的擦地角范圍約為0.3°～15°，當日海況等級為3 級～4 級，其實驗位置與雷達顯控截圖如圖8所示。

圖8 雷達對海探測數(shù)據(jù)采集現(xiàn)場

試驗用X波段固態(tài)全相參雷達工作參數(shù)如表4所示，經雷達地理坐標、凝視方位角與當日AIS 信息比對，在本次實驗所用數(shù)據(jù)中無合作目標，即可認為當前場景信號由海雜波與噪聲組成，因此使用雜波衰減度CA作為雜波抑制能力的性能指標［7］。

雜波衰減度的定義為［7］

式中Ci為雜波經過MTI 濾波器之前的功率，Co為雜波經過MTI濾波器之后的功率。

針對本組實測對海探測數(shù)據(jù)，分別進行傳統(tǒng)三脈沖對消、遞歸LMS-MTI、以及RLS-MTI 處理，其雜波抑制結果如圖9所示，集總平均后的濾波器頻響效應如圖10所示，具體濾波性能如表5所示，以上濾波器均為三階FIR系統(tǒng)。

通過對實測回波數(shù)據(jù)的分析處理，可從圖9、圖10 及表5 中發(fā)現(xiàn)，針對多普勒頻率中心不全為0的海雜波，AMTI 普遍比MTI 有明顯的雜波抑制效果；在5 級以下海況時，由于海雜波的非奇異性，LMS-MTI濾波器相較于RLS-MTI濾波器能夠獲得更高的雜波衰減度，LMS-MTI 在將凹口對準海雜波頻率的同時，比RLS-MTI有更強的幅頻特性。

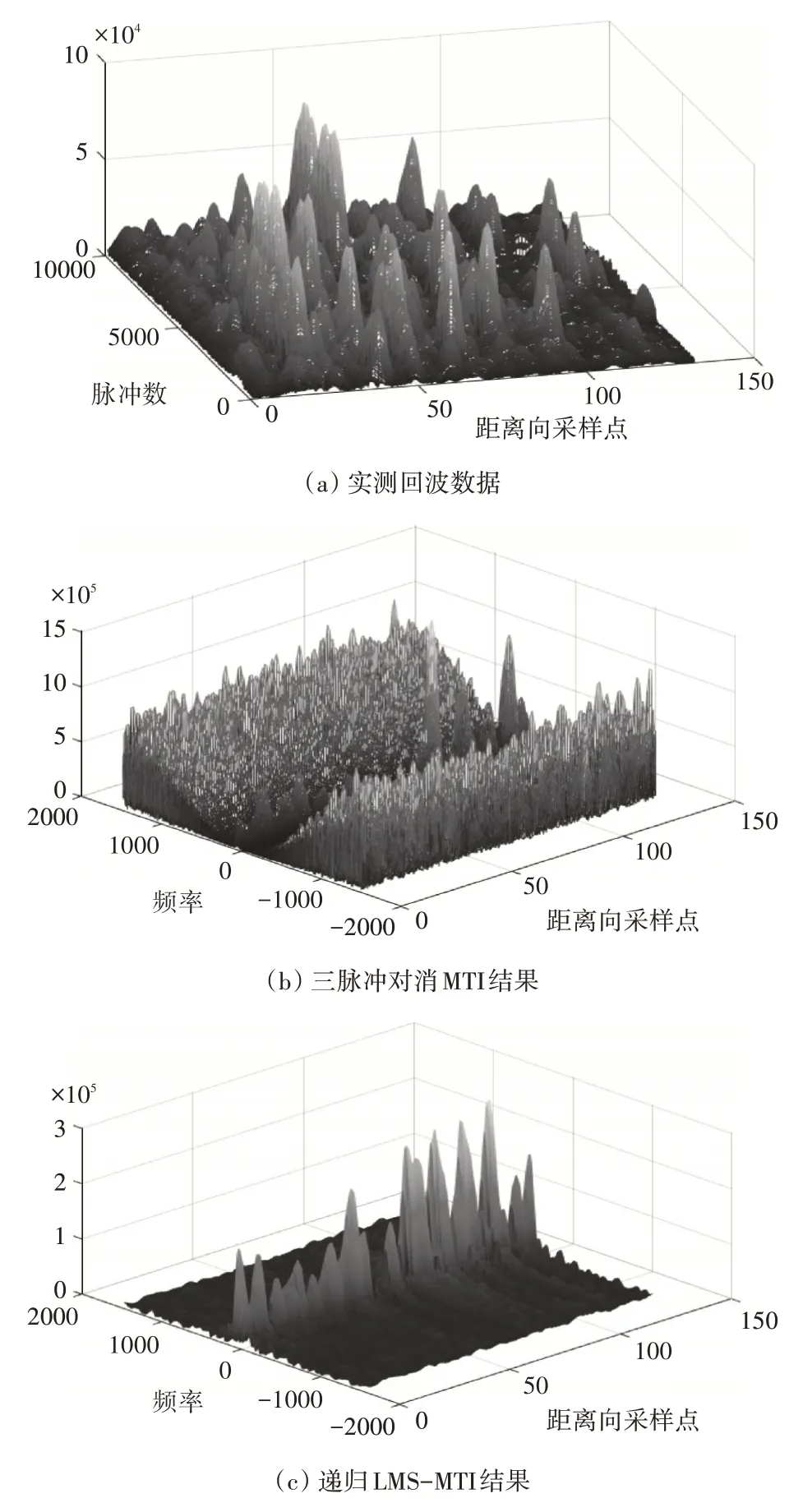
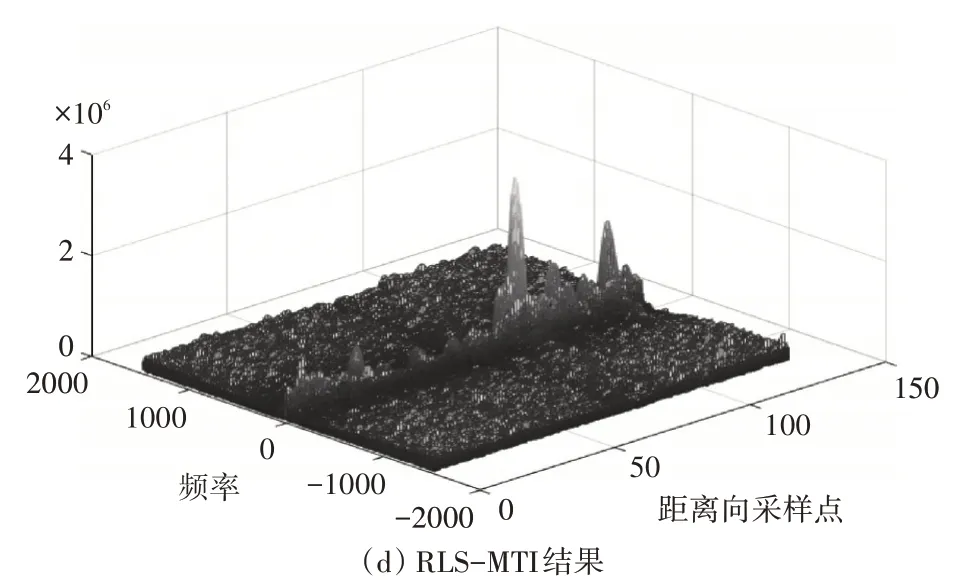
圖9 實測數(shù)據(jù)AMTI實驗結果

圖10 實測數(shù)據(jù)AMTI幅頻特性曲線

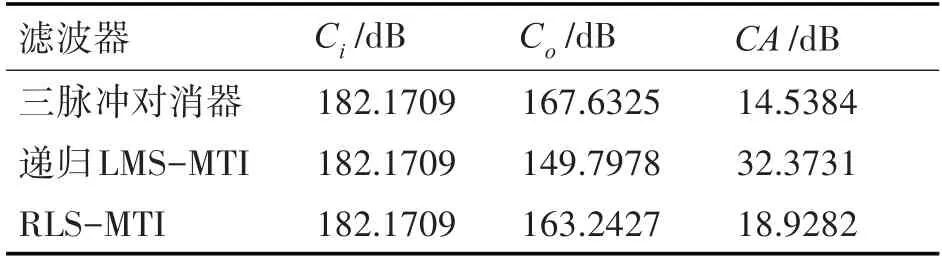
表5 實測數(shù)據(jù)AMTI濾波性能

同時，由仿真結果與實測結果可得，雜波抑制能力強與慢速目標的發(fā)現(xiàn)能力是成反比的，目前解決這一矛盾的方法是偏置相位中心（DPCA）和順軌干涉（ATI）等方法［8］，在后續(xù)的研究中將對該類MTI方式展開進一步的研究。

5 結語

本文通過AR線性預測模型與最小功率準則相結合，推導得到了LMS-MTI 和RLS-MTI 兩種自適應雜波抑制方法的遞歸實現(xiàn)公式。對仿真數(shù)據(jù)和實測數(shù)據(jù)的研究結果表明，AMTI 能夠更好地抑制海雜波，并且在5 級海況以下，由于海雜波的均勻程度較高，LMS-MTI 可以取得比RLS-MTI 更好的雜波抑制效果。在未來的工作中，仍需對高海況、非均勻條件下的海雜波進行分析，并觀察兩種自適應MTI濾波器在非平穩(wěn)背景下的工作性能。此外，還將開展海雜波背景下基于DPCA和ATI的慢動目標檢測方法。