基于演化博弈的民航高鐵競合策略研究*

景崇毅 陳 浩 劉 存

（中國民用航空飛行學院經濟與管理學院 廣漢 618307）

1 引言

近幾年來，隨著我國高速鐵路網絡的逐步擴大以及民航業的迅猛發展，2020年4月，國家發改委發布的《關于促進樞紐機場聯通軌道交通的意見》強調應加強航空公司與高鐵之間的戰略合作關系，共同打造優質的空鐵聯程聯運服務。由此，諸多航空公司開始與鐵路局進行聯合運輸，這種新型聯運模式，從根本上打破了鐵路局和航空公司長久以來的競爭發展模式，有效地將航空運輸與鐵路發運輸的優勢整合，發揮出兩者各自的優勢，為旅客出行提供了極大的便利。

從技術層面來看，高鐵優勢在于時速快、運行穩定、安全可靠；而民航優勢在于航線多樣性、精準到站、服務水平高、客運量大等優勢。此外，從成本層面來看，高鐵和民航各有其特點，民航成本低，高鐵成本相對較高。目前，學者們針對民航和高鐵之間的競爭關系開展了大量研究，研究發現高鐵和民航之間的競爭可以分為兩類：一類是以價格競爭為主的競爭，其中Li等認為民航可以在運輸旅客的成本、價格方面制定相關策略來與保持競爭優勢［4］。韋峰等通過研究不同需求下的航空公司價格反應，并在此基礎之上進一步研究了不同需求下航空公司和高鐵的競合策略［5］。萬威等通過研究發現有直達高鐵的航線更可能取消機票價格上限規制［6］。卓麗洪等通過449 個城市的面板數據研究不同距離下鐵路和民航的定價策略，在800km以內的市場中，民航對鐵路的價格和速度富有彈性［7］。李豪等通過構建Hotelling 模型分析高鐵和航空在不同定價模式下的均衡，結果表明高鐵實行動態定價能增加收益［8］。另一類是以服務質量為主的競爭。肖蕓認為民航能夠提供給旅客更優質便捷服務質量和舒適度［11］。

在民航和高鐵如何進行合作方面，駱嘉琪通過兩階段博弈理論構建高鐵和民航的競合模型，研究發現隨著運輸距離的增加，高鐵更傾向于選擇合作策略［9］。Albalate D 等通過研究高鐵對歐洲大國航空公司的影響后發現高鐵與航空運輸具有多式聯運的互補作用［10］。丁玲玲等通過采用定性分析方法對現有的空鐵聯運樞紐進行案例研究，并對空鐵聯運服務提出具體要求［12］。可鈺等通過對高鐵和民航的連續關系以及OD 可達關系進行研究，并建立OD 可達性的高鐵時刻表優化模型，進一步提升了空鐵聯運的可達性［13］。王淑偉認為空鐵聯運具有廣闊的市場空間，結合中國交通運輸網絡和需求特點，提出了“干線民航+軌道交通”這一高質量綜合運輸模式［14］。

通過以上研究可知，現有文獻在民航高鐵競合策略的研究方面取得了較多成果，但仍存在一定局限性，少有學者從演化博弈的視角來分析高鐵和民航之間的競合問題。基于此，本文通過競合博弈以及演化博弈理論構建了民航高鐵競合策略的動態演化博弈模型，通過考慮“初始合作意愿”“投入成本”“違約收益”“超額收益”“違約金”等參數對民航和高鐵策略選擇的影響，對其演化路徑及演化穩定策略的形成過程進行研究，以促進民航和高鐵的協同發展。

2 基本假設與模型構建

在民航和高鐵博弈的階段，在雙方均處于有限理性的情況下，其各自博弈策略組合為｛合作，競爭｝。本文建立假設如下：

H1：假設民航選擇合作的概率為x，則其選擇競爭的概率為(1-x)；高鐵選擇合作的概率為y，則其選擇競爭的概率為(1-y)，其中x，y∈[0，1]；

H2：在民航高鐵不選擇合作時，雙方在不同的OD 對上獨立運營，相互競爭。則民航和高鐵各自可獲得的利潤為RA和RB，其中RA＞0 和RB＞0；

H3：在民航高鐵選擇合作時，合作所獲得的超額收益為ΔR，其中民航方的超額收益分配比例為α，高鐵方的超額收益分配比例為1-α，則民航的收益為RA+αΔR，高鐵的收益為RA+(1-α)ΔR，且ΔR＞0，α∈[0，1]；

H4：在雙方簽訂合作條約之后，若其中任意一方違反合約，需向另一方繳納違約金，違約所獲得的收益為E，需承擔的違約金為Q，其中E≥Q，以民航方違反合約為例，此時民航方的收益為RA+E-Q，高鐵方合作投入為m，因民航方違約導致其收益損失n，并收取違約金Q，且Q≥m，高鐵方的收益為RB+Q-m-n；

H5：若民航高鐵選擇合作，雙方所能獲得的總收益大于其中一方選擇競爭的收益和，即ΔR≥E-m-n，此外，雙方選擇合作時各自所能獲得的收益大于選擇競爭的收益，即αΔR≥E-Q，(1-α)ΔR≥E-Q。

基于以上基本假設，可得民航高鐵競合策略演化博弈的支付矩陣，具體如表1所示。

表1 博弈雙方支付矩陣

3 民航高鐵合作的演化博弈分析

3.1 演化過程的均衡點

根據表1 可得，當民航采取“合作”策略時的期望收益為

當民航采取“競爭”策略時的期望收益為

由式（1）、（2）可得，民航的平均期望收益為

進一步可求出，民航采取合作策略的復制動態方程為

同理，高鐵采取“合作”或“競爭”的期望收益UB1、UB2、UB以及復制動態方程分別為

式（4）、式（8）聯立，可得到以下復制動態方程組：

令式（9）中F(x)=0，F(y)=0。可得出該博弈系統在二維平面s={|(x，y)|，0 ≤x，y≤1} 內有五個均衡點，分別為A(0，0)、B(0，1)、C(1，0)、D(1，1)、E(M，N)。其中，。

3.2 均衡點的演化穩定性分析

根據上文式（9）的復制動態方程組聯立求出的5 個均衡點A(0，0)、B(0，1)、C(1，0)、D(1，1)、E(m，n)。由Friedman［1］提出的理論可知，在動態演化系統中，各均衡點的穩定性可由該系統復制動態方程組的雅可比矩陣的局部穩定性分析得到。若各均衡點使得雅可比矩陣的值detJ＞0 以及跡trJ＜0，則該均衡點為空鐵聯運演化博弈的穩定策略（ESS）；當值detJ＞0 以及跡trJ＞0 時，該均衡點處于不穩定狀態；其余情況為鞍點［3］。該系統的的雅可比矩陣為

該雅可比矩陣對應的detJ和trJ分別為

其中：

3.3 演化結果分析

由表2 可知，上述各均衡點的detJ和跡trJ的計算結果可以看出，在演化過程中民航和高鐵的演化穩定策略為（合作，合作）、（競爭，競爭），其動態演化相位圖如圖1所示。

表2 各均衡點的雅可比矩陣值detJ 和跡trJ

圖1 系統演化相位圖

由上圖可知：民航高鐵合作聯運演化博弈路徑和結果取決于參與雙方的初始狀態以及鞍點位置，系統整個演化過程中存在著兩個演化穩定點A（0，0）和C（1，1）。當初始狀態位于區域ABED內時，則系統會逐步演化至A（0，0），當初始狀態位于區域CBED內時，則系統會逐步演化至C（1，1）。

3.4 演化影響因素分析

通過上述分析可知，系統穩定狀態取決于區域ABED 與區域CBED 所圍成的兩個面積SABED和SCBED，且兩個面積的大小取決于鞍點所在位置，因此針對鞍點中各個參數的影響因素進行研究。以點A、B、E、D四點圍成的區域SABED為例：

命題1：相對較高的投入成本會使得民航和高鐵更傾向于選擇競爭策略。

證明：對式SABED求關于m的偏導，可得：，則SABED隨著m的增大而增大，即當合作成本投入m逐漸增加時，高鐵和民航會逐漸選擇（競爭，競爭）策略。系統會逐漸演化到A(0，0)點。證畢。

命題2：當違約方所獲得的收益越來越大時，雙方會更傾向于選擇競爭策略。

證明：對式SABED求關于E的偏導，可得：，則SABED隨著E的增大而增大，即隨著違約方獲得的違約收益逐漸增大時，雙方背叛合作的可能性也會增大，會使得民航和高鐵逐漸傾向于選擇（競爭，競爭），此時系統會逐漸演化到A(0，0)點。證畢。

命題3：合理的懲罰機制會使得雙方更傾向于選擇合作策略。

證明：對式SABED求關于Q的偏導，可得：，SABED隨著Q的增大而減小，伴隨著違約金Q這一懲罰機制的施行，會對在合作時因一方違約所帶來的經濟損失進行補償，提升了雙方合作的積極性，此時民航和高鐵會逐漸傾向于選擇（合作，合作）策略，系統會逐漸演化到C(1，1)點。證畢。

命題4：較高的超額收益會使得雙方更傾向于選擇合作策略。

證明：對式SABED求關于ΔR的偏導，可得：，SABED隨著ΔR的增大而減小，這表明隨著超額收益值的不斷提高，高鐵和民航各自可獲得收益也會逐漸增多，民航和高鐵會逐漸傾向于選擇（合作，合作），此時系統會逐漸演化到到C(1，1)點。證畢。

4 演化仿真分析

為了更清楚地描述支付矩陣中各參數對民航高鐵選擇策略的影響，利用Matlab R2016b 軟件對相關參數進行仿真分析。

取RA=2800萬元，RB=2400萬元，ΔR=350萬元，E=150萬元，Q=80萬元，m=60萬元，n=85萬元，α=0.5。此時鞍點為（0.34，0.34）。

1）首先探究雙方初始合作意向得策略選擇動態演化的影響結果，將民航與高鐵初始狀態下選擇合作策略比例分別取（0.1，0.6），（0.2，0.7），（0.3，0.5），（0.4，0.2），（0.5，0.1），（0.7，0.5），（0.8，0.3），（0.9，0.1），具體仿真結果如圖2所示。

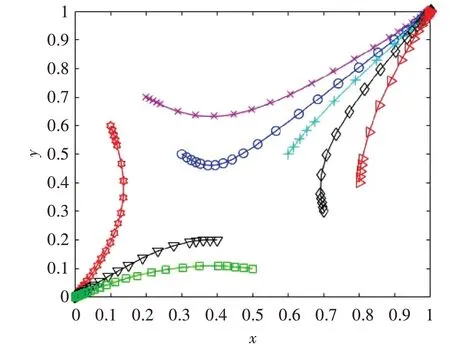
圖2 初始合作比例對策略選擇動態演化的影響

由圖2 可知，初始合作比例不同，其演化的最終結果也不相同，若雙方初始選擇合作策略比例大于鞍點，則其最終會向著（1，1）點演化，否則其最終會向著（0，0）點演化，即在演化過程中，雙方的合作意愿逐漸降低，或因一方合作意愿降低而打擊另一方的合作積極性，從而雙方最終不會達成合作。

2）保持其他條件不變，投入成本m分別取40、80，探究投入成本的變化對雙方合作策略選擇的影響結果，具體結果如圖3所示。

由圖3 可以看出，隨著投入成本m的增大，雙方的演化速度及演化結果均受到了影響，其中當m越來越小時，雙方會朝著（1，1）點演化，達成長期合作的可能性逐漸增大。當m越來越大時，雙方向著（0，0）點的演化速度變快，此時雙方更傾向于選擇（競爭，競爭）策略。

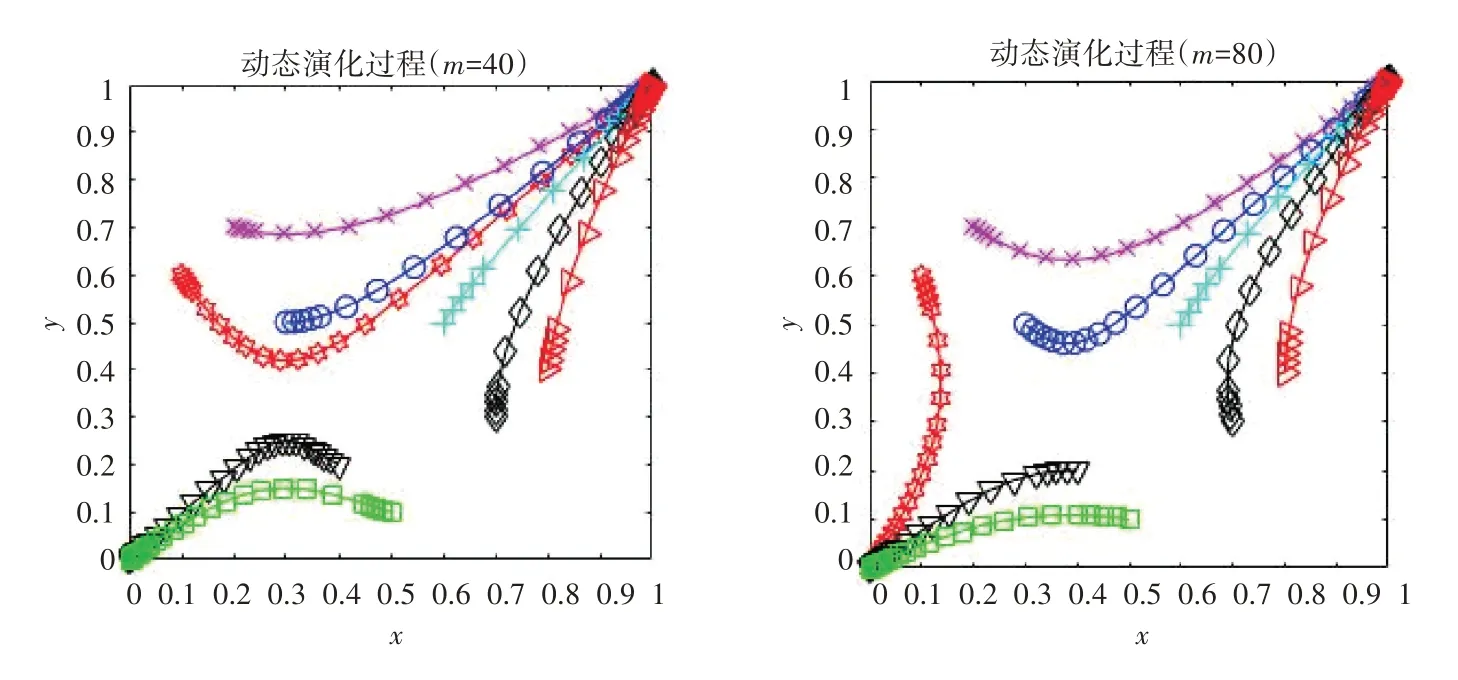
圖3 投入成本對策略選擇動態演化的影響

3）保持其他條件不變，雙方合作時因一方違約所需繳納違約金Q分別取70、90。探究違約金的變化對雙方合作策略選擇的影響結果，具體結果如圖4所示。

由圖4 可以看出，隨著違約金Q的增大，雙方向著（0，0）演化的速度越來越緩慢，此時雙方的合作積極性更高，逐漸向著（1，1）點演化，最終雙方會更傾向于選擇（合作，合作）策略。

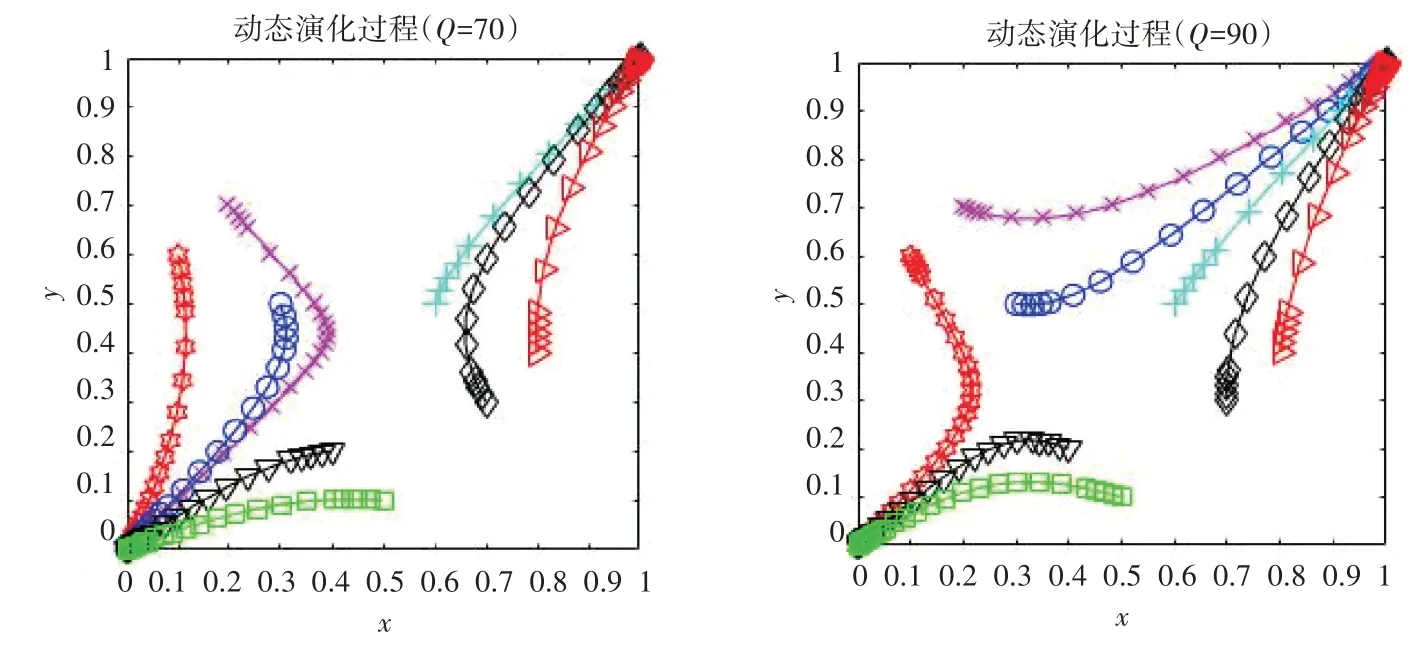
圖4 違約金對策略選擇動態演化的影響

4）保持其他條件不變，雙方在合作時一方違約所能獲得違約收益E分別取130、170。探究違約收益的變化對雙方合作策略選擇的影響結果，具體結果如圖5所示。

由圖5 可以看出，隨著違約收益的增大，雙方向著（1，1）點的演化速度越來越緩慢，此時雙方的合作積極性更低，逐漸向著（0，0）點演化，最終雙方會更傾向于選擇（競爭，競爭）策略。

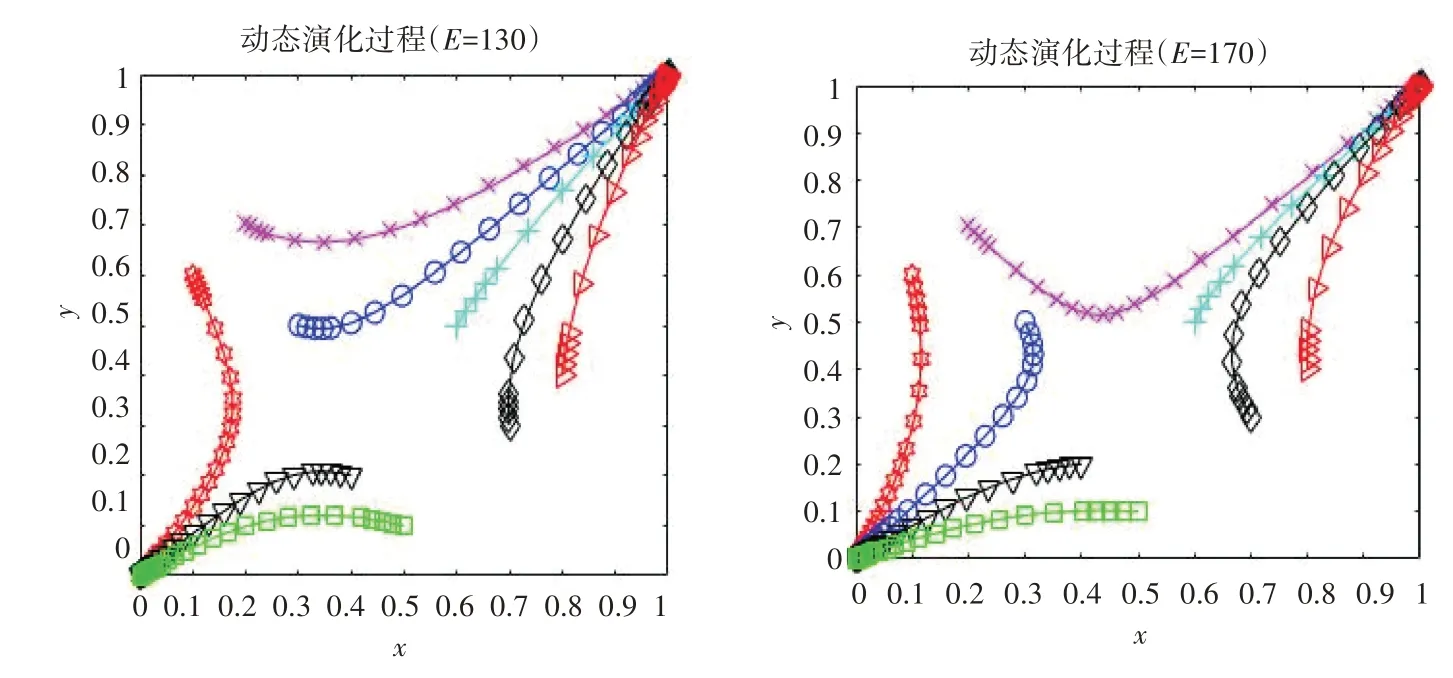
圖5 違約收益對策略選擇動態演化的影響

5）保持其他條件不變，雙方在合作時所能獲的超額收益ΔR分別取130、170。探究違約收益的變化對雙方合作策略選擇的影響結果，具體結果如圖6所示。

由圖6 可以看出，隨著超額收益的增大，雙方向著（0，0）點的演化速度越來越緩慢，此時雙方的合作積極性更高，逐漸向著（1，1）點演化，最終雙方會更傾向于選擇（合作，合作）策略。

圖6 超額收益對策略選擇動態演化的影響

5 結語

本文從影響民航高鐵競合策略的影響因素入手，首先構建了雙方選擇競合策略演化博弈模型，并在此基礎之上進一步求出雙方演化博弈的均衡解以及演化的穩定點。結合Matlab 軟件對影響雙方選擇策略的重要因素進行仿真分析，得出以下結論：

1）雙方的初始合作意愿、違約金、超額收益與合作穩定性呈正相關，雙方初始合作意愿越強，則雙方未來達成長期合作的可能性越大。違約金的存在也可以在一定程度上作為懲罰機制來保護合作的穩定性。同時超額收益越多會促進雙方合作的積極性，從而使雙方達成長期合作。

2）雙方在合作過程中的合作投入成本以及違約收益與合作穩定性呈負相關，較多的合作投入意味著雙方在選擇“合作”策略時需要承擔更大的風險。同時雙方在合作過程中一方因為違約所能獲得的收益值越高時，雙方選擇違約的可能性越大，從而不利于雙方合作的穩定性。