一致分數階時滯微分方程邊值問題解的存在性與唯一性
張 敏, 周文學, 黎文博
(蘭州交通大學 數理學院, 蘭州 730070)
0 引 言
分數階微分方程的邊值問題是分數階微分系統理論的重要課題. 目前, 對分數階微分方程邊值問題的研究已取得了豐富成果, 其中最主要的是基于Riemann-Liouville和Caputo分數階導數的定義[1-9]. 但這兩種導數均不滿足經典鏈式法則, 并且這兩種導數的某些性質使得分數階導數的應用很困難. 因此, Khalil等[10]提出了一種新的分數階導數和分數階積分的定義, 稱為一致分數階導數和積分. 這種新的分數階導數的定義可滿足經典的分數階導數不能滿足的一些性質, 如乘積法則、 商法則、 鏈式法則、 羅爾定理和中值定理等, 并且其在生物物理學、 電容理論、 控制理論和實驗數據擬合等領域應用廣泛[11-13]. 但對帶有時滯的分數階微分方程邊值問題的研究目前報道較少[14-16]. Yang等[17]利用Schaefer不動點定理和Krasnoselskii’s不動點定理研究了一類非線性分數階微分方程邊值問題
正解的存在性, 其中0 解的存在唯一性, 其中1 基于上述研究, 本文利用Leray-Schauder度理論和Banach壓縮映射原理考慮如下一類一致分數階時滯微分方程邊值問題: (1) 解的存在性與唯一性, 其中1<β≤2,τ>0,f: [0,1]×→是連續函數,是階數為β的一致分數階導數. 定義1[10]假設函數f: [0,∞)→, 則f的β∈(n,n+1]階一致分數階導數定義為 (2) (3) 注2由一致分數階導數定義可知, 當β=1時, 一致分數階導數定義即為傳統的一階導數定義. 引理1[10]當β∈(n,n+1]并且f在t>0處n+1階可微時, 有 (4) 定義2[19]假設函數f: [0,∞)→, 則f的β∈(n,n+1]階一致分數階積分定義為 (5) 引理2[19]假設函數f: [0,∞)→連續, 并且β∈(n,n+1], 則有 DβIβf(t)=f(t). (6) 引理3[19]假設f: [0,∞)→是β階可微函數, 并且β∈(n,n+1], 則有 IβDβf(t)=f(t)+a0+a1t+…+antn, (7) 其中ai∈,i=0,1,2,…,n. 引理4設函數f: [0,1]×→是連續的,u(t)是邊值問題(1)的解, 則 (8) 其中格林函數G(t,s)為 (9) 證明: 由引理3知, 有 (10) a0+a1=0; (11) 根據u(1)+u′(1)=0, 有 (12) 結合式(11),(12)可得 (13) 將式(13)代入式(10)可得 引理5(Arzela-Ascoli定理)[20]集合P?C([a,b])列緊的充分必要條件為: 1) 集合P有界, 即存在常數ψ, 使得對?u∈P, 有|u(t)|≤ψ(?t∈[a,b]); 2) 集合P等度連續, 即對?ε>0, 始終存在σ=σ(ε)>0, 使得對于?t1,t2∈[a,b], 只要|t1-t2|<σ, 即有|u(t1)-u(t2)|<ε(?u∈P). 設A為C([-τ,1],)按范數構成的Banach空間, 在A上定義一個算子Q, 假設條件: (H1) 函數f∈C([0,1]×,), 并且φ∈C([-τ,0],); (H2) 存在常數α,B>0, 使得?(t,u)∈[0,1]×, 有|f(t,u)|≤α|u|+B; (H3) 存在函數η(t)∈L1/2([0,1],+), 使得?t∈[0,1], 當任取u,v∈時, 有|f(t,u)-f(t,v)|≤η(t)|u-v|, 其中 證明: 由函數G(t,s),f(s,u(s-τ))的連續性可知算子Q是連續的, 并且易證Q(A)?A.設P是A中的一個有界集, 則存在常數M>0, 使得對任意的u∈P, 有‖u‖≤M. 下面利用Leray-Schauder度理論證明邊值問題(1)正解的存在性, 分以下3個步驟. 1) 證明算子Q(P)是一致有界的.對任意的u∈P, 有 因此, 算子Q(P)是一致有界的. 2) 證明算子Q(P)是等度連續的.對任意的u∈P,t1,t2∈[-τ,1]且t1 ① 當0≤t1 ② 當-τ≤t1 ③ 當-τ≤t1<0 在上面3種情形中, 當t1→t2時, 總有|Qu(t2)-Qu(t1)|→0, 表明Q(P)是等度連續的.故由引理5可知,Q(P)是列緊的, 從而算子Q:A→A是全連續的. 令ω=T+1,Bω={u∈A: ‖u‖<ω}, 則u≠γQu, 對任意的u∈?Bω,γ∈[0,1].定義一個映射:Fγ(u)=u-γQu, 則Fγ(u)=u-γQu≠0, 對任意的u∈?Bω,γ∈[0,1].因此, 由Leray-Schauder度的同倫不變性, 有 deg(Fγ,Bω,θ)=deg(I-γQ,Bω,θ)=deg(F1,Bω,θ)=deg(F0,Bω,θ)=deg(I,Bω,θ)=1≠θ. 從而根據Leray-Schauder度的可解性可知, 方程F1(u)=u-Qu=0在Bω上至少存在一個解, 進而邊值問題(1)至少有一個正解.證畢. 定理2如果條件(H1)和(H3)成立, 并且‖η‖(Λ2+Λ3)<1, 則邊值問題(1)存在唯一解. 下面利用Banach壓縮映射原理證明邊值問題(1)解的存在唯一性, 分以下兩個步驟. 1) 證明Q(Bδ)?Bδ.對任意的u∈Bδ, 有 則‖Qu‖≤δ.表明算子Q將Bδ中的有界子集映為Bδ中的有界子集, 即Q(Bδ)?Bδ. 2) 證明算子Q為壓縮映射.對任意的u,v∈A: ① 當t∈[0,1]時, 有 ② 當t∈[-τ,0]時, 有|Qu(t)-Qv(t)|=|φ(t)-φ(t)|=0. 由①,②可得 ‖Qu-Qv‖[-τ,1]≤‖η‖(Λ2+Λ3)‖u-v‖[-τ,1]. 因為‖η‖(Λ2+Λ3)<1, 所以算子Q為壓縮映射.即由Banach壓縮映射原理可知算子Q存在唯一的不動點, 故邊值問題(1)存在唯一解. 考慮下列一致分數階時滯微分方程邊值問題: (14) 解的存在性與唯一性. 所以存在η(t)=e-3tsin1/2t∈L1/2([0,1],+), 滿足條件(H3), 且‖η‖=0.166 7.又因為 所以‖η‖(Λ2+Λ3)≈0.571 3<1.因此根據定理2可知, 邊值問題(14)存在唯一解.
1 預備知識



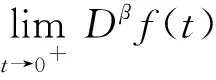




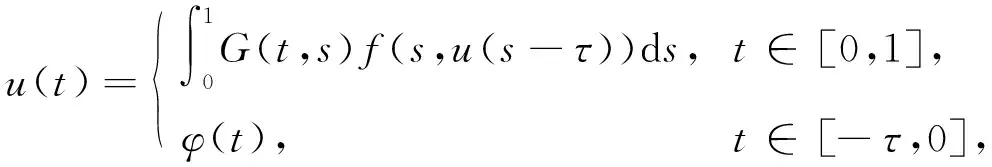
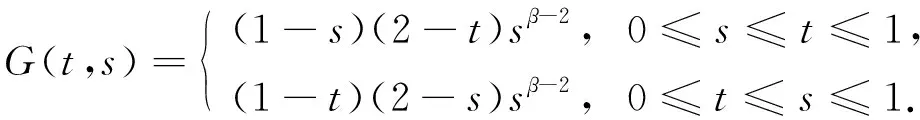
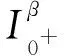



2 主要結果
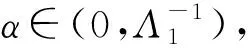
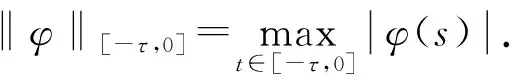
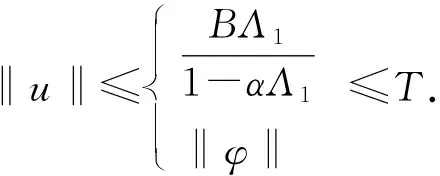
3 應用實例


