運梁車荷載作用下粗粒土填料的回彈與累積塑性應變特性研究

聶如松 ，肖玲，譚永長，黃茂桐，周徐海，饒有權

(1.中南大學 土木工程學院，湖南 長沙 410075；2.中南大學 重載鐵路工程結構教育部重點實驗室，湖南 長沙 410075；3.湖南中大設計院有限公司，湖南 長沙 410075)

高速鐵路修建時，運梁車將箱梁馱運至架梁工地的途中必然經過路基，而運梁車和箱梁的總質量可達上千噸，遠遠大于線路運營時的列車荷載。為保證路基面幾何狀態不受影響，施工單位一般先填筑基床底層和部分基床表層，待架梁完畢運梁車不再通過后，再進行基床表層的平整和壓實施工。我國南方新建鐵路規劃較多，同時南方地區雨季時間長，在長時間降雨和運梁車反復荷載作用下，新建路基車轍和沉陷明顯，路基面平整度差。如圖1所示南方某高速鐵路在運梁車反復作用之后路基出現明顯車轍。路基變形過大會直接影響路基穩定性。同時，明確運梁車荷載對路基變形和力學特性的影響也可為后續修整時確定路基的深度提供指導和依據。因此，有必要對運梁車和降雨共同作用下的路基變形特性開展深入研究。路基能有效地吸收和消散動力荷載，是承受交通動力荷載的關鍵結構。因此，準確掌握路基填料的強度及變形特性是鐵路路基設計和施工的先決條件。新建高速鐵路路基基床主要為粗粒土填料，其在承受重復交通荷載時通常表現出可恢復(彈性)變形和永久(塑性)變形。如果動荷載較大，則誘發的塑性變形在每個荷載循環內不斷累積，可能導致路基沉降過大。動三軸試驗可模擬路基填料的實際服役環境，是研究路基填料在交通荷載作用下動力特性和累積變形的重要方法。基于動三軸試驗，國內外學者針對粗粒土的變形特性和動力特性已開展較多研究。其中，BOULANGER 等[1]利用動三軸試驗研究圍壓對粗粒土累積應變的影響。冷伍明等[2-5]探討圍壓、含水率、動應力對粗粒土動強度及變形的影響，提出粗粒土填料累積變形穩定界限狀態和判別準則。龍堯等[6]分析粗粒土填料在列車荷載下產生的累積變形，并建立考慮循環應力比和圍壓的粗粒土路基累積變形模型。馬少坤等[7]以南寧地鐵區域飽和圓礫土為研究對象，分別探討相對密實度、動應力對累積應變、滯回圈和孔壓的影響。王康宇等[8]引入塑性應變率和安定理論，依據塑性應變發展規律將粗粒土試樣劃分成塑性安定、塑性蠕變和增量破壞3種類型，確定塑性安定和塑性蠕變狀態的臨界動應力水平。上述研究聚焦于鐵路線路運營狀態下路基填料的變形特性，而鐵路路基在承受列車動荷載長期作用前，需經歷運梁車的壓密作用。時興隆等[9-10]對運梁車通過期間的路基沉降進行了觀測，指出運梁車通過新建路基時，沉降速率快速增加，路基產生明顯工后沉降和不均勻沉降。但現有關于運梁車荷載對路基影響的研究局限于靜態沉降觀測。相比于高鐵列車動荷載作用，總質量達上千噸的運梁車對路基的動荷載作用更顯著，易致使路基服役性能發生劣化，甚至發生失穩破壞。因而，有必要進一步研究運梁車荷載下路基填料的變形和動力特性。鑒于運梁車往復荷載作用下路基動力特性研究鮮有報道的情況，本文針對新建高鐵路基，開展連續加載的大型動三軸試驗，探討圍壓、動應力及含水率對粗粒土填料的動力特性和變形特性的影響，建立考慮動應力和圍壓的塑性應變預測模型。研究結果可為正確認識運梁車荷載作用下路基土的變形和動力特性提供依據。

圖1 運梁車車轍圖Fig.1 Rutting diagram of subgrade surface

1 運梁車荷載測試

為獲得新建高速鐵路路基面動應力，選取典型新建高鐵路基斷面，在基床底層表面埋設BX-7型電阻應變式土壓力盒，進行現場實車測試。試驗車輛為DCY900t運梁車，車輛自身重量為318 t。車輛共有16 對輪組，輪距分別為2 200 mm 和2 800 mm，如圖2。測試過程中，DCY900t運梁車馱運自重為793 t 的32 m 簡支箱梁，以5 km/h 的速度通過路基。測得的動應力時程曲線如圖3。

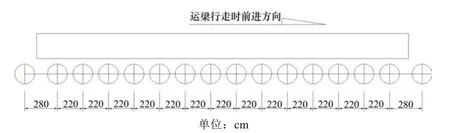
圖2 DCY900t運梁車輪胎分布圖Fig.2 Tire diagram of transporting girder vehicle

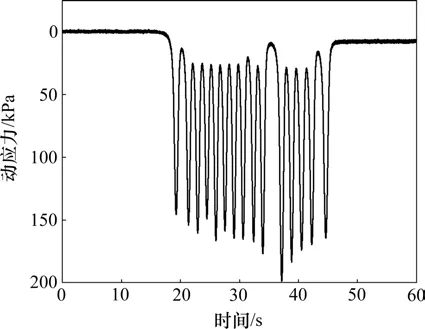
圖3 埋深0.2 m測點典型動應力時程曲線Fig.3 Typical dynamic stress time history curve of measuring point with buried depth of 0.2 m

由圖3 可知，測點的動應力具有明顯的周期性，動應力峰值與每排車輪位置對應，說明運梁車對基床的加卸荷過程由一對輪載完成。從圖3還可看出，前排車輪和后排車輪引起的動力響應較弱，動應力時程曲線呈“駝峰型”，這是因為車輪間距很小，使得每排車輪引起的動力響應表現出疊加效應。測點元件上方有厚度為0.2 m 的保護層，可忽略不計，將測點動應力視作基床頂面動應力，則運梁車荷載下路基頂面的動應力幅值集中于160～175 kPa 范圍內，動應力幅值均值約167 kPa，對動應力時程曲線進行快速傅里葉變化，獲得主頻為0.617 Hz，與根據運梁車輪對的間距以及速度確定的主頻0.63 Hz 相近，證明了現場動力測試的合理性。

運營期間傳遞到道床的高鐵列車荷載通過擴散作用散布于路基面。現有文獻中現場試驗和模型試驗測得的高鐵列車荷載下路基表面動應力一般為10～30 kPa，動應力頻率為3～5 Hz[11-13]。而運梁車荷載和高鐵列車荷載間有著很大的不同。輪胎式運梁車軸重大，輪組多，行車速度較低，且運梁車荷載直接作用于路基面，引起新建高鐵路基的荷載效應強。

2 大型動三軸試驗

2.1 試驗儀器及材料

試樣儀器及材料如圖4 所示。試驗儀器采用DJSZ-150 型大型靜動三軸試驗機，具有靜、動軸向力加載、圍壓和孔隙水壓力穩定控制功能。試驗采用的粗粒土填料取自常益長高鐵某標段路基基床底層，磨圓度較好，顏色呈淺黃色或者淺紅褐色。

圖4 試驗儀器及土樣Fig.4 Testing apparatus and soil materials

為確定試驗用土的物理力學性質指標，開展顆粒分析試驗與擊實試驗。土樣的顆粒級配曲線見圖5，根據顆粒分析試驗結果確定土樣為級配不良的間斷級配中圓礫B1 填料。物理性質參數如下：不均勻系數Cu=31.05；曲率系數Cc=0.63；最大干密度ρdmax=2.31g/cm3；最優含水率ωopt=6.35%。此外，開展靜三軸試驗得到粗粒土最優和飽和含水率下黏聚力c分別為63.7 kPa 和43.6 kPa，內摩擦角φ分別為36.2°和30.8°。

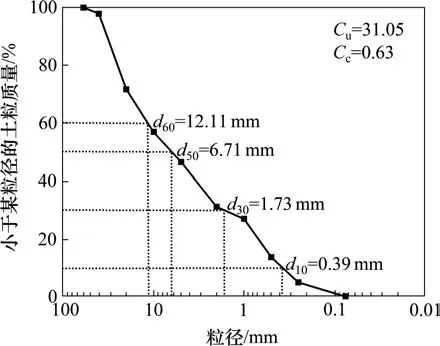
圖5 粗粒土顆粒級配曲線Fig.5 Grain-size distribution curves of the coarse-grained soil

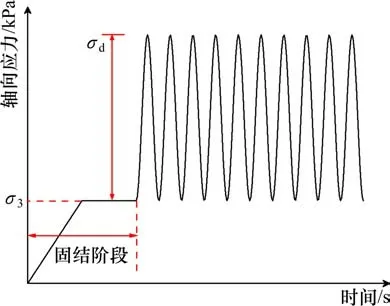
圖6 軸向應力時程示意圖Fig.6 Schematic diagram of axial stress time history

2.2 試驗參數及方案

依據《高速鐵路設計規范》(TB 10621—2014)，當基床底層選擇粗粒土作為填料時，壓實系數不小于0.95。故選擇0.95 作為試樣的壓實系數K。鐵路路基土體在進行回填時在最優含水率附近壓實，考慮到路基土體含水率易受到環境變化而發生改變，甚至達到飽和狀態，選取最優含水率(6.35%)和飽和含水率(9.10%)2種狀態。高鐵路基處于淺埋深、低圍壓的應力狀態，故試樣的圍壓σ3取30，60 和90 kPa，以模擬不同深度處路基填料的側壓。采用頻率為0.5 Hz 的正弦波荷載模擬運梁車荷載，設置動應力幅值σd分別為90，120，150 和180 kPa。試驗采用固結不排水剪，動三軸試驗方案見表1。

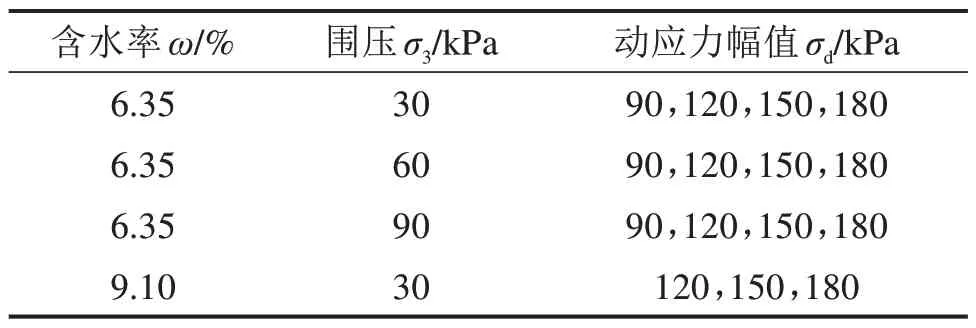
表1 動三軸試驗方案Table 1 Test scheme of dynamic triaxial test

試樣嚴格按照《土工試驗方法標準》(GB/T 50123—2019)的要求制作。為保證試樣壓實度均勻，分6 層擊實制樣，制備直徑為300 mm，高度為600 mm 的試樣。飽和試樣采取真空和水頭飽和方法使其達到飽和狀態。先對試樣抽真空在壓力室內飽和，之后再進行水頭飽和，利用水頭差使得水流從試樣底部流向試樣頂部，最后進入體變管，以飽和試樣。施加圍壓，計算孔隙壓力系數B值，飽和度控制在95%以上。等壓固結，當孔壓逐漸消散，小于1 kPa 時，則認為固結結束。隨后，關閉排水閥門，施加正弦動荷載，振動次數設定為10 000 次。在動應力波谷處，軸向偏應力的最小值為0 kPa(新建高鐵路基尚未鋪軌，不考慮上部結構對路基的靜偏應力作用)，在動應力波峰處，軸向偏應力的最大值為σd。試樣破壞標準為軸向應變達到5%。

3 動應力-應變滯回圈分析

滯回圈為一個荷載周期內試樣受到的動應力和所產生的動應變之間的關系曲線。為分析滯回圈演化規律，繪制典型穩定型試樣(ω=6.35%；σ3=30 kPa；σd=180 kPa)的應力-應變關系曲線。值得注意的是，為節約儲存空間，本文只選取部分振次數據進行繪制，如圖7所示。滯回圈間距隨荷載循環次數的增加而逐漸變小，滯回圈逐漸趨于緊密，不再向軸向應變發展方向移動或移動微小，土體處于彈性穩定狀態。且滯回曲線斜率逐漸增大，說明軸向應變雖不斷發展，但在軸向壓縮的同時也使土顆粒更加緊密，粗粒土試樣剛度有所增加。

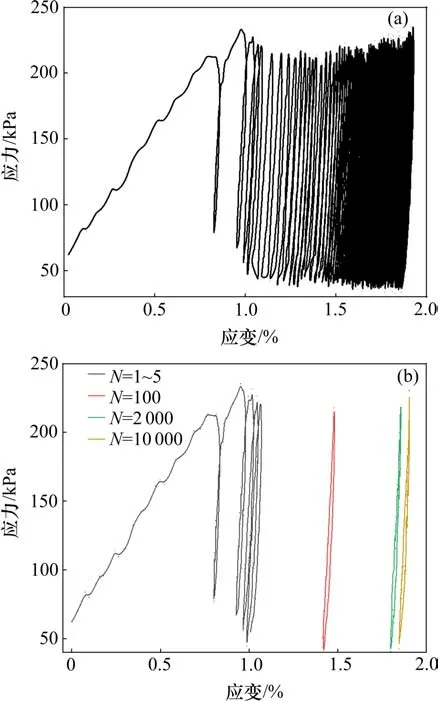
圖7 穩定型試樣滯回曲線Fig.7 Dynamic stress-strain curves of stable specimen

分析滯回圈形態可知，壓實粗粒土在循環荷載作用下動應力-應變關系曲線表現出明顯的變形積累性、滯后性和非線性。剛開始加載時滯回圈的不閉合程度和面積都較大，但隨著振次增加，滯回圈從比較“寬胖”的不封閉橢圓形逐漸變成狹長的柳葉形，軸向塑性應變和能量耗散逐漸減小，但軸向塑性應變不斷累積；加載初期滯回曲線的加載段和卸載段都表現出較為明顯的非線性特征，同時加載段最大應力相位對應的動應變并不是最大的，最大應變而是出現在卸載段，說明出現應變滯后于應力現象。

4 回彈模量分析

土體回彈模量可反映其抵抗彈性變形能力，是評價變形和穩定性的一個重要指標，其定義為土體在動荷載作用下循環動偏應力與可恢復應變的比值，即：

式中，σdmax和σdmin分別表示某一滯回圈內的最大動應力和最小動應力；εdmax和εdmin分別表示某一滯回圈內的最大動應變和最小動應變。SEED 等[14]提出的計算方法適用于滯回圈閉合的情況，而加載初期試樣軸向塑性應變增加迅速，滯回圈不閉合。基于此，本文采用根據2個相鄰滯回圈確定回彈模量的方法[15]，圖8 為根據應力-應變關系曲線確定回彈模量的示意圖。振次N=5，6 的滯回圈沒有閉合，但是2 個滯回圈相交于點A，形成一個新的閉合滯回圈，端點為A和B(第5 個循環時滯回圈的底端點)，則振次N=5 的回彈模量值為A和B兩端點連線的斜率值。

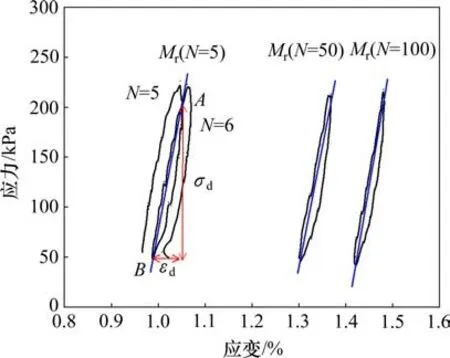
圖8 回彈模量確定方法Fig.8 Determination method of resilience modulus

圖9 為圍壓分別為30，60 和90 kPa 時，不同動應力下回彈模量與循環次數的關系。可以看出，粗粒土的回彈模量初期波動較大，其在加載初期的前10 個振次迅速減小，但這種減小趨勢很快結束。這是因為重塑試樣在初始剪切階段經壓實形成的結構受到一定程度的擾動，土體強度發生一定的衰減[16]。在循環荷載作用下，試樣中的顆粒會重新排列形成新的結構，試樣逐漸密實，表現出回彈模量緩慢增加。經歷加載初期的波動后，非飽和試樣的回彈模量呈現增加趨勢，即試樣的剛度隨循環次數的增加而逐漸硬化，和前文滯回圈向豎直方向發展的趨勢相對應。

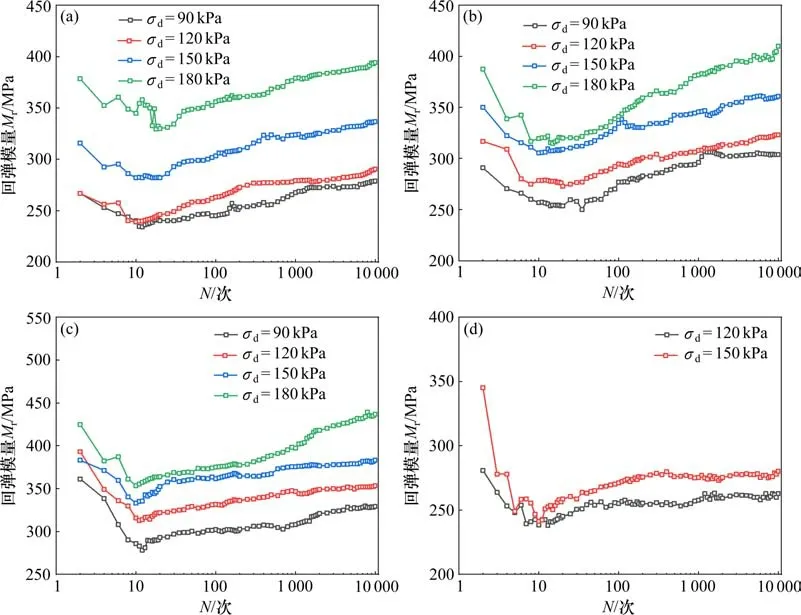
圖9 回彈模量Mr隨振次N的關系曲線Fig.9 Relationship between resilient modulus and cycle number

從圖9 可以看出，在相同的圍壓和含水率下，動應力越大，回彈模量越大，因為增大動應力，試樣壓密程度增加。為進一步分析回彈模量，計算最后1 000 振次回彈模量平均值，并將其作為回彈模量代表值。回彈模量代表值和動應力幅值的關系見圖10。由圖10 可知，圍壓和含水率的增加都對試樣回彈模量有著顯著影響。與非飽和試樣相比，飽和試樣中自由水含量增多，水分具有潤滑作用，形成的水膜可減小顆粒間摩擦力，因此無黏性粗顆粒更易滑動，使得試樣回彈模量衰減明顯。

圖10 回彈模量代表值和動應力的關系Fig.10 Relationship between representative value of resilient modulus and dynamic stress

5 累積塑性應變分析

5.1 累積塑性應變隨振次的變化規律

圖11 為試樣累積塑性應變εp與振動次數N的關系曲線。

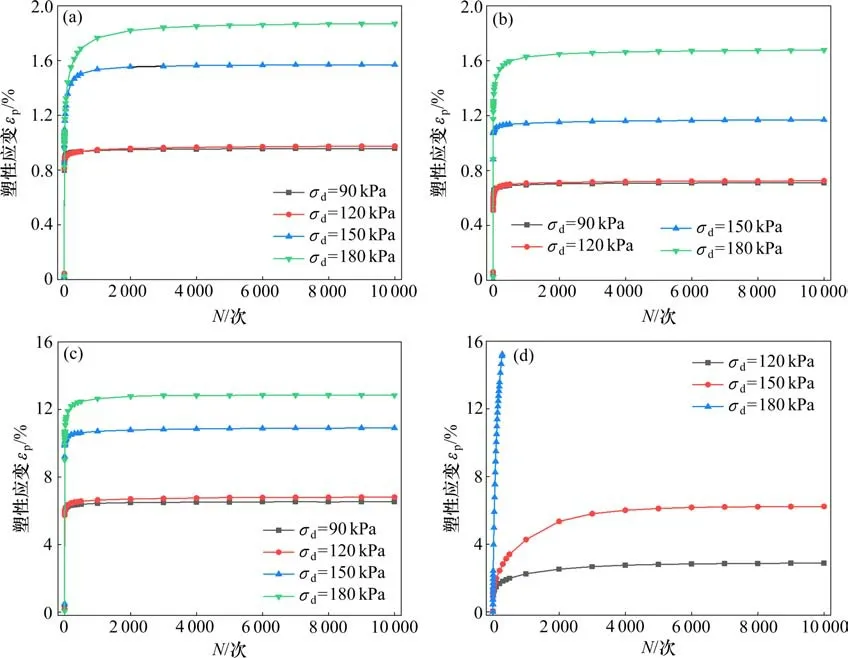
圖11 累積塑性應與振次的關系曲線Fig.11 Plastic strain accumulating with the number of load applications

由圖11 可知，非飽和試樣的動應力幅值較小時，試樣迅速壓密，動應力的增長對塑性應變的影響不顯著，而動應力增大到一定程度時，對塑性應變的影響會更明顯。循環荷載下顆粒材料的永久變形特性可采用安定理論描述[17-18]。非飽和試樣的塑性應變只在加載初期發展，隨著振次增加，塑性應變不再增加，試樣達到穩定狀態，且εp≤2%，軸向累積塑性應變值較小，基于安定理論將其劃分為塑性安定類型。動應力為120 kPa 和150 kPa 的飽和試樣塑性應變在加載后較快增加，隨后應變增加速率逐漸減小，到達穩定值，但其最終的累積塑性應變值較高，劃分為塑性蠕變類型；動應力為180 kPa 的飽和試樣塑性應變迅速發展，在振次N≤500范圍內εp達到破壞標準，劃分為增量破壞類型。動荷載作用下試樣內部顆粒發生滑移，重新排列，試樣迅速密實，且試樣所承受荷載的頻率比較低，一個振動循環所需時間長，試樣變形開展充分，造成前10 個振次內試樣累積塑性應變較大，李麗華等[19]采用相同的三軸儀器也得到類似的試驗結果。

5.2 圍壓的影響

為直觀分析圍壓和塑性應變間的關系，繪制圖12 的εp-σ3關系曲線。由圖12 可知，增大圍壓，試樣穩定性增加，塑性應變降低，且塑性應變與圍壓的關系曲線近似線性發展。粗粒土的累積變形產生機理和黏性土[20]完全不同。循環荷載下，顆粒不斷發生滑動、摩擦和轉動，且沿著最小做功面重排列，減小顆粒間摩擦力和嵌固的咬合力，導致土體產生剪脹變形。而圍壓增加，會增大試樣內部顆粒之間的咬合力和有效應力，從而增強試樣的抗剪強度，減小變形。

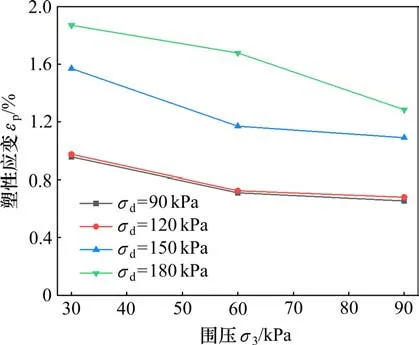
圖12 εp-σ3關系曲線Fig.12 Relationships between εp and σ3

5.3 含水率的影響

從圖13 可以看出，含水率對試樣塑性應變有明顯影響。當σd為120 kPa和150 kPa時，相比于非飽和試樣，飽和試樣的塑性應變分別增大了86.4%和160.9%；當σd為180 kPa 時，非飽和試樣塑性應變也很小，而飽和試樣迅速發生破壞，主要是因為循環荷載下飽和土體孔隙水壓力迅速上升，導致顆粒間有效應力降低。試驗結果說明含水率對塑性變形存在明顯影響，且動應力越大，影響程度越大。因此，在工程實踐中應及時排水，避免粗粒土填料的動力變形穩定性受到雨水影響而降低。

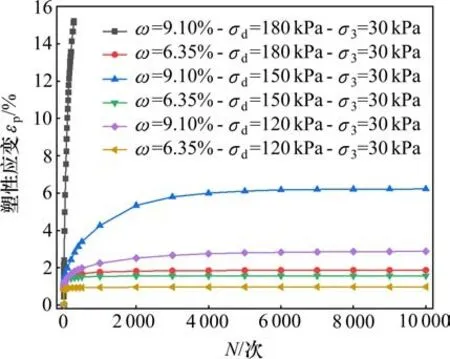
圖13 不同含水率下εp-N關系曲線Fig.13 Plastic strain accumulating with the number of load applications under different moisture content

5.4 塑性應變預測模型

車輛荷載的循環作用會引起路基的變形和不均勻沉降，而高速鐵路路基在一定軸次荷載作用下變形應趨于穩定，因此有必要對實際情況下承受運梁車荷載的路基填料塑性應變規律進行預測。目前，預測方程主要是建立在經驗和彈塑性模型基礎上。而彈塑性模型十分復雜，不適于實際工程分析。相比之下，經驗模型能反映塑性應變發展規律，常被學者用于工程實踐中。很多學者采用經典的指數模型[21]預測填料塑性應變規律。當振次不斷增大時，塑性應變也不斷增加，而室內試驗中試樣塑性應變最終趨于穩定值，因此，指數模型發展趨勢與實際情況不吻合，存在一定的缺陷[22]。

根據圖11 的曲線形態，本文采用雙曲線函數來描述最優含水率粗粒土試樣塑性應變εp與振次N的關系，擬合公式為：

式中：εp為塑性應變；N為荷載循環次數；α和β為雙曲線模型參數，當N趨于∞時，α為εp-N曲線漸近線，即最大塑性應變。

需要說明的是本文飽和試樣數量較少，擬合結果具有誤差，因此只對非飽和試樣結果進行擬合。式(2)對試驗數據的擬合效果較好，擬合相關系數R2基本大于0.90。根據前文分析，塑性應變值受圍壓σ3和動應力幅值σd影響顯著，因此參數α與以上因素密切相關。參數α在不同動應力下隨圍壓的變化曲線如圖14所示。

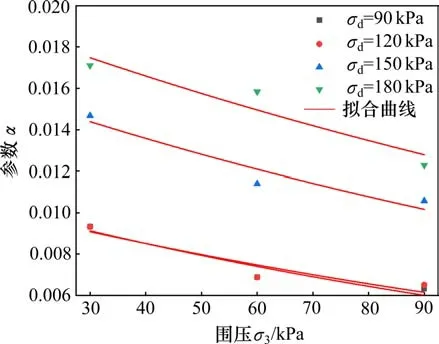
圖14 參數α與圍壓的關系曲線Fig.14 Relationships between α and confining pressure

由圖14 可知，指數函數可描述參數α與圍壓的關系，即

式中：a和b為擬合參數。利用式(3)擬合，分析發現參數a和b都與動應力呈現正相關關系。假定參數a與σd呈指數函數關系，b與σd呈線性函數關系，得到的關系式如下：

模型參數β可反映循環加載時塑性應變的變化規律，通常和土的類別、物理狀態相關，而靜三軸試驗的土體強度可間接代表土體物理狀態的影響[23]。因此，引入動靜應力比δ，即動偏應力σd和靜強度σs的比值。基于摩爾-庫倫破壞準則(式(6))，可推導出最優含水率試樣在圍壓為30，60，90 kPa時的靜強度值分別為337.67，424.23和510.79 kPa。

由圖15 可知，參數β隨動靜應力比的變化可以采用冪函數描述，即：

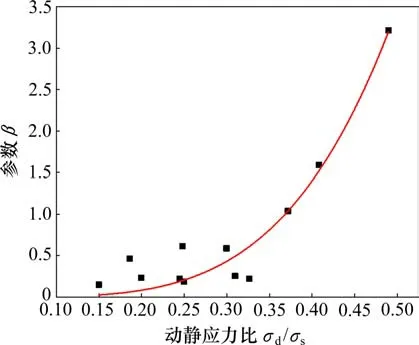
圖15 參數β與動靜應力比δ的關系曲線Fig.15 Relationships between β and δ

綜上可得：

基于式(8)，獲得了可綜合考慮圍壓、動應力以及荷載循環次數影響的累積塑性應變預測模型。

5.5 模型的驗證

為驗證塑性應變預測模型的合理性和適用性，利用文獻[5]中含水率為6%，加載頻率為1 Hz的試驗條件下粗粒土試樣的試驗結果進行驗證。采用式(8)計算文獻中應力狀態下粗粒土填料的塑性應變，并與試驗結果對比，如圖16 所示。隨振次的增加，預測值逐漸接近試驗值，說明累積塑性應變預測模型具有較高的準確度。當振次較小時，由于試樣級配、荷載頻率和試驗儀器的不同，預測值與試驗值存在一定差距，預測值發展較快，而試樣最終到達穩定狀態時，預測值稍大于試驗值，說明預測模型具有一定的準確性。

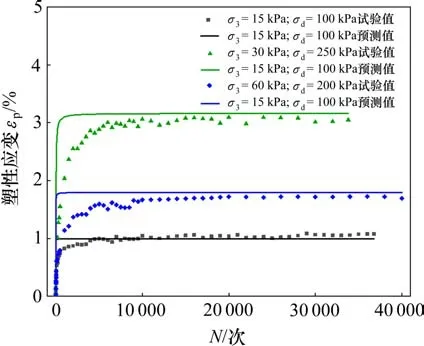
圖16 粗粒土填料累積應變結果對比Fig.16 Comparison of accumulative strain results of coarse-grained soil filler

6 結論

1) 加載初期粗粒土填料的回彈模量迅速減小，波動較大。隨著循環次數增加，飽和試樣回彈模量約在1 000 振次后趨于穩定，變化較小，非飽和試樣回彈模量仍不斷增加。

2) 粗粒土填料塑性應變受動應力水平、圍壓和含水率的影響明顯。動應力越大，塑性應變越大；圍壓越大，填料越穩定；非飽和試樣塑性應變值εp≤2%，都為塑性安定型，而飽和試樣塑性應變明顯增加，甚至發生破壞。因此，在路基工程中，應及時排水，避免粗粒土基床動力穩定性降低而導致運梁車荷載作用下路基發生失穩破壞。

3) 基于大型動三軸試驗結果，建立最優含水率下路基粗粒土填料塑性應變預測模型，預測結果可為后續路基的修整提供依據和參考。