基于POF傳感裝置的混凝土裂縫開度預測

戚 丹, 包騰飛, 趙 珍

(1.楊凌職業技術學院 水利工程學院, 陜西 楊凌 712100; 2.河海大學 水利水電學院, 江蘇 南京 210098)

1 前 言

內外環境的復雜性導致了水工混凝土結構中裂縫的產生具有不可預見性,裂縫擴展寬度是裂縫發展及壩體變形的重要參量,建立相應的裂縫開度預測模型,就能準確預測裂縫開度及其變化趨勢,判斷裂縫是否會發生失穩擴展,監控大壩結構是否安全。國外主要研究塑料光纖傳感器如何監測建筑物應變、位移等,在裂縫監測方面涉足較少;國內主要研究混凝土壩裂縫定量監測及POF布設和開裂條件下塑料光纖的力光轉換特性等[2-3],對基于POF傳感裝置的裂縫開展預測研究較少,本文將在以往研究不同光纖方位下光損耗值與裂縫開度的關系特性的基礎上,嘗試將不同光纖方位下光損耗值與裂縫開度關系進行量化,建立不同方位下裂縫開度預測模型,利用此預測模型由測量所得的光損耗值確定裂縫的擴展寬度,為后續進一步研究打下基礎。

2 多項式回歸預測模型

2.1 多項式回歸分析

回歸分析是一種傳統的統計方法,建立在對有相互關系的客觀事物大量試驗和觀察的基礎上,用來尋找聯系不確定的客觀現象之間的統計規律,即處理變量x與y之間關系的一種統計方法和技術[4]。回歸分析模型揭示事物間相關變量的數量關系,模型的建立涉及幾個重要步驟,如圖1所示。首先通過分析實際問題的目的設置因變量y,并選取影響y值的自變量x;其次進行這些變量數據的收集、整理,以便后期建立模型;然后尋找適當的數學形式來描述這些變量之間的關系(通過繪制散點圖來選擇數學模型,即將數據點繪制在坐標系中,根據這些點的分布狀況最接近哪種曲線就用相應的函數來描述);最后,在回歸模型建立之后,為了驗證這個模型是否準確,進行回歸模型的統計檢驗(包括擬合優度檢驗等)[5-6]。

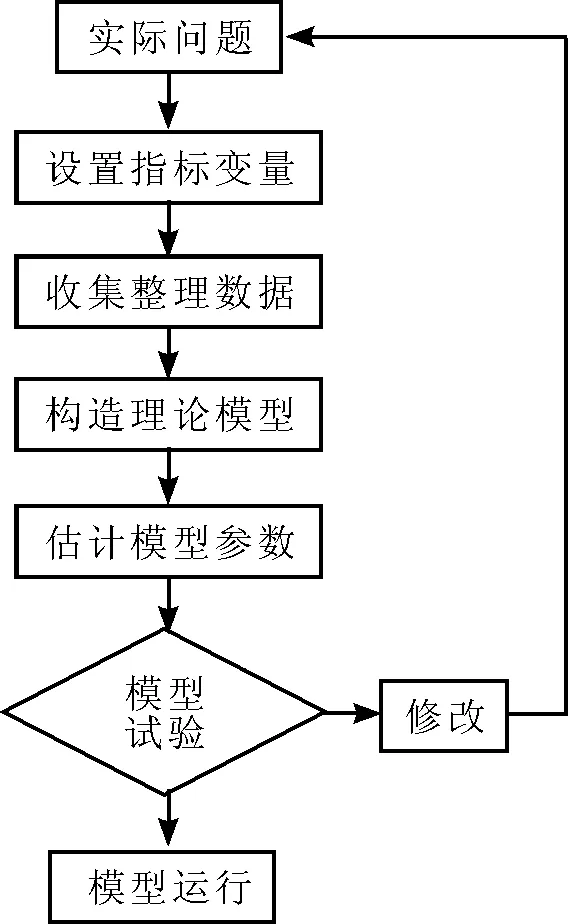
圖1 回歸模型建模步驟圖

多項式回歸分析是研究一個因變量與一個自變量或與多個自變量間的多項式關系的回歸分析方法,包括一元多項式回歸和多元多項式回歸。舉例如下:

一元n次多項式回歸方程:

yi=ao+a1x+a2x2+…+anxn+εa

(1)

二元二次多項式回歸方程:

(2)

式中:a0、b0為回歸常數;εa、εb為隨機誤差;al、a2、…、an以及b1、b2、…、b12稱為回歸系數。

當兩變量呈曲線關系時,需要用曲線方程式來擬合兩個變量的數學關系,設其中的因變量為y,自變量為x,則兩變量之間的關系可用式(2)來描述[7]。

2.2 裂縫開度預測模型

在已知不同光纖方位下裂縫開度與光損耗值對應數據的基礎上,以這些數據作為樣本,建立以光損耗值為自變量的裂縫開度預測模型。建立的裂縫開度預測模型涉及兩個變量,分別為光損耗值和裂縫開度,從所研究問題的目的出發,設置裂縫開度為因變量,光損耗值為自變量。由以往的研究[8]可知光損耗值與裂縫開度關系呈曲線變化趨勢,因此用式(2)來描述兩變量之間的關系。

然而當所建模型中自變量的最高次數小于等于3時,回歸系數容易解釋,回歸函數較穩定,回歸模型的應用不會受到影響。因而,冪次超過3的模型不常使用[1],本文嘗試建立二次多項式回歸模型和三次多項式回歸模型來預測裂縫開度,隨后通過試驗對比確定最優的多項式回歸預測模型。

綜上,建立二次多項式回歸模型和三次多項式回歸模型如式(3)、式(4)所示:

y=a0+a1x+a2x2

(3)

y=b0+b1x+b2x2+b3x3

(4)

式中:x為光損耗值;y為裂縫開度;a0、al、a2、a3以及b0、b1、b2、b3為回歸系數。

3 實例分析

3.1 試驗環節

由于塑料光纖傳感器僅停留在試驗研究階段,還未用于實際工程的裂縫監測,本次試驗將采用一種簡單的塑料光纖(Plastic optical fiber,簡稱為POF)裂縫傳感器裝置展開。該簡易POF裂縫傳感器如圖2所示,由三部分構成,分別為光源(功率為10 mW的紅光筆,發射光波長為650 nm,與塑料光纖工作波長一致且對人體不造成傷害)、光強度傳感介質(為三菱塑料光纖,包括與光源、光功率計連接的0.25 mm直徑塑料光纖尾纖和測裂縫的塑料光纖裸纖)以及光強度測量設備(型號JW3233的光功率計)。

圖2 塑料光纖裂縫傳感器簡易裝置圖

光源傳輸出來的光經過POF尾纖和POF裸纖后到達光功率計,POF裸纖因為外力作用發生彎曲變形時將出現光的外溢,使得到達光功率計的光的強度發生改變(變小)。圖3為本次試驗的裂縫模擬試驗示意圖。此時隨著活動玻璃板移動距離越遠(模擬建筑物裂縫擴展),光外溢越厲害,則光損耗越厲害。記錄活動玻璃移動之前的光強度值,再記錄活動玻璃移動時對應的光強度值,前者減去后者,可得到由于活動玻璃移動而產生的光強損耗值。重復以上工作便可通過POF裂縫傳感器簡易裝置和裂縫模擬裝置得到多組裂縫開度-光損耗值試驗實測數據。

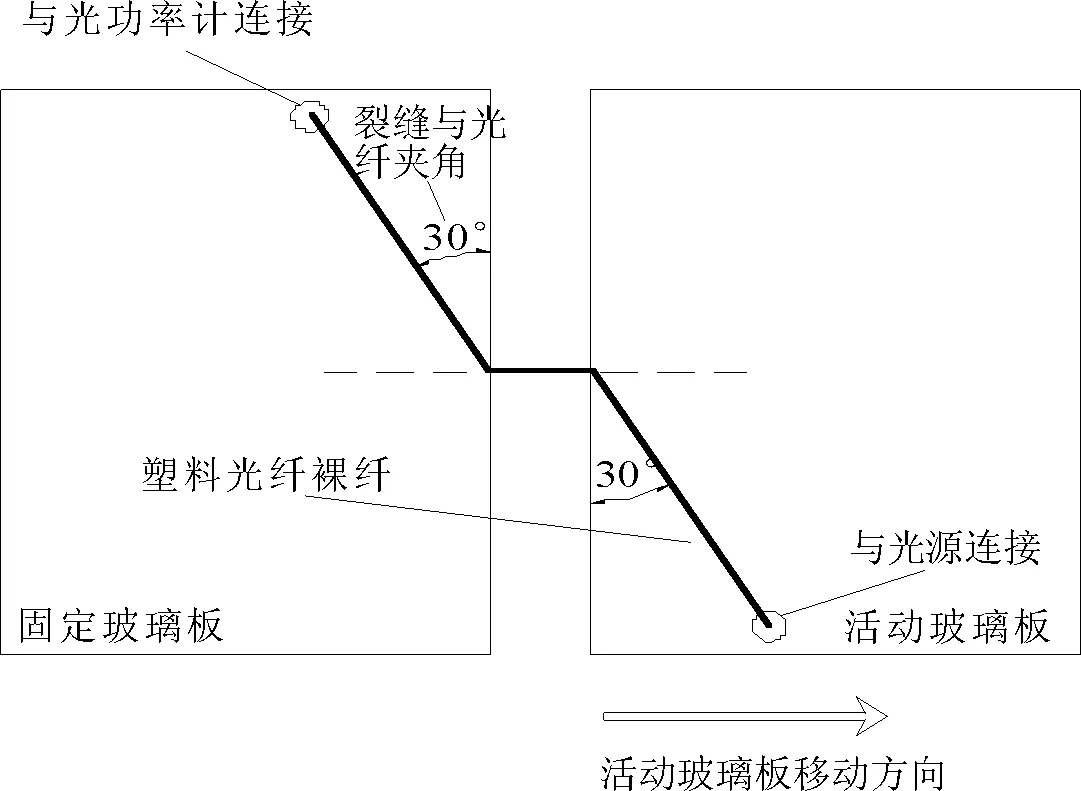
圖3 裂縫模擬試驗示意圖

借助于試驗設備,同時為了保證所建立模型的精度,增加試驗實測數據的樣本量,本次試驗將采用精度為0.1 mm的游標卡尺來測量裂縫開度。最終通過多組試驗,量測裂縫開度為0 mm、0.2 mm、0.4 mm、0.6 mm、……、5.8 mm、6 mm時的光損耗值,共計31組數據,如表1所示。其中,前21組數據用來建立預測模型,后10組數據用來驗證模型精度。

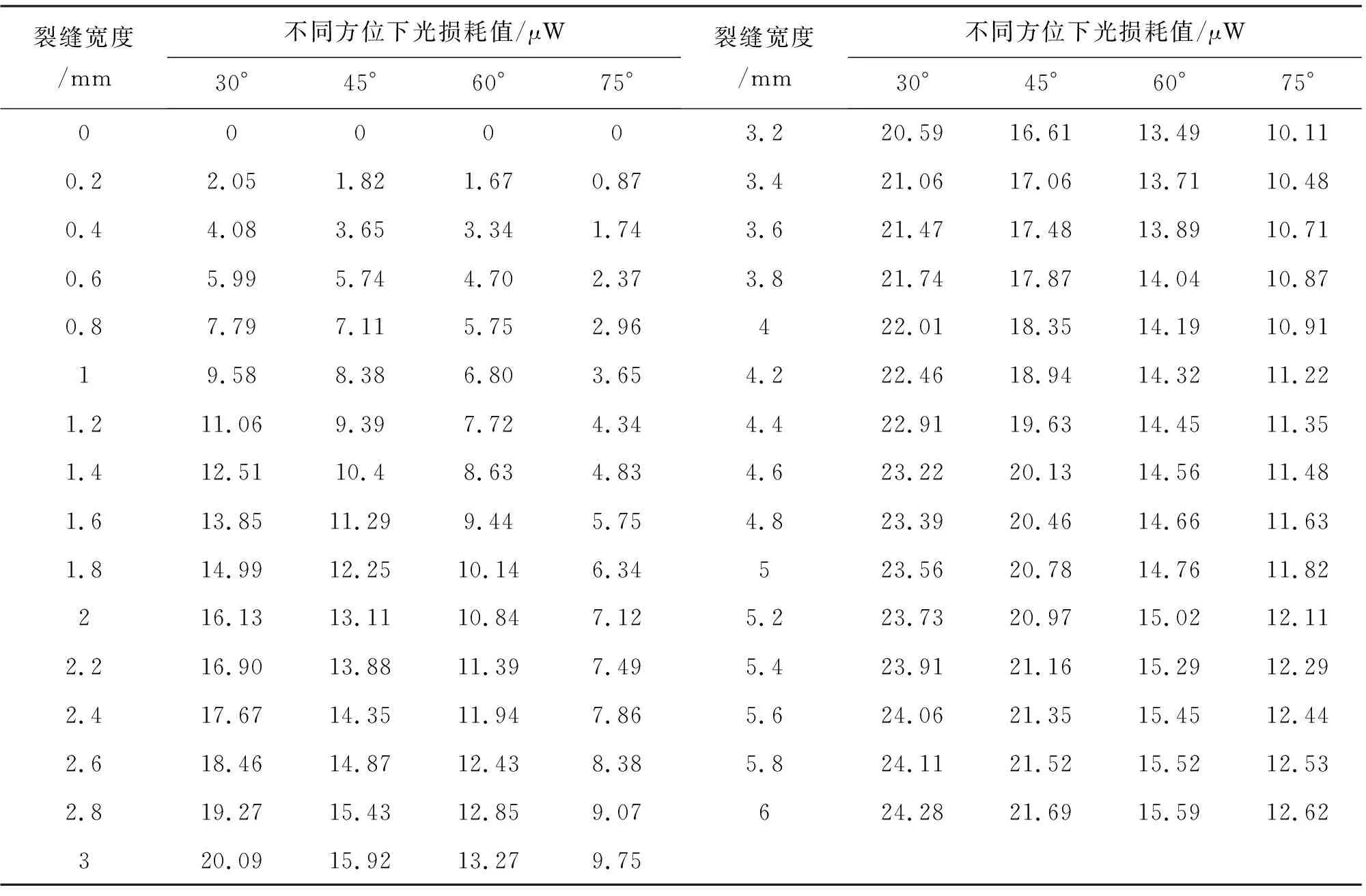
表1 試驗實測數據表

3.2 預測模型建立

以表1前21組數據(即0 mm、0.2 mm、……、3.8 mm、4 mm縫寬及對應光損耗值)作為樣本,結合式(3)和式(4),建立塑料光纖裂縫傳感器在方位角30°、45°、60°、75°下的二次多項式裂縫開度預測模型和三次多項式裂縫開度預測模型,分別如式(5)～式(8)及式(9)～式(12)所示,其中裂縫開度為因變量(單位:mm),光損耗值為自變量(單位:μW)。

(5)

(6)

(7)

(8)

(9)

(10)

(11)

(12)

實測裂縫開度-光損耗值關系曲線及二次多項式模型曲線和三次多項式模型曲線如圖4、圖5所示。

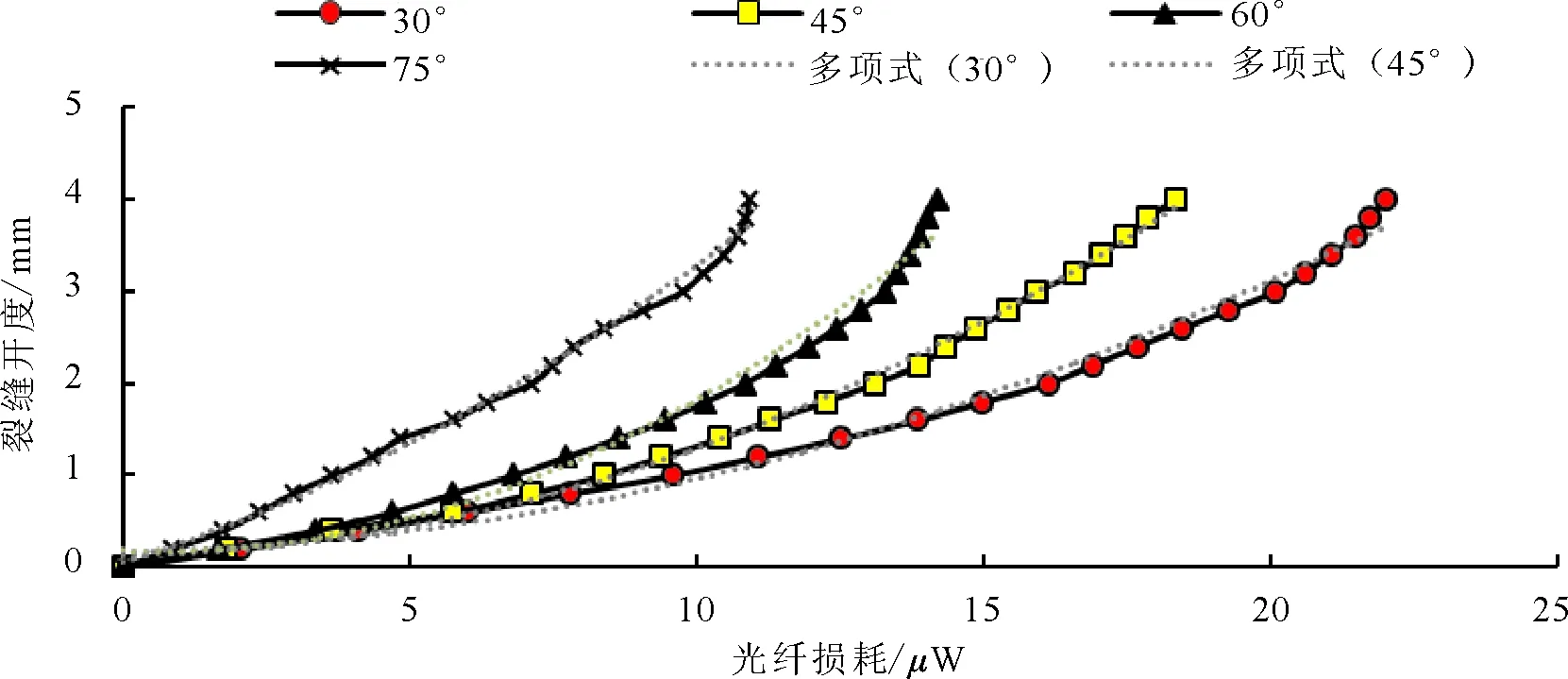
圖4 不同方位角下裂縫開度-光損耗值實測曲線及二次多項式預測曲線

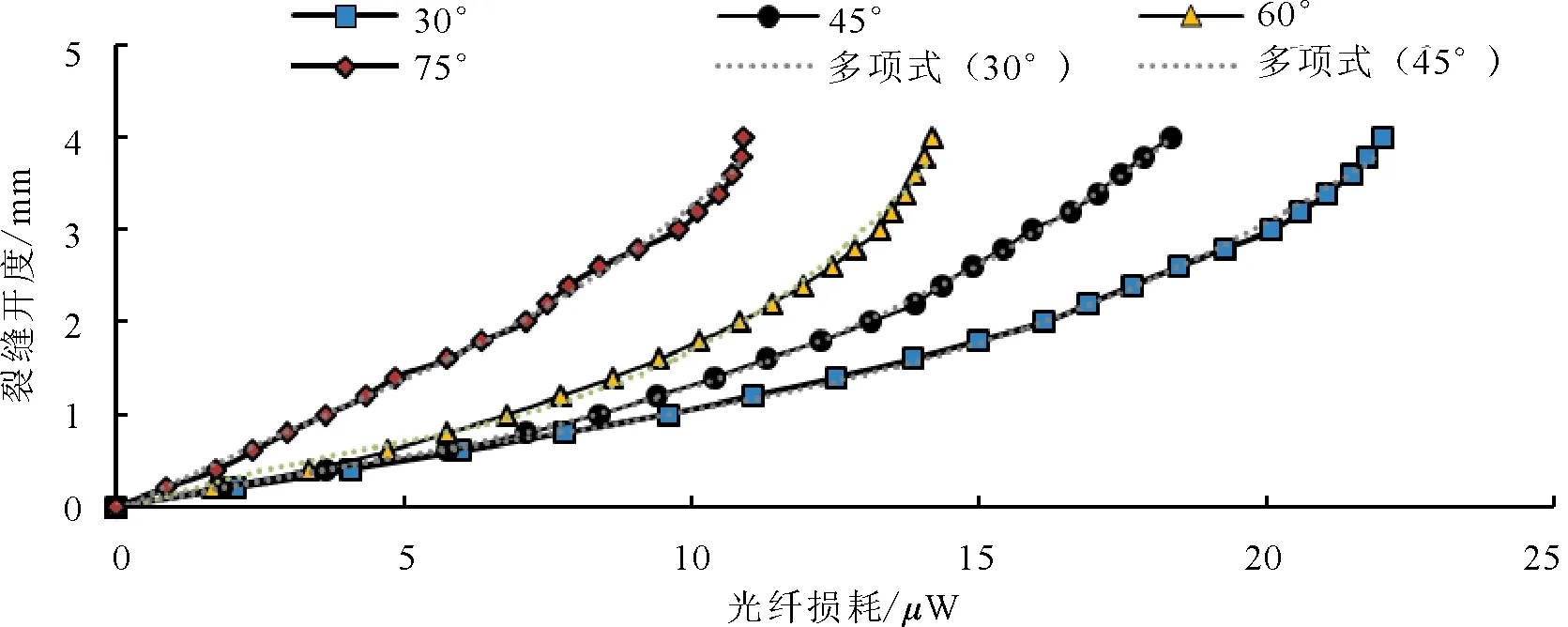
圖5 不同方位角下裂縫開度-光損耗值實測曲線及三次多項式預測曲線

所得的不同方位下的二次多項式預測模型回歸系數及樣本決定系數見表2,三次多項式預測模型相關參數見表3。

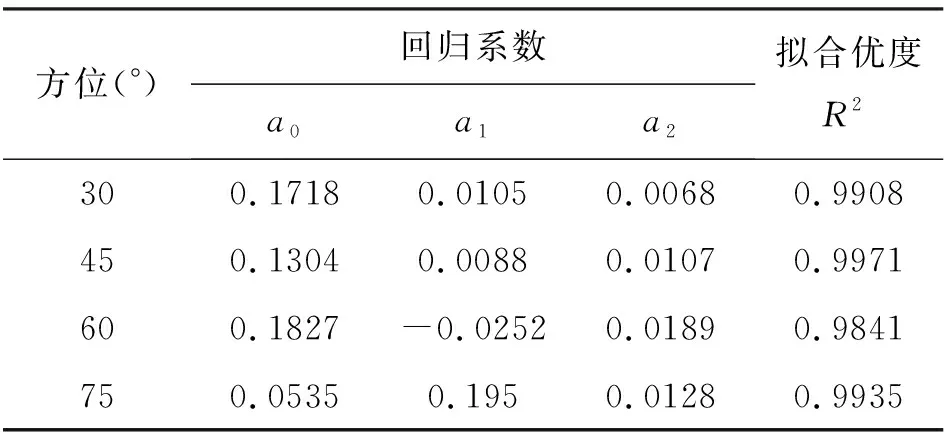
表2 不同方位下二次多項式回歸模型參數表

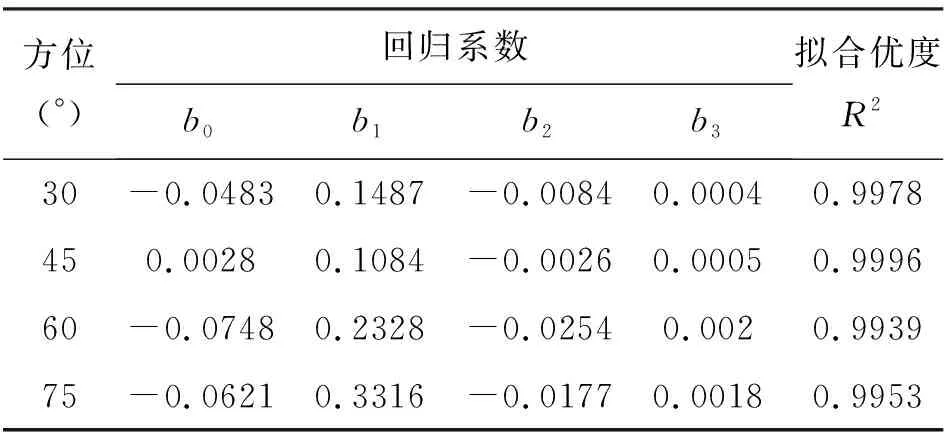
表3 不同方位下三次多項式回歸模型參數表

表中R2為擬合優度,又稱樣本決定系數,表示預測值與實測值擬合優度的相對指標。R2取值介于0到1之間,R2越小,擬合優度越差,反之,擬合優度越好。八個回歸模型的擬合優度R2全部大于0.984,且四個三次多項式回歸模型的擬合優度超過了0.993,可見所建的二次多項式回歸模型和三次多項式回歸模型均較成功,且三次多項式的擬合精度更高。

3.3 裂縫開度預測

參考表1,將不同方位下大于4 mm縫寬對應的光損耗值代入式(5)～式(12)中,可得裂縫開度預測值,如表4～表7所示。

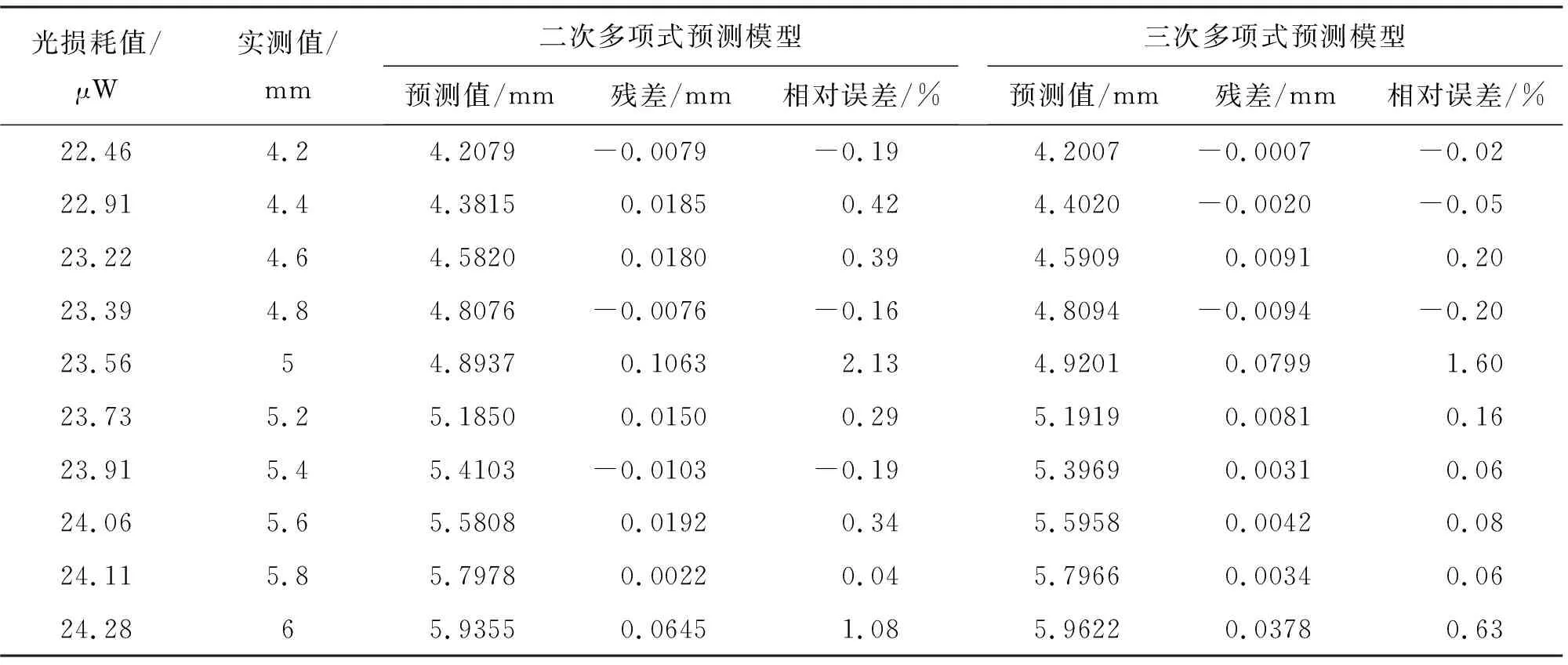
表4 30°方位角下裂縫開度預測值與實測值對比分析表

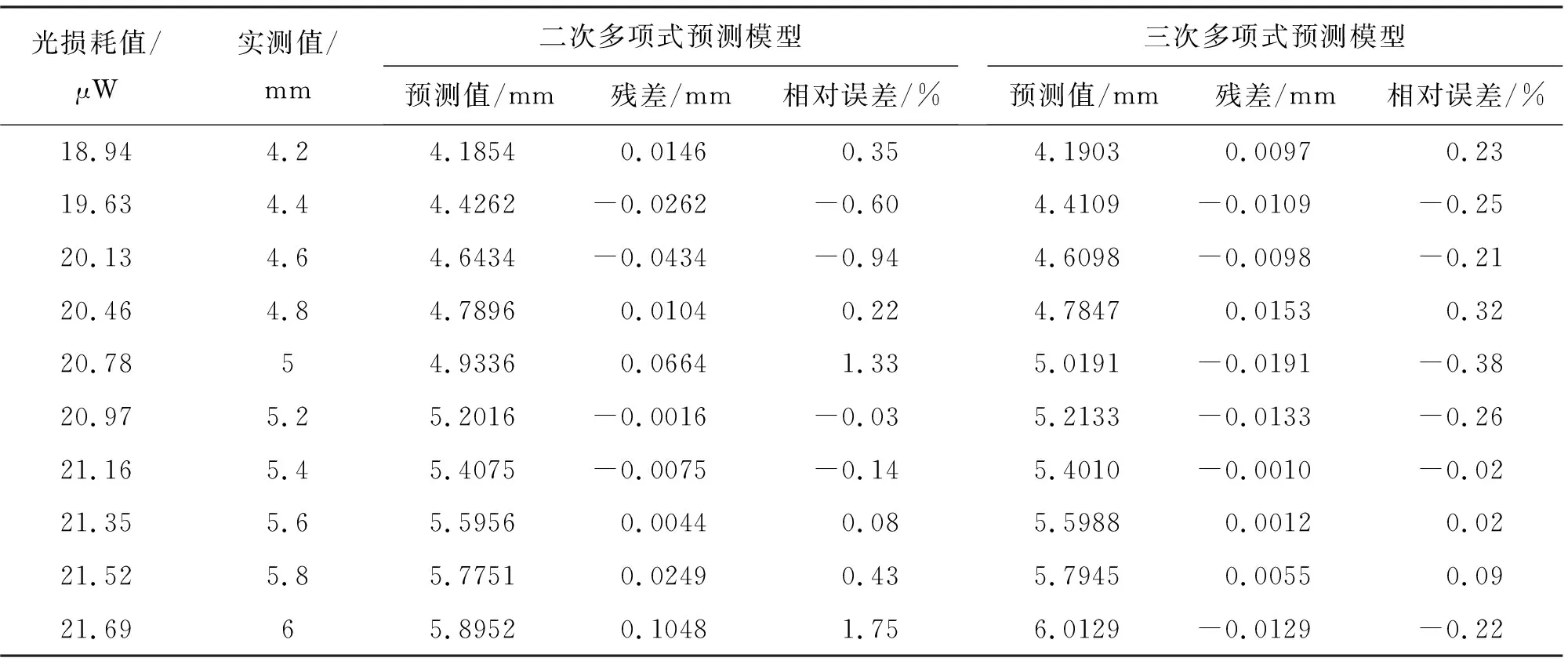
表5 45°方位角下裂縫開度預測值與實測值對比分析表

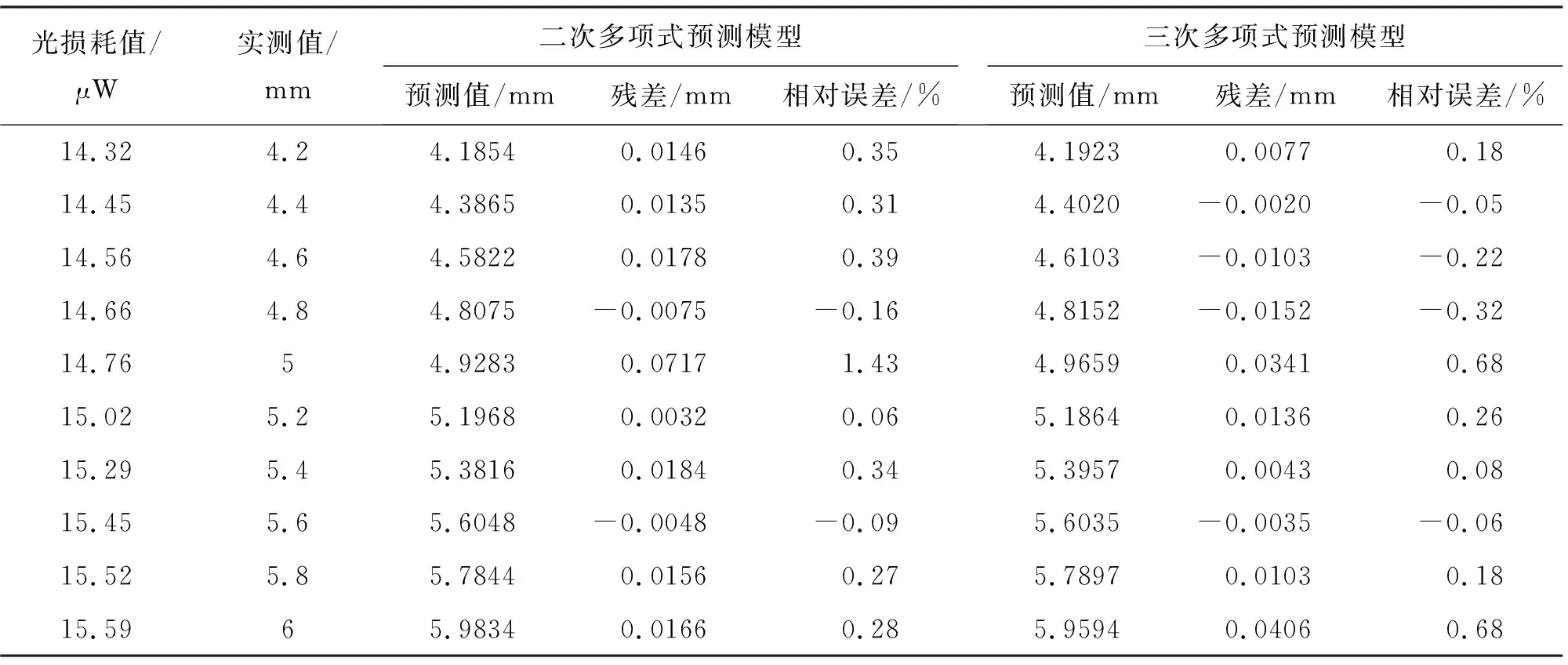
表6 60°方位角下裂縫開度預測值與實測值對比分析表

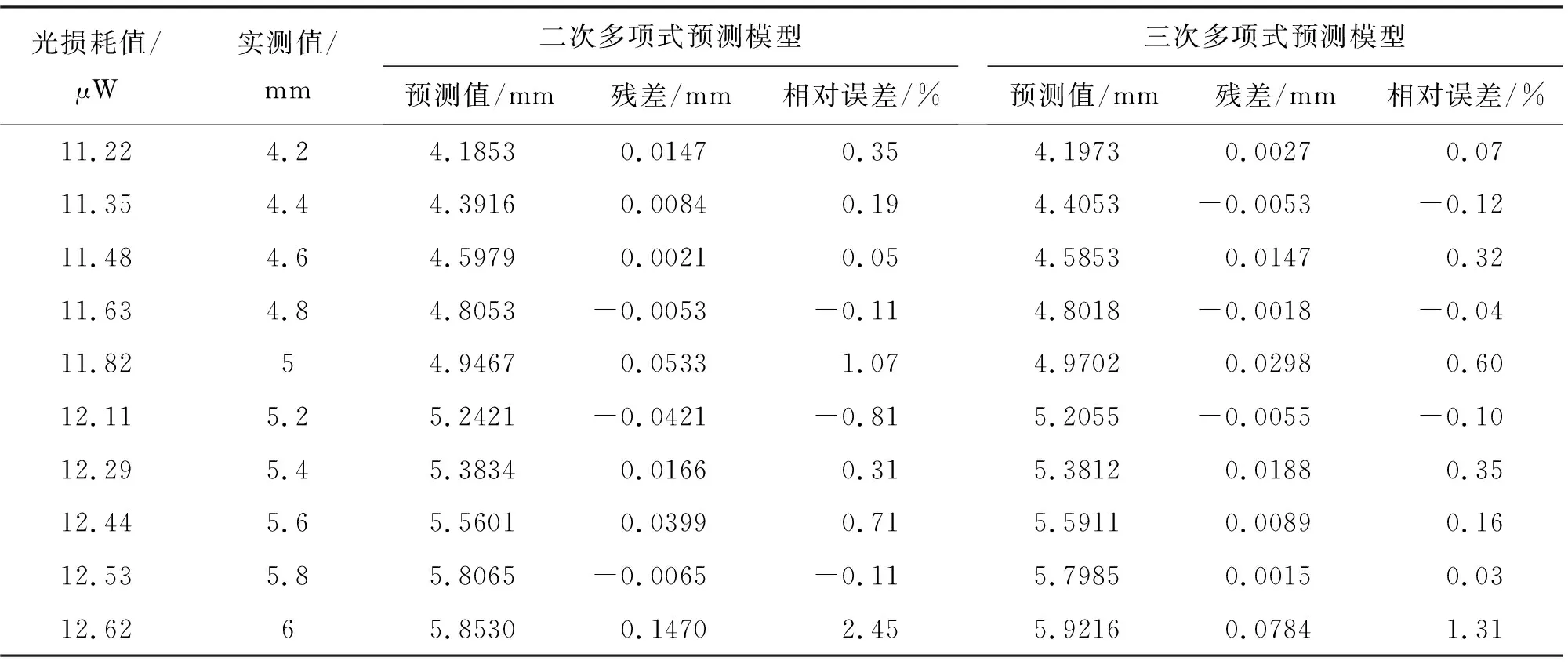
表7 75°方位角下裂縫開度預測值與實測值對比分析表

3.4 預測結果分析

由表4～表7可知,建立的八個裂縫開度預測模型的預測值相比于實測值,相對誤差值基本小于1.0%,塑料光纖在30°、45°、60°、75°方位角下的二次多項式預測模型殘差平方和分別為0.017、0.019、0.007、0.028,塑料光纖在30°、45°、60°、75°方位角下的三次多項式預測模型殘差平方和分別為0.008、0.001、0.004、0.008,最大相對誤差為0.92%,由此可知建立的八個預測模型均有較好的擬合精度,且三次多項式精度更高,這與3.2中的結論是一致的。

4 小結與展望

本文在介紹多項式回歸基本理論知識的基礎上,基于POF裂縫傳感器建立了不同方位下二次和三次多項式回歸裂縫開度預測模型,預測模型成功預測了裂縫的開展寬度,通過與實測數據的對比分析,驗證了預測模型在預測裂縫開度方面的可行性,兩種模型預測精度較高,且三次多項式模型精度更高。

但是,本文試驗研究均是建立在模擬裝置基礎上,在實際工程中會遇到其他不可知的影響因素,因此所見模型的精度還需要結合實際工程進行進一步的研究和驗證。