不同基準年級下錨題難度范圍與年級離散程度對垂直量尺化的影響*

黎光明 張曉婷

(華南師范大學心理學院,心理應用研究中心,廣州 510631)

1 引言

垂直量尺化(vertical scaling),又名垂直量表化、垂直等值(vertical equating),是指在某個特質領域內,在縱向發展的不同水平(如年齡、年級)群體之間,建立關于群體或者個體特質水平發展狀況的評價參照體系的過程(漆書青,戴海崎,1992)。垂直量尺化廣泛應用于TIMSS、PISA等國際大型測驗(羅照盛,2012;Kolen &Brennan,2013)。當不同測驗之間的難度水平相差較大且受測者的能力水平存在一定差距時,不再滿足測驗等值(testing equating)中的水平等值(horizontal equating)條件,宜使用垂直量尺化,其能夠有效評價和預估個體或群體動態發展水平和趨勢,進而為教育發展與評估提供相關建議。

垂直量尺化主要是用來描述某一群體的縱向發展水平,而水平等值需要建立各個平行測驗之間的確切關系,相較而言,垂直量尺化的流程無需進行最后的測驗等值步驟,卻需將非平行測驗轉換到同一量尺(葉昶成,2015)。對于能力不同層次的測驗群體,比如小學1～4年級學生,必須選定一個年級作為分數轉化的基準,將其他年級的分數轉化到該年級上形成一個統一分數量尺,一般稱為垂直量尺(vertical scale)或發展性量尺(developmental scale)。由于分數轉化的算法是一個逐步疊加的過程,比如從3年級轉化到2年級再轉化到作為基準的1年級,所以當前年級距離基準年級越遠,轉化的次數越多,受到等值方法誤差的影響可能就越大,垂直量尺化精度可能就越低(郭小軍,2014;梁正妍,2017)。因此,在實踐中通常選用處于中間的年級作為基準來減少誤差。

在構建垂直量尺的最初階段,需要選定相應模型擬合被試的真實作答情況,針對二級計分的測驗,通常會選擇邏輯斯蒂克模型(Petersen et al.,1989)。郭小軍(2014)采用兩參數logistic模型(2PLM)進行數據模擬,發現基準年級的選取和年級離散程度對垂直量尺化效果產生較大影響。梁正妍(2017)同樣采用2PLM,探究年級離散程度與錨題比例對于垂直量尺化的影響,發現兩者存在交互作用。

錨題的代表性對測驗等值的影響一直以來受到眾多研究者關注,其中典型的有錨題難度范圍的代表性(葉萌,辛濤,2015)。葉萌和辛濤(2015)對垂直量尺化中錨題代表性問題進行了詳細的闡述,提出了錨題難度范圍的設定會影響垂直量尺化的精度,其將垂直量尺化中錨題難度范圍設置為三種水平,結果發現不同錨題難度范圍對垂直量尺化性能和參數返真都有影響,但其沒有在不同年級離散程度的群體中進行探討,未能發現年級離散程度和基準年級的設置對錨題難度范圍選取的影響。在錨題設計中,如何選取難度合適的題目構成錨題是實踐中的關鍵問題和難點。由于錨題處于低年級測驗的結尾和高年級測驗的開始位置,如果錨題選取不當,則會出現項目參數漂移(item parameter drift),即同樣的題目在兩個位置發揮不同的作用,從而降低垂直量尺化的精度(Wells et al.,2002)。過往的研究和實踐中錨題是從低年級測驗中隨機抽取的,不能保證難度的代表性。對于如何設置錨題難度范圍這一問題,Sinharay和Holland(2006,2007)研究發現,在題目難度和測驗特征的關系中沒有表明微型錨測驗(錨題與總測驗難度范圍相匹配)是理想的錨測驗,其設置了三種難度范圍的錨測驗,分別是微型錨測驗、midi錨測驗(在內容上對總測驗具有代表性,但只包括中等難度的題目)以及半midi測驗(難度范圍小于微型測驗,但大于midi測驗),結果顯示midi錨測驗和總測驗的相關穩定性高于微型錨測驗和總測驗的相關穩定性,midi錨的性能和微型錨的性能一樣,后續的研究也驗證了這一結論(Liu et al.,2011)。Chin等(2006)在垂直量尺化中將錨題難度范圍設定為小中大三個等級,結果發現不同錨題難度范圍對垂直量尺化性能和參數返真都有影響,難度范圍擴大會使這兩種分析結果更準確。可見,在實際應用中設置錨題難度范圍的標準是十分重要的。

前人對于垂直量尺化影響因素的研究較為深入,分別從被試數量、題目數量、年級數量、基準年級、年級離散程度、錨題比例、難度范圍等方面對垂直量尺化的影響進行了較為深入的探討。但是,前人的相關研究仍然存在以下問題:一是多采用兩參數logistic模型(2PLM)來估計項目參數和能力參數,未能估計猜測參數c,實際上,相比2PLM,三參數logistic模型(3PLM)更加適用于可猜測作答的選擇題等客觀題型(戴海琦,張峰,2018),使用范圍增大,可能將提高垂直量尺化的精確性;二是對于錨題的代表性研究,未能同時關注“錨題難度范圍”和“基準年級選取”,缺乏探討對于不同基準年級下錨題難度范圍與年級離散程度對垂直量尺化的影響,這對于錨題設計下的垂直量尺化研究來說,是可以深入分析的方向。

基于此,本文對錨題的選取提出了更高的要求,以不同錨題難度范圍和不同基準年級“聯合作用”為突破點,使用3PLM,探討不同基準年級下錨題難度范圍與年級離散程度對垂直量尺化的影響。

2 方法

2.1 研究設計

采用2×3×3三因素隨機實驗設計,自變量1為基準年級(邊緣年級,中間年級);自變量2為錨題難度范圍(較小[μlow,μhigh]、中等[μlow-σ,μhigh+σ]、較大[μlow-2σ,μhigh+2σ]);自變量3為年級離散程度(相鄰年級間效應ES大小:0.5、1.0、1.5)。因變量為等值精度指標Bias和RMSE(Briggs &Peck,2015;Briggs &Dadey,2015)。

(1)基準年級。對于基準年級的選擇一般有兩種,即邊緣年級(低年級或高年級)和中間年級。本文設定了四個年級,對于基準年級,邊緣年級為1年級,中間年級為2年級。采用非等組錨題設計,錨題為相鄰年級共用的題目。

(2)錨題難度范圍。依據Chin等(2006)選取標準,分別選取錨題難度范圍較小(兩個相鄰年級能力均值之間),錨題難度范圍中等(低于低年級群體能力均值一個標準差和高于高年級群體能力均值一個標準差之間),錨題難度范圍較大(低于低年級群體能力均值兩個標準差和高于高年級群體能力均值兩個標準差之間),作為錨題難度范圍的指標。

(3)年級離散程度。垂直量尺化的結果一般從三個角度進行評價,即跨年級增長(grade-to-grade growth)、跨年級變異(grade-to-grade variability),以及年級間的離散程度(separation of grade distribution)。其中,年級間的離散程度應用最為廣泛,是指兩個相鄰年級的量尺分數分布的重疊程度,俗稱為“年級離散程度”。多數研究使用效應大小(Effect Size,ES)這一統計量來表示年級離散程度(Yen,1986),其計算公式為:

(1)

(4)固定變量。蔡艷等(2009)通過固定被試數和測驗長度,得出當測驗長度為100時錨題比例最低可達14.29%。熊建華等(2010)提出當測驗長度為600、300、200、100題時,相應比例可以降低到1/15、1/12、1/10、1/5。參考前人研究,本文錨題比例固定為20%。題目數固定為100,年級人數固定為1000。

2.2 模擬流程

分別以低年級和中間年級作為參照基準,使用自編R3.0程序,基于蒙特卡洛模擬法,采用三參數logistic模型獲得四個不同年級組被試在本年級上的作答矩陣。模擬四個年級上各100道題目的項目參數以及各年級1000名被試的能力參數。使用BILOG-MG軟件進行同時估計(Yildirim,2014),計算不同錨題難度范圍以及不同年級離散程度下4個年級的偏差Bias和返真性參數RMSE。

以低年級為基準年級為例,具體模擬過程見圖1。

圖1 基準年級為低年級時模擬流程圖

2.3 評價指標

常用的垂直量尺化評價指標為Bias和RMSE。

(1)Bias,即平均偏差,是考察真值與估計值之間偏差的一個指標,其主要用于檢測研究中是否含有系統誤差,以及偏差的方向性問題。Bias值為正,代表低估,Bias值為負,代表高估。

(2)

(2)RMSE,即均方根誤差(Root Mean Square Error),是真值與觀測值偏差的平方和觀測次數n比值的平方根。均方根誤差對一組測量中的特大或特小誤差反映非常敏感,所以能夠很好地反映出估計的精度。RMSE是對一組測量數據可靠性的估計。RMSE越小,測量的可靠性越大,估計精度就越高。

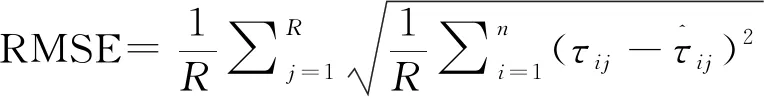
(3)

3 結果

3.1 各條件下Bias結果

圖2和圖3為各條件下項目參數、被試能力參數Bias折線圖。

圖2 基準年級為低年級時不同條件下各年級項目與能力參數Bias值折線圖

圖3 基準年級為中間年級時不同條件下各年級項目與能力參數Bias值折線圖

由圖2a～圖2d可知,基準年級為低年級時,對于各年級項目參數而言,會出現普遍高估的情況,對于被試能力參數來說,會出現普遍低估的情況。隨著與基準年級距離的逐漸增大,各參數的估計精度也逐漸下降,且在年級4上的表現尤為明顯。究其因,是由于錨題設計下垂直量尺化通過等值公式進行累加轉換,離基準年級越遠,轉換的次數就越多,其估計的誤差就越大。由此可知,錨題設計下垂直量尺化的轉換不宜超過兩個年級,此結果與郭小軍(2014)的研究結果相似。

由圖3a～圖3d可知,基準年級為中間年級時,對于區分度參數a和被試能力參數θ而言,其Bias值時正時負,說明對參數的估計會出現忽高忽低的情況。對于難度參數b和猜測度參數c則傾向于高估,這種情況可能與基準年級的改變有關。與此同時,以中間年級為基準年級時,除區分度參數外,對其他參數的估計,年級1產生的Bias值始終大于年級3。這兩個年級的錨題均從年級2上選取,在垂直量尺化過程中的轉換次數也相同,唯一區別在于:對于年級1來說,其錨題是從比自身高的年級上選取的,對于年級3來說,其錨題是從比自身低的年級上選取的。因此,根據Bias結果,這表明在垂直量尺化中,從高年級選取錨題會比從低年級選取錨題產生更大誤差。

綜合圖2和圖3,對比發現,基準年級為中間年級時,各參數的Bias的絕對值明顯小于基準年級為低年級時,說明以中間年級為基準進行的垂直量尺化,將會產生更小的估計誤差。

3.2 各條件下RMSE結果

圖4和圖5為各條件下項目參數、被試能力參數RMSE折線圖。

圖4 基準年級為低年級時不同條件下各年級項目與能力參數RMSE值折線圖

圖5 基準年級為中間年級時不同條件下各年級項目與能力參數RMSE值折線圖

基準年級為低年級時,對于區分度參數a(圖4a),年級離散程度為0.5和1.0時參數估計精度差別不大,且均好于年級離散程度為1.5。對于猜測度參數c(圖4c),三種年級離散程度下的參數估計精度相差不大。然而,對于難度參數b(圖4b)和被試能力參數θ(圖4d),均當離散程度為0.5時,估計精度最好;年級離散程度為1.0和1.5時,在個別情況下均存在較大誤差。因此,綜合看來,在基準年級為低年級時,對于所有參數,年級離散程度為0.5時估計精度最好,年級離散程度為1.0時次之,年級離散程度為1.5時最差。

在基準年級為低年級時,對于區分度參數a(圖4a),中等或較大錨題難度范圍下的估計精度較好,較小難度范圍下估計精度最差。對于難度參數b(圖4b),較大錨題難度范圍下的估計精度較好,中等范圍次之,較小難度范圍下估計精度最差。對于猜測度參數c(圖4c),較小或較大難度范圍下的估計精度較好,中等范圍次之,但總體來說三種錨題難度范圍下的猜測度參數估計結果相差不大。對于被試能力參數θ(圖4d),中等或較大難度范圍下的估計精度較好,較小范圍次之。因此,綜合看來,在基準年級為低年級時,較大難度范圍下的參數估計精度最佳,參數返真性最好,中等范圍次之,較小范圍最差。

在基準年級為低年級時,對于區分度參數a(圖4a),年級離散程度為0.5時,對于年級1、2,較大錨題難度范圍下的結果最佳,對于年級3,中等范圍最好,對于年級4,較小范圍最好。年級離散程度為1.0時,對于年級1、2、3,中等錨題難度范圍下的效果最好,對年級4較大范圍最好。年級離散程度為1.5時,只有較小錨題難度范圍下的結果收斂。對于難度參數b(圖4b),年級離散程度為0.5時,在各年級上,三種錨題難度范圍下的結果差別不大。年級離散程度為1.0時,年級1、2、3在較大錨題難度范圍下表現最好,年級4在較小錨題難度范圍下表現最好。年級離散程度為1.5時,只有較小難度范圍下的結果收斂。對于猜測度參數c(圖4c),在各年級離散程度與錨題難度范圍下,4個年級結果差別不大。對于被試能力參數θ(圖4d),年級離散程度為0.5時,三種錨題難度范圍下被試表現差別不大。年級離散程度為1.0時,在中等和較大錨題難度范圍下,4個年級表現均較好,較小方范圍產生的誤差最大。年級離散程度為1.5時,只有較小錨題難度范圍下的結果收斂。

基準年級為中間年級時,對于區分度參數a(圖5a),當年級離散程度為0.5時,估計精度最好;當年級離散程度為1.0時次之,而當年級離散程度為1.5時,結果不夠穩定,在各個年級上起伏較大。對于難度參數b(圖5b),當年級離散程度為0.5和1.0時,估計精度均較好;而當年級離散程度為1.5時,結果不夠穩定,在各個年級上起伏較大。對于猜測度參數c(圖5c),年級離散程度為0.5和1.0時參數估計精度差別不大,且均好于年級離散程度為1.5時參數估計的精度。對于被試能力參數θ(圖5d),當年級離散程度為0.5時,估計精度最好;當年級離散程度為1.0時個別條件下誤差較大;當年級離散程度為1.5時,估計精度不如其他兩種情況。因此,綜合看來,在基準年級為中間年級時,年級離散程度為0.5時估計精度最好,年級離散程度為1.0時次之,年級離散程度為1.5時最差。

在基準年級為中間年級時,對于區分度參數a(圖5a),中等或較大難度范圍下估計精度較好,較小錨題難度范圍下估計的誤差不穩定。對于難度參數b(圖5b),中等難度范圍下估計精度較好,較大范圍次之,較小難度范圍下估計精度最差。對于猜測度參數c(圖5c),中等及較大難度范圍下估計精度較好,較小范圍次之。對于被試能力參數θ(圖5d),中等難度范圍下的估計精度較好,較小或較大難度范圍下的估計結果均在個別條件下存在較大誤差。因此,綜合看來,在基準年級為中間年級時,中等難度范圍下的參數估計精度最佳,參數返真性最好,較大范圍次之,較小范圍最差。

在基準年級為中間年級時,對于區分度參數a(圖5a),年級離散程度為0.5時,對于年級1、2、3,較大錨題難度范圍下的結果最佳,對于年級4,較小范圍最好。在年級離散程度為1.0時,對于各年級,較小難度范圍下的效果最好,但中等難度范圍下的效果與之差別不大。在年級離散程度為1.5時,對于各年級,中等難度范圍下的效果最好。對于難度參數b(圖5b),年級離散程度為0.5和1.0時,各年級在三種的估計結果差別不大。在年級離散程度為1.5時,對于各年級,中等難度范圍下的結果最好。對于猜測度參數c(圖5c),年級離散程度為0.5和1.0時,對于各年級,三種錨題難度范圍下的誤差均較小。在年級離散程度為1.5時,對于各年級,中等或較大錨題難度范圍下的結果均較好。對于被試能力參數θ(圖5d),年級離散程度為0.5時,各年級在三種錨題難度范圍下的被試表現差別不大。在年級離散程度為1.0和1.5時,各年級在中等錨題難度范圍下的表現最好。

綜合圖4和圖5,對比發現,當基準年級為中間年級時,RMSE整體誤差小于基準年級為低年級時產生的誤差。

4 分析與討論

4.1 不同基準年級對垂直量尺化參數估計的影響

當基準年級為中間年級時,Bias和RMSE的整體誤差均小于基準年級為低年級時產生的誤差。這表明,基準年級的選擇會影響垂直量尺化的結果。錨題設計下的垂直量尺化過程是一個累加轉換的過程,換言之,由于只有相鄰年級間存在錨題,因而與基準年級較遠的年級需要經過層層轉換,最終轉換到基準年級上,而多次的轉換勢必造成偏差的累加,正因為存在這種“累積效應”,所以通常需要選擇中間年級作為基準年級(Yen et al.,2012)。

當基準年級為中間年級時,到高年級和低年級的垂直量尺轉化是方便的。如果選擇以低年級或高年級作為基準年級,則有可能加大垂直量尺轉化難度,顯得“路途遙遠”,而以基準年級選擇為中間年級,顯得更為方便。因此,在教育與心理實踐中,為了更加關注學生的連續發展和學業上的進步模式,或為了更加關注學生在不同學年的進步表現,年級與年級之間的垂直量尺轉化選擇以“中間模式”較好,以防止垂直量尺化過程中產生更大的誤差。

4.2 與基準年級的間隔對垂直量尺化參數估計的影響

整體而言,當年級離散程度為0.5時,估計精度最好,且隨著年級離散程度的增大,估計精度隨之下降。當年級離散程度為1.5時,估計精度極不穩定,甚至出現了數據無法收斂的情況。特別地,即使以中間年級作為基準年級,雖然沒有出現類似以低年級為基準年級時無法收斂的情形,但在年級4上也出現了一些極不穩定的Bias和RMSE值,特別是在難度參數和能力參數上,形成若干Bias和RMSE“極端值”。

基于非等組錨題設計,以低年級為基準年級時,在Bias和RMSE上,出現較多的無法收斂的情況,其原因是由于年級離散程度過大,年級與年級之間的“異質性”增加,不同年級學生的“能力差異”就會不斷放大,造成“分數偏差”增加,最終導致難以相互轉化(Ye &Xin,2014)。同樣地,以中間年級為基準年級時,雖然情況有一定的好轉,但也出現了較多的偏差“極值”。如果轉換超過兩個年級,那么垂直量尺化精度開始下降。特別地,在年級4上出現了若干Bias和RMSE“極值”。基于此,在教育與心理實踐中,如追蹤監測學生的學業進展,進行垂直量尺化時,建議與基準年級間隔不宜超過2個年級。

4.3 不同年級離散程度下的參數估計分析

年級離散程度為0.5時,垂直量尺化精度最好,年級離散程度為1.0時次之,年級離散程度為1.5時,垂直量尺化精度最差。在3PLM下,不同基準年級下,年級離散程度越小,估計精度越好,這與前人使用2PLM得出的結果是一致的(梁正妍,2017;郭小軍,2014)。年級離散程度越大,對于距離基準年級越遠的年級,垂直量尺化精度越低。因此,在實際的教育與心理測量實踐中,年級離散程度不宜過大,否則會影響垂直量尺化的精度。

實際上,在使用項目反應理論方法進行垂直量尺化時,需要滿足兩大潛在假設:一是年級內的測驗單維性(Unidimensionality);二是年級間測驗同構性(Construct invariance)(Li,2011;Martineau,2004)。單維性是指每道題目只測量單一的潛在能力特質;同構性是指不同年級水平或難度水平的測驗維持相同的內容結構(Li &Lissitz,2012;Reckase &Martineau,2004)。在垂直量尺化實踐中,普遍涉及到3～6個年級的多組學生和試題。在試題層面,所考察的知識點跨度較大,因此跨年級同構性假設一般較難滿足。Martineau(2006)最初用結構漂移(Construct shift)一詞來描述違背同構性假設的現象。以數學測驗為例,在進行垂直量尺化時,3年級題目和6年級題目雖然都是考察數學知識,但是具體考察的知識點可能是很不一樣的。

4.4 不同錨題難度范圍下的參數估計分析

隨著與基準年級距離的逐漸增大,各參數的估計精度也逐漸下降,在年級4上表現尤為明顯,說明錨題設計下的累加轉換確實會降低估計精度。當基準年級為低年級時,為了提高垂直量尺化的估計精度,就需要有較大的錨題難度范圍,這是因為錨題難度范圍較大,低一年級學生的題目與上一年級學生的題目重疊可能更多,那么這對于低一年級的學生而言,這是有利的,從而使得垂直量尺化更為順利。實際上,作為低一級年級的學生可能缺乏能力來完成上一年級學生的題目,但若錨題難度范圍不斷變大,則較有可能完成上一年級學生的題目(Lao,2015)。但是,當基準年級為中間年級時,因為其要向兩邊擴充,既要“沖上”(向年級3和年級4轉化),又要“沖下”(向年級1轉化),所以難度范圍的設置不能過于“寬”,也不能過于“窄”,中等的錨題難度范圍則相對更好。

由此可見,在不同的基準年級下進行垂直量尺化,對于錨題難度范圍的選取要求不同。當基準年級為低年級時,建議選取較大的錨題難度范圍;當基準年級為中間年級時,建議選取中等的錨題難度范圍。但是,從高年級選取錨題會比從低年級選取錨題產生更大誤差,這是因為高級學生做低年級學生題目是相對容易的,但低年級學生做高年級學生題目則是相對困難的。基于此,在教育與心理實踐中,為了比較不同年級學生學業能力的發展軌跡,設置有利于低年級學生的錨題難度范圍,對垂直量尺化可能更為受益。

4.5 不同基準年級下年級離散程度與錨題難度范圍的交互效應

以低年級作為基準年級,在年級離散程度為0.5時,年級1、2更適合錨題難度較大范圍,年級3更適合錨題難度中等范圍,年級4更適合錨題難度較小范圍。在年級離散程度為1.0時,年級1、2、3選擇錨題難度中等或較大范圍均可,年級4的表現則非常不穩定,無法選取最佳錨題難度范圍。在年級離散程度為1.5時,只有選取錨題難度較小范圍,才能進行可靠的垂直量尺化。若需要4個年級統一選擇相同的錨題難度范圍,則建議:當基準年級為低年級時,年級離散程度為0.5時,選擇錨題難度較大范圍;當年級離散程度為1.0時,選擇錨題難度中等或較大范圍;年級離散程度為1.5時,選擇錨題難度較小范圍。

以中間年級作為基準年級,在年級離散程度為0.5時,年級1、2、3更適合錨題難度較大范圍,年級4更適合錨題難度較小范圍。在年級離散程度為1.0時,各年級選擇錨題難度較小或中等范圍均可。在年級離散程度為1.5時,各年級更適合錨題難度中等范圍。若需要4個年級統一選擇相同的錨題難度范圍,則建議:當基準年級為中間年級時,年級離散程度為0.5時,選擇錨題難度較大范圍;當年級離散程度為1.0時,選擇錨題難度較小或中等范圍;當年級離散程度為1.5時,選擇錨題難度中等范圍。

綜上所述,基于不同基準年級,年級離散程度與錨題難度范圍存在交互效應(見表1)。

表1 不同基準年級下年級離散程度與錨題難度范圍的交互效應

5 結論

(1)基準年級的選擇會影響垂直量尺化的精度。選擇以中間年級為基準進行垂直量尺化,將會使得垂直量尺化的結果保持在一個較好的精度。

(2)錨題設計下垂直量尺化的轉換不宜超過兩個年級。如果轉換超過兩個年級,那么垂直量尺化精度開始下降。特別地,在年級4上出現了若干Bias和RMSE“極值”,建議與基準年級間隔不宜超過2個年級。

(3)不同基準年級下,年級離散程度越小,估計精度越好。年級離散程度為0.5時,垂直量尺化精度最好,年級離散程度為1.0時次之,年級離散程度為1.5時,精度最差。

(4)不同基準年級下,對錨題難度范圍的選擇應有所不同。當基準年級為低年級時,錨題難度較大范圍時垂直量尺化精度最好。當基準年級為中間年級時,錨題難度中等范圍時垂直量尺化精度最好。

(5)年級離散程度與錨題難度范圍之間存在交互效應。在不同基準年級與不同年級離散程度下,對于錨題難度范圍的選擇應該有所不同。