粒子群優化算法在艦船路徑優化仿真中的應用

方 煜

(天津海運職業學院，天津 300350)

0 引 言

在艦船航行過程中，艦船路徑規劃是否合理直接關系到艦船航行任務能否得以有效完成。因此艦船路徑規劃方法設計是當前的重要研究課題[1]。

多年來，國內外諸多學者對艦船路徑規劃優化方法進行了大量研究，如：張蘭勇等[2]針對傳統RRT*艦船路徑規劃方法進行改進，在艦船路徑規劃過程中，把偏置函數加入其中，使用Dubins 曲線對采樣點實施平滑性連接；楊兵等[3]利用激光雷達圖像對柵格化艦船航行環境信息執行合理生成操作，并通過維諾場算法將危險勢場添加給各柵格，構建艦船航行邊界以及與艦船航行邊界相關的危險度函數，改進A*算法中的評價函數完成艦船路徑規劃與優化工作，對于復雜海洋航行環境中，以上的艦船路徑規劃與優化效果不太理想[4]。

粒子群算法具有路徑尋優速度快、精度高等優勢，為了更為理想的艦船路徑規劃與優化效果，設計了改進粒子群算法的艦船路徑優化方法，并對性能進行測試與分析。

1 艦船路徑優化

1.1 艦船航行海面路線圖構建

將概率圖法其應用于艦船路徑優化工作中，用于對艦船航行路線圖執行有效構建操作。在較為復雜的海面空間中，確定了艦船的出發點以及目的點后，可在剩余區域挑選一個點，利用碰撞檢測的方式對該點執行合理分析操作，若該點隸屬自由空間，便將其當作艦船航行路徑節點，放入路線圖存儲，若該點隸屬威脅空間，則將其清除。把確定的新節點與路線圖中已經存在的路徑節點連接起來，并不斷循環執行此操作，便可完成相應的艦船航行路線圖構建操作，具體過程可歸結為：

1）在艦船航行海洋區域，對艦船航行路徑網絡實施合理構建，并將構建出的路徑網絡標記為U，滿足：

3）用b標記新產生的艦船航行路徑節點，在N中挑選出一些與之相鄰的節點p，并利用局部路徑規劃裝置對局部路徑進行合理規劃。

4）經上述操作后，可將艦船航行所產生路徑的邊界標記為(b,p)，將(b,p)放入E實施合理存儲，與此同時清除掉不具有可行性的艦船航行路徑。

1.2 艦船航行路徑優化模型構建

本文，按艦船在航行性能方面的評價指標，通過執行有效的規劃操作，得到艦船航行路線圖中的最優航行路徑，即獲得一條從艦船出發點Us到艦船航行目的地UG，并滿足一系列約束的艦船航行路徑，該路徑可描述為：

式中： Γ為艦船航行路徑；Ui為路徑節點，i為1～n的整數；n為路徑節點數量。

在復雜艦船航行海面環境狀況下，構建出的艦船航行路徑優化模型為：

式中：Hf為經膨脹化處理操作后獲得的艦船不能夠航行區域集合；f(x,y)=0 為規劃出的用于表示艦船最優航行路徑的曲線，(x,y)為路徑上任意一個點所擁有的坐標； ?(x,y)為船舶實際航行路線；Lg為規劃出最優艦船航行路徑的長度；Lmax為是艦船擁有能源能夠完成航程的最高限值； δg為艦船航行時實際以及規劃出路徑之間存在的偏差； ?i為艦船航行轉彎角； φ為轉彎角最高限值；Sk、 ? 分 別為第k條艦船航行規劃路徑所累計的轉彎角度以及離散性系數；R、ri分別為艦船航行路徑所擁有的轉彎角度最高值、所規劃艦船航行路徑上編號為i的轉向點所擁有的轉彎角度用標記；Smax為艦船航行路徑能夠達到的平滑度最高值；m為艦船航行路徑點的總體數量；e為是一個常指數。

1.3 粒子群優化算法艦船航行路徑優化模型求解

1.3.1 改進粒子群算法

粒子群優化算法利用各粒子間的信息共享以及協作能力搜尋最優解[5]。鑒于其強大的尋優性能，將其應用于艦船路徑優化工作中，使用改進粒子群算法對構建的艦船航行路徑優化模型執行合理求解操作。改進粒子群算法、基本粒子群算法，在艦船航行路徑優化模型求解工作中的不同之處主要有：

1）執行隨機性質權重設置操作。在利用基本粒子群算法對艦船航行路徑優化模型求解時，通常在整個求解過程中，只是采用一個不變的常數值當作慣性權重。如果該常數的值很小，那么在模型求解前期對全局搜索會產生非常不利的影響；如果該常數的值非常大，那么在模型求解后期，又會對局部搜索操作產生非常不利的影響，這無疑會在很大程度上降低模型的收斂速度。為此，通過設置具有隨機特性的權重，避免上述問題發生，設置的隨機性質權重可描述為：

式中：w、wmax與wmin分別為隨機性質慣性權重以及其最大、最小值；rand()為在0～1 中間以相對均勻特征分布的各隨機數；randn()為呈現正態分布特征的隨機值；z為滿足正態分布特征的隨機性質擾動項所擁有的標準性偏差。

2）為擾動性粒子增添有效的更新機制。在利用基本粒子群算法解決艦船最優路徑規劃問題時，各粒子除按經驗搜尋較優越的速度以及位置以外，互相之間只是能夠對種群中擁有的最優粒子所攜帶的信息進行合理共享。如此顯然會降低獲得最優解的概率。不僅如此，若各粒子本身歷史性最優方位與粒子種群所擁有最優方位所產生的方向性夾角過于小，那么還會使算法陷入到局部最優的困境。為此，在基本粒子群算法基礎之上，增添擾動粒子，并為擾動性粒子增添有效的更新機制，用來增強粒子尋優能力。如此操作后，粒子的速度以及位置更新過程可描述為：

1.3.2 改進粒子群算法艦船航行路徑優化模型求解

針對艦船在復雜海洋環境下的最優航行路徑求解問題，本文應用改進粒子群算法對構建的艦船航行路徑優化模型實施合理求解，求解流程如圖1 所示。利用改進粒子群算法求解艦船航行路徑優化模型的最終目的是在構建的艦船航行線路圖中找到一條滿足最優標準的合理解向量。在改進粒子群算法路徑尋優過程中，不同粒子的位置可理解成艦船航行線路圖中的任意航行路徑，在經過各參數初始化、粒子評價以及適應度求解等操作后，經過無數次的迭代操作，便可收獲具有全局性質最優艦船航行性能指標的粒子所表示的艦船航行路徑。

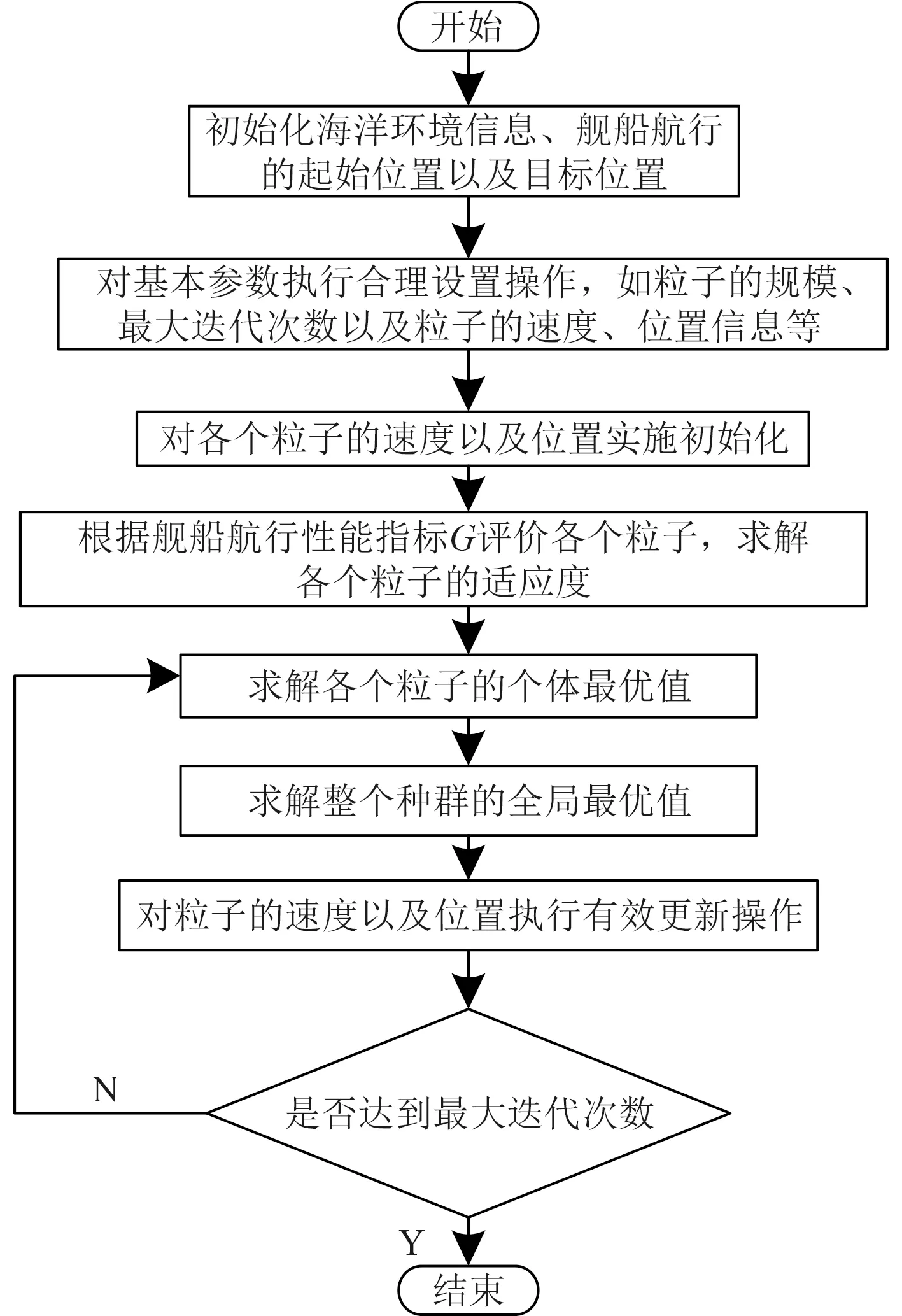
圖1 模型求解流程Fig.1 Model Solving Process

1.3.3 艦船最優路徑平滑優化

通過改進粒子群算法求得的艦船航行最優路徑，盡管在路徑平滑度以及耗能方面，較比其他艦船航行路線具有非常顯著的優勢，但由于其通常還是由若干路徑點構成的折線，因而艦船在完成實際航行任務時，轉彎次數可能仍然會較多，并且當所獲艦船航行最優路徑的某些航段具有非常短的距離時，可能在轉向點位置處，還會出現艦船轉彎角太大的情況，這顯然會對艦船的安全航行造成非常不利的影響。為此，在利用改進粒子群算法獲取到艦船航行初始最優路徑后，將路徑平滑處理操作引入其中，顯著降低艦船航行時的轉彎次數，使獲得的艦船最優航行路徑更具實用性。

對艦船最優航行路徑實施平滑處理的實質是最大限度地進行截彎取直，使用直線對各路徑點實施有效連接，降低艦船在轉彎時的角度，與此同時，讓艦船在各個航段航行時的距離保持合理的長度。對于經改進粒子群算法求得的艦船航行最優路徑序列而言，平滑優化的步驟可簡單歸結為：按所獲艦船最優航行路徑中所顯示的序列順序，以首個路徑點為起點，和最末尾的路徑點連接。如果獲得的線段沒有穿過障礙物，那么可將該段路徑放入路徑序列內，當作艦船全局航行路徑中的子路徑段，反之將其與前方路徑點連接。如此操作，經過無數次循環，一直到倒數第二的路徑點方可停止。這樣便可獲得更為理想的艦船航行最優路徑。

2 實驗分析

以我國某艘國際運輸船為實驗對象，應用Matlab 軟件模擬本文方法對其實施艦船路徑優化過程。據悉該艘國際貨船長度在4 5 0 m 左右，寬在7 0 m左右，單次貨物運載能力可達13200 TEU，其承擔的主要職責是向東南亞某國客戶運輸貨物以及裝備，航行所經海域環境較為復雜。實驗中粒子群優化算法各項參數的設定情況如表1 所示。

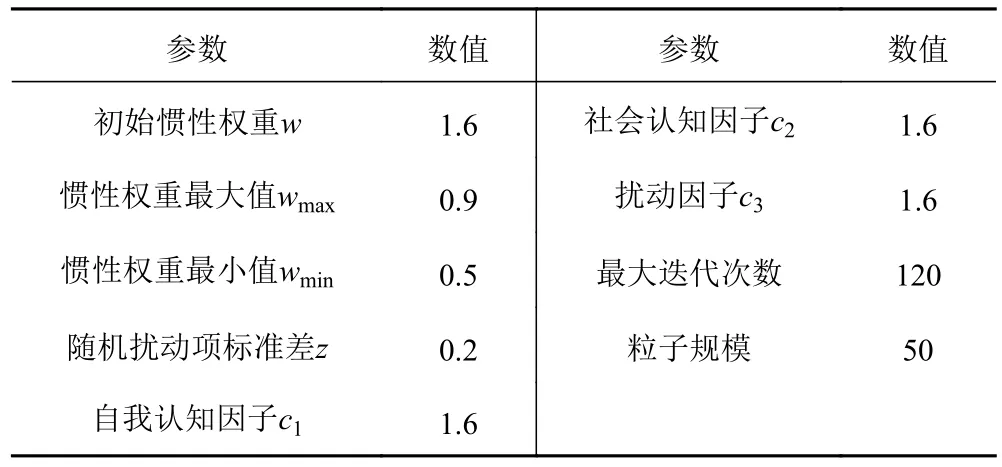
表1 粒子群優化算法參數設定情況Tab.1 Parameter setting of Particle swarm optimization algorithm

應用本文優化仿真方法對艦船航行路徑實施合理優化，獲得的艦船路徑優化結果如圖2 所示。可知，應用本文方法可以實現艦船路徑優化，更好滿足實際工作需要，為艦船續航能力的顯著提高提供可靠保障。

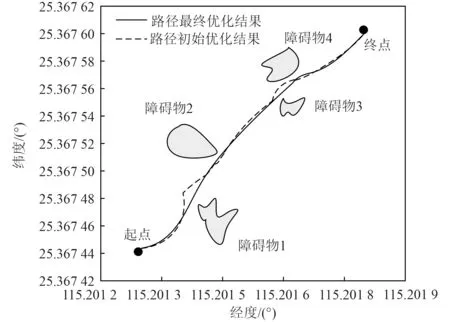
圖2 艦船路徑優化結果Fig.2 Optimization results of ship path

為進一步驗證本文方法在艦船路徑優化方面的有效性，在實驗中設置9 個艦船航行任務，并分別應用基本粒子群算法、改進粒子群算法，對各個艦船航行任務所對應的艦船路徑優化模型實施合理求解，獲得的艦船路徑優化效果對比如表2 所示。可知，應用改進粒子群算法對艦船路徑優化模型實施合理求解后，所獲艦船最優路徑的長度要更短，轉彎點數量要更少，并且最大轉彎角的角度也更小。證明：本文方法在艦船路徑優化工作中優勢顯著，將其應用于實際工作，可收獲更為理想的工作效果。

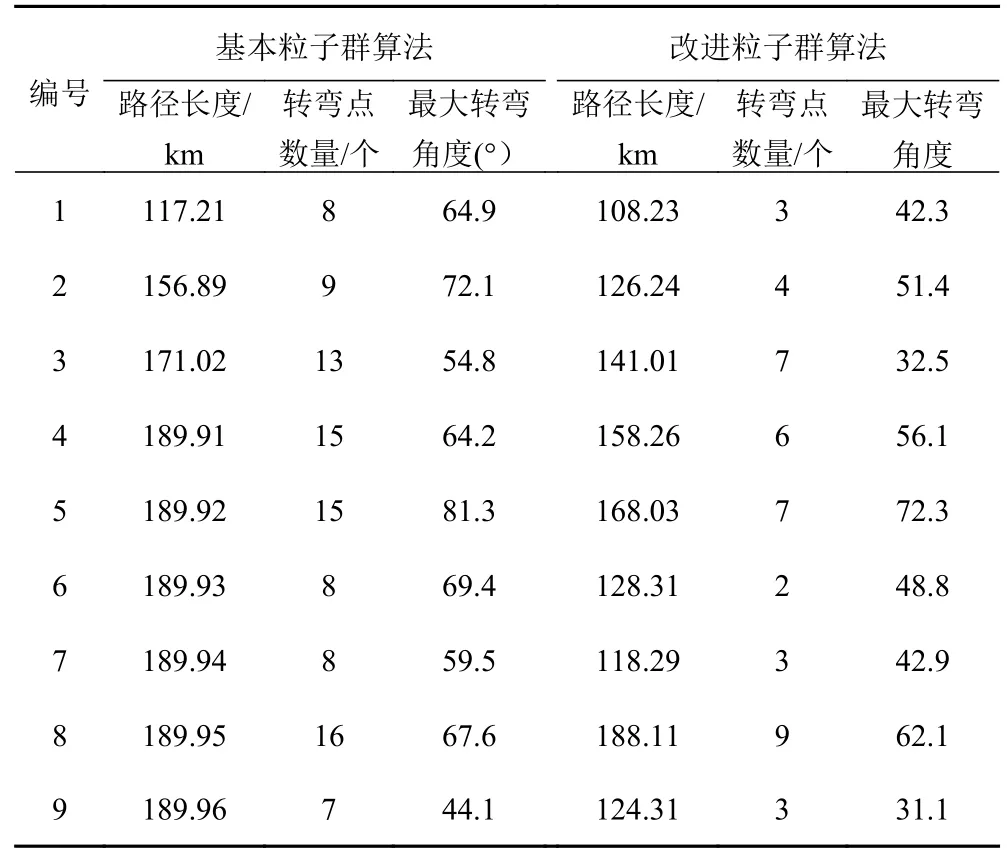
表2 艦船路徑優化效果對比表Tab.2 Comparison of ship path optimization effects

3 結 語

本文方法能夠有效優化艦船路徑，優化后的艦船航行路徑長度更短、轉彎點數量更少、最大轉彎角的角度值也更低，在實際工作中，艦船可更快、更為準確地完成航行任務，若能將其推廣將在軍事以及民事領域產生積極影響。