基于改進SPEA2 算法的多目標航線優化
王 軍,蔣金陽,牛 壯
(大連海事大學 交通運輸工程學院, 遼寧 大連 116026)
0 引 言
隨著海洋運輸在國際商品交換中所占比重越來越大,船舶航線優化被提到了重要的地位。該領域研究的問題是在考慮風浪環境條件的情況下,尋找給定航行的最優路徑和航速,目標通常考慮最小航行時間、燃油消耗或通行風險[1]。
近年來,多目標航線優化得到了較多關注,它可以同時針對多個目標進行優化,進而產生大量的權衡解,決策者可根據當前的需要確定最終的航行方案。目前,進化算法在解決該問題上取得了廣泛應用[2-3],主要包括經典算法SPEA2[4]、NSGA-Ⅱ[5]以及一些改進的算法NMOEA[6]、SPEA2+[7]。然而,由于規劃過程中存在龐大的樣本量和優化空間,收斂效率慢成為普遍現象。特別是隨著迭代步長的增加,搜索樣本量的限制還可能導致算法陷入局部最優。
本文針對SPEA2 在解決多目標航線優化問題中存在的收斂速度慢和易陷入局部最優的現象進行改進。通過Dijkstra 算法搜索的可行解加入到初始種群中作為引導以加快算法尋優的效率;采用更精細化的選擇過程保證精英個體可繼續參與進化;提出新的交叉和變異策略,有效提升了種群質量。
1 SPEA2 算法改進
1.1 SPEA2 的基本思想
Zitzler[4]提出的強度Pareto 進化算法(SPEA2)是一種多目標進化算法,具有良好的搜索性能,它包含一些重要的操作,例如在適應度分配策略中,同時考慮了種群中的顯性個體和隱性個體,提高了全局搜索能力;計算最近相鄰個體的密度提高搜索精度;采用新的存檔截斷方法,保證邊界解得以保留。
1.2 改進工作的動機
大多數優化算法無法找到更高質量的解,主要因為它們工作效率較低。例如,當種群中的大多數解處于非支配階段時,粗糙的選擇方法將剝奪優勢精英繼續參與進化的機會,導致優化結果停滯或更差。同時,交叉機制作為進化算法中生成新個體和擴展解空間的一種有效方法,還尚未被有效探索。尤其當種群中個體間差異較小時,算法易進入停滯狀態,這時應增大變異概率,通過改變種群內個體的部分基因形成新的個體,以跳出局部最優。
1.3 SPEA2 方法的改進
在種群更新階段,改進后的算法只允許非支配個體加入到外部歸檔集A,位于Pareto 前沿端點上的2 個解被強制保留,防止算法陷入局部最優。并且從第T(T≥2) 代開始,將種群P中所有非支配個體與AT-1中的個體進行比較,支配AT-1中任何一方的個體將被遷移到AT中。
在交叉和變異階段,事先給出比較值K,并與選中個體的相似度r進行比較,K的計算公式為:
式中:IDi為組成個體i的基因序列;N為序列的長度;t表示基因值的位置,函數U表示n個個體的基因序列在t位置的非重復值的數量。因此,當種群內個體的基因序列都相同時,K=1;基因序列都不同時,K=1/n。相似度r的計算公式為:
若2 個個體的基因值在t位置相等,則ID1(t)-ID2(t)=0 ,否則為1。 當r≥K,個體間差異較大,利用交叉操作來進行個體間有用信息的交換,來產生更多較好的個體。相反,當r<K時,個體相似度較高,互相值得學習的信息較少,需要對二者進行變異操作以跳出局部最優,增大搜索空間。
2 基于改進SPEA2 的船舶航線優化
2.1 航線優化相關模型的構建
2.1.1 航行環境建模
本文采用大圓航線作為網格系統的參考路徑來擴展航路點,從出發點開始,在大圓航線上每隔距離 ε記錄一次參考點,其中 ε代表天氣預報的空間分辨率。以每個參考點為垂足,生成垂直于當前大圓路線方向的其他路徑點,航路點應只覆蓋在船舶可能行駛的區域內。為避免船舶大幅度轉彎和前往無效的航路點而造成不必要的成本消耗,需在系統中構建連接關系來保證船舶只能在相鄰2 個階段中指定的航路點間移動。本文規定船舶的航行方向分為直行、左轉和右轉,因此系統中從任意一個路徑點出發有可能到達下一階段的3 個不同航路點。
2.1.2 目標函數設計
目標函數是反映航線質量的性能指標,是優化的最終目的。本文以船舶航行時間T和燃油消耗F為優化目標,建立多目標優化函數:
式中:n-1為 航段總數;Si、Vi、 (Te)i分別為船舶在第i階段的航行距離、實際航行速度和主機有效推力。在動力不變的情況下,由于風浪的干擾,船舶實際航行速度較靜止狀態下的速度有所下降,本文采用文獻[8]中的經驗公式,計算在特定的氣象環境和設定的服務航速下船舶的失速損失。
2.2 創建初始種群
初始種群P0在求解的質量和效率上起著很大作用,如果P0包含盡可能多的有利個體,它們可以在迭代過程中不斷引導結果靠近帕累托邊界,同時迭代次數會在大程度上減少。為保證解的多樣性和優良性,采用以下3 種方式來生成P0:一是采用隨機遍歷的方法,在航行區域內隨機生成一條滿足網格系統連接關系的航線,并隨機賦予一個船舶主機功率。二是采用大圓航線作為一部分初始種群,并同樣賦予不同的船舶主機功率。三是采用Dijkstra 算法尋找單目標優化下的最佳航線。
2.3 種群更新
種群中個體質量的好壞通過適應度函數評定。SPEA2 采用細粒度的適應度分配策略,在計算種群P中個體的適應度R(i) 時,種群和外部歸檔集A的個體都考慮在內。而且R值越小,說明支配該個體的個體越少,R(i)=0 表示個體i為非支配解,適應度計算方法為:
當外部歸檔集 |AT|<Q(預設值) 時,通過k臨近算法估算個體密度值,并將特征空間最鄰近的個體逐個剔除,直至 |AT|=Q;相反,若外部歸檔集 |AT|<Q,則根據適應度排序選擇前Q-|AT|個支配解,直至|AT|=Q。
2.4 交叉、變異操作
交叉通過隨機選擇2 個個體共同經過的航路點a(起終點除外),將父代1 從第1 個至第a個航路點的位置信息都復制到子代,第a+1至最后1 個航路點的位置信息從父代2 上復制。在變異個體上隨機選擇一個變異點,使該變異點處的船舶路徑隨機發生改變。操作后的子代和父代共同組成新的種群繼續參與進化。
2.5 檢查終止條件
隨著迭代步數的增加,與最大迭代次數進行比較。如果超過最大迭代次數,則終止算法,否則返回種群更新繼續完成種群進化。
3 仿真實驗與分析
仿真實驗設定的航線起點為橫濱附近(35.25N,141.75E),終點為舊金山附近(37N,122W),分別在3 個月份下進行多目標航線優化實驗,航行環境比較結果如表1 所示。

表1 不同月份下航行環境的比較Tab.1 Comparison of sailing conditions in different months
船舶出發時間設定為每月6 號上午11:00,選擇3500 TEU 的集裝箱船進行仿真,其標準排水量為47202.48 t。為驗證算法的性能,將本文算法與Dijkstra、NMOEA 和SPEA2 進行比較,其中針對3 種進化算法,設定初始種群容量為34,外部種群容量6,交叉概率0.8,變異概率0.2,最大迭代次數100,求解出的Pareto 前沿面如圖1~圖3 所示。
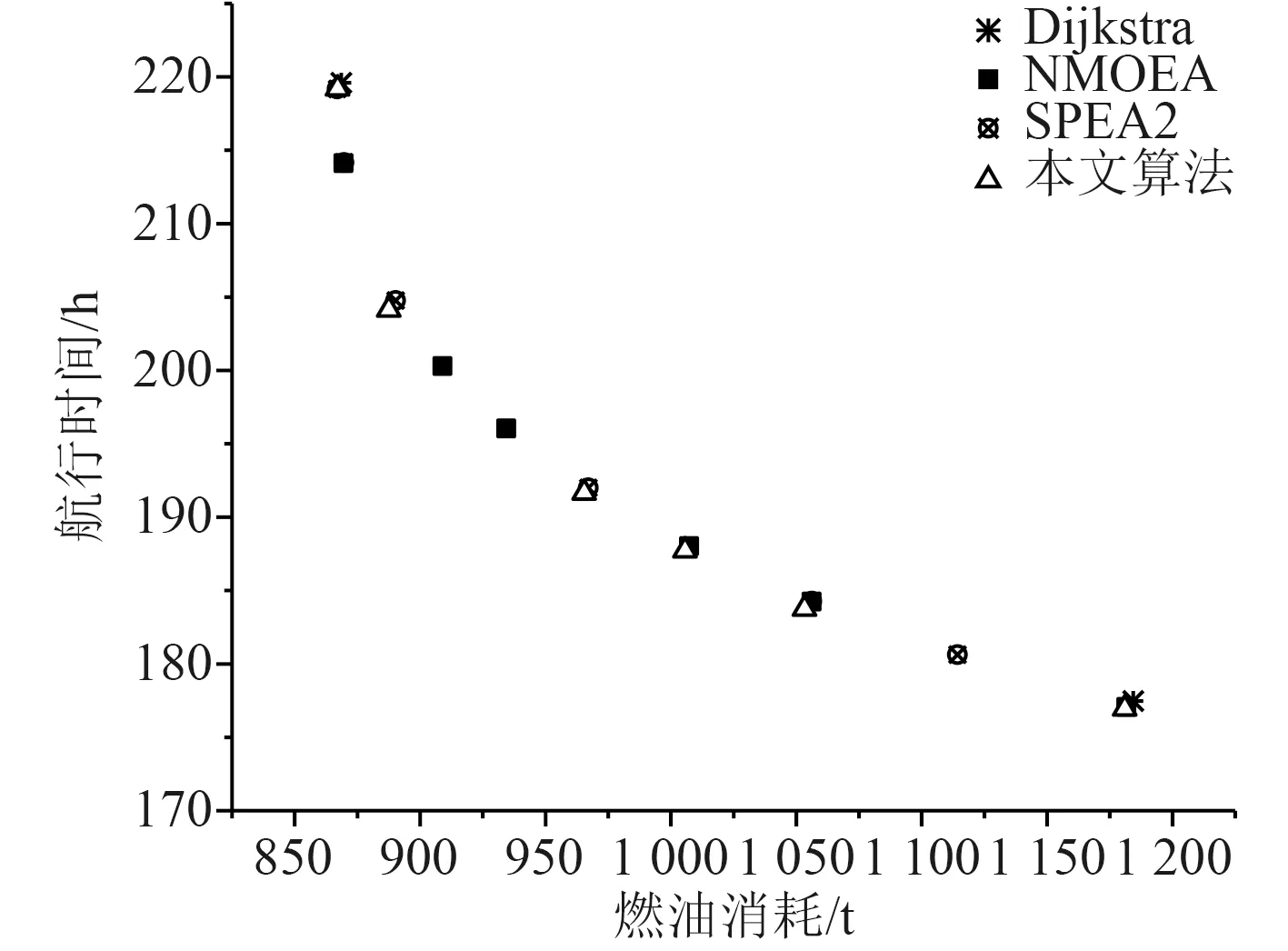
圖1 2018 年7 月的Pareto 前沿面Fig.1 Pareto frontier in July 2018
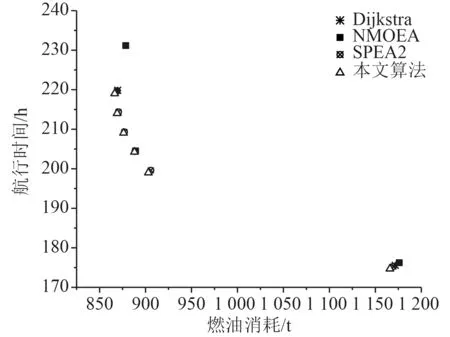
圖2 2018 年4 月的Pareto 前沿面Fig.2 Pareto frontier in April 2018
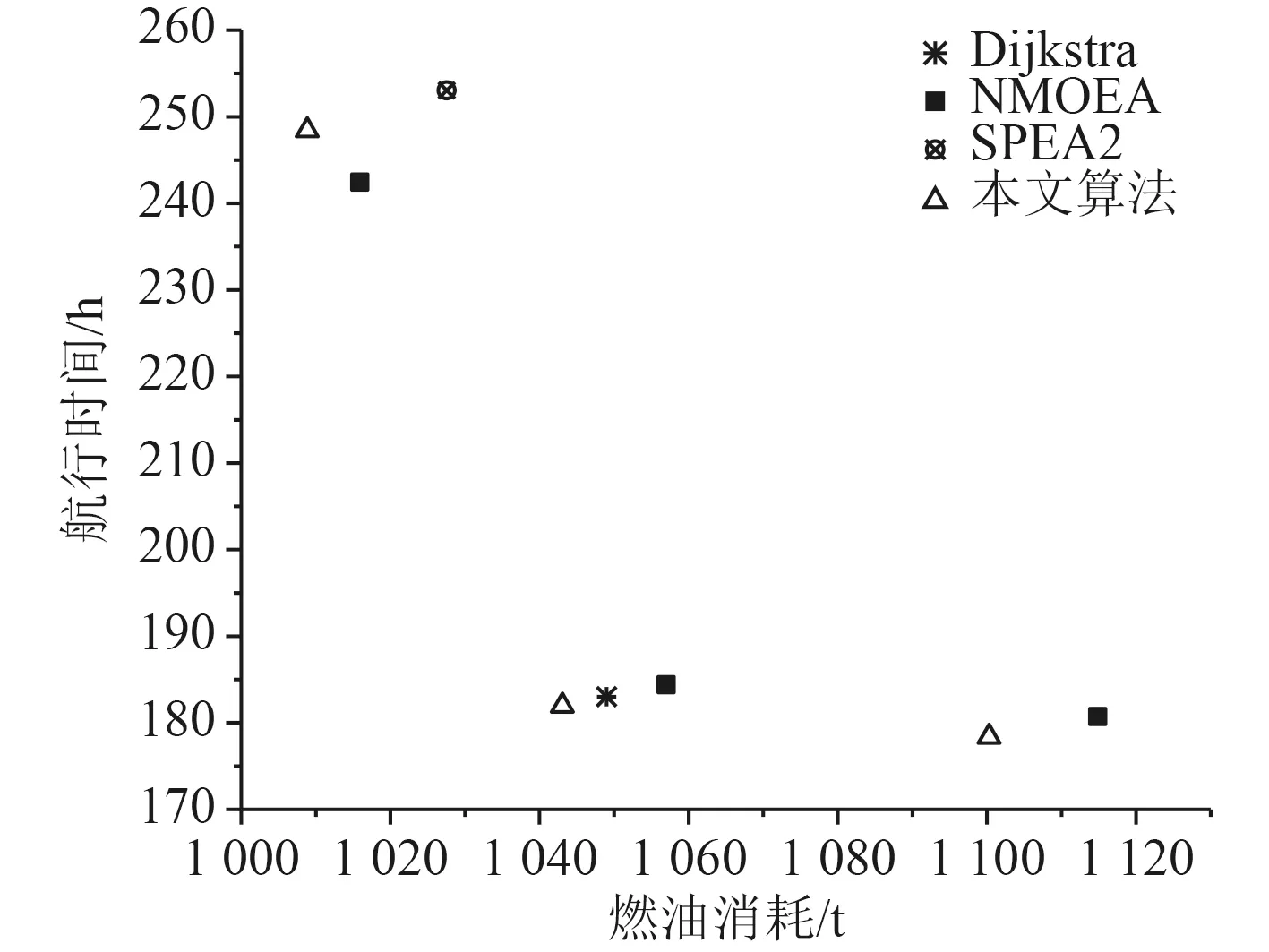
圖3 2018 年1 月的Pareto 前沿面Fig.3 Pareto frontier in January 2018
實驗結果顯示,進化算法求得的解在時間和油耗上均優于Dijkstra 算法得到的結果。另一方面,本文提出的算法在收斂性上優于NMOEA 和SPEA2,且隨著氣象的變差,優勢表現越明顯。從多目標進化算法性能評價指標-超體積(HV)[9]的角度對結果進行數學分析。表2 比較了3 種進化算法求得解的HV值,HV 值越高,群體中個體的綜合表現越好。將(1120,260)做為參考點進行HV 的計算,結果顯示本文提出的算法綜合性能最高,其次SPEA2,最差的是NMOEA。圖4~圖6 分別展示了3 個月份下的Pareto 航線集,對于海況較好的7 月和4 月,該月份下的航線集主要是以Dijkstra 求得的航線為基礎并對其優化。優化部分主要集中在航線的后半段,但在海況較差的1 月份,它的Pareto 航線集不僅包含Dijkstra 的結果,還包括隨機路線,這些路線光滑度較低,但在省油和省時方面仍優于Dijkstra 結果。
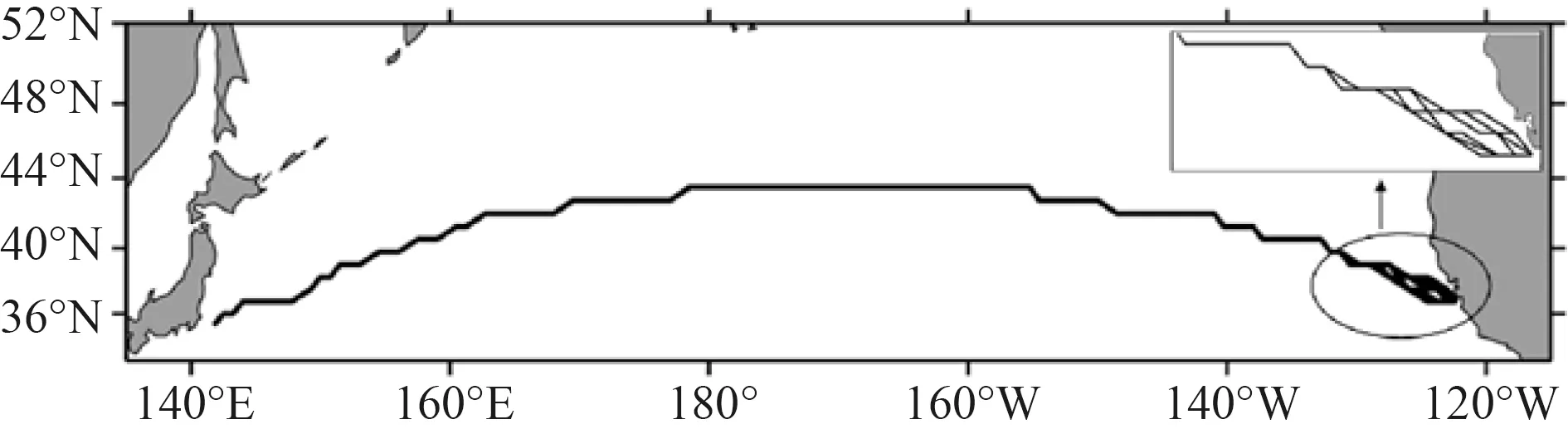
圖4 2018 年7 月的Pareto 航線集Fig.4 Pareto route set in July 2018
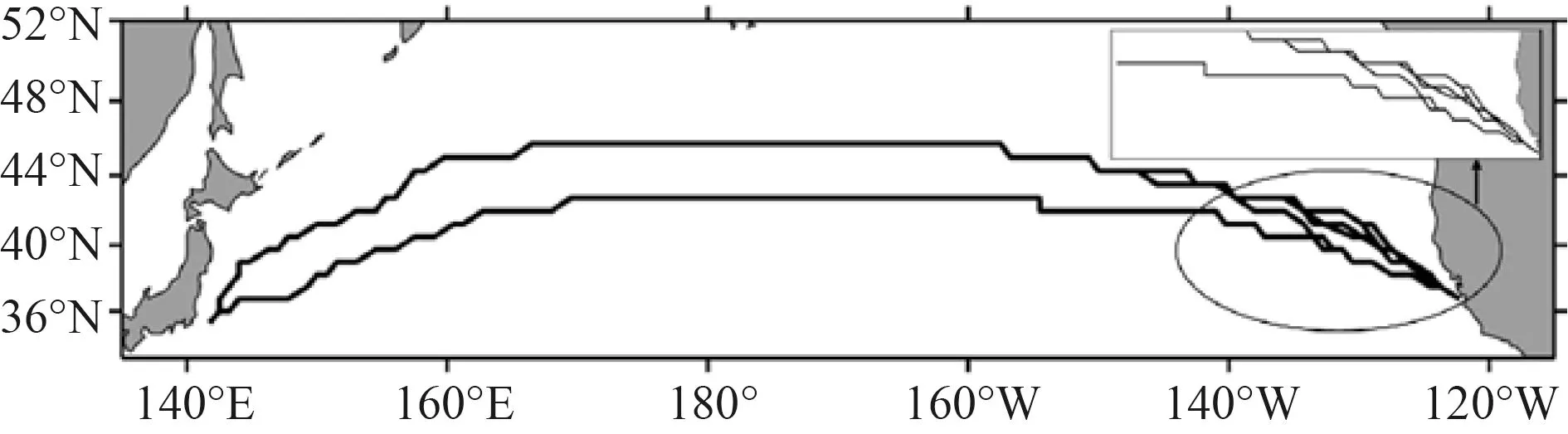
圖5 2018 年4 月的Pareto 航線集Fig.5 Pareto route set in April 2018
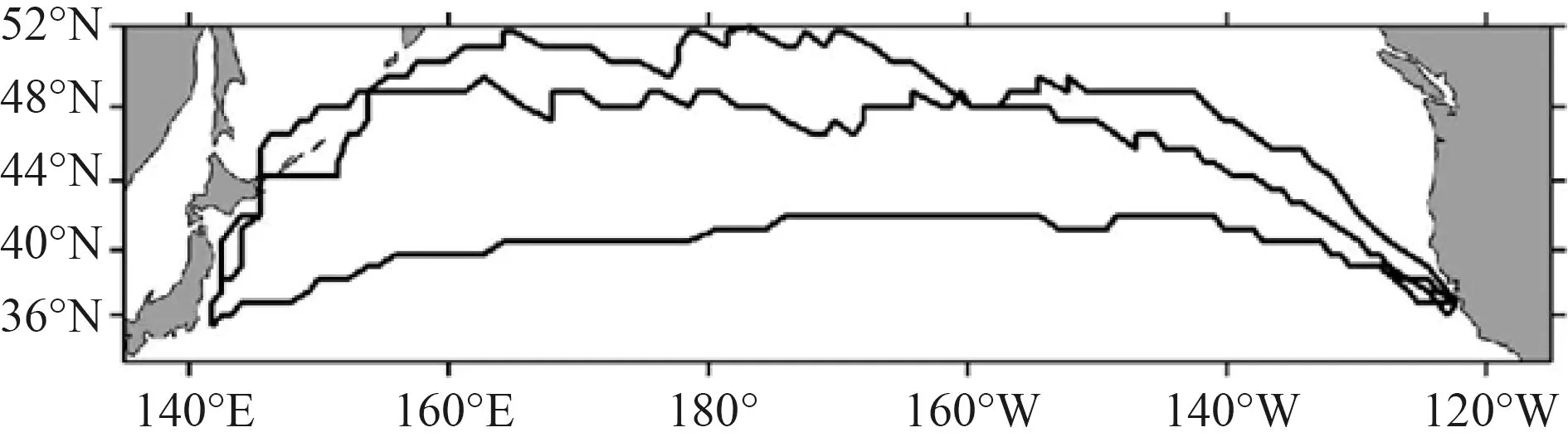
圖6 2018 年1 月的Pareto 航線集Fig.6 Pareto route set in January 2018
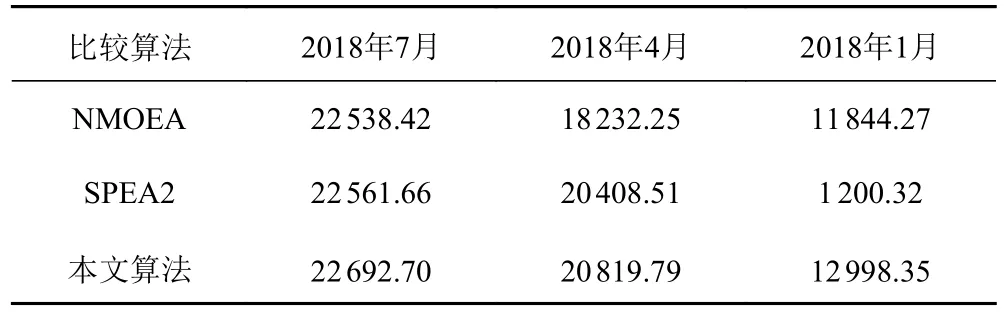
表2 進化算法的HV 結果比較Tab.2 Comparison of HV results of evolutionary algorithms
4 結 語
針對多目標航線優化問題,本文構建了燃油成本和航行時間最小的雙目標優化模型,并設計了基于SPEA2 的引導性多目標進化算法。通過在初始種群中加入Dijkstra 算法得到的單目標優化結果,以此作為引導,并在種群更新階段進行改進,保證了具有代表性的精英個體繼續參與進化。為避免種群優良基因的破壞以及陷入局部最優,對交叉和變異機制進行改進。最后以太平洋航線為例,在不同海況條件下進行仿真實驗,驗證了算法的高效性。與NMOEA 和SPEA2 多目標進化算法的求解結果進行對比,證明本文算法具有較好的收斂性和全局尋優能力。

