抽水蓄能電站尾水管水柱分離數值模擬

肖鵬飛，趙志高，楊桀彬，劉程鵬，何相慧，楊建東

［1．中國長江三峽集團有限公司科學技術研究院，北京市 101100；2．水資源工程與調度全國重點實驗室（武漢大學），湖北省武漢市 430072］

0 引言

隨著風光新能源的發展，抽水蓄能成為新型電力系統中的基礎性調節電源。根據《抽水蓄能中長期發展綱要》，中國抽水蓄能裝機將翻兩番，達到1.2 億kW。在資源儲備站點日益緊張的背景下，抽水蓄能向著高水頭、大容量、長輸水管道方向發展。抽水蓄能機組復雜的流道布置、頻繁的工況切換[1]可能導致水力系統出現較大的水錘振動、液柱分離甚至空化空蝕現象[2]。如何準確模擬尾水管液柱分離對判別抽水蓄能運行安全性、確定機組安裝高程具有重要意義。

國內外研究學者在20 世紀80 年代就對伴有空穴流、液柱分離的氣液兩相瞬態過程展開了研究。楊建東[3]從空化和氣液兩相流理論兩個方面，采用理論與實驗相結合的方法，系統地研究了空化流動與液核分離的瞬態過程，為今后進一步研究其瞬態過程的機理、數值分析和滿足實際需要奠定了基礎。蔣勁等[4]給出了一種考慮兩相間物質質量交換、管壁流質相互作用的一維計算模型。周領等[5]將Wylie[6]提出的離散空腔模型（DGCM）和有限體積法Godunov 格式結合起來計算水柱分離。楊桀彬[7]在集中空穴模型和氣泡均勻分布模型的基礎上提出了以臨界空穴率作為水柱分離的充分條件的氣液兩相流計算模型。何相慧[8]在抽水蓄能機組動態特性實驗平臺上開展了水柱分離模型實驗，給出了尾水管發生水柱分離的判別條件。

本文基于有限體積法（FVM），引入空穴率α描述氣體體積，采用二階Godunov 格式離散雙曲型偏微分方程，對含氣型氣液兩相流以及相變下的瞬態過程進行了數值模擬，尤其是摒棄了Wylie 離散空腔模型，直接采用空化模型封閉方程組，并通過工程實例與傳統計算方法進行對比。

1 氣液兩相流及空化模型

1.1 基于有限體積法的氣液兩相流模型

為了衡量管道中含氣量變化，引入量度氣液兩相流中氣泡含量大小的參數，容積空穴率α，其表達式為：

式中：W——體積；

g和l——氣相和液相；

L——管道長度；

A——段面橫截面面積。

氣液兩相瞬變流的基本方程仍然是動量方程和能量方程，應對氣相和液相分別列出。對于含氣型氣液兩相瞬變流中氣相體積較小（α<0.15）的情況，氣泡會跟隨液體一起運動，于是忽略動量交換，將動量方程合并為一個。而連續方程仍保留分相的形式，以便計算氣液兩相之間的質量交換[9]。

類似單相流體動量方程推導方法，可得到含氣型氣液兩相瞬變流動量方程：

式中：p——管道中心點壓強，Pa；

V——流速，m/s；

x——從任意點開始的沿管道軸線的坐標距離，m；

t——時間，s；

α——空穴率；

ρg——氣相密度，kg/m3；

ρl——液相密度，kg/m3；

D——管道直徑，m；

f——達西-威斯巴哈（Darcy-Weisbach）系數；

g——重力加速度，m/s2。

連續性方程的本質是質量守恒方程，為考慮兩相之間的質量交換，將兩相間的質量變換率=dm/dt引入單相流的連續方程，可以分別寫出氣相和液相的連續方程：

對上述方程進行變形再通過有限體積法進行離散，得到計算表達式：

式中：Fi+12(UL,i+12,UR,i+12)，Fi-12(UL,i-12,UR,i-12)——界面i+1/2，i-1/2的數值通量；

UL和UR——界面左右的變量值。

1.2 變波速模型與相變模型

在參考文獻[9]中，給出了波速方程：

式中：a——水錘波波速，m/s；

C1——管道固定方式系數；

E——管道彈性模擬量；Kg和Kl——氣體容變彈性模擬量和液體容變彈性模量。

對于空化現象的數值模擬，需要定量描述氣液之間的物理相變過程，關鍵在于建立或選取合適的空化模型。空化模型是用于描述氣相和液相之間質量交換的數學模型，目前應用較為廣泛的空化模型主要分為兩類：

（1）基于正壓流體狀態方程的空化模型；

（2）基于質量輸運的空化方程[10]。

本文采用的計算模型需要定量考慮氣液兩相之間的相變關系，故選取基于質量輸運的空化模型。有壓管道的空化現象，往往伴隨著氣泡的破碎和融合，在極短的時間內就會發展為空化空腔，因而基于單個氣泡的空化模型也不適用于方程的計算和求解。最后基于相變物理本質，選取了以Singhal 模型為基礎的空化模型進行數值模擬分析，并根據氣液兩相管流實際情況對公式參數進行了優化。

式中：Vch——特征速度，它反映了液體和蒸汽之間局部相對速度的影響，通常認為大空隙不移動，所以Vch=V；

σ——表面張力系數。

在該模型中，特征速度、表面張力系數、不可凝結氣體的影響也被考慮在內，因而被稱為 “全空化模型”。

2 有限體積法和特征線法的耦合

2.1 計算模型

在抽水蓄能管道系統中，可能發生空化的區域較少，實際上一般只發生在尾水管進口。其中尾水管發生的空化和液柱分離會對水輪機和水力系統造成極大影響。在實際工程中，往往降低安裝高程以防止尾水管內的壓力降至蒸汽壓力以下[11]。而需要重點關注的也是尾水管部分的空化現象。

因此，同時考慮尾水管部分空化模擬的準確性和計算效率，提出了兩個解決方案。

（1）將FVM 和MOC 方法進行耦合，采用FVM 計算尾水管，MOC 方法計算抽水蓄能電站其余水力單元。

（2）尾水管的FVM 模擬計算和其他部分的MOC 模擬計算采用不同的時間步長進行耦合。

基于Riemann 不變量，有限體積法在邊界上有以下方程：

結合特征線法基本邊界方程：

如圖1 所示，對于MOC 下游邊界和FVM 上游邊界，也就是邊界1 耦合，通過式（9）、式（10）以及邊界方程聯立可求解。類似地，對于FVM 下游邊界和MOC 上游邊界，也就是邊界2 耦合，通過式（8）、式（11）以及邊界方程聯立可求解。

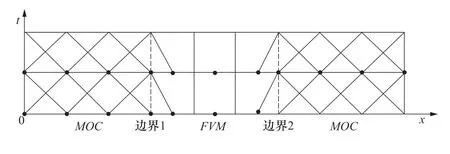
圖1 邊界耦合示意圖Figure 1 Schematic diagram of boundary coupling

2.2 方法驗證

如圖2 所示，采用串聯點作為邊界耦合點，對于上庫-閥門簡單的管道系統，壓力管道L1 和壓力管道L2 的長度均為1000m，糙率n=0.014。

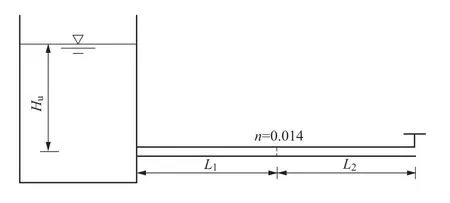
圖2 水庫-閥門系統Figure 2 Reservoir-valve system

上游庫水位20m，閥門流量由4m3/s 在0 時刻減為0m3/s。

對于管道L1 采用FVM 進行數值模擬計算，對于管道L2采用MOC 進行數值模擬計算。方案一FVM 和MOC 時間步長均為0.04s；方案二FVM 時間步長為0.04s，MOC 時間步長為0.2s。

閥門處測壓管水頭隨時間變化值如圖3 所示。顯然，在不同時間步長下耦合計算結果較為吻合，說明該耦合方法可用于管道瞬態過程模擬。

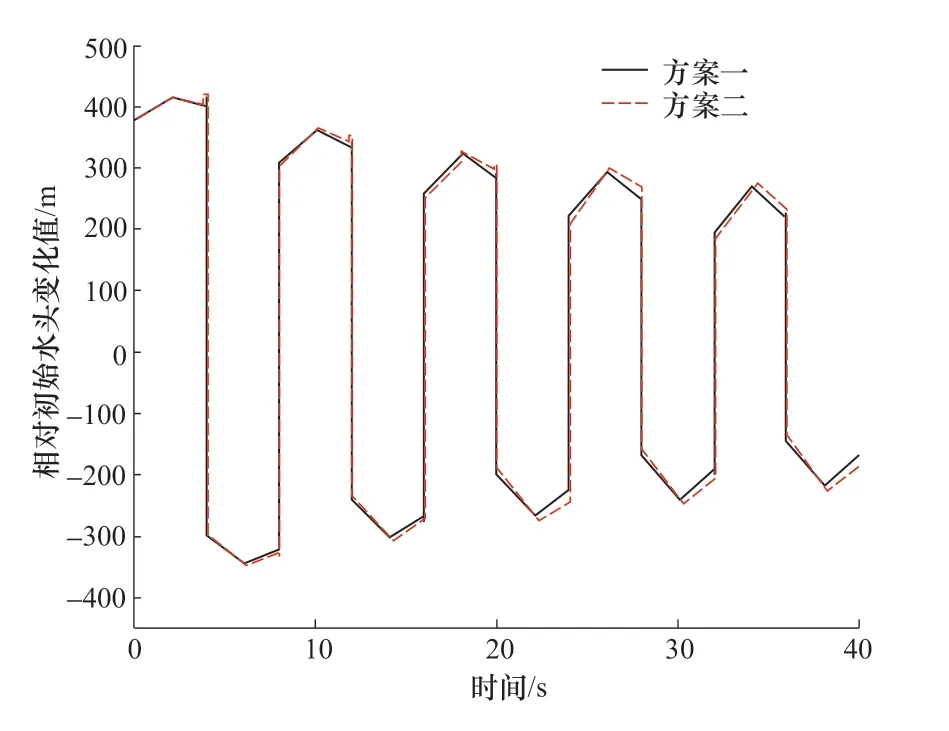
圖3 閥門測壓管水頭Figure 3 Valve gauge head

3 工程應用

3.1 工程計算模型

以某抽水蓄能電站為例，該電站為一洞四機方案，設有下游調壓室，管道示意圖如圖4 所示。機組號為1 號、2 號、3 號和4 號，機組及管道其他參數如表1 所示。

表1 某抽水蓄能電站運行參數Table 1 Operating parameters of a pumped storage power plant

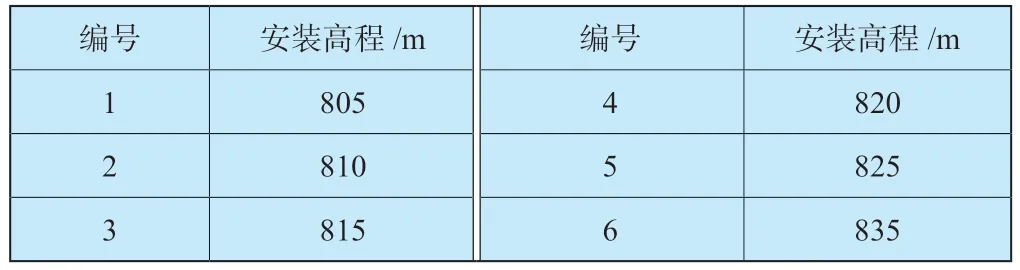
表2 某抽水蓄能電站運行參數Table 2 Operating parameters of a pumped storage power plant

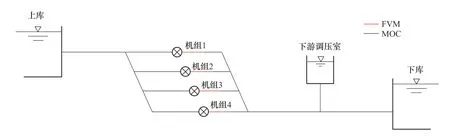
圖4 某抽水蓄能電站管線布置示意圖Figure 4 Schematic diagram of pipeline layout of a pumped storage power plant

本文研究抽水蓄能電站尾水管空化和液柱分離受安裝高程的影響情況。尾水管部分采用FVM 方法建模計算，其他部分采用MOC 方法計算。同時，為了兼顧計算效率和準確性，FVM 部分取0.001s 時間步長計算，MOC 部分取0.01s 時間步長計算。

計算工況為該工程過渡過程大波動尾水管進口壓強的最不利工況CT4-5：上庫正常蓄水位1262.5m，下庫死水位873m，四臺發電機組均以額定出力運行。在0時刻，同一水力單元3號、4 號機組甩符荷，1 號、2 號機組5s 后甩負荷，導葉緊急關閉。

3.3 安裝高程敏感性分析

為研究空化和液柱分離對于抽水蓄能電站尾水管進口壓強的影響，本次數值模擬，選取了6 組不同機組安裝高程進行計算，并對1 號機組尾水管進口壓強進行分析。計算結果以相對壓強對應的壓強水頭為準。

6 組數值仿真模擬試驗計算結果如圖5 所示。顯然，在不考慮壓力脈動和計算誤差的情況下，安裝高程從初始的805m 上升到825m 時，尾水管進口壓強隨著安裝高程上升而不斷下降，波形完全一致。當機組安裝高程上升到830m 時，尾水管進口壓強會下降到汽化壓強以下，進而發生空化。

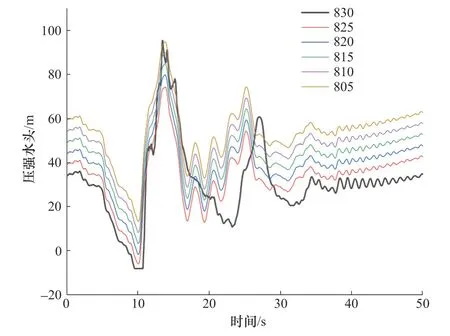
圖5 不同安裝高程尾水管進口壓強水頭Figure 5 Tailpipe inlet pressure head at different installation elevations

3.3 水柱分離模擬對比

圖6 給出了初始安裝高程為830m 條件下，運用FVM 采用空化模型和不采用空化模型兩種方法對1 號機組尾水管進行數值模擬的計算結果。采用空化模型計算，尾水管進口壓強達到汽化壓強時，壓強不再下降，出現空化和液柱分離，之后的最大升壓相比初始壓強上升62.85m。而不發生空化的數學模型計算結果最大升壓相比初始壓強上升38.15m，遠小于發生液柱分離后的壓強升高值。并且發生液柱分離后壓強上升速率更快。同時，發生液柱分離后會使得波速降低，進而水錘波動周期向后推移。在導葉完全關閉后，尾水管進口壓強趨于穩定，與無空化模型計算結果相似。

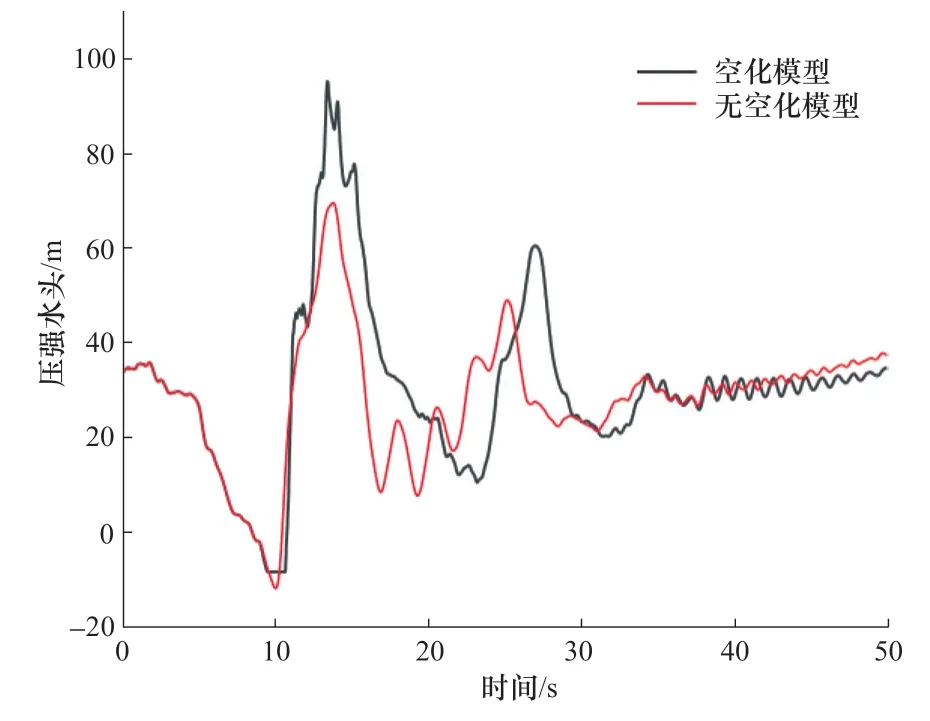
圖6 尾水管進口壓強水頭Figure 6 Tail pipe inlet pressure head

圖7 單獨給出了通過FVM 空化模型計算得到的尾水管進口壓強隨時間變化曲線圖。在0 時刻，3 號、4 號機組導葉瞬時關閉，受此影響，機組尾水管壓強緩慢下降。5s 時刻，該機組導葉開始關閉，尾水管壓強開始迅速下降，并在9.35s 時刻達到汽化壓強，壓強停止下降，尾水管進口發生空化，進而出現液柱分離。10.93s 時刻，如圖7 中1 點所示，下游增壓波到達尾水管進口，液柱彌合，同時液柱分離處出現兩個反射波，增壓波到達液柱分離處，受空穴反射為減壓波向下游傳播，而在這同時，增壓波繼續向機組傳播，在機組處反射為增壓波向下游傳播。受到增壓波影響，尾水管壓強迅速上升，如圖7 中2 點所示。在13.48s 時刻，二次反射增壓波到達尾水管進口處，形成液柱分離水錘的二次升壓，升壓極值為95.21m，遠大于不發生空化的升壓極值70.52m。

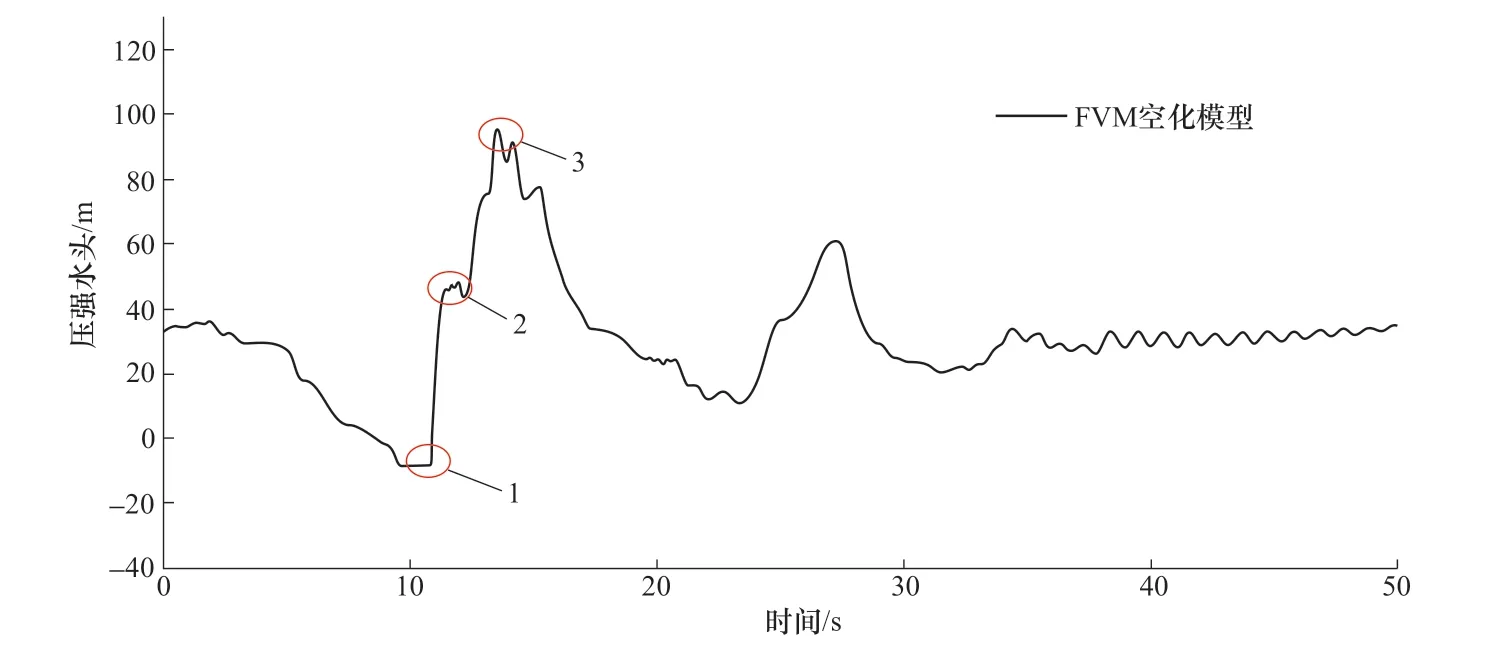
圖7 尾水管進口壓強水頭Figure 7 Tail pipe inlet pressure head

4 結論

本文基于特征線法和有限體積法，引入相變空化模型并耦合邊界條件方程，提出了一種抽水蓄能機組水柱分離計算新方法，在不考慮壓力脈動和計算誤差情況下，實現了對該電站尾水管空化過程的一維數值模擬，并闡明了水柱分離過程中尾水管進口壓強的動態演變規律。該方法克服了傳統特征線法不能模擬抽水蓄能水柱分離現象的局限性，為抽水蓄能電站安裝高程設計及安全穩定運行分析提供了有效工具。