發動機試驗動態數據處理方法綜述

劉子星 ,高 俊 ,宋炯亮 ,林 萌 ,楊 懿

(1.北京動力機械研究所,北京10074;2.北京航天試驗技術研究所,北京 100074)

1 引言

發動機試驗是解決發動機研制過程所遇到的問題、推動理論研究和完善發展發動機設計理論的基本途徑,也是分析發動機技術參數和評估發動機性能和評判發動機能否定型的重要方法[1]。在發動機試驗中,各種測量數據是研究發動機性能、定位各類型故障、計算可靠性等的重要依據。

數據處理是將反映物體狀態的物理量隨時間變化的原始信號轉換成某些適合于工程設計、試驗和分析的簡化量。數據處理貫穿于發動機設計、試驗和生產的各個階段,其目的是揭示動力學環境、制定試驗條件、設計準則以及診斷故障和提供信息[2]。

對發動機試車的動態參數進行分析是研究發動機各項性能指標的重要依據。例如,分析推進劑的流量數據能夠精確計算發動機比沖和混合比。分析推力和穩態壓力能夠研究發動機實際工作性能以及發動機與試車臺之間的協調性。推力室脈動壓力是研究發動機啟動特性與不穩定燃燒、管路特性和定位發動機故障原因的重要依據。振動參數是研究推力室、燃氣發生器、渦輪泵等關鍵部件結構性能、不穩定燃燒狀態等非常重要的參考依據。因此,研究動態數據的分析和處理方法,不僅關系到發動機零部件的性能評價,也是準確評估發動機總體性能、發動機和試車臺匹配程度等的重要依據。

目前,隨著數字信號分析技術的發展,業內研究人員對動態數據分析已經由最初單一的傅里葉變換分析發展到小波分析、小波包分析、Hilbert-Huang 變換、人工神經網以及多種分析方法相結合的靈活運用和推廣[3,4]。在本文中,總結了上述多種方法的理論特征,梳理了該方法在動態數據分析領域的應用情況,為深度挖掘試驗數據信息、提高發動機性能和提高發動機設計能力提供了參考依據。

2 發動機試驗動態數據處理方法

2.1 FFT 方法

快速傅里葉變換(FFT,1965)的基本思路是將時域采樣點數分解為組合因子,按照組合因子將整個數據序列分割為若干子序列。先計算各子序列的離散傅里葉變換,然后將子序列變換結果加以合成,從而得到整個序列的離散傅里葉變換[2]。該方法的局限性在于缺乏分析時域內局部頻率數據的能力。

在工程應用中,采用計算機對時域連續傅里葉變換進行離散化時會不可避免地產生一些問題:

(1)時域離散化引起頻域的周期延拓,很可能產生頻率混淆;

(2)時域的截斷引起泄漏;

(3)頻域的離散化引起時域的周期延拓。

為解決上述問題,諸多研究人員制定了相應的解決辦法,如加入抗混濾波器、窗函數、提高采樣率等[2]。

目前,FFT 方法已經廣泛應用于航空、航天發動機試驗振動數據和脈動壓力數據等的分析處理中[5-8]。

胡海峰等根據R 語言在統計分析方面的優勢,在VC 軟件平臺結合R 語言的編程實現發動機數據分析處理。采用FFT 方法分析點火啟動及拖尾段的含噪波動數據,根據時域內振動信號的頻譜圖,識別信號高低頻的有用信息[9]。

孫百紅等系統歸納了FFT 方法對液體火箭發動機試驗振動數據進行分析的步驟和路線。采用FFT 分析方法對某型號液體火箭發動機試驗出現故障的穩定段振動數據進行頻譜分析,通過對比正常數據的幅頻特性,成功定位某試驗件結構破損的故障。通過對振動數據RMS(Root-Mean-Square,均方根)特性分析,繪制振動數據特征頻段全程瀑布圖,能夠有效識別試車中的故障[10]。

牛偉等將航空發動機轉速高齒信號作為分析發動機振動狀態的基礎,提出了基于FPGA 的振動信號采樣設計流程:采樣-濾波抽樣-三次樣條插值-信號抽取-傅里葉變換,制定了振動數據頻域特征提取處理流程。通過對試驗數據進行分析,證明該方法不僅運算簡單、分析精度高、實時性強,而且有效解決了FFT 方法分析過程中的頻譜泄露和柵欄效應等問題[11]。

楊懿等針對液體火箭發動機脈動壓力數據采樣率高和系統響應頻率快的特點,采用FFT 方法對脈動壓力數據進行分析。根據脈動壓力數據的頻譜特性,結合推力室軸、徑向和切向三個振動測點的數據,有效定位發動機不穩定燃燒的聲振類型[12]。

陳子豪等為了驗證固體火箭發動機試車過程中因不穩定燃燒所產生的壓強異常升高和發動機推力值異常振蕩的問題,采用FFT 方法分析推力室壓強的幅頻特性和燃燒器的試驗數據,得到壓強振蕩的倍頻關系,結合聲學仿真的結果,證明該方法能夠有效分析發動機不穩定燃燒的機理[13]。

洪亮等采用FFT 方法,通過統計分析轉子在不同轉速下的倍頻特征和振動量級之間的關系以及轉子臨界試驗中的幅頻特性,得出了轉子發生故障的特征和原因,為優化和提高發動機設計提供了重要的參考依據[14]。

鐘永恒等針對航空發動機外部管路流固耦合振動是導致發動機外部管路故障的重要因素之一,根據所推導的直管管路流固耦合偏微分方程建立管路系統物理模型,采用C++語言開發了仿真分析軟件,研究MOC-FFT 方法分析計算外部管路時頻響應特性和固有頻率。通過動態壓力特性試驗,驗證了該模型的有效性和準確性[15]。

發動機試車過程中,不同系統之間往往存在關聯,因此,通常將不同測點的脈動壓力數據、振動數據等結合起來進行分析,便于分析發動機的性能和故障定位。

以某型號發動機試驗為例,將振動測點數據和推力室脈動壓力數據[12]的分析相結合。脈動數據采樣率為10 kHz,穩定段0.02 s 的數據如圖1 所示。

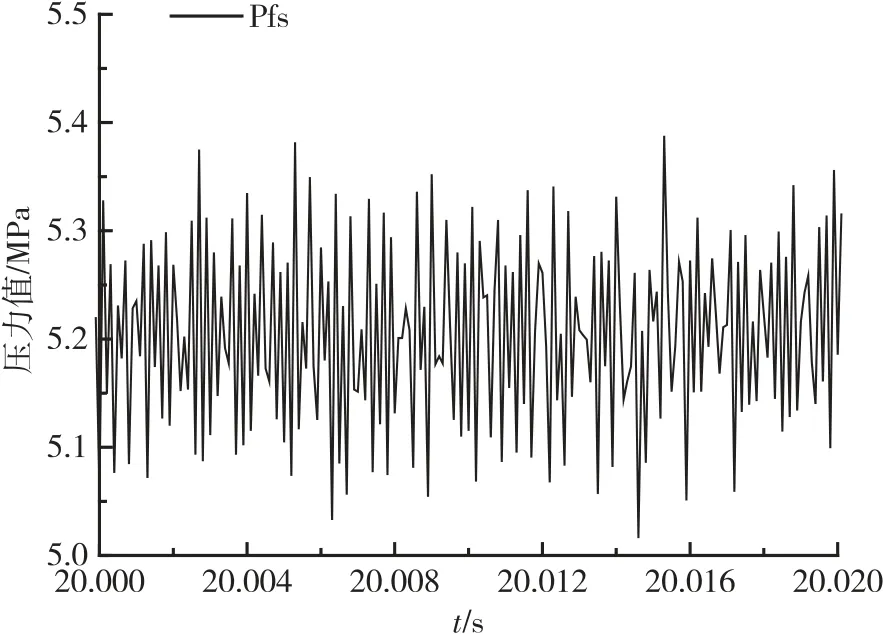
圖1 推力室脈動壓力數據圖Fig.1 Fluctuating pressure data diagram of thrust chamber

采用FFT 方法對脈動壓力數據進行頻譜分析,0～11 000 Hz 頻率段的頻率-幅值特性曲線如圖2所示。

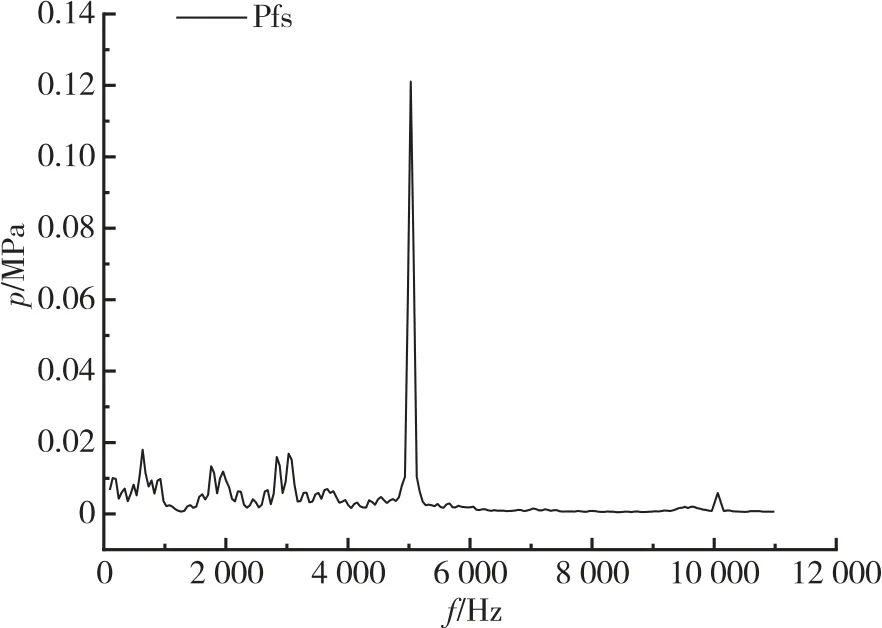
圖2 推力室脈動壓力數據FFT 頻譜圖Fig.2 FFT spectrum of fluctuating pressure data

分析圖2 的幅頻曲線,推力室脈動壓力的幅值峰值主要集中在0～5 500 Hz 的頻率段內,5 500～10 000 Hz的高頻段幅值曲線較為平坦。在中、低頻段,500～3 500 Hz 幅值存在多個小幅度波動,可能與發動機工作倍頻有關系。5 000 Hz 左右存在一個高峰值波峰,可能與發動機中頻共振和不穩定燃燒有關。對于脈動壓力數據頻譜分析需要結合發動機振動數據進一步分析。采用FFT 方法對推力室軸向、徑向和切向三個振動測點數據進行分析,其中徑向測點ab1-2 的頻譜分析結果如圖3 所示。

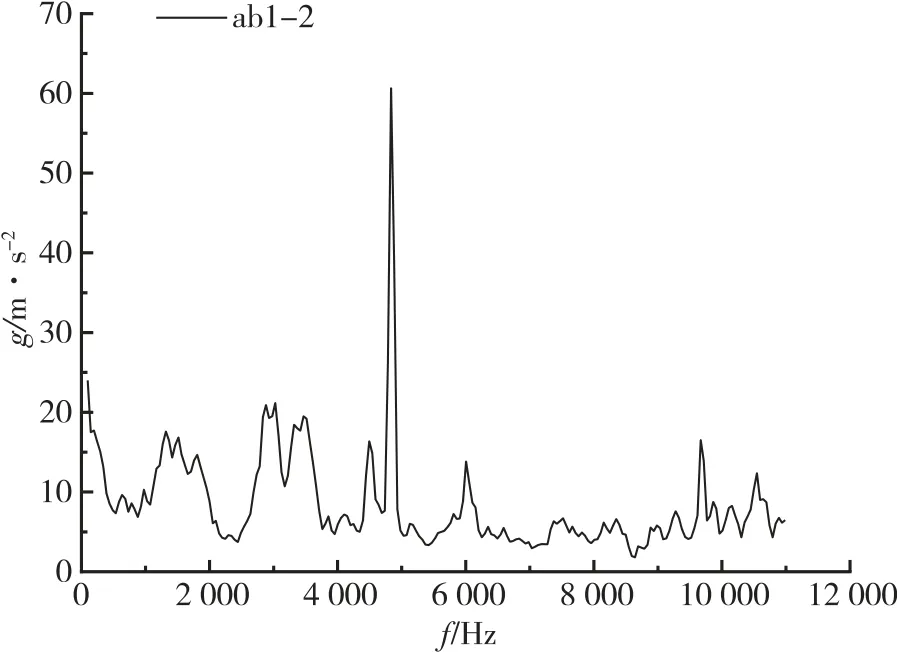
圖3 推力室徑向振動測點FFT 頻譜圖Fig.3 FFT spectrum of radial vibration measuring point

從圖3 可知,徑向振動測點在1 000～5 000 Hz低頻率段中存在多個幅值峰值,5 000 Hz 左右也存在一個高峰值波峰,說明脈動壓力數據與徑向振動測點存在關聯。對脈動壓力、推力室軸向、徑向和切向振動測點數據FFT 頻譜分析結果如表1 所示。

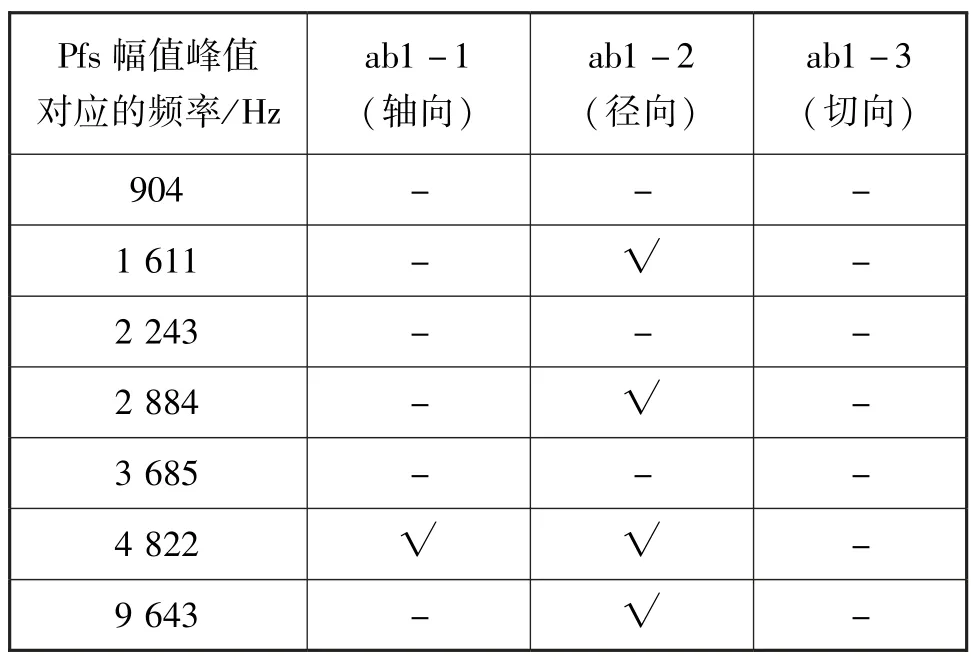
表1 推力室振動測點與脈動壓力幅頻數據表Tab.1 Data of vibration measuring points and fluctuating pressure amplitude frequency of thrust chamber

從表1 可知,在1 611 Hz、2 884 Hz、4 822 Hz 和9 643 Hz 時,振動徑向測點的幅頻峰值特性與脈動壓力測點的幅頻峰值特性存在耦合關系。軸向和切向振動測點與脈動壓力耦合點較少,由此可以推斷推力室發生高頻橫向聲振。

從上述分析過程可知,采用FFT 分析方法,結合脈動壓力、振動等多類型的動態數據能夠為判斷發動機不穩定燃燒狀態和評價發動機性能提供有力的參考依據。

2.2 小波分析方法

小波分析方法以傅里葉變換為基礎,具有良好的自適應優勢。比利時數學家Ingrid Daubechies 系統總結了上世紀80 年代以來諸多研究人員以及自己對小波的先進研究成果,編寫了文獻[16],對小波分析的基本理論、性質、適用領域和使用規則進行了詳細介紹,使得小波分析成為一門真正的應用學科,并成為國際研究熱點。小波分析在發動機動態數據處理中的應用主要集中在數據去噪、奇異點檢測分析等方面。

符嬈等針對航空發動機轉、靜子發生碰摩時,振動信號頻率產生急劇變化的特點,利用小波分析在局部信息中具有高分辨率的優勢,采用閾值法先對原始含噪振動信號進行去噪處理,再提取有價值信號中的幅值特征和能量信息。通過對試驗數據分析表明,降噪效果較好,能夠準確跟蹤信號中的突變信息[17]。

文壁等重點分析了渦扇發動機起動過程中轉子做功脈動壓力、噪聲脈動壓力、失速團引起的脈動壓力和燃燒波動引起的脈動壓力四種成分,利用小波分析在時頻分析領域的優勢,對含噪信號進行分解,對多次起動過程的頻譜圖,結合起動過程的壓力脈動現象進行分析,結果顯示小波分析方法能夠清晰識別壓力測點不同轉速下的脈動頻率,定位脈動壓力異常的原因[18]。

耿紀洲等運用小波分析和分形算法相結合的方法對發動機軸承磨損的含噪數據進行去噪處理,分析結果顯示該方法能夠清晰提取軸承的故障特征以及判斷最佳的故障診斷部位[19]。

肖云魁等針對小波分析理論中Lipschitz 指數不能清晰定位汽車發動機曲軸軸承工作異常過程中的奇異點和對奇異點能量大小的描述不夠精確的問題,先對試驗數據進行去噪,再采用模極大值多尺度分析方法,對軸承故障數據進行分析。仿真和試驗驗證的結果顯示,該方法能夠精確定位試驗過程中的奇異點位置[20]。

戴屹梅總結了液體火箭發動機渦輪泵低溫軸承研制以及試驗中的性能參數和故障模式特點,介紹了傅里葉變換、小波分析等多種數據分析方法,建立了仿真模型,開發集成了短時傅里葉變換、小波分析等多種方法的數據分析系統,對行業內發動機試驗渦輪泵軸承數據分析提供了重要的參考依據[21]。

楊懿等介紹了小波去噪的基本原理、四種閾值去噪的基本方法以及具體實施的基本步驟。將信噪比作為選擇小波基函數的參考標準,將相關系數作為去噪結果的評價標準。通過對發動機試驗含噪流量數據進行去噪分析,證明小波分析方法能夠有效消除流量數據中的含噪分量[22]。

白泉等介紹了小波分析在實際應用中的基本步驟和方法。小波分析中所用到的小波基函數具有非唯一性,采用不同小波基函數分析同樣的數據時將會產生不同的結果。因此,研究人員列舉了LP 小波、Meyer 小波、Db 小波等多種小波基函數在支撐長度、對稱性和正則性等方面的特征性質,根據小波基函數性質和被分析數據的特征選擇恰當的小波基函數[23]。

采用小波分析方法對某型號發動機試驗關機段推力室脈動壓力數據的奇異點特征進行分析。數據樣本數量為4 000 個,采樣率為10 kHz,選擇DB9 小波小波基函數,分解層數為7 層,分解結果如圖4 所示。

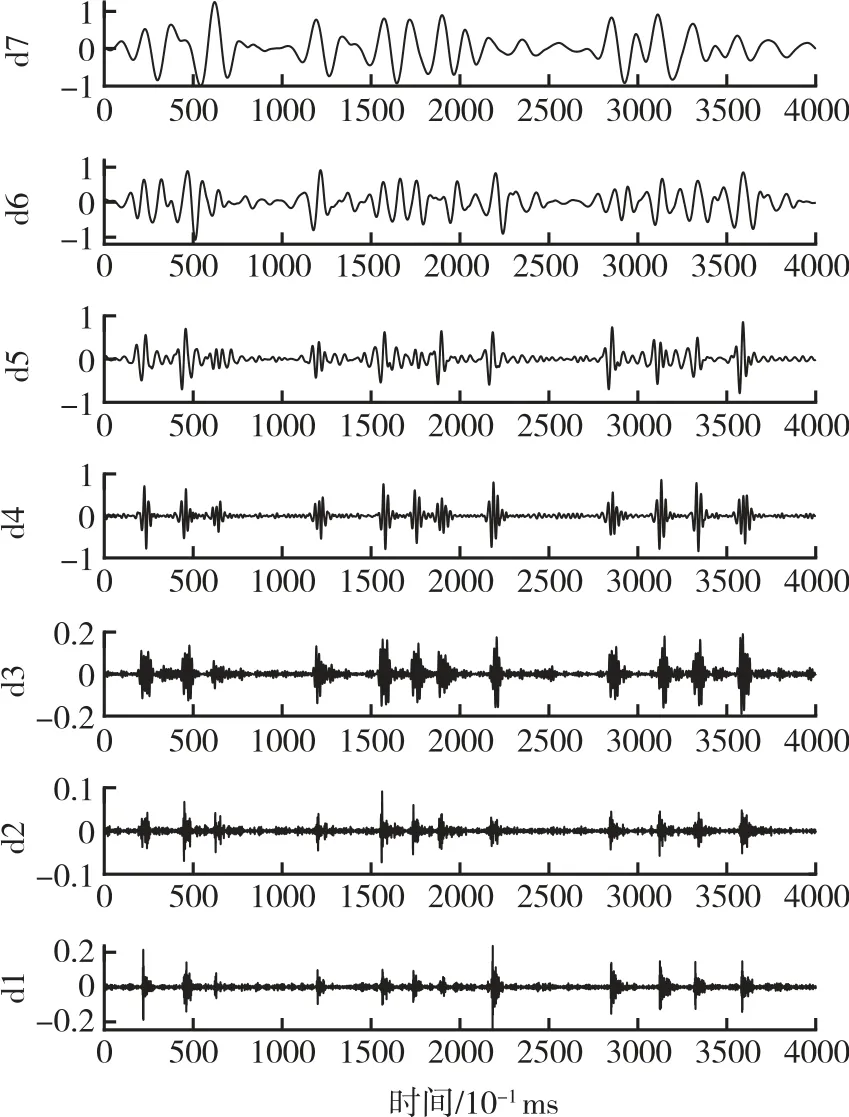
圖4 DB9 小波7 層分解結果Fig.4 DB9 wavelet 7-level decomposition results

對圖4 中d1～d7 的分解結果進行分析可知,小波分析能夠準確定位數據奇異點在時域內的信息。d1～d5 層的分解重構效果較d6～d7 好,能夠清晰觀測到時域內不連續點和幅值變化信息。d1～d4 低層高頻信號中突變能量較d5～d7 層高,包含了原始信號中大部分能量突變成分。隨著分解層數的增加,小波分解過濾的信息較多,d6～d7 層存在一定程度的失真,曲線較為平緩,對分析結果的影響不大。在運用小波分析方法對數據進行分析的過程中,可以將流量、振動等其他數據有效結合,為判斷不穩定燃燒狀態及發動機整體和零部件性能提供重要的參考依據。

2.3 小波包分析方法

小波包分析方法是小波概念的優化和提升。該方法克服了小波變換在中、高頻段頻率局部性分析能力差的缺陷,對信號中的高、低頻部分進行二次分解,從而進一步提高了信號的時頻分辨率[24,25]。小波包分析在信號去噪、奇異點定位、數據壓縮、圖形處理和故障檢測等領域有著廣泛的應用。

楊懿等介紹了小波包分析的基本原理和小波包閾值去噪的基本步驟。在對氫氧火箭發動機試驗流量數據進行去噪過程中,將信噪比和相關系數作為去噪效果的評價標準,取得了良好的去噪效果[26]。

楊懿等采用小波包閾值去噪與分解重構算法分析液體火箭發動機試驗脈動壓力數據。分析了脈動壓力數據在高、低頻段內的系數特征和能量分布情況。結合相應振動測點FFT 頻譜特性對發動機在多個工況內的工作狀態進行分析[27]。

崔建國等針對主燃油泵軸承損壞以及調節器故障引發的喘振問題,將小波包多層分解后的能量信號作為原始信號的特征向量,結合神經網絡中的極限學習算法,建立主燃油泵的故障診斷模型,并將該模型與BP 神經網絡模型進行對比驗證。結果顯示,該模型能夠更加準確、迅速地實現燃油泵故障診斷[28]。

任學平等采用小波包分析方法對汽車發動機運行的含噪振動信號進行去噪處理。根據計算機仿真結果選定合適的小波基函數和分解層數,對降噪后的信號進行殘差分析和統計量分析。降噪結果顯示該方法能有效區分信號中的突變和噪聲成分,具有良好的信噪分離效果[29]。

馬建倉等為有效判斷航空發動機故障類型,統計了5 種常見的航空發動機工作故障特征,將峭度指標、裕度指標、脈沖指標和有效值等時域指標作為評判發動機是否正常工作的參考標準。根據分解結果中高低頻帶的能量信息,繪制多層頻帶的相對能量分布圖,并結合故障特征和時域指標,實現航空發動機故障特征的準確定位[30]。

小波包分析方法在動態數據分析中的使用方法和流程與小波分析基本一致。在采用MATLAB 實現編程分析中,調用的分析程序和基函數稍有不同。

以某型號發動機試驗流量數據為例[26],采用小波包分析方法對含噪流量數據進行去噪分析。樣本點數為8 000 個,數據采集系統采樣率為10 kHz。原始數據如圖5 所示。

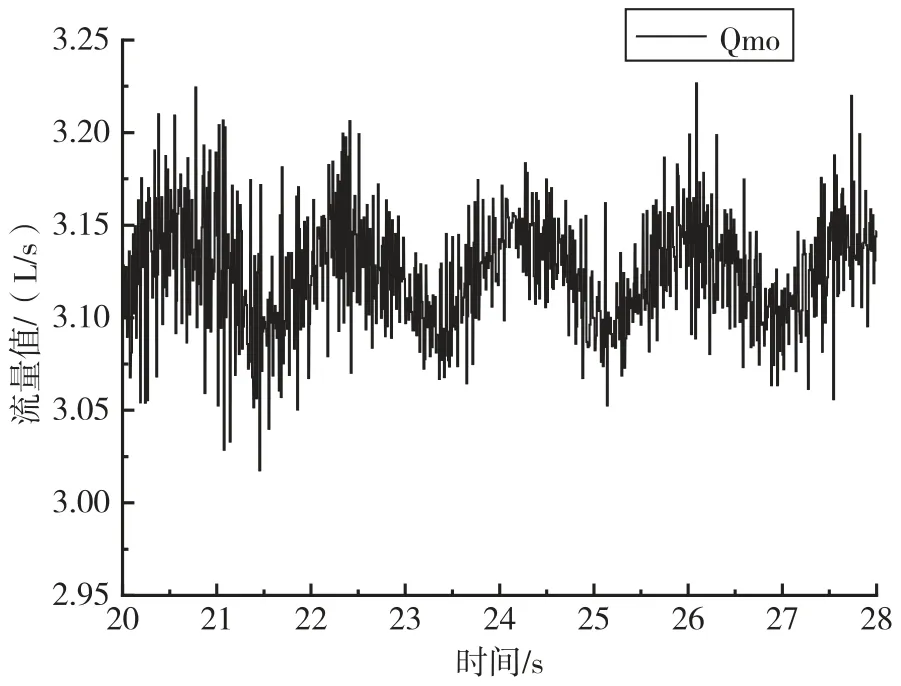
圖5 含噪流量數據圖Fig.5 Noisy flow data chart

分別采用默認閾值法和自選閾值法,對比分析Sym1～Sym9、DB1～DB9 和4～7 層分解結果的信噪比和相關系數的數據,采用Sym6 和Db5 小波基、自選閾值法、5 層分解對含噪數據進行去噪處理,分解結果如圖6 所示。

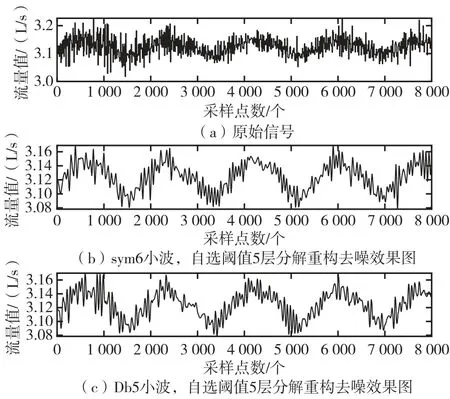
圖6 Sym6 小波和DB5 小波分析結果圖Fig.6 Results of Sym6 wavelet and DB5 wavelet analysis

通過對比兩種小波包分解數據與理論值之間的相對誤差,可以確定更符合實際情況的方法。

2.4 希爾伯特-黃變換分析方法

希爾伯特-黃變換(Hilbert-Huang Transform,HHT)由美籍華人Norden E.Huang 于1998 年提出[31]。HHT 分為兩個部分:經驗模態分解(Empirical Mode Decomposition,EMD)和希爾伯特譜分析。該方法克服了傳統方法中用無意義的諧波分量來表示非平穩信號的缺陷,較高的時頻分辨率和良好的時頻聚集性適用于分析非平穩、非線性數據[32]。

EMD 給出了瞬時頻率的定義,通過引進本征模態函數(Intrinsic Mode Function,IMF)實現非平穩線性信號的平穩化處理,再對IMF 進行希爾伯特變換得到不同特征尺度下的瞬時振幅和瞬時頻率的關系,建立了譜分析與時域的對應關系,能夠精確分析原始信號時頻域的分布規律。但是在運用過程中也存在端點飛翼和模態混疊等問題。近些年來,有諸多研究人員對HHT 使用過程中的問題進行了更加深入的研究,并提出了相應的解決辦法[33-37]。

符嬈等采用HHT 方法從發動機轉子振動信號中提取轉子工作故障信息,并結合振動故障的機理,分析了發動機轉子碰摩的主要特征。MATLAB仿真分析以及發動機試驗轉子振動數據的實例分析證明該方法能夠對信號中的高低頻分量進行分解。分解后的信號清晰顯示了幅頻域內的突變信息以及轉子工作倍頻與幅值的相關信息,為發動機故障定位提供了有力的參考依據。對發動機轉子進行拆解后的分析也印證了該方法的有效性[38]。

李哲洙等采用HHT 分析方法對某型號航空發動機液壓管路不同壓力下的振動信號進行分析,EMD結果顯示該方法能夠過濾信號中的噪聲分量,HHT邊際譜能夠清晰顯示信號中的能量分布情況,為發動機液壓管路的設計提供了重要參考依據[39]。

吳婭輝等針對傳統分析方法無法區分航空發動機高低壓轉子和傳動系統振動數據中多源數據混疊和噪聲分量的問題,采用HHT 方法對混疊振動數據進行分解,借助統計學支持向量機分類方法研究了航空發動機小樣本數據特征,為提取航空發動機故障特征,研判故障類型提供了有效途徑[40]。

楊懿等分析了液體火箭發動機渦輪泵的故障機理,采用HHT 渦輪泵振動數據進行分析。采用信號包絡非閉合鏡像延拓的方法解決了EMD 過程中的端點飛翼的問題。根據Hilbert 能量分布頻譜圖和時頻圖能夠對渦輪泵的故障進行有效診斷和分析[41]。

任剛等提出了一種基于EMD 的改進型變分模態分解方法。該方法將振動信號分解為若干分量,采用結合去趨勢波動分析方法計算各個分量的尺度指數,設定相應的閾值,再對去噪后的分量進行重構。仿真和實測數據證明該方法能夠識別故障信號,消除振動信號的背景噪聲對振動信號的影響和干擾[42]。

高斌分析了希爾伯特-黃變換、小波分析和短時傅里葉變換等幾種方法的優缺點。研究了基于HHT 對轉子和滾動軸承故障進行定位和信息提取,通過EMD 得到各頻率段分量,通過譜分析得到了故障的特征頻率。通過對故障數據特征向量的提取和靈敏度分析,建立基于結構自適應網絡模型,實現轉子和滾動軸承故障的智能診斷[43]。

以某型號發動機試驗穩定段推力室脈動壓力數據為例,采用HHT 方法對數據進行分析。樣本點數為2 000 個,數據采集系統采樣率為10 kHz。4層分解結果如圖7 所示。

分析圖7 可知,EMD 能夠有效提取脈動壓力數據中不同頻率段的信息,圖7(a)～(d)顯示了數據中頻率從高到低的4 個分量,以及數據對應的相對幅值的大小。其中,IMF1～IMF4 階分量在原始信號中所占的比重依次降低。IMF2～IMF4 分量的幅值波動趨勢要大于IMF1 分量的波動趨勢[32]。圖7(e)為信號中存在的無關緩變低頻分量,不影響數據分析。

對IMF1～IMF4 階分量進行Hilbert 變換,變換后的Hilbert 譜分別對應第1 層～第4 層時間-頻率曲線,如圖8 所示。

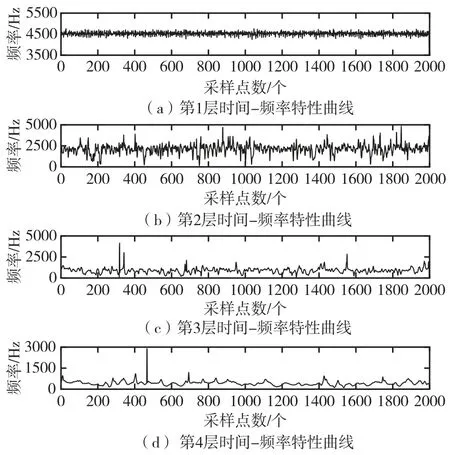
圖8 IMF1～IMF4 時間-頻率曲線圖Fig.8 IMF1～IMF4 time frequency curve

分析圖8 可知,第1 層～第4 層時間-頻率曲線顯示了脈動壓力數據在全時域內的頻率信息。分析第1、2 層時間-頻率曲線,3 500～5 000 Hz 左右的中頻帶所占比重最大,1 500 Hz 以下的低頻帶所占的比重較小。第1 層時間-頻率曲線中,全時域內,頻率變化趨勢較為平穩,沒有明顯的頻率突變點。第2 層～第4 層時間-頻率曲線顯示在全時域內存在多個頻率突變峰值。結合脈動壓力測點上下游對應的溫度、壓力測點、試驗時序和試驗工況等多重信息,為評判發動機燃燒狀態提供重要的參考依據[32]。

2.5 多種方法相結合進行分析的方法

2.1 ～2.4 節介紹了4 種常用的動態數據處理方法,在實際應用中,研究人員可以根據數據的特征和分析方法的優缺點將幾種方法相結合進行數據分析,實現深度挖掘數據信息,提高數據分析的精度和效果的目的。近年來,有多位研究人員就多種方法相結合進行數據分析開展了研究工作。

徐平平等采用小波分析和HHT 相結合的方法對噴嘴腔內自振射流的脈動壓力進行分析,對比了兩種方法在壓力特征信號提取和時頻分析方面的特點,分析結果表明兩種方法在信號分解重構方面都具有自身的特點:小波分析方法能夠較好消除信號中的高頻噪聲分量,但在信號提取方面的能力不如HHT 方法;HHT 方法在信號提取信號特征、消噪和突變點檢測方面更具有優勢[44]。

熊星、蘇濤等針對傳統時頻分析方法的局限性和HHT 在自適應性、完備性和正交性方面的優勢以及HHT 在模態混疊和低頻分析過程中產生內稟函數的問題,將小波分析方法和HHT 方法相結合,分別采用小波分析和HHT 分解依次對信號進行第1、2 層分解、篩選和重構。根據Hilbert 譜和Hilbert邊際譜的分析結果對滾動軸承的故障進行診斷[45,46]。

馬引剛等將HHT 理論中的EMD 方法和獨立成分分析方法相結合,先對火箭發動機多模式組合故障的振動信號進行EMD 分解,得到多個不同尺度下的IMF 函數,再用獨立成分分析方法分離出各振源的獨立響應特征分量。通過實例分析,驗證了該方法能夠從振動數據中有效提取多源振動分量信號特征[47]。

崔建國等為便于提取艦用發動機主泵軸承的振動數據特征,采用小波包分析和支持向量機相結合的分析方法對軸承故障振動數據進行分析。小波包高、低頻段細化分解獲取振動信號的不同故障模式下的能量特征。支持向量機對不同故障特征向量的訓練和分類實現對不同故障的診斷和分析。試驗驗證結果也表明該方法能夠精確識別診斷信號中不同的故障信息[48]。

司景萍等采用小波包分析和人工神經網絡相結合的方法對發動機故障進行有效診斷和分析,建立發動機正常工作和異常故障振動數據庫,采用小波包對振動數據進行分解重構,提取表征發動機工作的特征向量作為神經網絡分析訓練和檢驗的數據樣本,通過神經網絡的訓練,能夠精確識別發動機工作的故障信息[49]。

高遠為提取發動機不同工作狀態的特征信息,采用小波包能量熵和經驗模態分解能量特征分析的方法提取發動機正常工作和故障工作振動信號中的特征向量,再采用支持向量機、分類器和極限學習網絡等人工神經網絡方法,建立不同工作狀態的數據模型。驗證結果表明該方法能夠實現不同工況的識別和分類[50]。

3 結束語

針對發動機動態數據分析處理的實際需求,詳細分析和介紹了FFT、小波分析、小波包分析和HHT 等幾種適用于對發動機振動、脈動壓力等動態數據進行分析處理的方法及其優缺點。介紹了多種方法在實際使用過程中的分析流程,并對試驗數據進行了實例分析。對研究設計人員分析發動機試驗動態數據、挖掘數據信息和優化設計提供了參考依據。