低信噪比下相位編碼信號識別技術

鄧杏松,徐文君,趙榮琦

(中國船舶集團有限公司第七二三研究所,江蘇 揚州 225101)

0 引 言

當今戰場的電磁環境日益復雜,相位編碼、線性調頻等非常規雷達信號不斷增多。雷達信號調制特征識別能夠為雷達信號分選提供有力的幫助,是實現雷達信號識別的重要手段。但是低信噪比情況下非常規雷達信號的特征提取和識別仍然存在問題,這是當前電子戰研究領域的一個重要方向[1]。

目前,很多研究都已對相位編碼信號的識別處理方法進行了研究。文獻[2]采用對信號的瞬時相位或瞬時頻率進行檢測的方法進行相位編碼識別處理,這一方法對信噪比要求很高。文獻[3]通過構造相位跳變點樣本,利用相關處理方法對相位跳變點進行檢測,該方法具有一定的相關處理增益,但改善有限。文獻[4]分析了利用小波變換檢測調制信號的有效性,文獻[5]提出了基于小波模值疊加的碼速率估計方法,驗證了在低信噪比下碼速率估計的有效性。

本文給出了一種基于兩級信道化結構和小波變換的調相信號檢測方法,實現了低信噪比情況下相位編碼信號的檢測。利用信道化提高增益,使用信道化后信道內的零中頻數據進行小波變換,避免檢測相位跳變時的小波尺度盲區,通過檢測小波變換模值的突變點進行相位調制特征識別。最終,將兩級信道化的測量參數進行綜合分析,形成脈沖描述字,保證了各參數的測量精度,提高了信號識別的適應性。

1 兩級信道化設計與實現

信道化接收機是當前常用的滿足電子戰需求的寬帶接收機結構,通過信道劃分,將接收的信號從頻域上分離,具有高頻率分辨率、高靈敏度、能夠處理時域疊加信號等優點[6]。信道化結構通過抑制子信道帶寬外的噪聲提升信號的信噪比。為更好地滿足現代電子戰對接收機高靈敏度的要求,本文設計了一種兩級信道化結構以適應更低的信噪比。以瞬時帶寬500 MHz、中頻960 MHz的設計要求為例,本文以模數(AD)采樣率為1.28 GHz進行兩級信道化設計。

為保證信道化接收機的帶內信號截獲概率,本文采用50%交疊的信道劃分方式,如圖1所示。兩級信道化結構采用串聯方式,第1級信道化輸入為AD采樣的實信號,取信道數32,獨立信道數為16,子帶寬度為40 MHz,理論信噪比增益為12 dB。第2級信道化輸入為第1級信道化選擇的子信道數據。第2級信道化輸入信號有效帶寬為-40 MHz～40 MHz,取信道數8,獨立信道數為8,子信道帶寬為10 MHz,理論信噪比增益為9 dB。

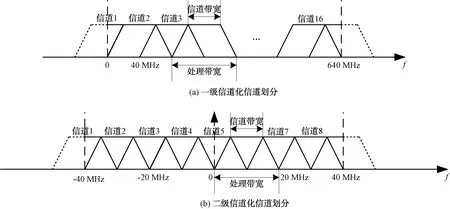
圖1 信道化信道劃分示意圖

本文設計的兩級信道化結構采用系統穩定性好、能實現線性相位的有限長度沖激響應(FIR)濾波器,一級信道化的原型濾波器為192階,二級信道化的原型濾波器為48階,兩級原型濾波器的幅頻響應曲線如圖2所示。

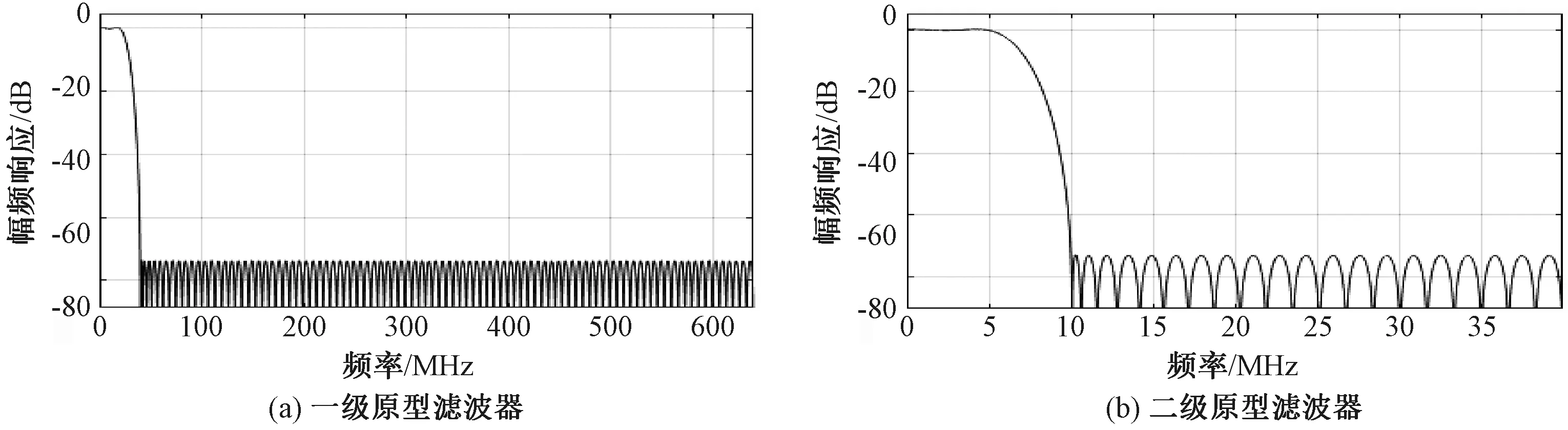
圖2 原型濾波器幅頻響應曲線

本文設計的兩級信道化接收機的信號檢測與處理流程如圖3所示。首先,模數轉換器(ADC)采樣數據經過抽取送入第1級信道化子信道進行參數提取。然后,從第1級信道化子信道輸出的16路信道數據中選取1路信號進行數據處理,同時將該路數據送入第2級信道化子信道進行處理。接著,從第2級信道化子信道數據中選取1路數據進行參數提取,并對選擇的第2級子信道數據進行小波變換,根據小波模值的跳變情況完成調制類型識別,獲取脈內特征。最后,將兩級信道化的測量參數進行綜合分析形成脈沖描述字。

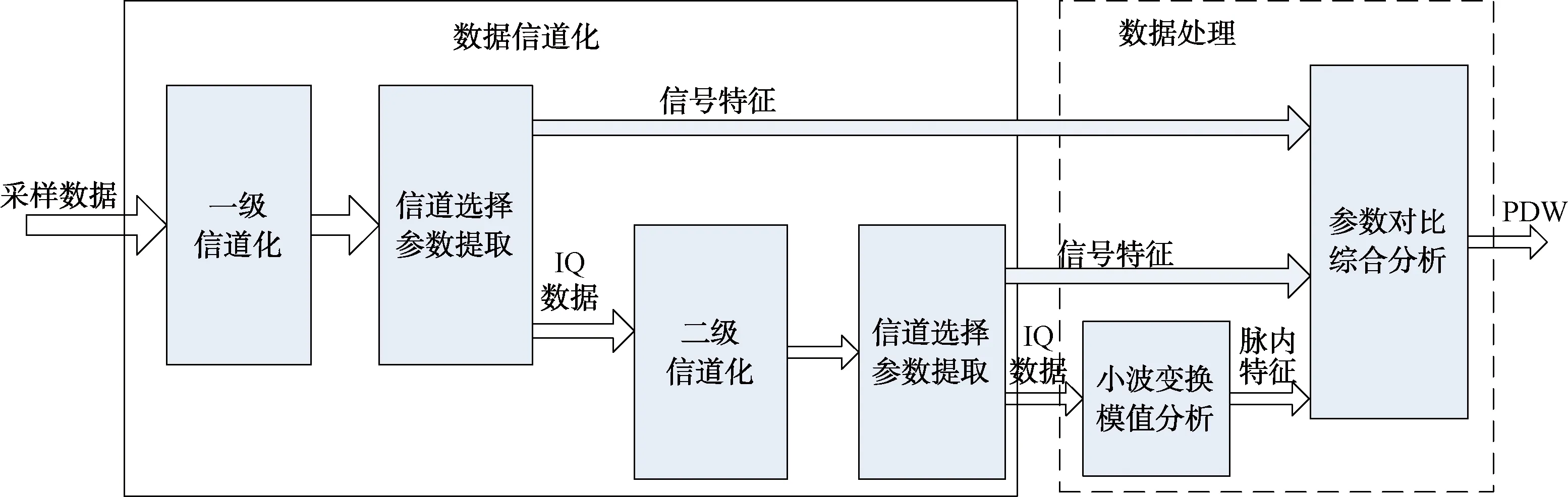
圖3 信號處理流程

2 相位調制信號的檢測和識別方法

小波變換是一種線性時頻變換,是分析非恒定信號和突變信號的有效方法。Haar小波對相位變化的短時信號具有較強的檢測能力,非常適合探測信號的突變成分。文獻[4]詳細給出了使用Haar小波的相位調制信號的小波變換形式。處理相位編碼信號,當Haar小波位于一個碼元周期內部時,小波變換模值為:

(1)

當Haar小波位于碼元跳變點處,小波變換模值為:

(2)

式中:A為信號幅度;T為碼元寬度;wc為信號載波頻率;β為相鄰碼元的相位差。

根據公式(1)可以看出,當小波窗位于碼元周期內時,小波變換的模值是1個與頻率有關的常數;如公式(2)所示,當小波窗位于2個相鄰的碼元之間時,該小波變換的模值出現1個峰值,即表明存在相位變化。因此可以根據小波模值實現信號相位和頻率變化的檢測。

對采樣信號直接進行小波變換時,當wca為2π的整數倍時,公式(1)、(2)中的小波變換的模值為0,峰值消失,根據小波變換的模值無法判斷相位變化,即存在小波尺度盲區。為此,文獻[7]提出在進行小波變換前,將信號由中頻變換為零頻可以消除存在的無效小波尺度。即wc≈0時,公式(1)、(2)可轉換為:

(3)

(4)

當n=iT,小波模值的峰值為:

(5)

公式(5)表明,將信號由中頻轉換為基帶信號后,小波變換的峰值模值主要受小波尺度和碼元間的相位差影響。小波尺度a在不大于碼元周期的范圍內,取值越大,小波模值越大,抗噪聲能力越強;但根據公式(4),小波尺度a取值較大時,時間分辨率降低。本文取小波尺度a=2,以獲得良好的時間精度。

兩級信道化后,子信道內帶寬為10 MHz,遠小于采樣時鐘頻率。根據上述將信號由中頻變換為零頻進行處理的要求,利用兩級信道化后子信道內的數據進行小波變換恰好能滿足小波變換前需要對數據進行頻移的要求,從而避免了可能存在的小波尺度盲區。

3 參數綜合處理流程

采樣數據經過兩級信道化處理后,對各級信道化數據的測量參數進行參數綜合以形成最終的脈沖描述字,綜合分析處理方法如圖4所示。當第1級信道化和第2級信道化數據均存在有效信號時,由于兩級信道化之前都進行了數據抽取,所以第1級信道化的時間測量參數具有更高的時間精度,信號脈寬和到達時間的測量更加準確;當第1級信道化處理結果存在有效信號、第2級信道化結果無有效信號時,表明信號持續時間很短,經過第2級信道化前的數據抽取后,信號無法被正確識別,所以選擇第1級信道化的測量參數作為信號特征;當第1級信道化處理結果無有效信號、第2級信道化結果有有效信號時,表明信號強度較小,需要經過兩級信道化的增益后才能被正確識別,因此選擇第2級信道化的測量參數作為信號特征;當兩級信道化處理結果均未檢出有效信號時,則說明無有效信號。

4 仿真結果與分析

圖5(a)為13位巴克碼(1,1,1,1,1,0,0,1,1,0,1,0,1)調制的二進制相移鍵控(BPSK)信號在0 dB信噪比下的小波變換模值,圖5(b)為13位泰勒四相碼(0,1,2,3,0,3,0,3,0,3,2,1,0)調制的正交相移鍵控(QPSK)信號在3 dB信噪比下的小波變換模值,由上往下依次為采樣數據直接進行小波變換的模值、第1級信道化后子信道數據的小波變換模值、第2級信道化后子信道數據的小波變換模值。圖5表明,在低信噪比條件下,對采樣數據直接進行小波變換,根據小波模值無法進行定位。第1級信道化后子信道數據的小波變換模值在部分位置出現了峰值,但與噪底的模值區分度不高,定位的準確性不高。第2級信道化后子信道數據的小波變換模值有明顯的峰值,且噪底模值較小,能夠進行準確的定位。

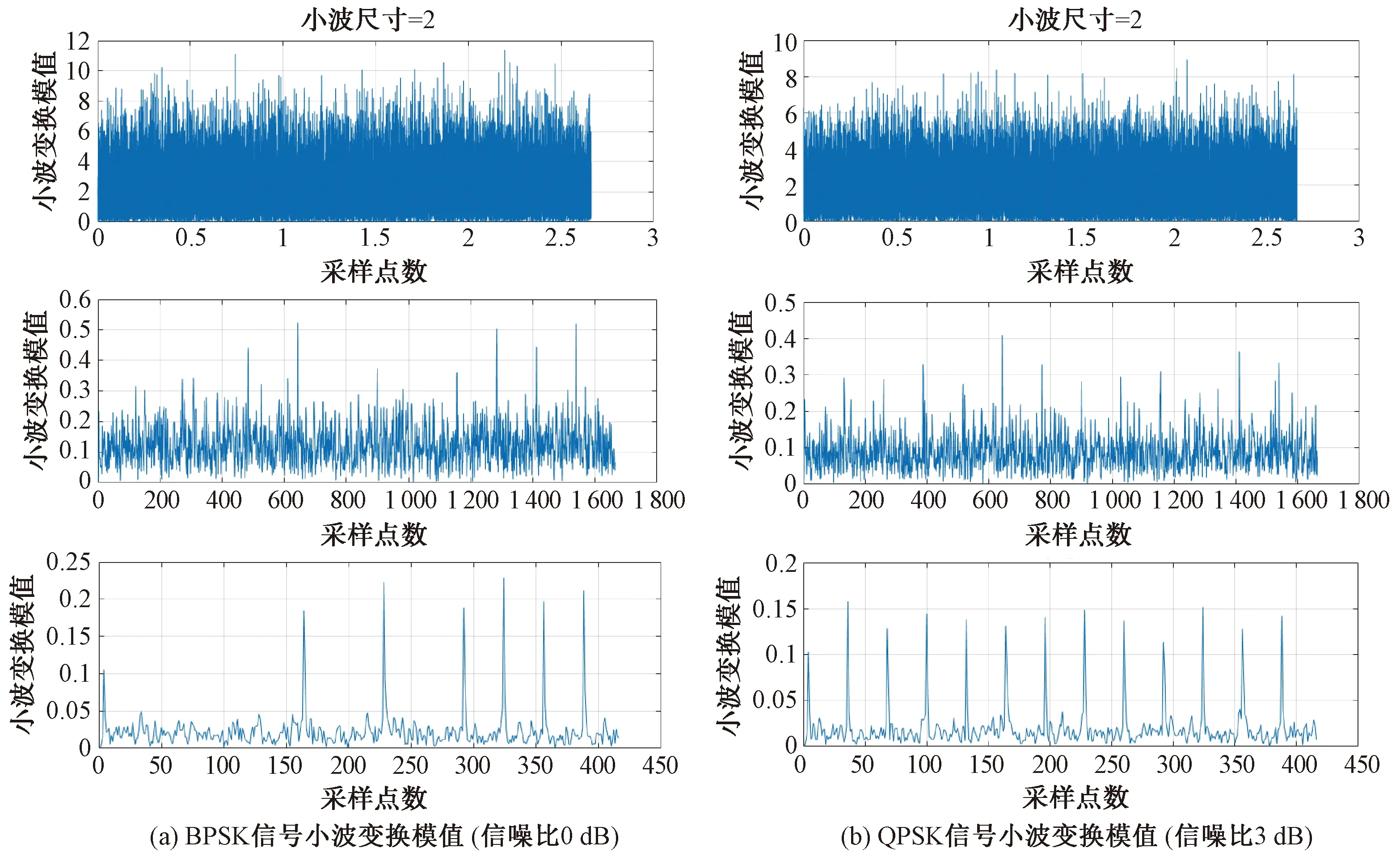
圖5 小波變換模值圖

為考察相位編碼信號識別正確率隨信噪比的變化情況,采用蒙特卡洛仿真法,選擇小波尺度a=2,在各個信噪比下進行仿真試驗,仿真結果如圖6所示。根據BPSK信號識別率仿真曲線,當信噪比不小于-5 dB時,能保證識別正確率達到95%以上。根據QPSK信號識別率仿真曲線,當信噪比不小于-1 dB時,能保證識別正確率達到95 %以上。

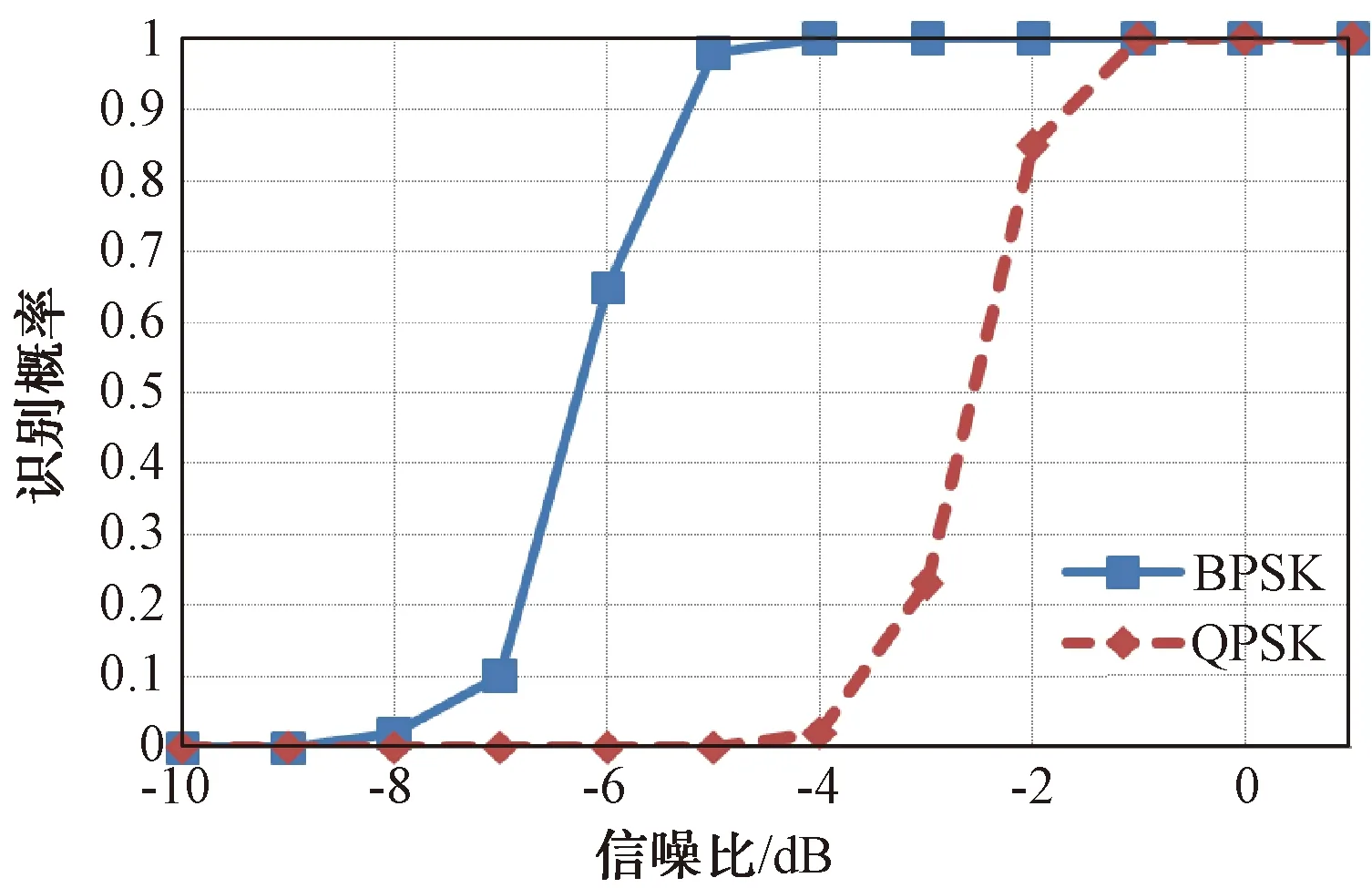
圖6 不同信噪比下調相信號識別率

5 結束語

本文給出了一種基于二級信道化結構和小波變換的相位編碼信號檢測方法,實現了低信噪比情況下相位編碼信號的檢測。利用信道化提高檢測靈敏度的同時,使用信道化后子信道內的零中頻數據進行小波變換,避免了檢測相位跳變時的小波尺度盲區,保證了單一尺度下使用小波變換模值進行相位跳變點檢測的可靠性。仿真結果表明,兩級信道化結構提高了信號檢測的靈敏度,降低了調相信號檢測對信噪比的要求,利用小波變換能夠實現相位編碼信號的正確檢測。本文在數據處理過程中僅選擇單一尺度進行小波變換,后續可以綜合多尺度小波變換的結果進一步提高識別靈敏度和正確率。