“一題多解”與初中數學核心素養培養

曾昭黨

(福建省三明市尤溪縣第五中學,福建 三明 365100)

傳統教學注重對基礎概念、常規解題方法的講解,意在讓學生掌握解題套路,從而應對相關數學題目.然而,初中數學題千變萬化,若學生長期處于被動學習的狀態,使用一成不變的套路解題,勢必會影響學生邏輯推理、數學抽象、數學建模等核心素養的提高.教師應該認識到一題多解教學的必要性,并采取針對性的教學措施在一題多解教學中有效滲透核心素養,在活躍學生解題思維的同時,提高學生的數學解題能力.

1 概念界定

1.1 一題多解

一題多解指的是呈現問題后,學生使用不同的方法解決問題,通過從不同的視角分析問題,培養學生發散思維與創新思維.在教學中,一題多解與一題多變教學存在深入關聯,通過問題變式、問題關聯等方式揭示數學概念、數學算理、數學算法的本質屬性與非本質屬性,從而提升學生的學習層次,開拓學生的解題思路[1].

1.2 數學核心素養

數學核心素養指的是學生在數學學習過程中應具備的關鍵能力,包括數學抽象、邏輯推理、數學建模、數學運算、直觀想象、數據分析六項內容.其中,數學抽象指的是能夠透過數學事物的表面屬性總結出一般規律,并使用數學語言將其表達出來[2].邏輯推理指的是能夠根據數學事實、數學命題按照具體的邏輯規則完成證明命題為真(或假)的能力.數學建模指的是應用數學語言、數學知識、數學方法構建數學模型并解決問題的一種能力,包括分析問題、模型構建等.直觀想象指的是基于幾何直觀、空間想象的基礎上聯想數學事物的形態、變化過程的一種能力,包括圖形描述、數形轉化等.數學運算指的是基于明確的運算題目,按照具體的運算法則完成題目解析的能力,包括運算理解、運算應用等.數據分析指的是基于統計的相關知識分析、推理數據信息,并形成新的結論的一種能力,包括數據收集、數據整理等.

2 基于“一題多解”培養數學核心素養的策略

2.1 設計融合教學目標,奠定素養培養基礎

教學目標是對課堂教學的預設,對組織教學活動、銜接教學環節、填充教學內容具有指導意義.實際教學中,教師根據數學學科核心素養的教學要求融入一題多解的教學過程中,將兩項教學目標融合,設計綜合性的教學目標,為推動一題多解教學順利進行和強化核心素養滲透奠定基礎.目標設計過程中,教師需結合學生的最近發展區設計符合其學習需求的目標,確保教學目標發揮其導向作用[3].

以 “有理數的加減混合運算”這節課的教學為例,首先,教師分析教學目標:①了解代數和的概念;②理解有理數加減法可以相互轉化,會進行加減混合運算;③滲透化歸與轉化思想.然后,教師挖掘解題目標中蘊藏的一題多解教學元素,同時找準教學目標與核心素養培養要求的契合點,如與運算素養、邏輯推理素養、數學抽象素養的契合點等.找準契合點后,教師再融合教學目標,預設一題多解教學思路與教學效果:①布置簡單計算習題,讓學生從有理數加的角度、有理數減的角度分別計算習題答案,激發學生的多解意識,并提升學生的數學運算素養;②布置有理數加減混合運算的應用題,讓學生在解題時提煉有理數信息,并通過不同方式解決問題,使學生掌握多種解法的同時,形成良好的邏輯推理與數據分析素養.教師根據教學目標、教學設計有序組織解題教學活動,能夠進一步提高一題多解的教學效率.

上述案例,通過融合解題教學目標、核心素養培養目標找準一題多解的教學方向,并根據融合目標搭建教學框架,實現了一題多解教學與素養教學融合發展的教學目標,奠定了習題教學順利展開的基礎.

2.2 圍繞問題發散討論,培養學生的邏輯推理素養

初中數學教學過程中,要使學生具備一題多解的能力,首先要解決傳統灌輸式教學造成的學生思維單向、思維僵化問題.針對某一類型題目展開一題多解教學時,教師首先要革新教學觀念,將學生作為習題教學的主體,鼓勵其圍繞問題提出問題,主動與教師、其他學生展開討論.通過組織師生互動、生生互動等多種討論活動,在課堂上發散學生的思維,使其學會從不同角度分析、推理數學問題,在培養學生邏輯推理素養的同時活躍其解題思維.

以 “平行線的性質”一課的解題教學為例,完成基礎知識點的教學后,教師呈現例題:如圖1,已知CD是∠ACB的平分線,DE∥BC,∠B=70°,∠ACB=50°,求∠ADE、∠DEC、∠EDC三個角的度數.這一題目要求∠ADE、∠DEC、∠EDC的度數,需要學生從不同角度分析這一題目,形成不同的解題思路.對此,教師可組織生生討論活動,讓學生以小組為單位結合已掌握知識點、已知信息確定解題思路.比如,有學生結合“兩直線平行,同位角相等”的概念確定圖中∠ADE的度數,解出∠ADE=70°的答案.討論時,學生通過提出自己的見解給其他學生啟發,使學生聯想兩直線平行,同旁內角互補;兩直線平行,內錯角相等的知識,并從不同角度進行推理,確定解題思路.

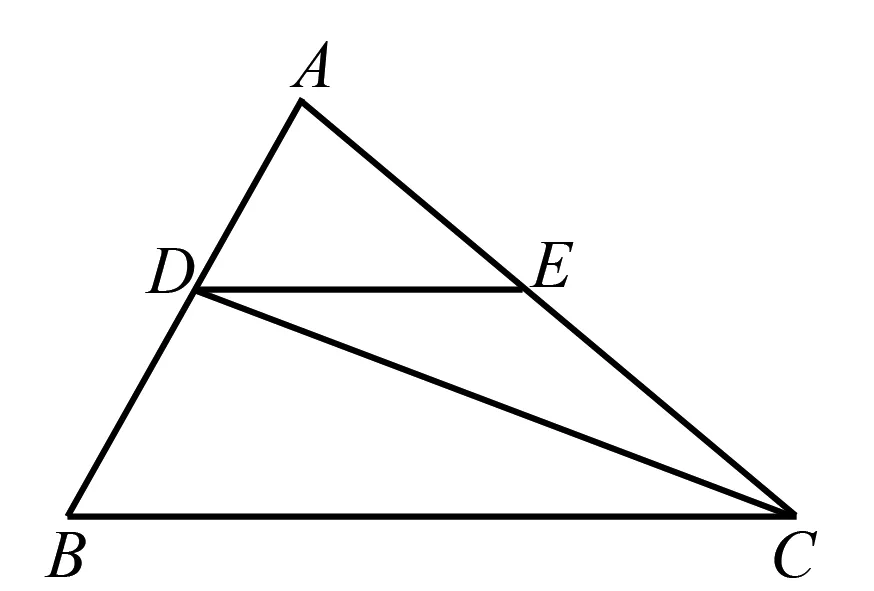
圖1 例題用圖

上述案例,教師圍繞典型例題組織生生討論活動,讓學生結合已掌握的知識點提出看法,以拋磚引玉的形式啟發學生的一題多解思維,在廣泛交流、深度思考的過程中發散學生的解題思維,提升學生的邏輯推理素養.

2.3 圍繞問題對比分析,培養學生的數學抽象素養

一題多解的教學目的并非“多解”,而在于培養學生多角度、多層次、多方位思考問題、探究問題的解題思維.教師在展開一題多解教學時,應拓寬教學思路,將圍繞著某一題目的多種解法教學轉向類型題的分析教學,使學生明確不同題目的異同處,題目中條件與結論的內在關聯,使學生掌握從不同角度探究問題的方法[4].對此,教師有必要在解題教學中進行對比分析教學,使學生在題目對比的過程中總結規律,進一步培養學生的數學抽象素養.

上述案例,教師結合教學內容的考點呈現多種類型題,讓學生通過對比分析探究解題本質,既提升了學生解題思維的靈活性,又提升了學生的抽象素養.

2.4 圍繞例題展開變式,培養學生的數學運算素養

要真正擺脫解題方法單一的問題,使學生能夠全面的、多角度地探究數學問題,需要教師圍繞典型例題展開變式教學.在學生掌握問題的常規解法后,組織學生從其他角度探索問題的解決方法,使學生認識到問題解法的不唯一性,增強其靈活應變的解題意識.基于此,教師再出示類型變式題,讓學生在讀題、解題、運算的過程中總結一題多解的經驗,同時提升其數學運算素養.

2.5 應用導圖總結方法,培養學生的數學直觀素養

思維導圖是一種直觀、有效的思維教學工具,將其應用到初中數學的一題多解教學,可以使學生的解題思維更加清晰、直觀,有助于在解題教學中培養學生的數學直觀素養.應用導圖時,教師可將待解決的數學題目作為導圖的錨點,圍繞問題搭建多解框架,組織學生將不同解題思路填充到思維導圖的結構框圖上,并總結這一方法的優缺點[5].這樣,學生能夠充分掌握題目的不同解法,一題多解的能力得到增強.

以“一元二次方程的應用”一課的教學為例,教師出示典型例題:制造一種產品,原來每件的成本是120元,由于連續兩次降低成本,現在成本為78元,求平均每次降低成本百分之幾?圍繞這一問題設計思維導圖,讓學生將題目的已知量與未知量、列方程解應用題的步驟、解方程的方法(配方法、公式法、因式分解法)等內容填充到思維導圖上.借助思維導圖直觀呈現不同解題方法及其解題依據,進一步強化一題多解教學效果.

綜上所述,初中數學一題多解教學與核心素養培養教學存在教學關聯,融合兩項教學工作對于提升初中學生的數學綜合素養有著積極意義.實際教學中,教師應充分理解一題多解、數學核心素養的教學內涵,同時根據初中學生的認知發展規律采取多樣化的解題教學方法,使學生在獨立思考、綜合討論、對比分析的學習過程中形成靈活的解題思維,進一步提升學生的數學核心素養.