基于多智能體的被裝精準申領庫存策略仿真研究*

史博元 董 鵬 鄭麗莎 文昊林

（海軍工程大學 武漢 430000）

1 引言

2018 年8 月，我軍在全軍72 個單位進行“精準申領”試點工作，經過兩年時間的探索與改進，2021年，軍委后勤部與多家地方物流公司簽訂戰略合作協議，以戰區為保障單位建立軍民融合倉庫，利用地方物流公司成熟的技術與經驗，加速被裝運輸鏈路的“最后一公里”，同年4 月21 日，在全軍范圍內正式推廣被裝的“精準申領”保障模式［1］。不同的是，試點期間每年兩次的“定期申領”升級成了“隨時申領”：官兵可以在任意時間登錄平臺申領被裝，并且可以實現十天內送達，極大地提高了被裝保障效率。

在我軍以往的被裝實物供應模式中，長期存在著差異化需求難以滿足、保障精確性不高、閑置浪費等問題，而被裝精確申領模式很大程度上解決了上述問題，邁出了保障能力提升的關鍵一步［2］。但由于這種供應保障模式推行的時間較短，目前仍處于探索階段，在供應鏈效費比方面還存在一定的不足，例如各節點庫存控制策略不夠精準，導致部分被裝庫存長期缺貨或積壓。本文在現有的庫存控制策略基礎上，利用anylogic仿真，對其存在的問題進行改進，以期實現提高效率、降低成本、減少浪費的目標。

2 策略分析

2.1 現狀分析

目前，被裝精確申領的供應鏈主要分為四個節點，分別是軍需物資供應商（下稱工廠）、軍需物資倉庫（下稱軍需倉庫），配送服務供應商（下稱物流公司）和部隊用戶，供應鏈中最常見的保障模式如圖1 所示。首先，由軍委后勤保障部定期匯總申領平臺中的官兵需求信息，將其與軍需倉庫和工廠的庫存進行匯總對接后，調配物資并開展下一個周期的采購，工廠根據訂單，將被裝送達軍需倉庫；而后，倉庫將調配完畢的被裝，送至軍民融合倉庫；最后由物流公司進行相應的分揀后，配送至部隊用戶［3］。這種庫存控制策略對每個周期采購量預測的準確性依賴較大，但由于精準申領模式運行時間較短，可參考數據較少，加之新冠疫情的影響，難免會出現需求和產能兩方面的波動，造成某些被裝長期缺貨，影響保障效率和質量，或者庫存嚴重積壓，浪費大量的庫存成本。考慮到配送階段由地方物流中心負責，本文只研究工廠和軍需倉庫的庫存策略，著重從軍方層面入手，降低成本、提高效率。

圖1 常見供應鏈保障模式

2.2 軍需倉庫庫存策略設計

本文采用的原始數據，來源于實行精準申領一年內中部戰區Z 倉庫某被裝的庫存量和需求量，去除起始階段訂單量暴增導致的極端數據，最終選取的時間范圍為2021年5月7日至2022年4月21日，庫存狀態折線圖如圖2所示。

圖2 庫存狀態折線圖

數據顯示，庫存波動范圍較大且水平整體偏高，產生大量的庫存成本。針對庫存策略的不足，進行改進并利用anylogic軟件進行建模仿真。軍需倉庫庫存狀態圖設計如圖3所示。

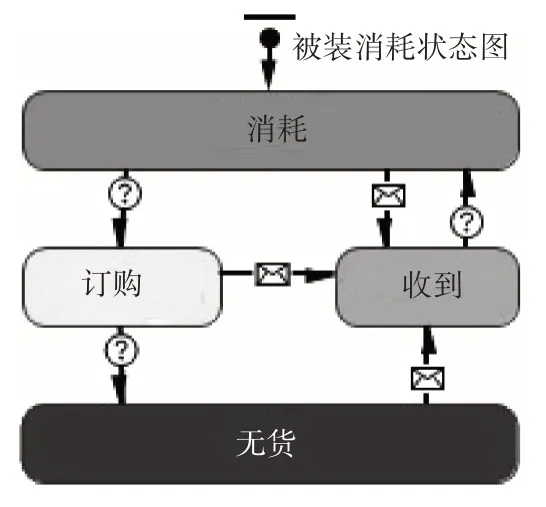
圖3 軍需倉庫庫存狀態設計圖

其庫存策略及參數設計如下［5］：

1）庫存閾值S：當軍需倉庫某型被裝庫存低于該數值時會向工廠訂購產品。

2）訂購批量P：每次向工廠訂購的批量。

4）工廠要求的最小訂購批量M。

由于每次訂購產生的額外成本較低，可以忽略不計，因此根據經典EOQ 理論，通過降低訂購批量可以達到降低成本的目的［4］；另外，在可預見的未來，國內新冠疫情形勢仍不容樂觀，原料斷供和工廠停產依舊會是常態，無疑將對生產和庫存造成巨大影響。綜合各種影響因素，應該盡量減少單次的采購批量，增加采購次數，降低成本的同時，將不確定性事件的影響降至最低［6］，但是采購量還需要滿足下列約束條件：

1）在采購期內滿足最大需求。該最大需求可作為發起采購的時機，即庫存閾值S。

2）滿足下一個訂購期的需求。若訂購批量較小，在貨物運輸到倉庫時庫存可能無法滿足需求，因此考慮最極端的情況，即每日都消耗最高的數量，即可推算出訂購批量P。

3）采購量過低會急劇提高單位制造成本，所以采購批量要滿足工廠的最小訂購批量。

通過模擬仿真，得到的直接數據有：

1）fx：在x天內產品需求統計數據集，x為整數，max(fx)表示在x天內最大的需求量。

2）Fx：在x天內產品需求積累情況，x為整數。

對此，根據仿真系統計算出的多日需求統計數據，設計了以下幾種庫存策略。

若只考慮T 日內的需求情況，易得庫存閾值S應為max(f)，這樣的庫存閾值能夠保證庫存在天的時間內不會耗盡。考慮每個周期的需求量最大都為max()時為極限情況，天后的庫存又會小于庫存閾值，同時會發起第二次訂貨請求，此時訂購批量P應為

通過仿真系統將參數帶入，得到軍需倉庫庫存變化情況，如圖4所示。

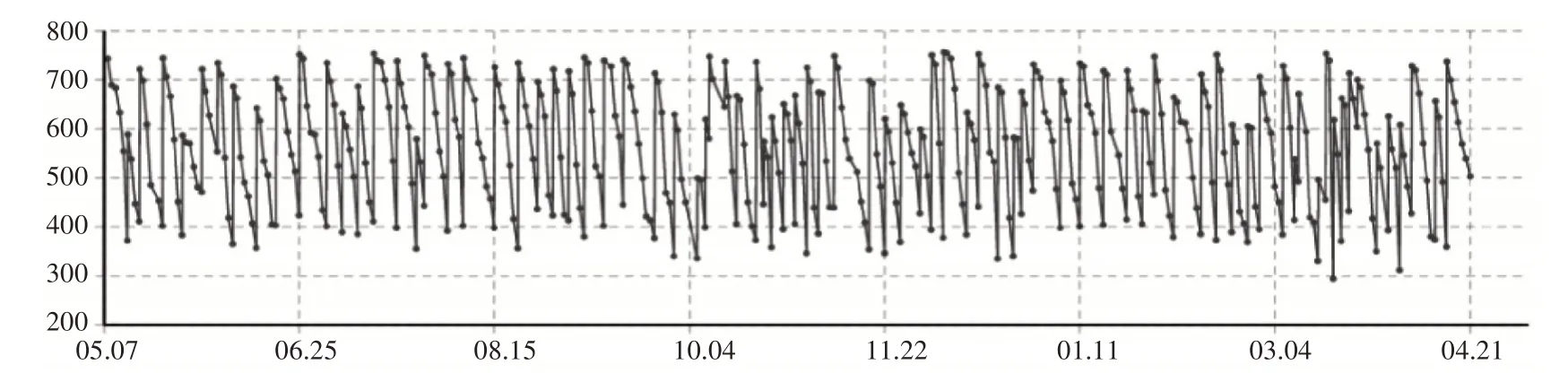
圖4 軍需倉庫庫存變化情況

分析圖中數據可以得出，該庫存策略雖然滿足了全部需求，但整體庫存仍維持較高水平，不夠合理，這是由于現實中很少出現相鄰幾天需求都達到最大的情況，因此，還需對該策略進行進一步的優化。

在上述訂購批量P 的條件下，可能會導致缺貨，所以還需對訂購批量進行修正：

通過仿真系統將參數帶入，得到軍需倉庫庫存變化情況，如圖5所示。

圖5 軍需倉庫庫存變化情況

圖中最低庫存水平沒有趨近0，這是由于同時滿足庫存數量最低，且剛好遇到最大需求的概率較低，因此該方案比較符合實際情況。但方案也存在一些問題，考慮到部分被裝的季節性特點，大部分情況下庫存水平維持較高，只有一些特定月份需求較大，因此還可以通過考慮特殊時期進一步對庫存方案進行設計［7］，具體見2.2.3節。

2.2.3 按月規劃庫存策略

在前兩種設計方案的基礎上，設計按月規劃庫存的策略，原因在于考慮到了被裝的季節性特點，目的是為解決因季節需求差異而導致的總體庫存偏高的問題。以某型被裝為例，通過分析該被裝的適用季節及往年數據，發現在3 月及10 月，訂單需求會有較大的增加。因此，只需使用2日需求分析的方法將每月的庫存策略區分處理即可。對庫存策略按月區分規劃，得到庫存變化如圖6 所示，倉庫根據歷史需求信息和季節變化調整庫存策略，從而能夠達到降低庫存成本的目的［8］。

圖6 軍需倉庫庫存變化情況

2.3 工廠庫存及生產策略設計

相比軍需倉庫，工廠的庫存數量與被裝產量有直接關系，因此還需要同步設計其生產策略。工廠的庫存狀態圖設計如圖7所示。

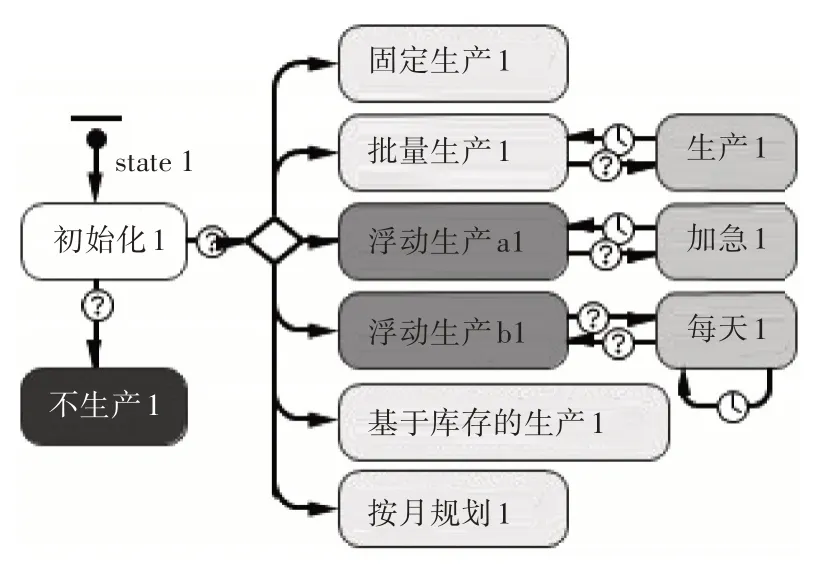
圖7 工廠庫存狀態設計圖

其庫存及生產策略參數設計如下［9］：

1）每日生產R：每天生產固定數量的產品。

2）庫存閾值S：當產品庫存低于該數值時會進行加急生產。

3）生產批量P：加急生產的批量。

4）生產周期T：被裝從生產、入庫到最后出庫的時間，單位為天。

通過模擬仿真，得到的直接數據如下：

1）fx：x天內產品需求統計數據集，x為整數，max(fx)表示在x天內最大的需求量。

2）Fx：從第1 天到第x天產品需求積累的情況，x為整數。

根據仿真系統計算出的多日需求統計數據，設計了以下幾種生產策略。

2.3.1 固定生產策略

在該策略下工廠每天只生產固定數量的產品R，不進行加急生產，使得全年都可滿足需求。所以為維持每年的總體需求，每日產量R 為，得出工廠庫存變化曲線如圖8所示。

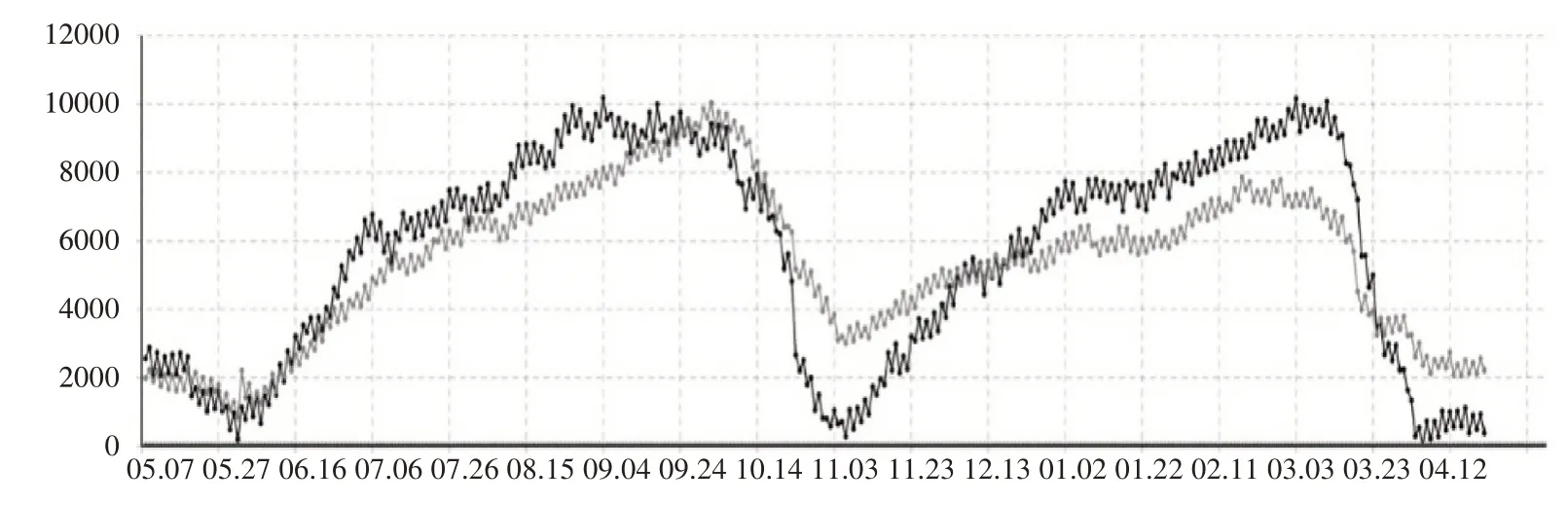
圖8 工廠庫存變化情況

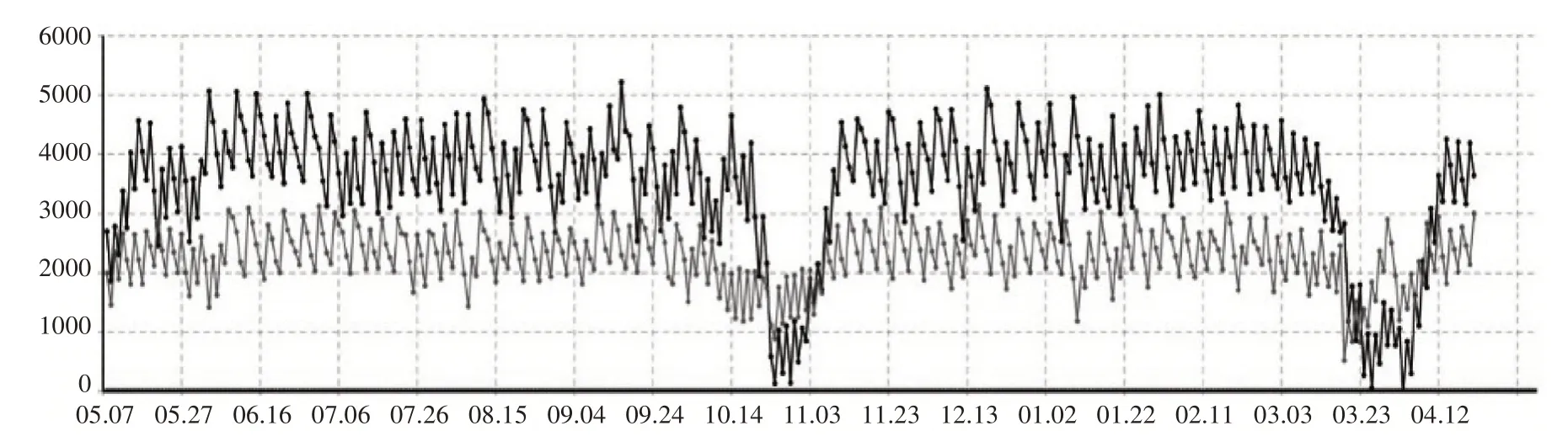
圖9 工廠庫存變化情況

由圖8 可以看出，由于設定了較高的每日生產數量，庫存水平會有一段時間的積壓，維持在較高水平，且該策略需要比較合適的初始庫存，不太符合實際情況。

2.3.2 批量生產策略

該策略類似于軍需倉庫庫存策略的設計，在該策略中，每日固定生產量為0，當庫存低于某一閾值時才開始生產。特點是工廠在低庫存時生產固定的量后停工，但這種策略需要高庫存水平以應對風險，且每日生產波動較大。

將參數帶入仿真系統，得到工廠庫存變化情況示意圖如下所示：

2.3.3 二級生產策略

為了使每天生產數量波動變小，同時避免較高的庫存水平，應結合2.3.1 節與2.3.2 節中的方案設計新的策略：工廠每天生產固定數量R 的產品，當庫存低于某一閾值S 時，每天加急生產P 件產品，在生產時間T 天后交付。在這種生產策略下，生產批量分為兩級：高庫存時每天生產R 件產品，低庫存時每天生產R+P 件產品。通過每日的固定生產滿足部分需求，同時降低了高需求時的波動水平［10］。這種策略中的加急生產數量相對于前一種策略更少，生產波動更平緩，但會造成高水平庫存的延遲，且生產時間越長，延遲增長越高。采用OptQuest Engine 智能優化引擎，進行500 次迭代，得到的庫存變化曲線如圖10所示。

圖10 庫存變化情況

對比2.3.2 節中的數據，顯然2.3.3 節中的策略生產數量的波動更小，且庫存水平較低。對這種二級生產策略進行擴展，可以得到基于庫存數量的生產策略，具體見2.3.4節。

2.3.4 基于庫存數量的生產策略

在該策略下，輸入數據為每日產品的需求量和生產時間，輸出策略為生產數量關于產品需求量的表函數，也可以稱之為多級庫存控制策略，總體方法是將產品需求分布轉換成生產數量與庫存數量的關系［11］。設生產時間為T，每日產品需求量分布為f1。該策略的目標是使最低庫存不下降到0 以下，且平均庫存數量最低。在此策略下需要設計若干個控制點，其中橫坐標為庫存數量，縱坐標為該庫存數量下應生產的產品數量，由此可以構建一個表函數，再使用插值計算［1］，形成圖像，將2.3.3節中的二級生產策略用這種方式表示如圖11所示。

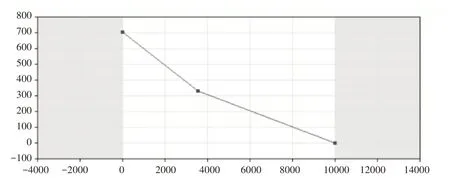
圖11 改進后的生產策略

2.3.5 按月規劃的生產策略

研究需求發現3月和10月訂單數目會激增，可結合以上所有策略設計不同月份的庫存策略參數。由于篇幅所限，在此不再展示仿真結果。

3 結語

被裝精確申領模式是我軍后勤保障歷史上的一次重大突破，其質效直接關系到官兵的切身利益，意義重大，影響深遠。本文針對申領模式供應鏈中存在的庫存問題，提出相應的改進方法，并利用anylogic軟件，對庫存策略的效果進行模擬仿真，仿真結果表明，該方法對于提高效率和降低成本作用比較明顯，可以為相關部門的策略制定提供一定的思路。