基于貝葉斯網絡的艦機協同動態結果預測研究*

張財生 司沈闖

（1.海軍航空大學209教研室 煙臺 264001）（2.中國人民解放軍91856部隊 上海 201900）

1 引言

在預警機、艦載雷達等探測裝備發現目標后，編隊指揮官需要決定是否對其進行攻擊，以及攻擊結束后是否要進行二次攻擊。由于航母戰中參戰單位數量龐大，指揮協同復雜，戰場態勢瞬息萬變，如果戰略決策僅依靠指揮官的個人經驗，那顯然是不夠的。因此，需要開展動態過程預測，預測戰爭走向和己方的獲勝概率，輔助編隊指揮官在復雜的戰場環境下迅速定下作戰決心。而動態過程預測的結果是編隊指揮官進行指揮決策的重要依據，能夠輔助指揮官及時定下正確的戰場決策。建立動態過程預測仿真模型是一個復雜的過程，但需要考慮的問題主要有以下三點：

1）正確選擇模型的特征量：戰場上的戰爭要素有很多，在模型里無法全部體現出來，因此要重點地選擇幾個有關鍵性作用的變量進行分析，特征量的選取要合理且要容易獲取。

2）模型要有良好的實時性與動態性。現代海上戰場信息化程度較高，分分秒秒的時間延誤都會影響作戰的效果，因此該仿真模型進行動態過程預測的實時性要高，并要能體現出戰爭是一個動態變化的過程。

3）模型要有一定的可靠性。現代戰爭是一個大量使用高精尖武器的信息化戰爭，指揮員一旦決策失誤，將使整個編隊遭受毀滅性打擊，因此動態過程預測結果要盡量準確，這樣為戰場指揮員提供的決策方案才能更加可信。

在預測類似于戰場勝負等不確定性較大的問題上，眾多學者前后提出了諸多不同的建模理論［1～3］，其中貝葉斯理論［4］在結論可靠性上具有明顯的優勢。貝葉斯理論的基礎是概率論，主要是通過貝葉斯網絡和條件概率公式解決事情因果依賴比較明顯的問題，因此使用貝葉斯理論對艦機協同作戰中的動態過程和結果進行預測更加合理。本文針對預警機支援下的艦機協同動態過程中的結果預測問題，以雙方戰機之間的攻防作戰為研究背景，選取作戰中的特征變量，然后根據特征變量構建貝葉斯網絡，確定各節點條件分布概率，最后通過模擬貝葉斯網絡的Netica軟件進行仿真分析。

2 貝葉斯網絡模型分析

貝葉斯網絡模型中有兩類不同的節點［5］，分別稱作觀測節點和隱藏節點。觀測節點是指建模時選擇的具有代表性的變量，即特征量，這些變量可以從戰場中直接觀測獲得；隱藏節點無法通過觀測獲得，而是需要根據觀測節點的實時狀態依照相應原則推導計算得到。

如圖1 所示，在實際作戰中，“紅方防御能力”和“紅方機動能力”將會直接影響“紅方毀傷程度”。其中，“紅方防御能力”和“紅方機動能力”為觀測節點，是預定的特征量，在作戰中可直接通過觀測獲得；“紅方毀傷程度”為隱藏節點，其狀態分布需通過計算獲得。

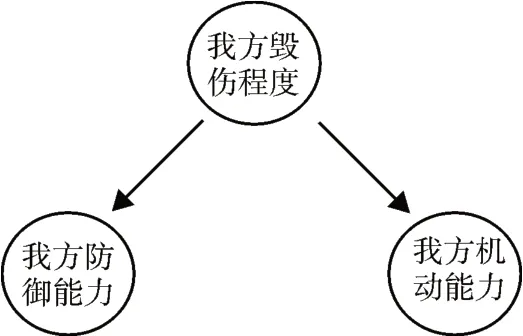
圖1 貝葉斯網絡模型示意圖

貝葉斯公式用于貝葉斯網絡的計算，而貝葉斯公式又是由條件概率公式推廣而來的，可知貝葉斯模型結構能定性地表現節點之間的因果關系，條件概率可以定量地計算節點間的關聯程度，因此在貝葉斯網絡中的各觀測節點要設置關于隱藏節點的條件概率，該貝葉斯網絡才能按特定的流程進行概率計算。在圖1 的示例中，“紅方毀傷程度”的條件概率如表1所示。

表1 毀傷程度條件概率示意表

可以看出，在毀傷程度為輕損的條件下，紅方單位的防御能力為優、良的概率分別為0.8、0.2，機動能力為強、弱的概率分別為0.7、0.3，這個概率可以理解為在當前狀態下，紅方有80%的作戰單位防御能力為優，20%為良，機動能力70%為強，30%為弱；在總體毀傷程度為重創的條件下，紅方單位的防御能力為優、良的概率分別為0.1、0.9，機動能力為強、弱的概率分別為0.2、0.8，可以理解為紅方有10%的單位的防御能力為優，90%為良，機動能力有20%為強，80%為弱。在實際作戰中，可以根據當前態勢實時觀測更新“紅方防御能力”和“紅方機動能力”這兩個觀測節點的狀態，利用節點間的條件概率，進而反向推理出“紅方毀傷程度”的狀態分布。

3 動態過程預測建模

通過對貝葉斯網絡的分析，得出利用貝葉斯網絡進行動態過程預測的建模流程［6］，如圖2所示。

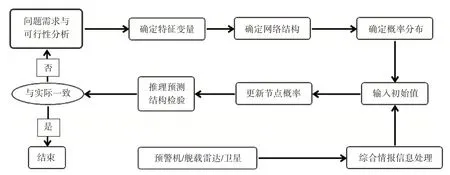
圖2 動態過程預測建模流程

圖2 中的流程關系可進一步總結為以下四個步驟。

1）確定特征變量

為了便于分析，本節確定以下七個變量作為戰機與戰機作戰時的特征變量：導彈性能、飛機數量、導彈命中率、機動性、防御能力、毀傷程度及預警機性能。

2）構建貝葉斯網絡

不同特征變量對結果有不同的影響，需要根據已經確定特征變量建立一個能反映因果關系的貝葉斯網絡。目前大多數學者在利用貝葉斯網絡進行動態過程預測時都沒有考慮時間因素，即在一開始就根據雙方的裝備性能等數據直接給出戰斗結果，沒有考慮戰場的動態過程。

3）確定節點概率

貝葉斯網絡是由各種節點和關聯線組成的，所有的子節點都要設置與其對應父節點的條件概率，表示兩者的相關程度，這個條件概率應當由專家確定，或者在取得大量數據后進行數學統計得出。

4）使用Netica軟件進行建模仿真

依照構建的貝葉斯網絡使用Netica 軟件設置節點、關聯線、條件概率等。在戰爭開始前，預警機的信息處理系統會從搜集到的戰場信息中檢索出需要的特征量，接著將其當前狀態及時輸入到觀測點中，并實時調整網絡的觀測節點狀態。仿真通過更新不同時刻的特征量，反映戰斗中時間的演化過程，仿真結果會比傳統的靜態貝葉斯網絡的預測結果可靠性更高。

4 仿真分析

4.1 仿真背景描述

為了簡化問題，本節仿真僅對兩軍艦載戰斗機之間的勝負做出預測。假設兩軍的戰機性能類似，即紅方戰機的攻擊能力和防御能力與藍方相同，掛載導彈性能相近，戰機毀傷程度、導彈命中率的條件概率分布也相差不大。戰場動態過程預測［7］的貝葉斯網絡模型如圖3 所示，其中“預留”接口的作用主要是為模型擴展升級預留。

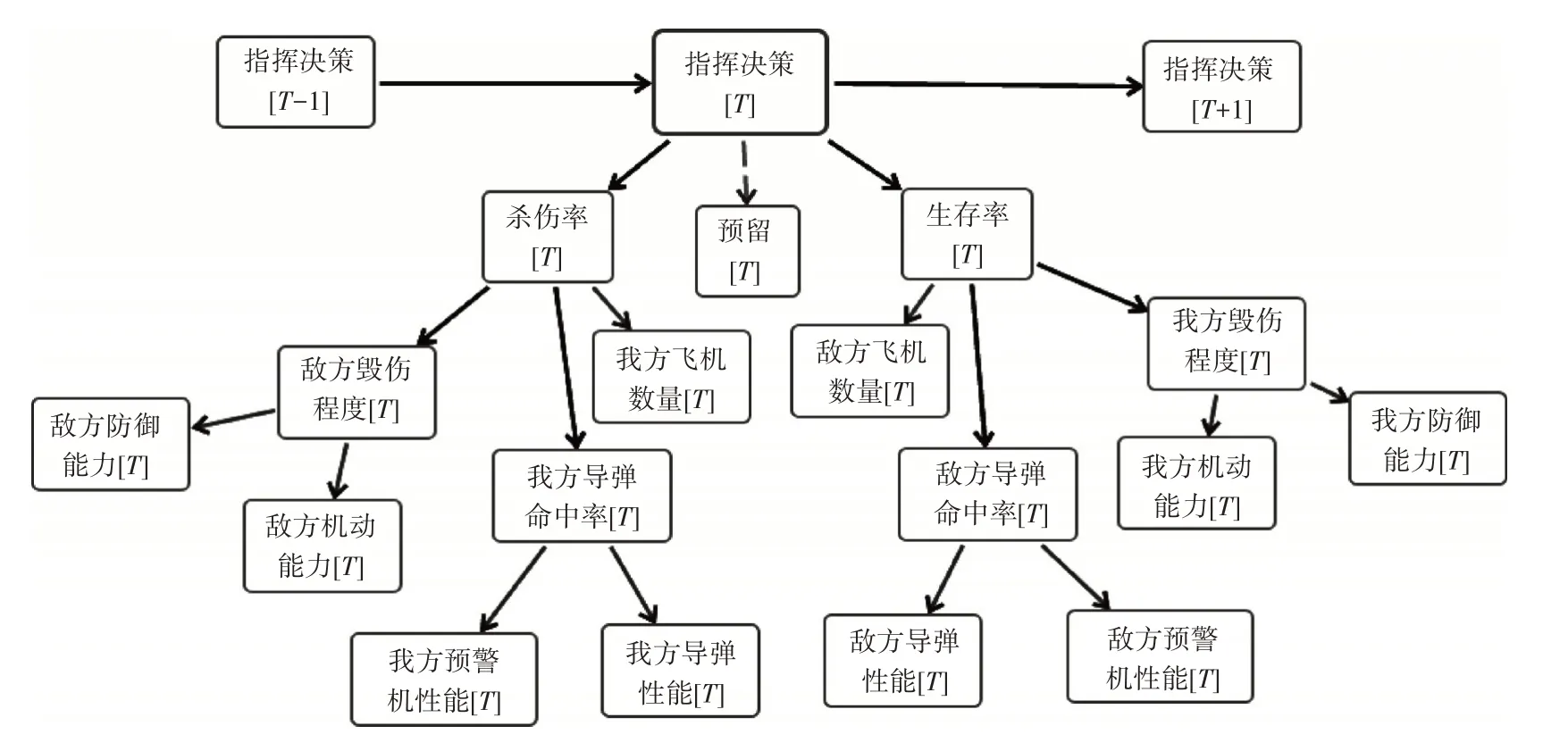
圖3 戰場動態過程預測貝葉斯網絡結構圖

在該網絡模型中，每個觀測節點的狀態如下：飛機數量為多、中、少；防御能力為強、中、弱；機動性為好、中、差；預警機性能為優、良；導彈性能為優、良。設定每個隱藏節點的狀態值如下：導彈命中率為高、中、低；毀傷程度為無損、輕損、輕微、摧毀；殺傷率為高、中、低；生存率為高、中、低；指揮決策為攻擊、規避。毀傷程度包括無損、輕損、重創、摧毀，其中摧毀代表完全失去戰斗能力。

4.2 參數選定

由于建立模型時所設定的雙方飛機性能大致相同，因此以下條件概率分布不分紅藍雙方。

1）導彈自身的性能以及預警機制導能力的強弱對命中率有重大影響，本示例確定導彈命中率的條件概率如表2所示。

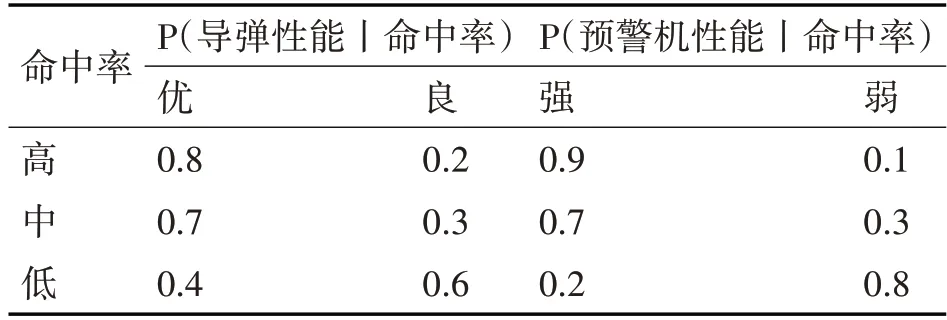
表2 命中率的條件概率表

2）飛機的毀傷程度直接影響到該飛機的防御能力和機動能力，本示例確定飛機毀傷程度的條件概率如表3所示。

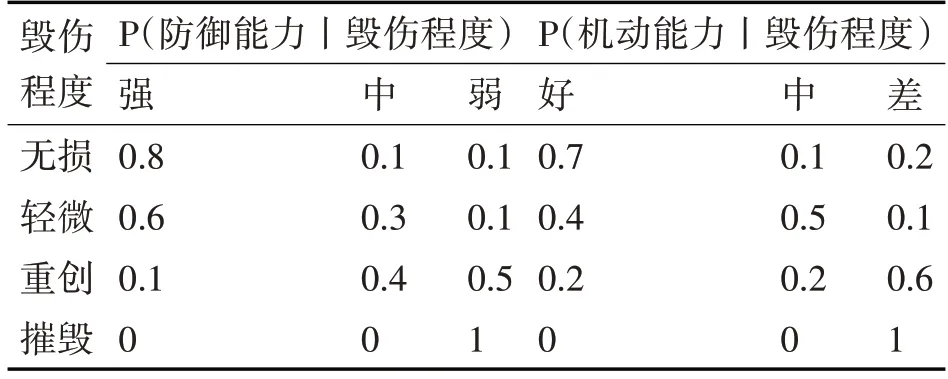
表3 毀傷程度的條件概率表

3）雙方的飛機數量、導彈命中率和毀傷程度都會影響紅方的生存率和殺傷率，本示例設定紅方生存率/殺傷率的條件概率如表4所示。

表4 紅方生存率/殺傷率的條件概率表

4）殺傷率和生存率共同影響了指揮決策，本例設定指揮決策條件下生存率和殺傷率的概率如表5所示。

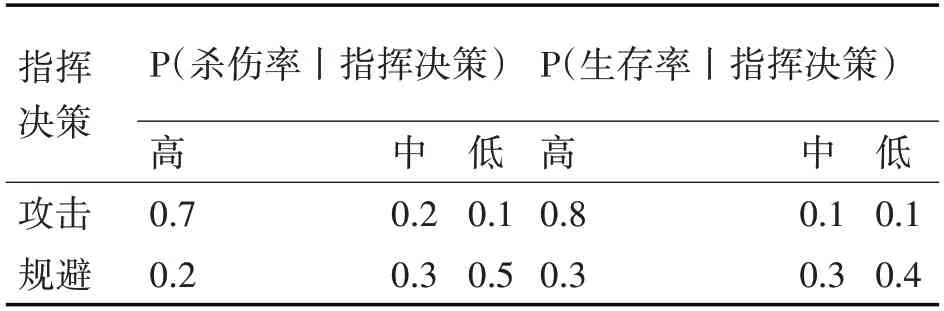
表5 指揮決策的條件概率表

5）相鄰時刻指揮決策的條件概率如表6 所示。

表6 貝葉斯網絡中相鄰時刻的條件概率表

以上參數為參考公開資料［8～11］后設定，只起到示例作用。在實際戰場中需要的參數十分嚴謹，可以通過綜合確定特征量，再通過大量樣本數據進行分析，在統計學的基礎上提高條件概率的準確性，從而提高推理計算的科學性。

4.3 模擬仿真

根據4.1 節描述的戰場背景，在構建貝葉斯網絡結構的基礎上，進行基于動態貝葉斯網絡的動態過程預測仿真實驗。在建模軟件的選擇上，選擇Netica 最終建立的模型如圖4。根據4.2 節設定的條件概率分布參數對網絡進行初始化，在相應的節點輸入對應的條件概率，如圖4 中的殺傷率（SSL）節點表示：在指揮決策（ZHJC）為攻擊（state0）時，殺傷率為高（state0）的概率為70%，為中（state1）的概率為20%，為低（state2）的概率為10%；在指揮決策（ZHJC）為規避（state1）時，殺傷率為高（state0）的概率為20%，為中（state1）的概率為30%，為低（state2）的概率為50%，使所有節點的條件概率與4.2節設定的參數一一對應。貝葉斯網絡模型的關聯線連接完畢后，點擊運行圖標以運行網絡，系統會根據數學概率公式自動計算節點概率，然后系統會進入待命狀態。在第一時刻獲取到新的戰場信息后，更新網絡模型中的觀測節點數據，網絡推理開始，得出的結果會是關于指揮決策各狀態的概率分布。表7為特征量在每一時刻的狀態值［12］。

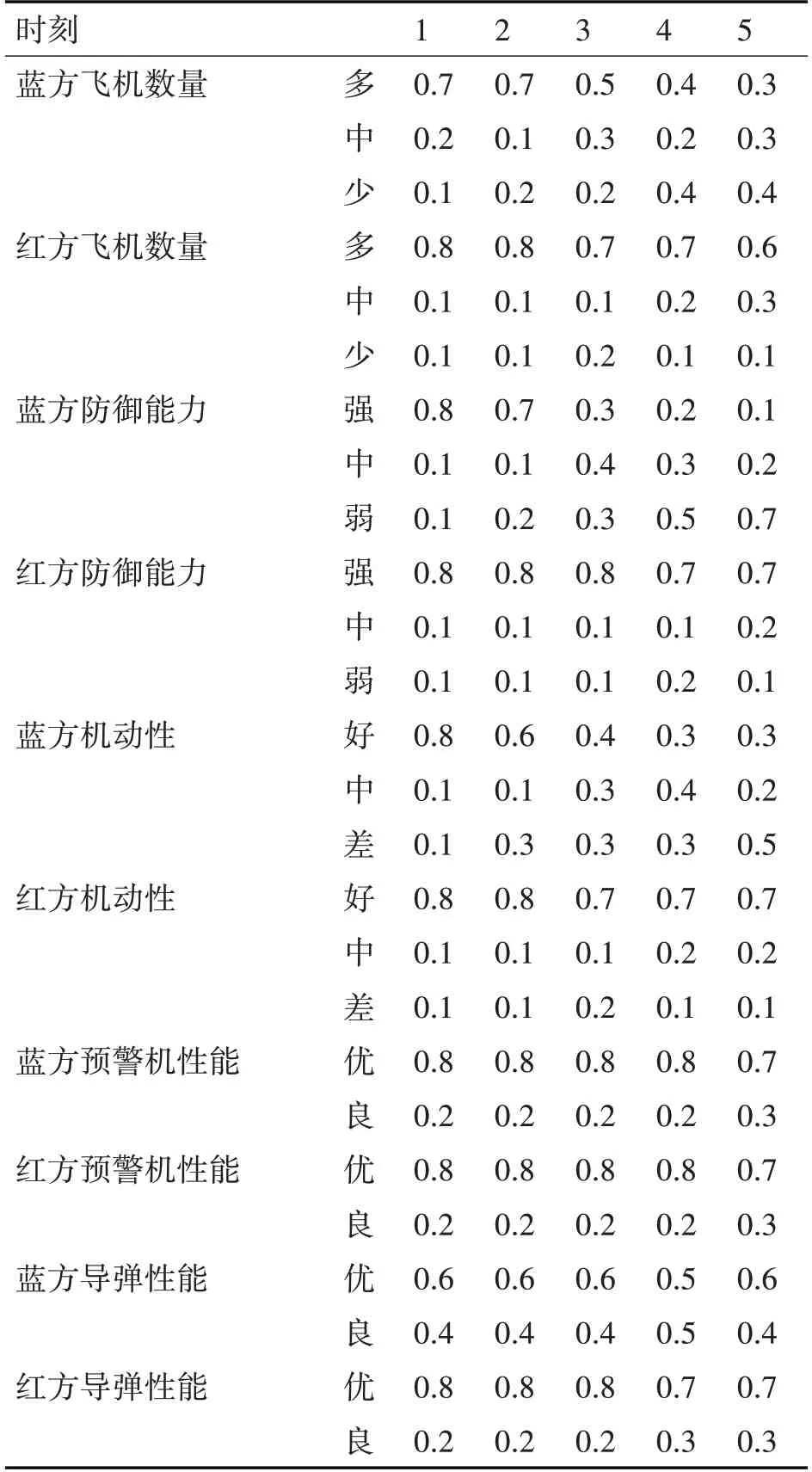
表7 特征量在每一時刻的變化值

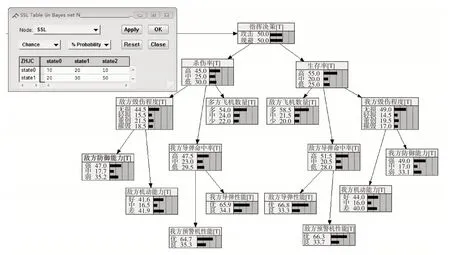
圖4 動態過程預測Netica仿真模型

從表7 數據來看，藍方飛機數量、防御能力、機動性都有不斷下降的趨勢，而紅方飛機數量、防御能力、機動性大體保持穩定；雙方預警機由于初始設定性能相近，又不參與直接作戰，故保持不變；導彈性能上紅方總體稍優于藍方。根據上面給出的觀測數據，利用Netica 模型計算可以得到各個時刻的殺傷率、生存率、指揮決策的概率分布如表8、表9、表10所示，第1時刻和第5時刻的模型如圖5、6所示。

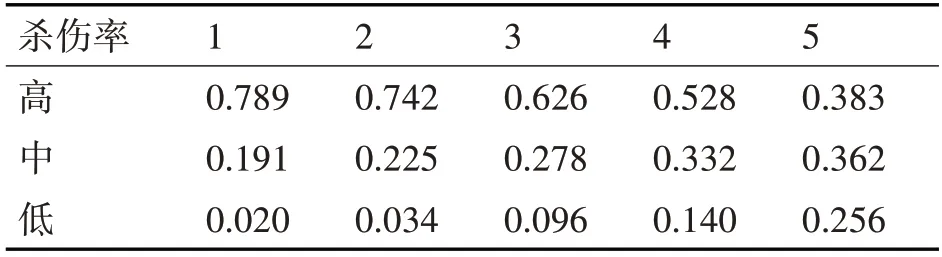
表8 殺傷率的動態貝葉斯推理結果

表9 生存率的動態貝葉斯推理結果

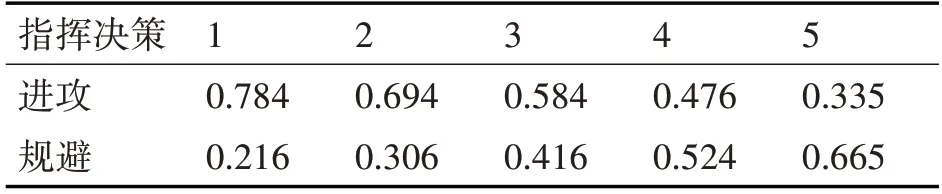
表10 指揮決策的動態貝葉斯推理結果

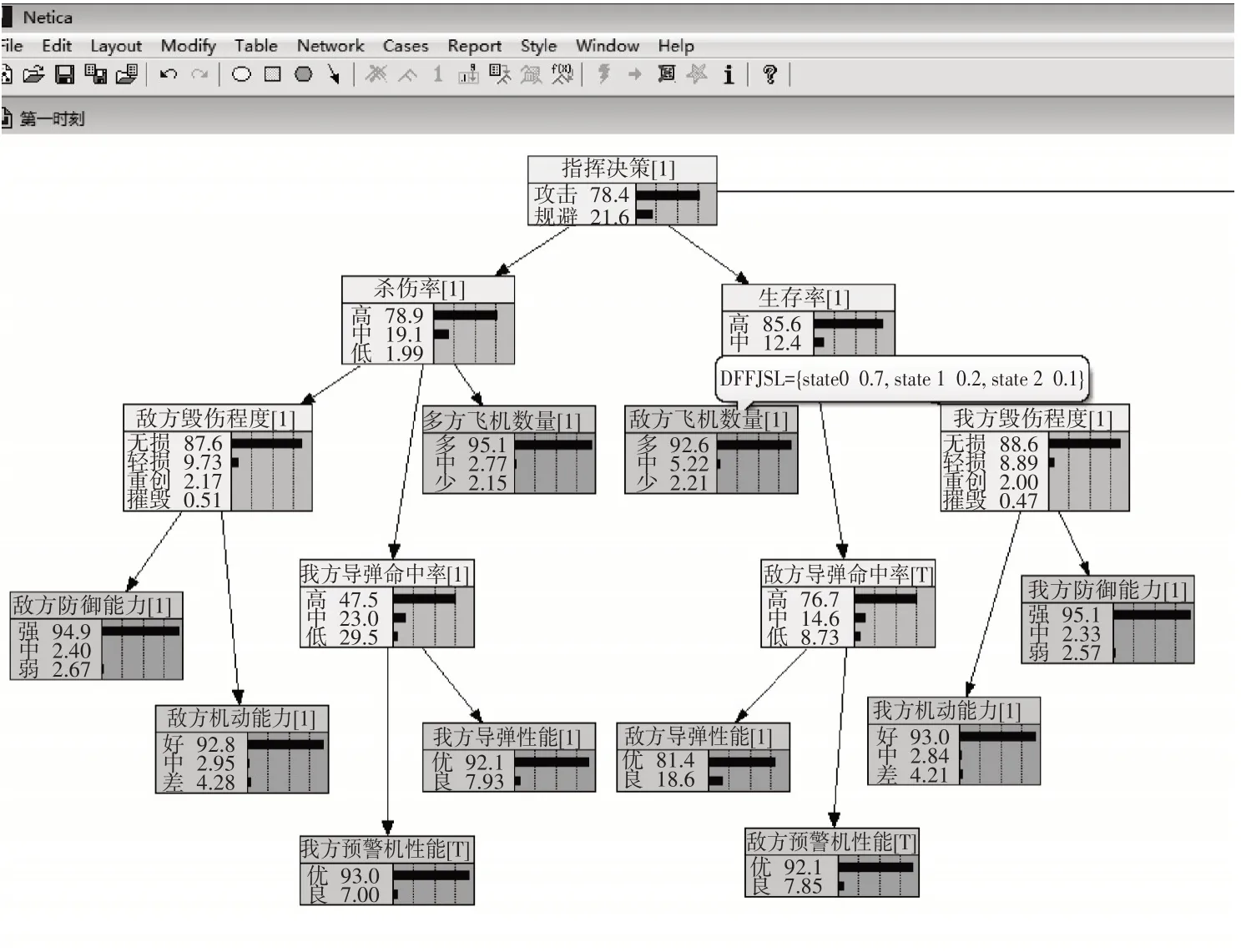
圖5 第1時刻各節點概率

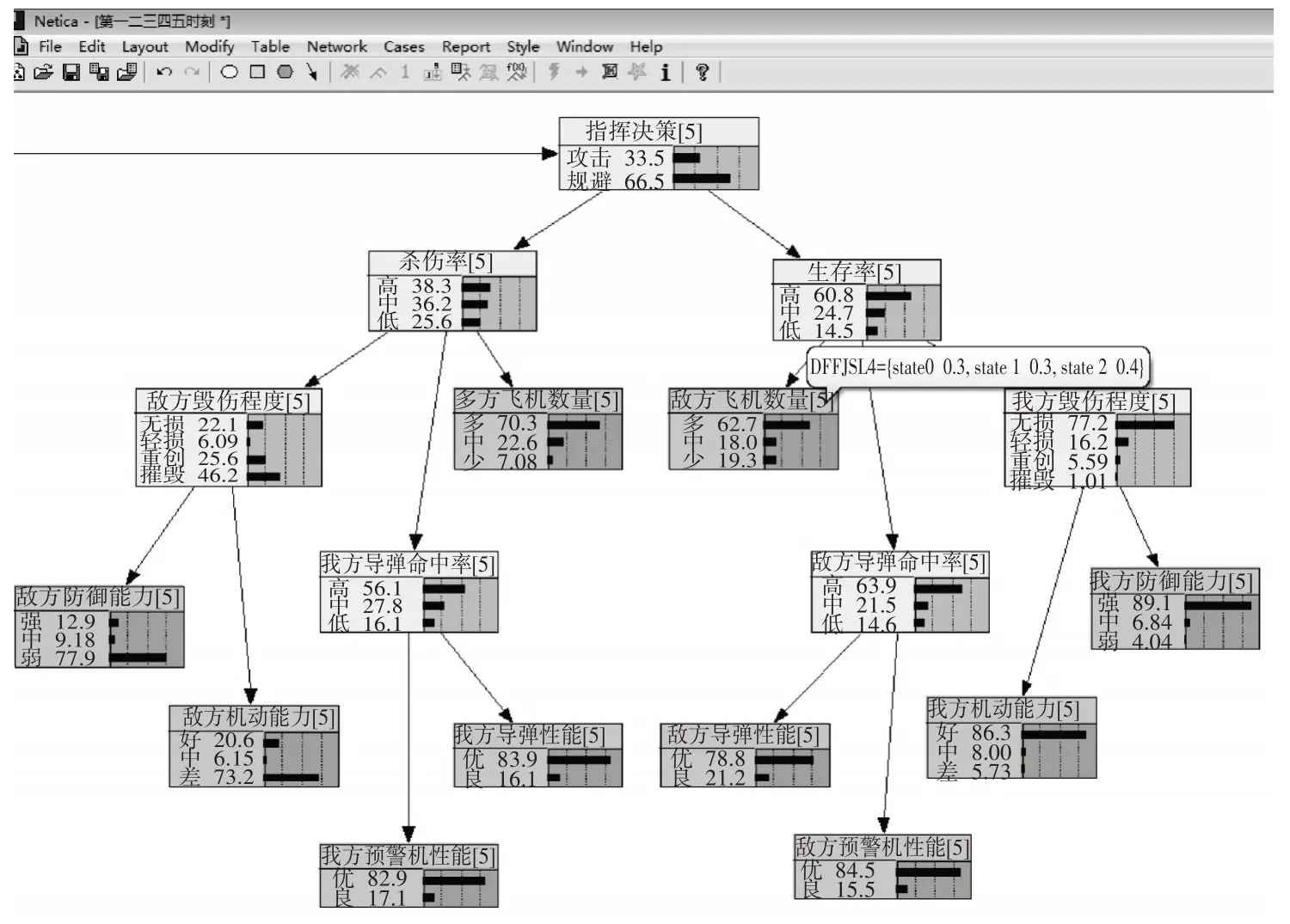
圖6 第5時刻各節點概率

4.4 仿真結果分析

表7 中的觀測數據反映出：隨著時間的推移，藍方的機動能力、防御能力逐漸減弱，飛機數量逐漸減少，表明藍方作戰力量在不斷削弱；而紅方的觀測節點數值變化不大，說明紅方作戰單元仍處在良好的狀態。

表8 和表9 給出了貝葉斯網絡仿真下5 個時刻的殺傷率和生存率的概率值，可以看出殺傷率和生存率為高的概率在逐漸減小，為低的概率在不斷增大，這是由于藍方的毀傷程度不斷增大，紅方在后一時刻摧毀的單位相較之前會有減少，并且紅方由于連續作戰，沒有其他支援兵力的補充，即便紅方的勝率很大，也會不斷有傷亡發生，但總體上紅方生存率較高。

由表10 可以看出進攻的概率是遞減的，但若將每個時刻“指揮決策”之間的連線斷開，使各自相互獨立，進攻的概率仍會很大。這是因為如果斷開以后相當于靜態的貝葉斯網絡，每一時刻之間并沒有任何聯系，進攻或是規避的判定完全由此刻雙方的狀態判定，紅方狀態好則進攻，藍方狀態好則規避。在創建的動態貝葉斯網絡中，前一刻的判定會影響后一刻，因為把“指揮決策”的條件概率設為當前一時刻為規避時，后一時刻規避的概率為1。這就使得整個網絡本身即使在不輸入任何觀測值的時候，每一時刻的進攻概率都在成倍降低，因此，在建立的這個動態貝葉斯網絡中，得出的進攻概率不斷降低的結論符合規律。之所以在己方狀態明顯好于藍方的情況下，進攻概率卻在不斷減小的原因是第1 時刻藍方的毀傷程度較低，雙方狀態相當，因此需要在下一時刻“繼續攻擊”的概率接近80%；從時刻3 開始，藍方的毀傷程度增高，紅方已經初步具備了一些優勢但并不明顯，因此需要二次進攻，但是“繼續攻擊”的概率比第1 時刻有所降低；到了第5 時刻，藍方單元已經接近被全部摧毀，此時需要“繼續攻擊”的概率為33.5%，說明繼續攻擊的價值很低，可以判定為如果繼續作戰，紅方勝率雖然很高，但因為藍方有生作戰力量很少，所以實際意義不大、性價比不高，可以選擇停止攻擊（規避）。在這個動態貝葉斯網絡中的“攻擊”實際上是“二次攻擊”。

從以上分析可以看出，在Netica 仿真下的動態過程預測結果符合實際且具有一定的可靠性，可以起到為指揮員提供決策參考的作用。另外在進行航母戰的動態過程預測時，可以使用這個網絡模型，通過增加有關艦艇的新的特征量使仿真結果更接近艦機協同作戰。在得到戰機對戰機的勝率后，可同理獲得艦艇對艦艇、艦艇對潛艇、飛機對艦艇等其他交戰結果，然后在專家意見下獲取各作戰類型相對于整個艦機協同作戰的條件分布概率，就可獲得該航母戰的獲勝概率。

5 結語

本文基于動態貝葉斯網絡對艦機協同作戰動態過程預測進行了仿真模擬。在分析艦機協同作戰的相關問題后，確定了七個特征變量，并根據特征變量之間的相互聯系確定了貝葉斯網絡結構，設定了一個案例背景進行仿真，在使用Netica 軟件建立基于貝葉斯網絡的仿真模型后，對網絡進行模擬，然后對結果進行了分析評估，評估結果符合戰場實際，可以達到對戰爭進行動態過程預測，為編隊指揮員提供正確決策的目的。