灌區新舊輸水渡槽協同防洪風險分析

劉開顏，付 湘，龔來紅，謝亨旺，劉雙郡

（1. 武漢大學 水資源工程與調度全國重點實驗室，湖北 武漢 430072；2. 武漢大學 海綿城市建設水系統科學湖北省重點實驗室，湖北 武漢 430072； 3. 江西省灌溉試驗中心站，江西 南昌 330201）

1 研究背景

在氣候變化與人類活動影響下，洪水風險加劇，嚴重威脅人民群眾的生命財產安全，影響了社會安定和經濟的可持續發展。正確評估水利工程防洪風險，是防洪減災領域的一項基礎性工作，以期為各項防洪減災措施制定與洪水風險管理提供重要依據。

近年來，國內外眾多學者對于水利工程防洪風險進行了大量的研究，主要集中在風險評估方法及模型應用方面：PHAM等［1］開發了一個基于混合人工智能模型的洪水風險框架，將AdaBoost 算法與決策表結合，利用洪水敏感性圖和洪水后果圖生成洪水風險圖，在缺乏時間序列氣象和流量數據的情況下也可以對洪水風險進行評估；王文圣等［2］明確了次風險和年風險兩種洪水風險概念，探討以年最大洪水信息為基礎的年風險度和以年內最大及次大洪水信息為基礎的年風險度的差異；周方明等［3］針對水庫大壩的水文、水力及工程結構等因素的不確定性，構建了時變隨機變量量化的函數模型和緩變型防洪風險分析模型，定量分析大壩防洪安全；楊震宇等［4］針對三峽水庫汛期中小洪水調度中的各類風險問題，分析中小洪水的特性，并建立各類風險指示函數，提出了防洪、地質、發電等多角度的中小洪水調度性能風險評估方法。FLORES 等［5］提出了一種面向對象的混合動態貝葉斯網絡，得到的模型能夠較為準確地預測洪水水位，由此對地中海流域洪水風險進行了評估；HOSSEINI等［6］使用GLMBoost、RF 和BayesGLM 三種最先進的機器學習模型對受洪水強烈影響的地區的山洪暴發進行建模，能夠有效地預測數據稀缺地區的洪水風險；陳華等［7］利用防洪安全領域積累的監測數據，通過融合態勢感知相關理論，提出面向流域防洪安全的態勢圖譜構建及可視化方法，并應用于丹江口庫區；張丹等［8］建立了風險評估的模糊灰關聯故障樹模型以識別及評估水利水電工程的社會穩定風險；NACHAPPA 等［9］耦合多準則決策分析模型及機器學習模型繪制基于11 個洪水調節因素得出的洪水敏感性圖，并使用Dempster Shafer理論優化，該方法在全球都具有普適性，為洪水評估和預防提供了較為準確的結果；張啟義等［10］總結五類主要防洪風險事件，再利用故障樹法識別各類風險事件的風險因子，在對現狀條件下所有左排渡槽的防洪風險因子進行詳細調查的基礎上，有針對性地提出了除險及防范措施；張曉琦等［11］將經濟學條件風險價值理論引入防洪評價領域，辨識各水庫防洪庫容值對庫群系統防洪風險的影響程度及各水庫間協同防洪的互饋方式。

輸水渡槽作為水利工程中的重要組成部分，承擔著防洪、供水、航運等多項功能，對于工程沿線的人民生活有著重大的影響，故對其防洪風險進行合理的評價研究，對于水利工程整體的防洪安全意義重大［12，13］。馮平等［14］采用二維復合事件風險組合模型，通過兩兩組合求解南水北調中線工程總干渠河北省段的防洪風險，但該模型只考慮了水文要素，并沒有考慮工程本身的結構等特征。賈超等［15］對渡槽結構逐一進行了破壞模式的分析，建立了相應的功能函數，計算出渡槽側板、底板、底梁等結構的可靠指標，但他只考慮了渡槽中水體對渡槽的作用，沒有從水文因素的角度考慮長距離輸水工程的風險。陳進［16］等采用系統和風險分析理論，從水文、建筑物、經濟、政策、環境和社會等方面分析了跨流域長距離調水工程系統的風險因子及影響方式，對調水工程建設和運行過程中的各類風險進行了初步的風險評價。

水利工程正常運行多年后，由于自然或人為因素的影響導致運行條件較原設計發生變化，引發防洪安全問題，評估運行條件變化后的工程所面臨的防洪風險對其安全運行管理具有重大意義。因此本文以江西省贛撫平原崗前渡槽為研究對象，綜合考慮水文、工程結構等特性，依據其工程設計與運行現狀整理分析新、舊崗前渡槽的特征控制水位。針對洪峰流量符合皮爾遜三型（P-Ⅲ）分布和正態分布的兩種情況，依據調洪計算方法進行典型洪水過程的“峰比”放大得到洪水輸入數據，以特征控制水位為約束條件，運用蒙特卡羅隨機模擬方法求解新舊崗前渡槽協同防洪風險。

2 研究方法

為了定量描述渡槽承擔的防洪風險，可將其定義為：在規定的時間內，天然來（洪）水超過渡槽的輸水能力的概率［17，18］，若渡槽有最低安全運行水位的要求，則定義可進一步轉化為：在規定時間內，渡槽內流量超過其設計流量或低于其防洪安全運行最小流量的概率，數學表達式為：

式中：RP表示發生頻率為P的洪水時渡槽承擔的防洪風險；Qkt表示第k個渡槽在第t時段內的流量，m3/s；Qkd表示第k個渡槽的設計洪水流量，m3/s；Qks表示第k個渡槽能維持防洪安全運行的最小流量，m3/s。

為了利用公式（1）進行風險計算，考慮Qkt的隨機分布：假設天然來（洪）水最大洪峰流量概率密度分布函數f(Qm)是P-Ⅲ分布或正態分布，則任一頻率P對應的洪峰流量Qm可由函數求得，再采用同倍比放大法放大典型洪水過程線，使放大后的洪峰流量等于設計洪峰流量Qm，令其出現的頻率等于設計標準P，即認為所得的過程線是待求的設計洪水過程線。

若時段內天然來（洪）水最大洪峰流量概率密度分布函數f(Qm)滿足P-Ⅲ分布，則表達式為［19］：

式中：α、β、a0為P-Ⅲ型分布的形狀、尺度和位置參數；Γ(α)為α的伽馬函數。

3個參數α、β、a0的計算方法如下：

式中：EX為總體均值；Cs為偏態系數；Cv為變差系數。

若時段內天然來（洪）水最大洪峰流量概率密度分布函數f(Qm)滿足正態分布，則表達式為：

式中：σ為標準差； e為自然對數的底。

渡槽內水位和流量的對應關系可以通過明渠均勻流公式建立，當渡槽的坡度較為平緩且過水斷面為矩形時，各時段流量與水位的計算公式如下：

式中：Akt表示第k個渡槽在第t時段的過水斷面面積，m2；Ckt表示第k個渡槽在第t時段的謝才系數；Rkt表示第k個渡槽在第t時段的水力半徑m；ik表示第k個渡槽的坡度；dk表示第k個渡槽過水斷面的寬度，m；hkt表示第k個渡槽在第t時段內水平面距離槽底的高度，m。

由于公式（2）和（4）難以具體求解，故本文應用蒙特卡羅方法 （Monte-Carlo法，簡稱MC法）求解。

MC 法屬于試驗數學，它利用隨機數進行統計試驗，以求得均值與概率等統計特征值作為代解問題的數值解。該方法的主要思路是：按照概率定義，某事件的概率可能用大量試驗中該事件發生的概率估算。因此，先對基本隨機變量的分布函數FXi(xi)進行N次隨機抽樣，獲得各變量的隨機數x（jij=1，…，N），然后把這些抽樣函數值代人功能函數式，得N個Zj值（j=1，…，N），統計Zj＜0 的失效次數Nf，并算出失效次數與總抽樣次數的比值，此值即為所求的風險值的無偏估計量。

當樣本容量N足夠大時，MC 法的精度可由大數定理和中心極限定理求得［20］：

式中：ε為與Rf的相對誤差。

由公式（7）可知蒙特卡羅方法的樣本容量N與置信度1 -α、相對誤差ε和風險值的無偏估計量均有關。在置信度確定的情況下，為使得風險值趨于穩定且相對誤差較小，應取盡可能大的N。一般而言，采用蒙特卡羅法求解問題，往往需要數千乃至數萬次的模擬計算。

3 工程實例應用

3.1 研究區域概況

崗前渡槽位于江西省贛撫平原灌區，跨越清豐山溪排洪道，具體地理位置見圖1。崗前渡槽是江西省最大的渡槽，作為崗前水利樞紐的重要組成部分，主要承擔灌溉、供水和航運等功能，渡槽于1958年冬動工興建，1959年7月開始通水使用，在此期間渡槽促進了當地工農業生產，并且抵御了1982年特大洪水，在地區經濟社會發展中發揮著舉足輕重的作用。

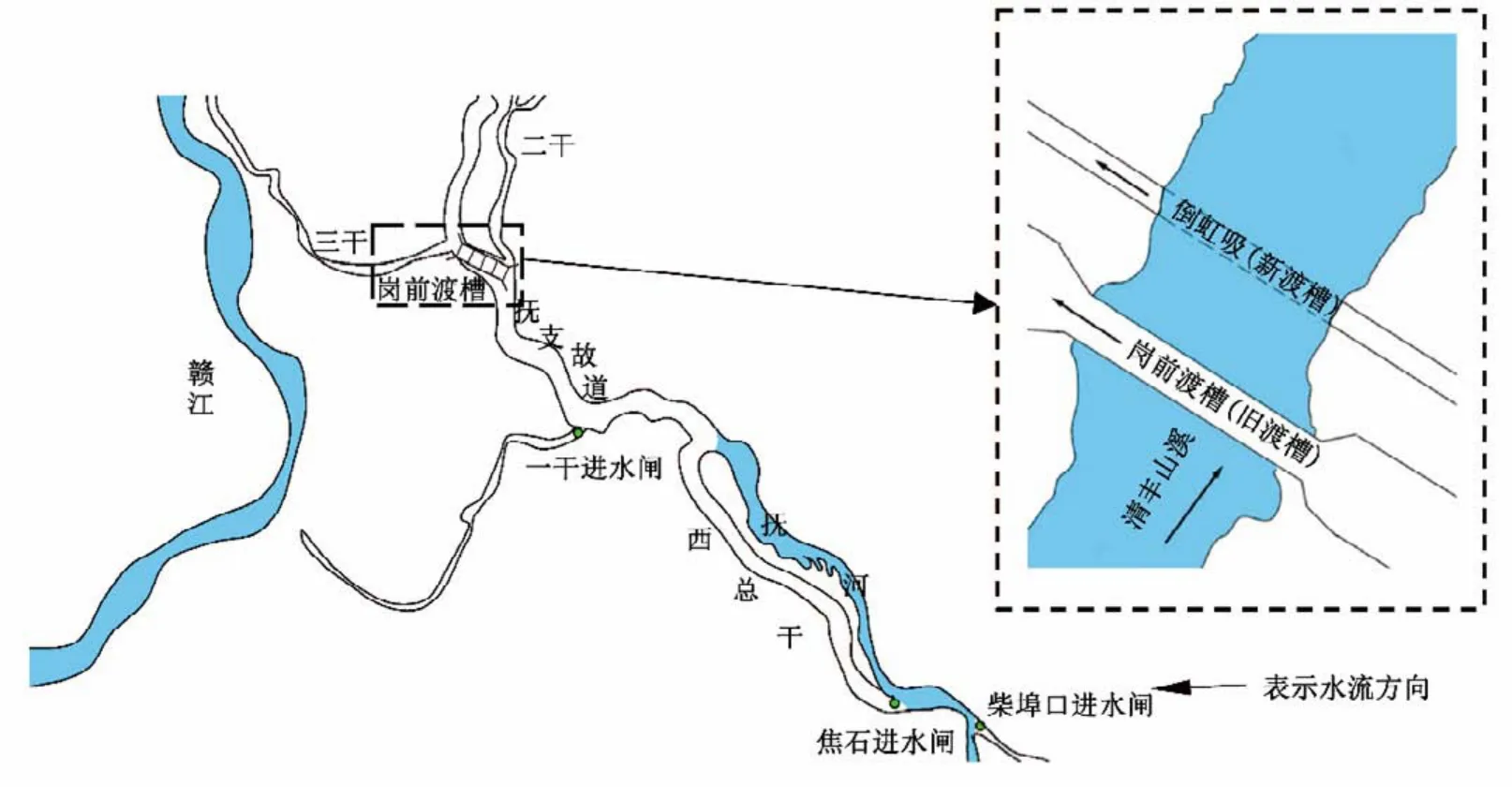
圖1 贛撫平原灌區水系分布及崗前渡槽位置示意圖Fig.1 Schematic diagram of drainage system distribution and position of Gangqian Aqueduct in Ganfu Plain Irrigation Area

但崗前渡槽運行60 余年，逐漸出現混凝土老化剝蝕、槽身開裂漏水、槽下淤泥堆積導致凈空不足等安全問題，在2020 年4月《江西省贛撫平原灌區崗前渡槽安全鑒定報告》中被定性為四類渡槽，無法滿足設計條件下的安全運行。2020 年9 月江西省水利廳、江西省發展和改革委員會決定采取在崗前渡槽下游側（清豐山溪）66 m 處修建一個埋式倒虹吸作為新渡槽，以替代崗前渡槽在灌區中的供水及灌溉功能，現狀崗前渡槽（簡稱舊渡槽）只承擔航運功能。

3.2 輸入資料及參數分析

新舊渡槽的工程設計參數和現狀運行參數見表1。表1 中具體數據均來自《江西省贛撫平原灌區“十四五”續建配套與現代化改造（二期）可行性研究報告》。其中，新渡槽采取3 根4.2 m×4.2 m 的矩形管道，且最大過水流量為113 m3/s，報告中均稱其為新渡槽的加大流量，因此本文新渡槽的加大流量取值為113 m3/s，見表1。

表1 新舊渡槽的有關參數Tab.1 Related parameters of the old and new aqueducts

依據報告確定渡槽的特征水位和特征流量后，考慮到崗前渡槽過水斷面為矩形且坡度i=0.000 1，運用公式（5）建立舊渡槽特征水位與特征流量的對應關系，具體數據見表2。

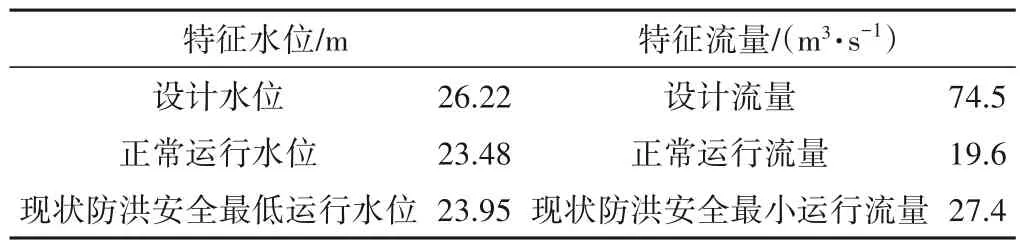
表2 舊渡槽特征水位和特征流量的對應關系Tab.2 Correspondence between characteristic water level and characteristic discharge of the old aqueduct

報告指出“現狀崗前渡槽運行水深不超過2.0 m 時（大于Ⅵ級航道最低運行水深1.0～1.2 m），渡槽結構滿足安全運行要求”，故令舊渡槽正常運行的最高水位是23.48 m。同時報告中寫明“現狀崗前渡槽在遭遇清豐山溪20 年一遇設計洪水時，槽內水位低于23.95 m 時槽身的抗滑、抗傾穩定均不滿足規范要求”，因此，公式（1）中的渡槽能維持防洪安全運行的最小流量為舊渡槽水位23.95 m對應的流量值，即取值為27.4 m3/s。新渡槽作為續建工程，需要承擔除航運外的各項功能并保障舊渡槽的工程安全，公式（1）中的渡槽設計洪水流量為設計流量74.5 m3/s，具體數據見表2。

利用公式（2）～（4）計算洪峰流量Qm的P-Ⅲ型分布和正態分布。渡槽本身流量數據不足，但臨近的吳石水文站擁有較為完整的60 年流量數據，考慮到贛撫平原屬于小流域，所以可以綜合渡槽已知數據和吳石站的水文數據確定設計洪水的參數，用樣本統計參數近似替代總體的統計參數可得：均值EX=68.23 m3/s、偏態系數Cs=1.89、變差系數Cv=0.63。將上述參數代入公式（2）～（4），得到兩種分布的密度函數圖像如圖2所示。

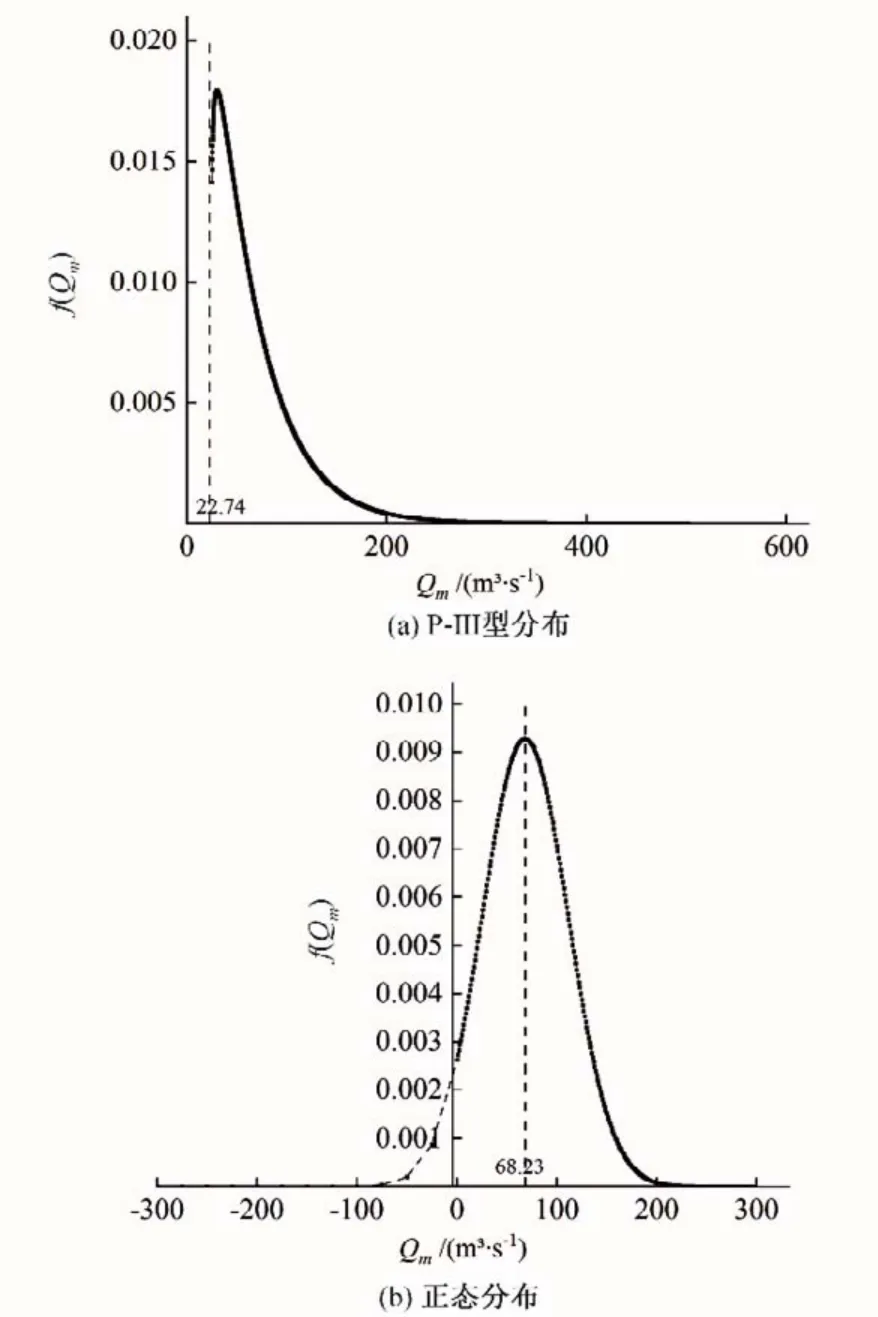
圖2 洪峰流量Qm的P-Ⅲ型分布和正態分布圖像Fig.2 P-Ⅲ distribution and normal distribution of Qm

圖2（a）為洪峰流量Qm符合P-Ⅲ型分布的概率密度函數圖像，圖中虛線為Qm= 22.74 =a0，為圖像的漸近線。圖2（b）為洪峰流量Qm符合P-Ⅲ型分布的概率密度函數圖像，圖中虛直線表示Qm= 68.23 =EX，為圖像的對稱軸；圖中的虛曲線表示Qm＜0，不符合實際情況，故用虛線表示。

從崗前渡槽2011-2018 年的歷史流量數據中，選取最大15日流量作為典型洪水過程，以1 h 為一個時段繪制典型洪水過程線，具體見圖3。

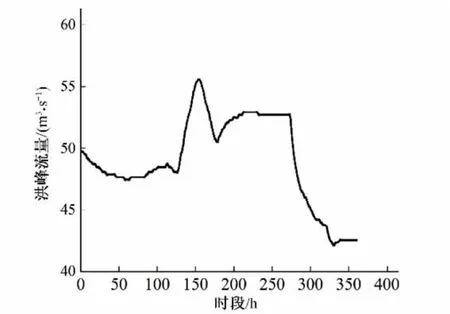
圖3 典型洪水過程圖Fig.3 Typical flood process diagram

3.3 渡槽防洪風險計算

考慮到渡槽本身結構的脆弱性和極端降雨事件的突發性，本文采取超過現狀設計洪水的洪水流量來計算新舊渡槽協同防洪風險。

根據MC法原理，利用Matlab R2020b編程得到符合P-Ⅲ分布的偽隨機數Qm，p-Ⅲ和符合正態分布的偽隨機數Qm-φ，要求生成的偽隨機數均大于舊渡槽現狀防洪安全最小運行流量與新渡槽設計流量之和101.9 m3/s，即模擬高于現狀設計流量的較為不利的洪水情景，以偽隨機數作為設計洪峰，運用“峰比”放大法放大典型洪水，計算對應的設計洪水過程線。

采用公式（1），分別計算8 種情景下渡槽承擔的防洪風險，結合公式（6）～（7）以及程序運行的效率和數據的收斂效果確定隨機模擬次數，最終得到新舊渡槽防洪風險具體見圖4和表3。

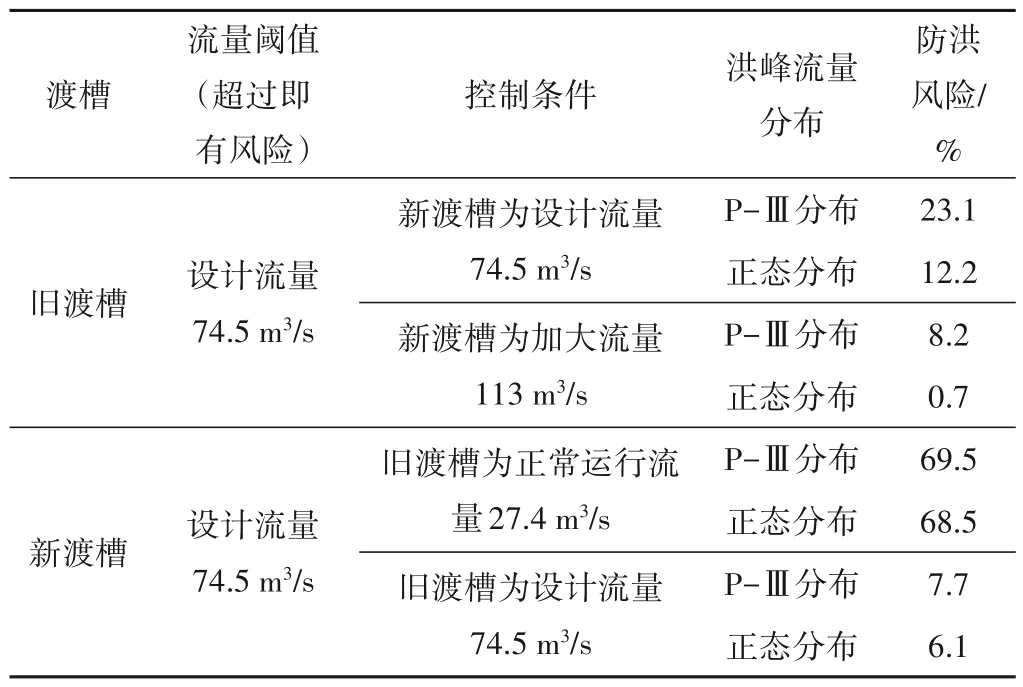
表3 MC法模擬新舊渡槽防洪風險的收斂結果Tab.3 Convergence results of MC method to simulate flood risks of the old and new aqueducts

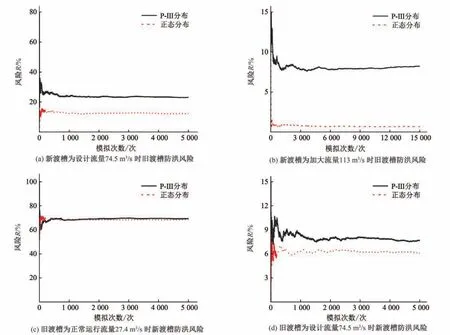
圖4 模擬次數與渡槽防洪風險關系圖Fig.4 Relationship between simulation times and aqueduct flood risk

圖4（a）表示新渡槽流量為其設計流量74.5 m3/s 時，若洪峰流量分布分別滿足P-Ⅲ分布和正態分布，經過5 000 次隨機模擬后，舊渡槽所承擔的防洪風險分別穩定在23.1%和12.2%；圖4（b）表示當新渡槽流量為其加大流量113 m3/s 時，若洪峰流量分布分別滿足P-Ⅲ分布和正態分布，經過15 000 次隨機模擬后，舊渡槽所承擔的防洪風險分別穩定在8.2%和0.7%。圖4（a）、（b）比較表明，當超過現狀設計流量的洪水來臨時，讓新渡槽按加大流量運行可以大幅降低舊渡槽的防洪風險。

圖4（c）表示舊渡槽流量為其正常運行流量27.4 m3/s 時，若洪峰流量分布分別滿足P-Ⅲ分布和正態分布，經過5 000 次隨機模擬后，新渡槽所承擔的防洪風險分別穩定在69.5%和68.5%；圖4（d）表示當舊渡槽流量為其設計流量74.5 m3/s時，若洪峰流量分布分別滿足P-Ⅲ分布和正態分布，經過5 000 次隨機模擬后，新渡槽所承擔的防洪風險分別穩定在7.7%和6.1%。圖4（c）、（d）比較表明，超過現狀設計流量的洪水來臨時，讓舊渡槽按照設計流量泄洪可以有效降低新渡槽超設計流量運行的風險。

表3 展示了8 種情景下渡槽的防洪風險，由表3 中數據可知：當新渡槽按加大流量運行時，兩種不同的洪峰分布下，舊渡槽的防洪風險分別降低了64.5%和94.3%；當舊渡槽按設計流量運行時，兩種不同的洪峰分布下，新渡槽的防洪風險分別降低了88.9%和91.1%，體現出新舊渡槽協同防洪的重要性和有效性。

在其余條件相同的情況下，P-Ⅲ分布的計算結果比正態分布平均偏高40.2%，說明洪峰分布采取P-Ⅲ分布可以模擬更加不利的洪水條件，在工程設計施工和后期運行時運用該分布確定設計和運行的參數，可以提升工程的安全性。

4 結 論

本文提出了新舊輸水渡槽協同防洪風險分析方法，以江西省贛撫平原灌區的新舊輸水渡槽為例，得出以下結論。

（1）選取超過20 年一遇標準的設計洪水作為流量輸入，若新渡槽為設計流量74.5 m3/s，經過5 000 次隨機模擬，舊渡槽防洪風險值趨于穩定，若新渡槽為加大流量113 m3/s，需經過15 000 次隨機模擬，舊渡槽防洪風險才達到穩定值，說明蒙特卡羅方法受變量和風險大小的制約，需要增加模擬次數以提高精度。

（2）渡槽洪峰流量分布擬合采用了P-Ⅲ分布和正態分布兩種函數，在其余條件相同的情況下，P-Ⅲ分布計算結果得到的渡槽防洪風險均比正態分布高，說明在工程設計施工和后期運行的情況下，洪峰分布采取P-Ⅲ分布可以模擬更加不利的洪水條件，提升工程的安全性。

（3）渡槽遭遇的洪水超過20 年一遇防洪標準時，舊渡槽若按正常運行流量27.4 m3/s 泄洪，則新渡槽承擔防洪風險過大（約為70%）；若新舊渡槽均按設計流量74.5 m3/s 泄洪，則舊渡槽仍存在較大的防洪風險（約為18%），故應適時令新渡槽按加大流量泄洪，使舊渡槽防洪風險大幅降低，達到新舊渡槽協同防洪的效果。

灌區現有的水利設施經過長期運行，存在不同程度的安全問題，難以滿足設計條件下的安全運行，續建新工程代替其部分功能是解決方法之一。研究新舊渡槽協同防洪對于其他現有水利工程和新建工程協同防洪有重要的參考價值。面臨超設計標準的洪水時，分配新舊工程承擔洪水量的大小會導致不一樣的工程防洪風險，對此進行評估有利于后續制定新舊工程協同調度規則，維護工程正常運行管理。