豎向荷載作用下連梁樁結構基礎梁承載力試驗分析

梁 宸 （安徽省建筑科學研究設計院，安徽 合肥 230031）

1 引言

連梁結構在樁基中被廣泛使用。抗滑樁頂部的連梁可以將不同位置的樁連接成一個整體結構，使樁受到均勻的力和變形，增強樁土的相互作用。樁頂與聯結梁相連的結構在道路地基中也有發現，可以有效抑制路堤的側向變形，提高路堤的穩定性[1]。在此基礎上，本文將連梁結構引入到高層建筑的地基中，提出一種改進的樁群地基，稱為連梁樁結構地基。通過將梁與樁群基礎的樁身頂部剛性連接，可以作為傳力結構將荷載均勻地傳遞到各下層樁身，并自身承擔部分荷載。極大增加了樁群基礎的承載力，改善了差異沉降現象[2]。與異型截面樁相比，連梁結構的下部仍然是普通的圓樁，而梁結構的上部是地梁或地下連續墻，其施工方法已經非常成熟，簡單、造價低[3]。目前對連梁樁結構的研究大多是對穩定性和水平承載力的考慮，而對各種梁體參數和豎向承載力的優化關注很少。在本研究中，采用3m×3m 的樁群構建了一個連梁樁的設計，并利用有限元軟件對梁的寬度、長度和剛度進行了調整，得到了梁的最佳結構參數，為地基處理提供新的建議。

2 實驗方案

在巖土工程中，能否真實地反映樁土相互作用對數值模擬軟件提出了很高的要求，ABAQUS 基于Mohr-Coulomb屈服準則的理想彈塑性模型是模擬土的非線性特征最廣泛的應用。因此本文建立了一個3m×3m 樁群連梁樁結構的尺規模型進行分析。樁體定義為彈性，樁體和連梁樁結構高度共10m，樁徑取0．2m，樁間距為1．8m，連梁寬度為0．5m，樁體與高度為0．5m 的承臺相連，土體選擇Mohr-Coulomb 主模型，保證從樁體到邊界有足夠的空間來抵消邊界效應。土體的長度為24m，寬度為24m，高度為20m。樁與土壤的方向接觸采用“硬”接觸[4]，限制樁進入土壤，切向接觸采用“罰”函數來定義摩擦，摩擦系數是土壤內摩擦角的正切值。為了限制模型在計算過程中在剛體中移動，土壤周圍和底部的位移在法線方向被設置為零。首先施加一個地應力平衡，然后在承載平臺表面施加一個垂直載荷。網格單元由C3D8R 劃分，并對樁土接觸區的網格進行了適當的細化。

為了計算連梁和樁之間的軸向力，將數值模型的測量點設置為每個樁有六個應變片，頂部連梁有兩個應變片。將自然密度為1．94g/cm3的黃土分層壓實，并在模型中進行平整，以達到作為地基填料的一致性。裝載設備使用一個10t的液壓千斤頂，總共有八級裝載。每一級荷載轉換后為28．36kPa，當每一級荷載穩定后再進行下一級荷載，如圖1所示。

圖1 網格劃分

3 連梁的優化分析

連梁樁結構的樁距、樁長和長徑比都會對樁的承載能力和受力方式產生顯著影響。而在連梁樁結構中，連梁的寬度、長度和剛度起著重要作用。在前述模型的基礎上，連梁的寬度（D）、長度（S）和剛度是變化的。然后對其施加9000kN的豎向荷載，分析各種因素對連梁樁結構的承載特性和荷載傳遞狀況的影響，并作為連梁樁結構最佳設計的指導。

3.1 連梁寬度

較大的荷載可以通過連梁與垂直荷載下的樁體連接處的可變截面來承載并傳遞到土壤中。不同的連梁寬度會改變橫截面積，對連梁樁結構的承載能力有很大影響。連梁寬度（D）分別為0．4m、0．5m、0．6m、0．7m 和0．8m，其余參數保持不變，建立模型并提取沉降量，如圖1所示。連梁寬度和結構的沉降存在負相關；沉降隨著連梁寬度的減少而增加。兩者之間有明顯的差異，在9000kN 荷載下的最大沉降為233．59mm，最小沉降為162．86mm，相差30．28%。當連梁寬度為0．4 和0．5m 時，沉降量比較接近，對承載力的提高不明顯，在9000kN僅相差3．11%，而D 在0．5m 至0．8m 時可減少沉降8．25%、11．17%和11．65%，連梁寬度對結構的沉降影響比較明顯。

選取中樁的軸向力進而來分析結構的受力情況，如圖2 所示。在不同的載荷下，軸向力的分布基本相同，隨著連梁寬度的減小而增加。連梁樁越寬，連接處的接觸面積就越大，轉移到土壤中的荷載就越多，連梁樁和下層樁所承受的荷載就越少。且本文中的樁頂連梁樁的結構與普通樁體結構相似，因此越寬的梁不一定更好。連梁越寬，連梁與支座形成的封閉隔間越小，隔間內被墻體側壁和上部支座包裹的土心的壓縮作用越明顯，其所能提供的摩擦阻力越小。同時，墻角越近，應力集中的效果越明顯，從而使內部土芯受到“墻群效應”的干擾越大。土的承載力被削弱，需要地基承受更多的負荷[5]，導致連梁處的軸向力增加。除了對連梁有影響外，這種影響還將提高樁的負荷。在9000kN 下，連梁寬度為0．8m 的下層樁存在最大的軸向力，因此連梁樁將承受更大的載荷。

圖2 荷載沉降曲線

3.2 連梁長度

連梁長度的變化會影響梁與土的接觸面積，并改變樁距，這對地基的承載力有較大影響。連梁長度（S）設定為1．4m、1．6m、1．8m、2．0m、2．2m，其余參數與初始模型保持一致。對不同梁長的荷載-沉降曲線的分析顯示表明（圖3），沉降的幅度隨著梁長的增加而減少。從1．4m 到1．6m，沉降減少了22．65%；從1．6m 到1．8m，沉降減少21．15%；從1．8m 到2．0m，減少16．74%，從2．0m 到2．2m，減少15．13%，沉降均有較大的變化。且連梁長度的增加可以增加樁距，從而減少“樁群效應”，進而增加地基的承載力。連梁的能力隨著長度的增加而增加，與樁的接觸面積和可以轉移到土壤中，載荷也會增加。

圖3 不同連梁寬條件下的中間樁軸向力

選擇中間的樁繪制軸向力分布曲線，如圖4 所示。連梁的長度越大，相應的連梁軸向力就越大。“樁群效應”使連梁長度為1．4m 時的樁身受到的干擾較大，軸向力較小，當連梁長度為1．4m 和1．6m 的連梁軸向力差異較大。在連梁長度為4m 的較低荷載下，下層樁身的軸向力最小，在較高荷載下，樁身周圍的土體受到破壞，更多地依靠下層樁身來承受荷載，軸向力最大。當連梁長度為2．2m 時，在較低的荷載下軸力最大，但在較高的荷載下，樁身的軸力最小，連梁的軸力也比連梁長度為2．0m 時小，與1．8m 時的軸力比較接近，這與前面的分析相反。當連梁長度為2．2m 時，“樁群效應”降低，極限承載力明顯大于其余的樁群。由于在2．2m 處的效果還沒有達到，當該組的其余結構部分接近損壞時，其中心樁的軸向力較小。

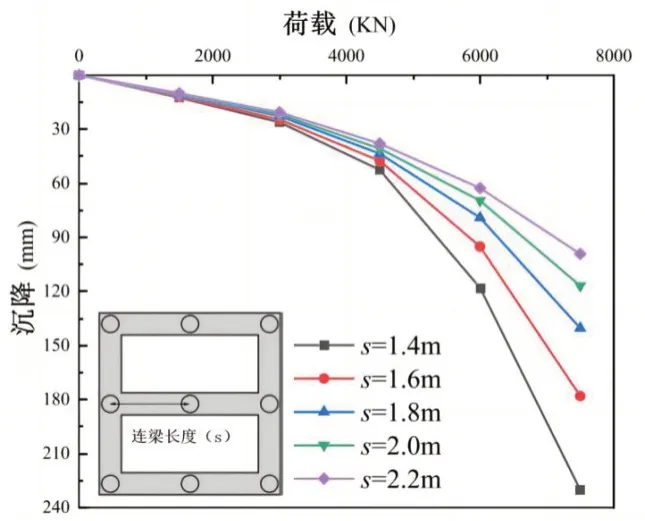
圖4 荷載沉降曲線

為進一步分析不同連梁長度的影響，考慮了9000kN 的載荷，研究連梁的軸向力和土壓力，如圖5和圖6所示。連梁的軸向力隨著樁距的增加而穩步增加。當荷載為9000kN 時，連梁長度值為1．8m、2．0m、2m 的連梁的軸向力沒有明顯差異，數值分布為2．0m＞1．8m＞2．2m。當荷載較低時，連梁長度值為2m 的連梁的拉力最大，隨著荷載的增加，上升速度穩步下降。當載荷從7500kN 增加到9000kN 時，連梁長度值為1．4m 和1．6m 的連接梁的軸向力基本保持不變。此時，這兩個長度的連梁基本上已經失去了承載能力。對于不同連梁長度值下的土壓力，與前面的分析一致，1．4m 和1．6m 的土壓力在6000kN后出現了明顯的變化（圖6），1．8m 在9000kN的荷載下表現出了下降的現象，這基本上是連梁長度為1．8m 時的極限承載力，而2．0m 和2．2m 的土壓力則保持線性。基于以上分析，連梁樁結構的連梁長度不能選得太小，即連梁長度至少要在1．8m 以上或4．5 倍樁徑，因為連梁長度太小會造成“樁群效應”，導致承載力降低。當連梁長度為2．2m 或5．5倍樁徑時，受“樁群效應”影響較小。根據樁基的技術規范，當樁群的連梁長度超過樁徑的6 倍時，可以不考慮“樁群效應”。上述研究表明，當連梁長度大于6倍樁徑時，連梁樁結構基本上可以不考慮“樁群效應”，因為很難準確核算單樁承載力或計算出樁群效率系數。

圖5 不同連梁長度下的中間樁軸向力

圖6 連梁在不同連梁長度下的軸向力

3.3 連接梁與樁的剛度比

連梁樁結構中的連梁既能承受荷載又能傳遞荷載，連梁的剛度對結構的整體荷載再分配有重要影響。以樁的彈性模量20GPa 為基準，連梁的彈性模量分別為基準值的0．5、1、1．5、5、10 倍。其余的參數與初始模型相同，連梁沉降量如圖7 所示。五種不同剛度下的荷載沉降曲線幾乎相同，相差僅1～2mm，說明梁的剛度對垂直荷載下結構沉降的影響幾乎為零。梁的剛度對連梁樁結構支撐垂直荷載的能力沒有影響。

圖7 不同連梁長度土壓力

通過改變連梁的剛度來改變結構受力，提取不同剛度比的連梁樁的軸向力，如圖8 所示。在較高和較低的載荷下，軸向力的大小和分布基本相同。連梁剛度的增加對樁的軸向力有一定影響，但影響不大，主要是影響連梁軸力。在參考值的1．5 倍時，梁的軸向力最大，5 倍時最小，但幅度相近，因此梁的剛度對結構的沉降影響較小。在樁和連梁的連接處，連梁的剛度越大，連接的曲線就越平滑，傳遞到下層樁的力就越大。連梁的剛度越大，并不意味著連梁將承擔更多的載荷，而是意味著連梁剛度將減少。

圖8 荷載沉降曲線

圖9 不同連梁剛度下的軸向力

4 結語

本文通過有限元數值模擬，驗證了連梁樁結構的承載特性和有限元結果的可靠性，改變了連梁的寬度、長度和剛度，分析了不同參數對結構承載力和受力形式的影響，并對結構進行了優化分析，主要結論如下。

連梁樁結構的荷載-沉降曲線略有變化。與樁群基礎相比，其承載能力有很大提高，在198．52kPa 的荷載下，沉降量減少了45．10%。連梁樁基結構的軸向力有明顯的驟減，連梁處的軸向力遠大于樁基的軸向力，顯示出良好的豎向承載能力。在豎向加載過程中，連梁產生了較大的拉力來傳遞和分配荷載。

連梁越寬，沉降越小，垂直軸向力越高，由于“墻群效應”，連梁的拉力越小。梁的寬度不宜過大，應控制在3．5 倍樁徑以內。

連梁樁結構的長度越長，沉降量越小，承載力越大，梁的垂直軸力越大，水平軸力越小。梁長與樁距相同，梁樁結構過小時，受“樁群效應”的影響較大。連梁的長度應控制在不小于4．5 倍樁徑，6 倍樁徑以上時可以不考慮“樁群效應”。