航空發動機氣動失穩檢測管路設計研究

詹軻倚, 劉有云, 陳 航, 耿 佳

(1.中國航發貴陽發動機設計研究所,貴州 貴陽 550081; 2.清華大學 航空發動機研究院,北京 100089;3.空軍裝備部駐貴陽地區第二軍事代表室,貴州 貴陽 550081; 4.西安交通大學 機械工程學院,陜西 西安 710049)

航空發動機失穩通常可分為失速和喘振[1],失速分為葉片失速和旋轉失速。葉片失速指整個葉片同時發生失速現象,該現象較少發生。旋轉失速指某些葉片軸向通道位置氣流量減小,氣流產生葉背分離,形成與葉片旋轉的失速團現象,較為多見。失速發生時,壓縮部件可以與下游部件進行匹配工作,僅流量、壓比和效率同時有較大程度的下降[2],對航空發動機危害不大。喘振發生時氣體流量和壓力將出現低頻振蕩,壓縮部件無法再與下游部件匹配,造成航空發動機性能降低,渦輪熱負荷增加,燃燒室穩定工作范圍縮小,從而損害發動機結構完整性,最終威脅飛行安全[3],喘振以是否出現“氣流回流”現象來劃分,可分為經典喘振和深度喘振,出現“氣流回流”則為深度喘振[4]。

航空發動機失穩時,轉速、渦輪后溫度、截面氣流壓力、整機振動均會發生一定程度的變化。相對于其他參數,截面壓力參數具有測量簡便、區分度明顯和實時性良好等優點,使其成為失穩研究和判別的主要測量參數。在該研究領域,壓力變化率法[5-6]、時域診斷分析法[7]、統計特征自動門限法[8]、動態面控制方法[9]、小波系數重構法[10]、李雅普若夫指數譜法[11]、熱力學熵理論法[12]、時序信號進行目視檢查法[13]、壓力波能量的分析法[14]、基于兩點相關函數法[15]、微分變化率法[16]等多種失穩判別方法均將截面壓力選定為測量參數。無論基于何種研究目的或使用場景,測壓管路作為連接測壓點和傳感器的“通道”,在設計和試驗工作中都是不可忽視的環節。然而現有的失穩判別方法對測壓管路設計確鮮有提及。筆者所在單位在某新型渦扇發動機研制過程中,曾遇見過因測壓管路設計不合理導致喘振特征值異常的案例,原因為測壓管路長度差異較大使得總、靜壓相位差過大,導致“喘振”虛警,成為工程實踐中的難點問題。

針對航空發動機喘振與旋轉失速的特點,探討了試驗測量和機載測量失穩判別信號測量方法,兩種使用場景均須考慮測壓管路響應頻率,分析了氣動失穩檢測對測壓管路的影響和需求,由管路和傳感器容腔構成的測壓系統單自由度二階模型,研究了管路氣動耦合頻率與聲速、管路長度、管路內徑、傳感器容腔的關系,提出了發動機喘振測壓管路設計方法。結果顯示,將測壓管路經本文所述的方法校核后,未再發生虛警且能夠準確判別出發動機喘振,可用于指導航空發動機失穩檢測管路設計和工程實踐。

1 失穩判別信號測量方法

1.1 試驗測量

試驗測量領域側重于對失穩機理和數據特征的研究,通常采用多組壓力傳感器對發動機多截面壓力同時進行測量。例如魏灃亭等[17]對壓氣機第1級靜子通道壓力進行時頻分析時,所采用的傳感器響應頻率達到了150 kHz,且采用了5 kHz和10 kHz兩種數據采集率。單曉明[18]為研究渦軸發動機壓氣機內流場非穩定壓力信號,在壁面沿周向布置了7支Kulite動態壓力傳感器。其傳感器響應頻率優于200 kHz,數據采集頻率可達1 MHz。

試驗測量通過分析存儲的原始數據實現對失穩現象的研究,其對傳感器響應頻率和數據采集頻率均有較高要求,然而上述工作均未涉及測壓管路的影響研究,而試驗過程中若未考慮測壓管路的頻率響應,將使得測壓管路在研究中成為提升分析頻率范圍的“短板”,若管路容腔過大,將“濾除”原始信號的高頻特征,導致高頻采集和記錄成為“徒勞”。

1.2 機載測量

1.2.1 機械式測量

XYC-3型傳感器[19]是機械式測量方法所采用的一種典型傳感器結構,如圖1所示。其通過毛細管將壓氣機后壓力作用于壓差膜片兩端。當壓力急劇變化時,壓差膜片處由于壓力不均衡產生位移,通過連桿和頂桿等機械結構使得微動開關動作,從而將該開關信號輸送至發動機數字調理器中以獲得失穩特征信號。該方法實施簡單,但當壓氣機后壓力變化稍大時容易出現誤動作,且頻率響應較低,無法檢測出旋轉失速等高頻信息,因而通用性較差,目前已經趨于淘汰。當測壓管路變化時應考慮因壓力脈動增強/衰減導致的與壓力膜片的匹配性的問題。

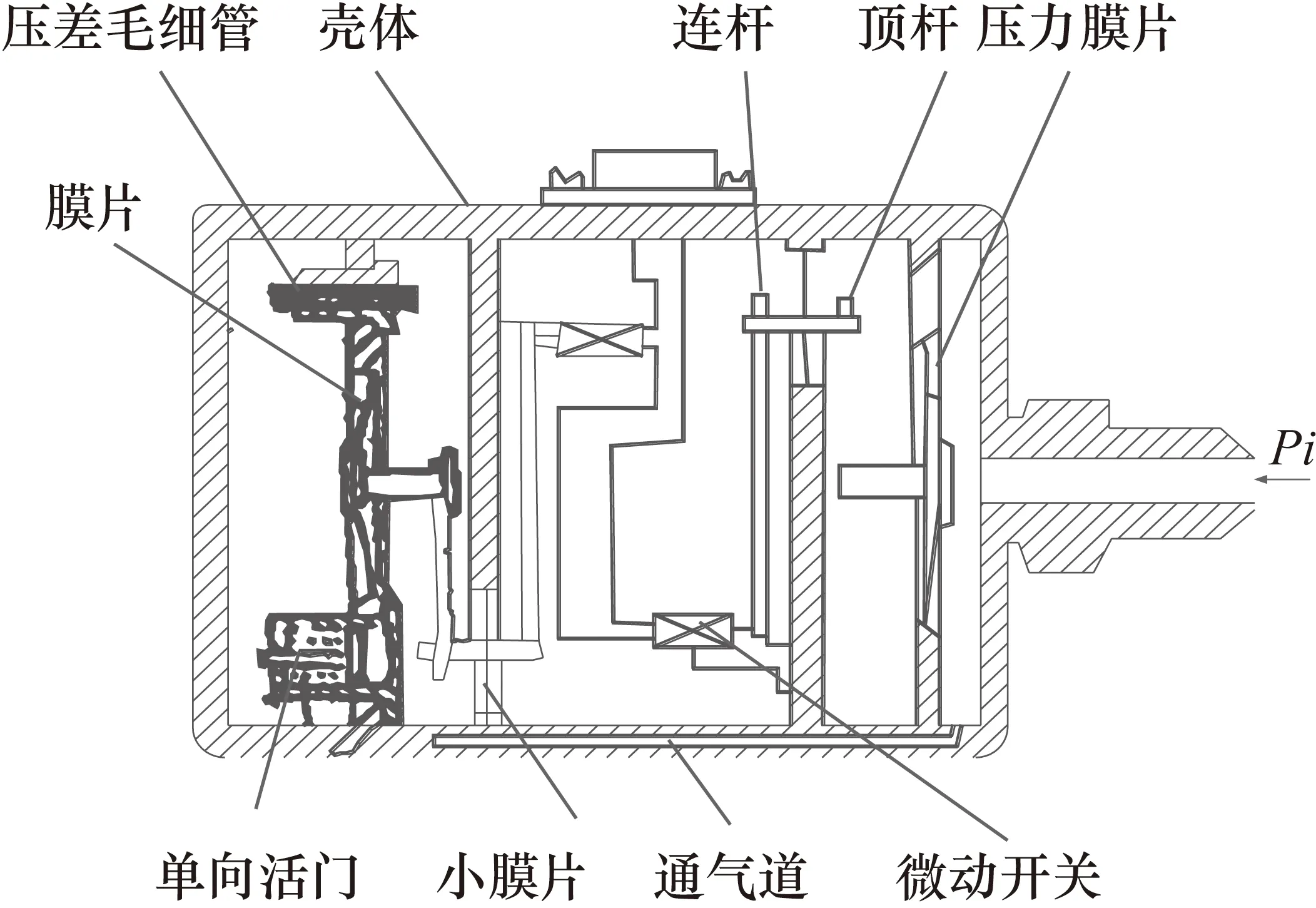
圖1 XYC-3型傳感器結構示意圖

1.2.2 模擬式電路式測量

模擬電路式喘振測量方法在控制器中實現,式(1)為傳感器輸出信號值與被測壓力的關系式。測量目標壓力經測壓管路傳導后作用于傳感器中的薄膜上。壓力相對變化即可轉化可為電壓增量,如式(2)和式(3)所示。該方法可根據發動機狀態設置閾值,使用更為靈活,缺點是在高壓比發動機中,較難解決壓力范圍與膜片敏感度的技術矛盾。

U=K-In(P)

(1)

(2)

(3)

式中:U為傳感器輸出電壓;K為與傳感器特性相關的常數;P為傳感器感受的壓力。

為解決該技術矛盾,隨即發展出了一種壓差式氣動失穩檢測方法。其通過“T型”感頭將壓氣機后總壓(P3t)和壓氣機后靜壓經測壓管路傳輸至喘振壓差傳感器膜片兩側,如圖2所示。“T型”感頭迎著氣流方向測得主流道總壓,背氣流處將形成“回流渦”,如圖3所示。背氣流處軸向、周向速度均接近0,壓力接近于感頭處氣流的靜壓。而“T型”感頭的作用之一是盡可能保證總、靜壓兩側氣流通道長度相同。

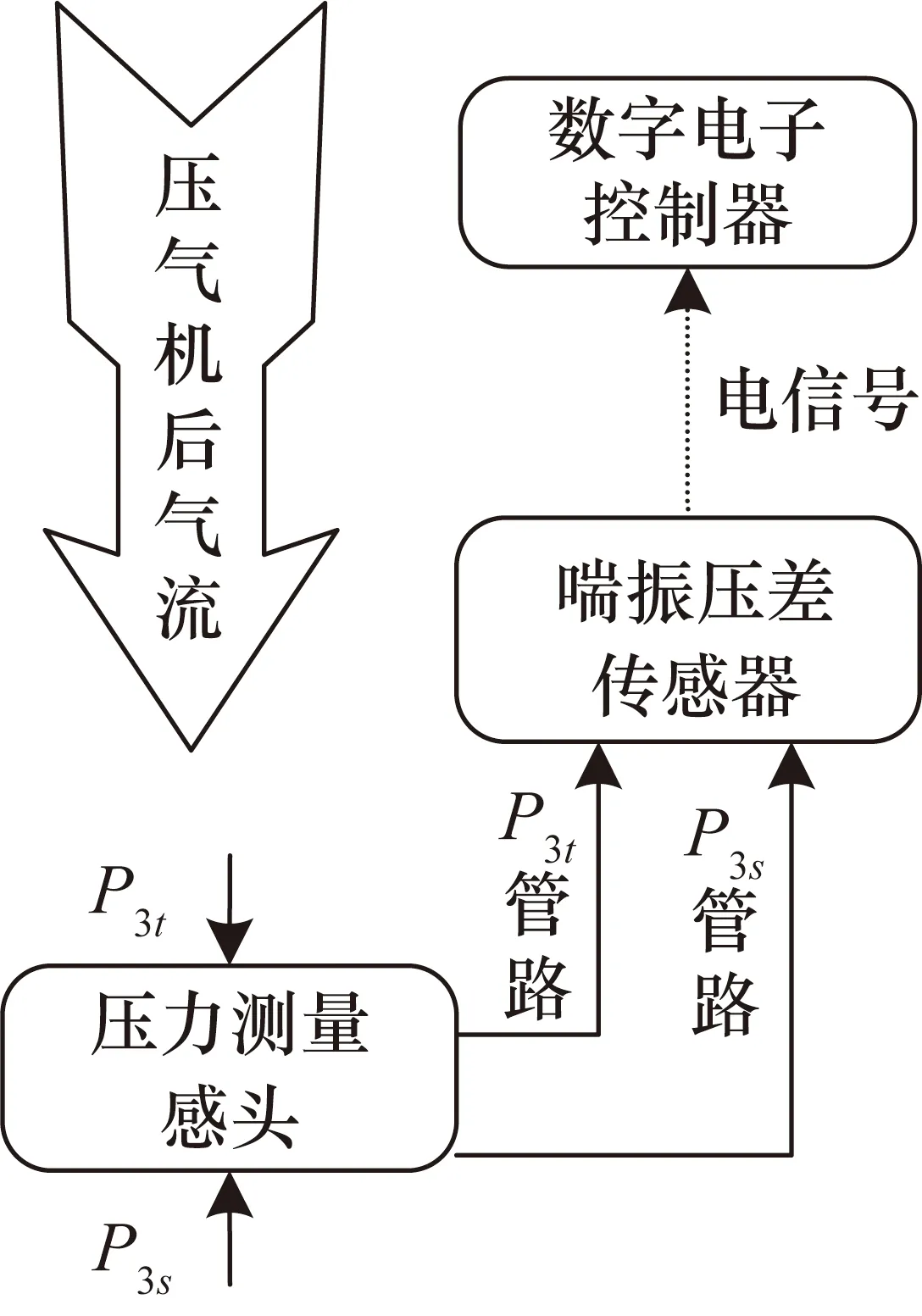
圖2 壓差式喘振測量系統組成

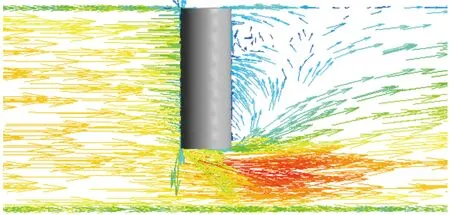
圖3 “T型”感頭流場仿真云圖

喘振壓差傳感器受感器結構如圖4所示。當總壓與靜壓差值變化時,受感器敏感元件產生彈性形變,使中心桿上下運動,帶動彈簧片組合的銜鐵上下運動,改變了磁路氣隙,從而改變了輸出電壓。該類傳感器輸出頻率可達到5～10 kHz。當測壓管路變化時應考慮總、靜壓管路長度差異導致的相位差現象和因壓力脈動效應增強/衰減導致的與壓差傳感器中受感元件的匹配性問題。

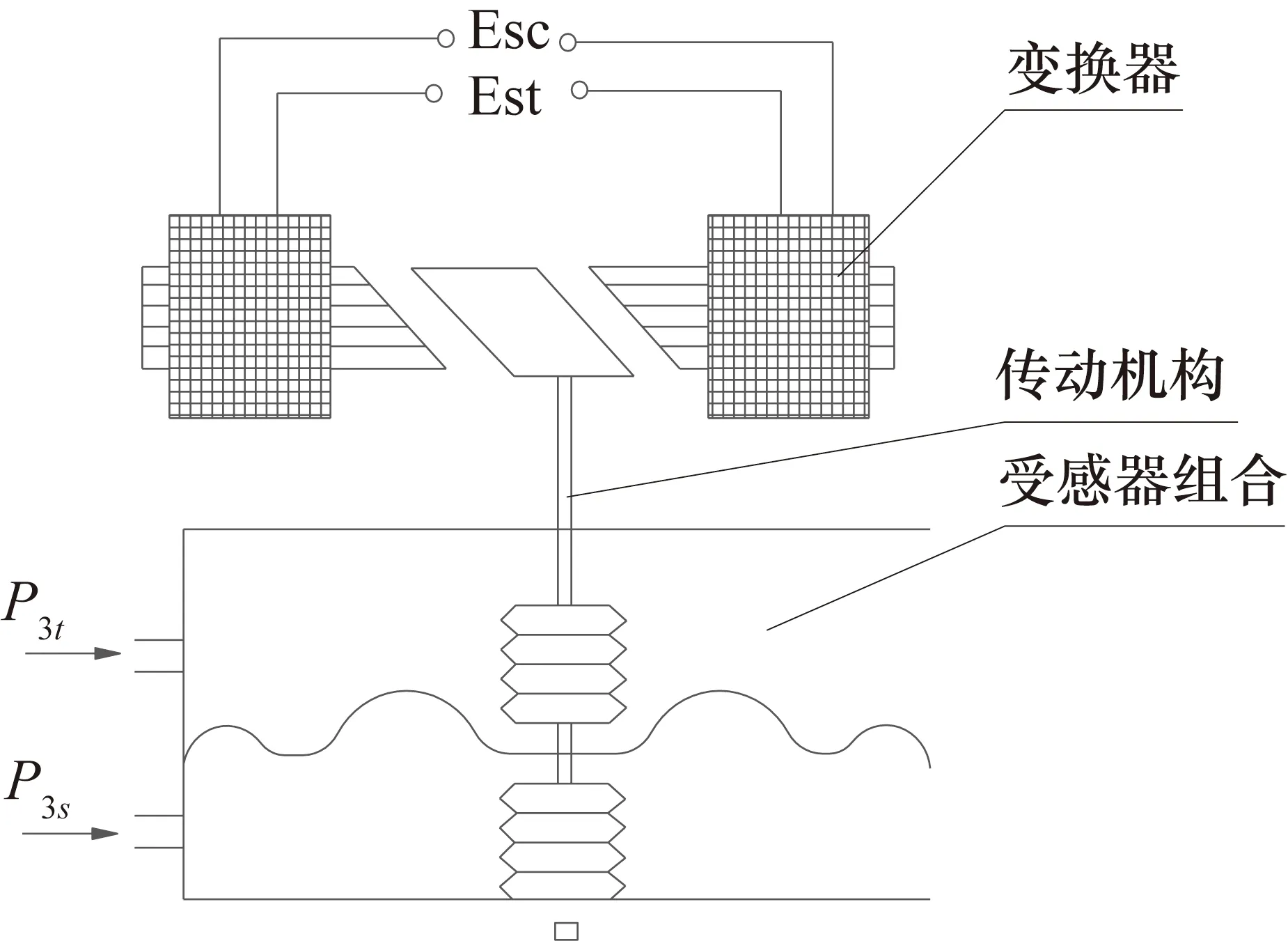
圖4 喘振壓差傳感器結構圖

1.2.3 數字電路式測量

數字電路式測量方法通過響應頻率高的壓力傳感器測量,由數字電子控制器對采集而來的數據進行處理,隨著傳感器和數字電子技術發展,愈發展現出其靈活的一面。例如王玉東[5]將機載測量的壓氣機出口靜壓和轉子轉速參數,建立了基于一階與二階的喘振檢查方法,經發動機核心機與數十次整機驗證有效。李小彪等[20]對發動機壓氣機后總壓變化率進行了分析,綜合考慮了發動機減速、二次起動、電壓白噪聲、瞬時電氣干擾對喘振判別的影響,設計了一種基于壓力變化率的喘振判別方法,對地面試驗和飛行試驗的數據進行了檢驗,沒有發生漏判和誤判。該方法較為靈活,可通過軟件算法設計不同判別方法,而不用對硬件進行更改,根據發動機狀態設計不同閾值,無須采用額外測壓感頭,較為輕便。同時,隨著數字電子控制器中處理能力的提升,該方法將成為主動防喘技術的重要支撐。當測壓管路變化時因測壓管路固有頻率變化,應考慮測壓管路長度差異使得壓力脈動增強/衰減與判定方法的匹配問題。

測壓管路是機載測量過程中的重要環節,目前針對測壓管路的設計方法僅包括布局設計、接頭設計和支承設計等基本步驟,未將測壓管路和失穩測量進行耦合分析。

1.2.4 頻率響應需求

測壓管路的作用是為氣體從測壓點流動到傳感器提供“氣流通路”。用于失穩判別的壓力測量管路與發動機上其他截面或其他作用的壓力測量點不同,能夠響應動態壓力變化。旋轉失速的壓力頻率與壓氣機轉速及葉片構型有關,通常在一百至數百Hz區間內;喘振頻率和發動機容腔大小相關,通常在幾至數十Hz區間內,通常來說喘振頻率較失速頻率低。進入和退出旋轉失速狀態的特征也與壓力信號的頻率有關,例如文獻[17]中,某型發動機在壓氣機逼喘情況下進入和退出旋轉失速狀態的特征為壓力信號27 Hz頻率分量的漲落。工程上可通過式(4)確定管路頻率要求,使其能夠滿足失速和喘振的測壓頻率需求。

(4)

式中:n為旋轉部件物理轉速,r/min;A為“旋轉失速團”引起的壓力脈動頻率系數,通常可取0.6[21]。對于機載測量中關注的喘振,該值可設定為0.3。

當管路頻率較低不能滿足測量需求時,測壓管路將成為整個系統的短板,即使采用采樣頻率較高的采樣設備也將成為徒勞;當管路頻率能夠滿足測量需求時,再增加采集系統的能力才有意義。

2 測壓管路模型建立與分析

壓力測量均可等效為測壓管道簡化圖,如圖5所示。其中,Pi為壓力測點處進口壓力;l為測壓管路長度;d為測壓管路直徑。傳感器可簡化成在彈簧支撐下的質量,其中,V為傳感器容腔體積;PV為傳感器測得的壓力。

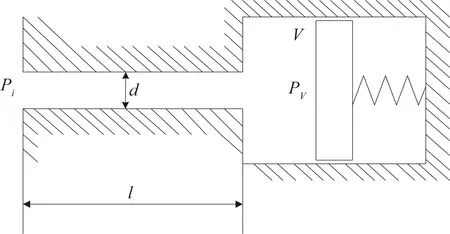
圖5 測壓管道簡化圖

現代傳感器頻率響應遠優于管路系統,可將傳感器頻率響應設定為理想狀態,則對管路系統的頻率響應問題研究可明確為管路系統入口壓力Pi與傳感器端壓力PV之間的變化關系。在滿足一定條件下,信號可分解成各規格正弦信號的疊加。假設入口壓力Pi正弦變化,管口壓力變化將以壓力波形式以聲速c傳遞,如果管路長度l遠小于波長,則壓力分布可忽略,管路內各個截面壓力可認為相等,從而可把管路內的流體運動看作為圓柱形整體運動。管路內氣體可看作有質量的剛性柱體。傳感器容腔體流體無出口,流速較小,流體的加速度作為速度的導數,更是高階微量,可忽略不計,因而傳感器容腔內的流體慣性和傳感器容腔的慣性質量可以不予考慮。然而其壓縮性不可忽略,因為傳感器容腔體流體體積變化須由管路內流體補償,傳感器容腔體積的微小變化將引起管路氣體高速流動,產生較為可觀的彈性力,故傳感器容腔可看作有彈性無質量的理想彈簧。

綜上所述,管路內的流體可簡化為一個有質量的剛性柱體,傳感器容腔可簡化為一個沒有質量的彈簧。考慮到氣體流動過程中的摩擦阻尼,測壓管路構成了一個典型的單自由度二階模型,如圖6所示。

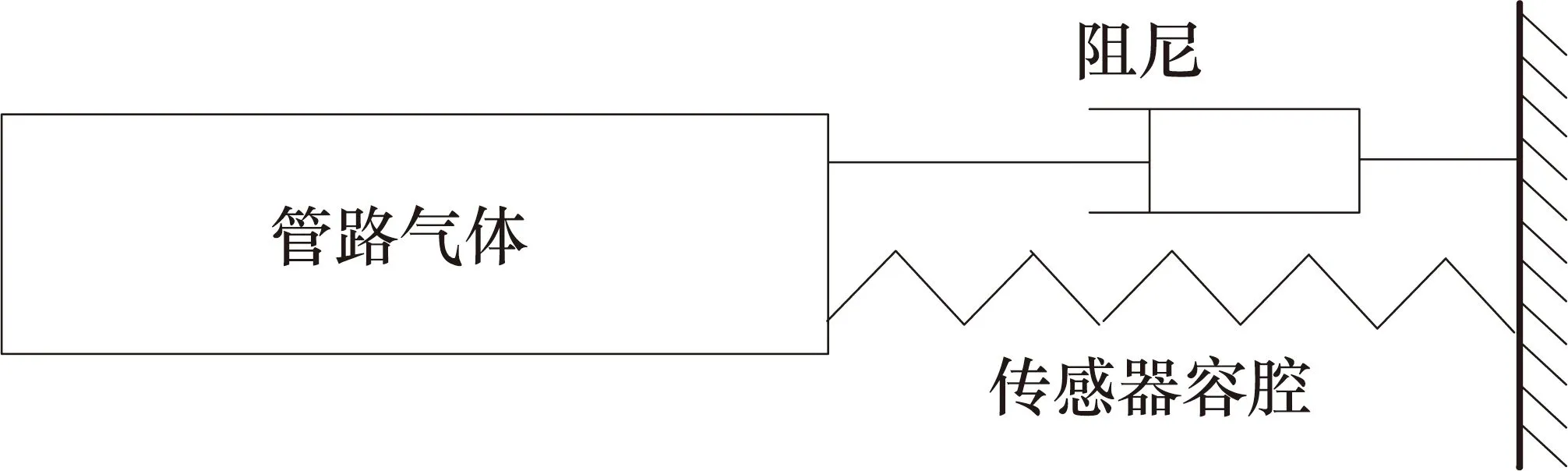
圖6 壓力測量等效模型

為進一步進行分析,做出如下假設:

① 管路內流體不可壓縮。

② 傳感器容腔內流體可壓縮,流速和慣性質量可忽略。

③ 管路及傳感器容腔外壁為剛性。

④ 傳感器的頻率響應是理想的,慣性質量可忽略。

⑤ 管路內流動是層流,摩擦阻力符合泊肅葉定律。

根據氣體體積彈性模量定義,可得傳感器容腔氣體體積變化率與傳感器容腔體壓力變化率的關系為

(5)

傳感器容腔流體體積的變化應由管路內流體進行補充,即

(6)

將式(5)代入式(6),則有

(7)

層流情況下,根據泊肅葉定律,摩擦阻力為

(8)

對管路中流體建立微分方程為

(9)

將式(7)和式(8)代入式(9)得

(10)

式(10)為典型的單自由度系統微分方程,較標準式(11)可得到系統無阻尼固有頻率關系,如式(12)所示。系統阻尼比如式(13)所示。

(11)

(12)

(13)

式中:x為系統輸入;y為系統輸出;ωn為系統無阻尼固有頻率;ξ為系統阻尼比;d為管道內直徑;μ為流體運動粘度;Ea為氣體彈性模量。

根據聲速公式(14),可將式(12)變形為式(15)。

(14)

(15)

式中:c為聲速;Vt為管路體積;V為傳感器容腔體積;l為管路長度。

式(15)明顯的漏洞為當管長l=0時,固有頻率ωn無限大,該漏洞為假設傳感器容腔內的流速可忽略不計導致的,當管路長度較長時,流體的質量不可忽略,其速度較傳感器容腔內速度大得多,因此管路中流體動能較傳感器容腔中流體大得多,此時可忽略傳感器容腔內的流速;然而,當管長l很短甚至為0時,傳感器容腔內的動能即不能忽略。

(16)

式中:le為等效管路長度;l為管路長度。

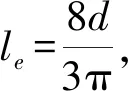
現代傳感器容腔較小,當傳感器容腔V的體積很小時,管路內流體的可壓縮性不能完全忽略不計,須在傳感器容腔體積中考慮管路的壓縮性,利用式(17)中等效體積Ve代替真實的傳感器容腔容積V。

Ve=V+Vte

(17)

同時,可采用式(18)對管路容積進行等效[22]。

(18)

式中:Ve為傳感器容腔等效體積;Vt為管路體積;Vte為考慮氣體可壓縮性的附加容積。

將式(16)～式(18)代入式(15)可得測壓系統的固有頻率為

(19)

式中:c為聲速;le為等效管路長度;Vte為等效管路體積;V為傳感器容腔體積。

通過式(16)～式(19)可根據測壓管路、傳感器尺寸對測壓系統的固有頻率進行計算,并與式(4)中測壓頻率需求進行校核。

通過式(19)一方面可對管路頻率響應進行準確計算與進一步校核,當管路長度較短時尤為重要;另一方面,可得到系統微分方程,得到系統的阻尼比,可利用其進行更為詳細的時域、頻域分析和研究。

3 測壓管路設計流程

測壓管路與航空發動機其他管路一樣,需要開展包括布局設計、接頭設計、支承設計、管路系統計算等設計工作,還需開展耐壓試驗、振動特性試驗、彎曲疲勞試驗和環境試驗等工作。根據前文所述,須對航空發動機失穩測量管路規格(長度、內徑)進行設計和校核,以滿足失穩測量的頻率響應需求。航空發功機失穩測量管路設計流程如圖7所示。

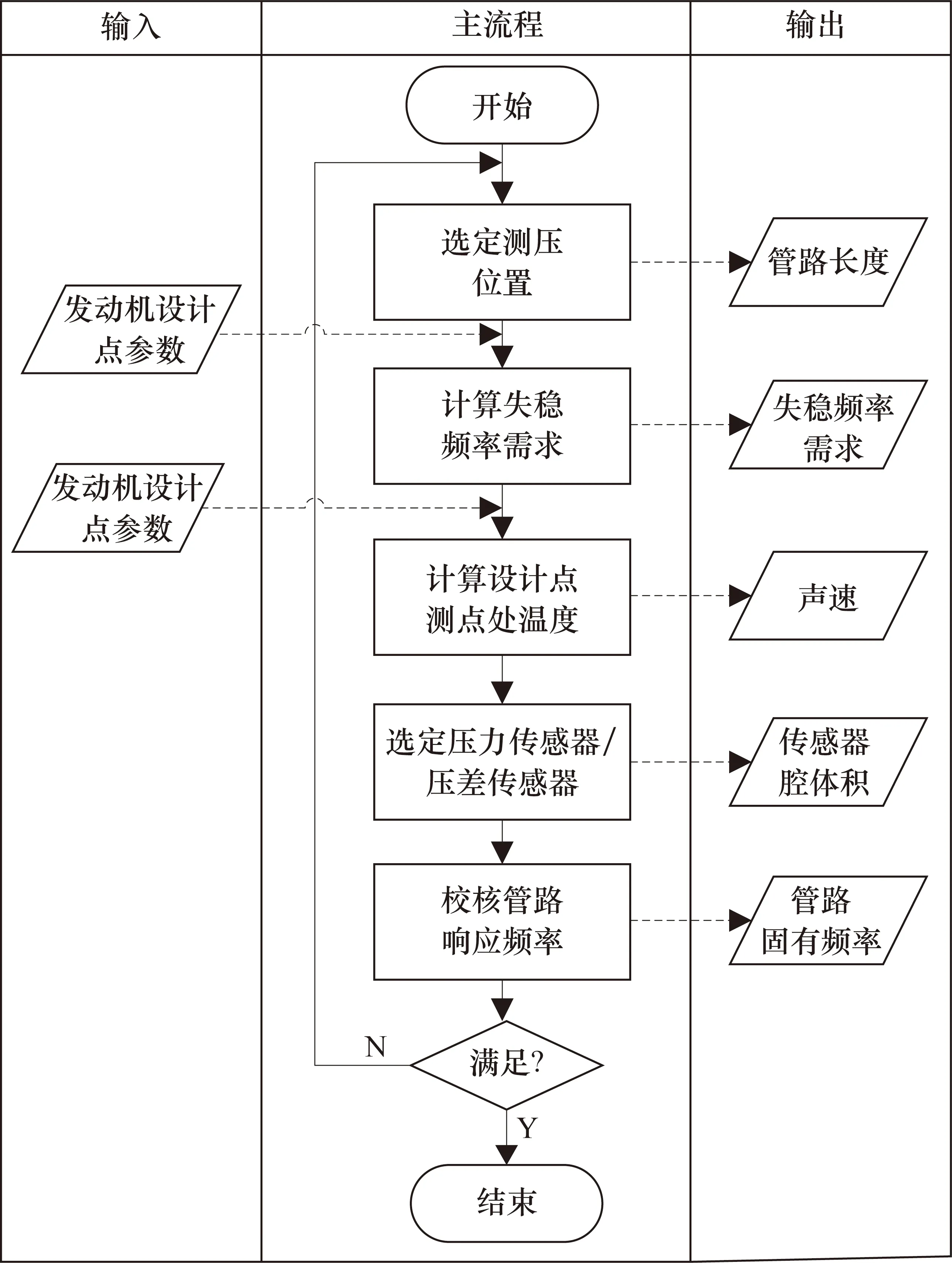
圖7 航空發動機失穩測量管路設計流程(僅針對失穩測量的頻率響應需求)

具體流程如下。

① 選定測壓位置。根據發動機失穩監測的轉子對象,選定測壓點。對于雙轉子渦扇發動機,通常選定在壓氣機后,該步驟可對管路進行初步敷設,得到管路長度。

② 計算失穩頻率需求。根據設計點轉速,根據式(4)計算失穩需求頻率f。

③ 計算設計點測點處溫度。根據發動機使用情況,確定設計點處溫度,以計算聲速c。

④ 選定壓力傳感器/壓差傳感器。根據失穩檢測要求,選定傳感器,該步驟可確定傳感器容腔體積,根據接口可初步確定管路直徑。

⑤ 校核管路響應頻率。由管路長度l和管路內徑d根據式(15)得到等效管長le與管路體積,由聲速c、管路等效管長度le,等效管路體積Vte、傳感器容腔體積V根據式(19)計算管路固有頻率fn

⑥ 將計算得到的管路固有頻率fn與失穩測量頻率需求f比較,為保證幅頻響應要求,需滿足式(20)要求。

fn≥2f

(20)

若不能保證,應對失穩測量系統進行重新設計,根據式(19),可從增大管路長度或直徑,減小傳感器容腔體積等方面進行改善。

4 算例分析

發動機壓氣機設計轉速為15000 r/min,須測量壓氣機后壓力,該測壓點處設計狀態溫度為200 ℃,在該溫度下氣體密度為0.746 kg/m3,運動粘度為2.59×10-5Pa·s,選定硅壓阻式傳感器,傳感器容腔體積為5.324×10-9m3(2.2 mm×2.2 mm×1.1 mm),管路直徑為6 mm(內徑,下同),初步敷設管路長度為500 mm。分析管路是否能夠滿足失穩檢查要求。

根據已知條件,依次計算得到以下信息。

① 失穩測壓頻率需求:f=150 Hz;

② 使用包線內聲速:c=453 m/s;

③ 等效管路長度:le=505.09 mm;

④ 等效管路體積:Vte=5.732×10-6m3;

⑤ 傳感器容腔體積:V=5.324×10-9m3。

根據式(13),計算得到管路的阻尼比為0.0689,根據式(19),計算得到管路的測壓固有頻率為224.11 Hz,固有角頻率為1407.4 rad/s,不能夠滿足大于2倍失穩頻率(300 Hz)的要求。為了滿足要求,管路直徑和傳感器容腔保持不變的條件下,經反向計算,應將管路長度設置在374 mm以內。目前傳感器容腔比管路容腔小,通常僅為管路容腔體積的2%以內,工程中可采用“四分之一波長法”對失穩測壓系統固有頻率進行初步估計,即響應頻率為聲速與四倍管長的商。如上例中,采用“四分之一波長法”計算得到的固有頻率為226.5 Hz,與通過式(19)計算的固有頻率相差1%以內。

為進一步論證“四分之一波長法”在各規格測壓管路上的誤差情況,設定傳感器容腔體積為10×10-9m3,做出管長、管徑與誤差關系,設置管路長度范圍為50～1500 mm,管路直徑為6 mm,8 mm,10 mm三種規格,管路規格與相對誤差關系如圖8所示。從圖8中可知,采用“四分之一波長法”得到的管路固有頻率計算值相對于通過式(19)的計算值偏大。管路直徑一致的條件下,以通過式(19)中計算的管路固有頻率為基準,定義采用“四分之一波長”法計算得到的管路固有頻率與之相比為估算相對誤差。隨著管路長度增加,估算相對誤差減小;管路長度一定的條件下,隨著管路直徑增加,估計相對誤差減小;若管路長度大于260 mm,三種規格管路估計誤差均小于2%,采用“四分之一波長法”對失穩測壓系統固有頻率進行估計較為準確。在工程應用中,應建立對“四分之一波長”法的總體認識,估算法較實際值偏大,且管路長度越短,該誤差越大。如管路長度為50 mm時,誤差約為11%,管路長度為100 mm時,誤差約為5%,管路長度為200 mm時,誤差約為3%,可采用與管路長度相關的修正系數對“四分之一波長”波長法的結果進行進一步修正。

圖8 管路規格與相對誤差關系

根據管路固有頻率與管路長度、管路直徑的關系,在傳感器體積不變的情況下,管路長度越短,測壓系統的頻率越高;同樣管路長度下,管徑越大導致等效管路長度越長,式(19)中根號內數值雖然越大。因為目前傳感器容腔體積遠小于管路體積,故等效管路增長對測壓頻率起到主導作用,故管路內徑不應過大,另一方面由于管路爆破壓力限制、管路柔性、附面層效應、與傳感器接口的匹配,測壓管路直徑不宜過細(例如Ф4 mm以下),因此工程上以Ф(6～8) mm為宜。在滿足傳感器布置的情況下(須綜合考慮振動、避免溫度、可維護性等要求),測壓管路越短對失穩測量越有利。

在實際工程實踐中,若設計管道不能滿足失穩測量系統的頻率響應需求,縮短管長的方式對提高系統的響應頻率最為有效。

5 結束語

基于失穩測量的運用場景,分析了測壓管路對氣動失穩檢測的影響和需求,建立了由管路和傳感器容腔構成的測壓系統的單自由度二階模型,研究了管路氣動耦合頻率與聲速、管路長度、管路內徑、傳感器容腔的關聯關系,并根據工程經驗給出了管路規格設計流程。

① 針對發動機失穩測檢測,其管路規格應滿足失穩頻率響應的設計要求,導管過長一方面將導致測壓端不能反映高頻的動態壓力的變化,另一方面過長的管路將使得壓力波傳遞時間過長,影響失穩判定方法的快速性。在試驗研究領域,應盡量減小壓力測壓管路長度,以保證數據能夠有效反映壓力的動態變化。工程上可利用“四分之一波長法”對測壓管路固有頻率進行估計,再按其設計流程實施進一步校核計算,在后續的工作中,可對管路規格對失穩現象判別進行進一步研究。

② 在機載運用領域,應根據發動機設計點對管路進行頻率校核。若采用壓力測量方法,應盡量將管路布置在測點附近,若采用壓差式失穩測量方法,除了單根管路規格要滿足需求外,兩根測壓管路長度和管型應盡量保持一致,以免壓力在不同管路中傳遞時間不同,導致測量端產生相位差,影響失穩的判別,專利中提出的“心型”對稱結構[23]可作為一種優選方案。

③ 在失穩檢測管路方面,由于航空發動機使用過程中高度變化,空氣中冷凝現象也應注意,可進一步開展失穩測壓管路防冰相關研究和設計。