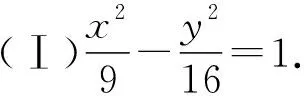順應“三新”趨勢探索變式教學模式
——數學變式征集活動解析幾何專題試題選登

(作者單位 姓名:江西上饒余干第一中學 鄒榮華)

(作者單位 姓名:甘肅省嘉峪關市第二中學 彭長軍)

(作者單位 姓名:江西上饒余干第一中學 葉新波)

(作者單位 姓名:陜西省寶雞市麟游縣中學 韓紅軍)

(作者單位 姓名:江西上饒余干第一中學 葉新波)

(作者單位 姓名:河北定州中學 趙偉娜)

【精選變式題組】

【母題1】(2022·江西余干一中)已知⊙O的方程為x2+y2=4,過M(4,0)的直線與⊙O交于A,B兩點,則弦AB的中點P的軌跡方程為________.

【變式1】(知識變式)將母題中的“圓”換為“橢圓”

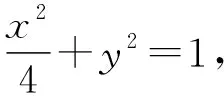
【變式2】(方法變式)將過圓外一點變為過圓內一點

已知⊙O的方程為x2+y2=25,過M(4,2)的直線l與⊙O交于A,B兩點,則弦AB的中點P的軌跡方程為________.

【變式3】(綜合變式)變圓中點弦為橢圓中點弦,變單空為雙空,定點與兩交點的位置由同側變為異側,同樣可以用點差法處理問題.

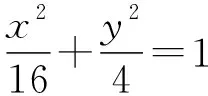
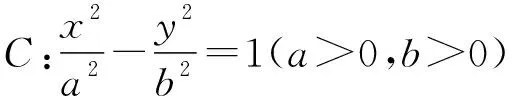
(Ⅰ)求雙曲線C的標準方程;

(Ⅱ)設Q為雙曲線C右支上的一個動點,在x軸上是否存在定點M,使得∠QFM=2∠QMF?若存在,求出點M的坐標;若不存在,請說明理由.

【變式1】(知識變式)將“在x軸上是否存在定點M”變為“在x軸的負半軸上是否存在定點M”

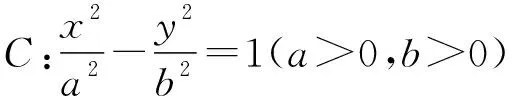
(Ⅰ)求雙曲線C的標準方程;

(Ⅱ)設Q為雙曲線C右支上的一個動點,F為雙曲線C的右焦點,在x軸的負半軸上是否存在定點M.使得∠QFM=2∠QMF?若存在,求出點M的坐標;若不存在,請說明理由.

【變式2】(知識變式)命題背景由雙曲線變為橢圓,同為考查角度的兩倍關系.

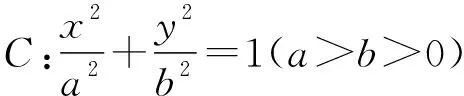
(Ⅰ)求橢圓C的方程;

【變式3】(綜合變式)變換為傾斜角互補關系,探究定點.

已知圓C1:(x+5)2+y2=36,點C(5,0),點M是圓C1上的動點,MC的垂直平分線交直線MC1于點P.

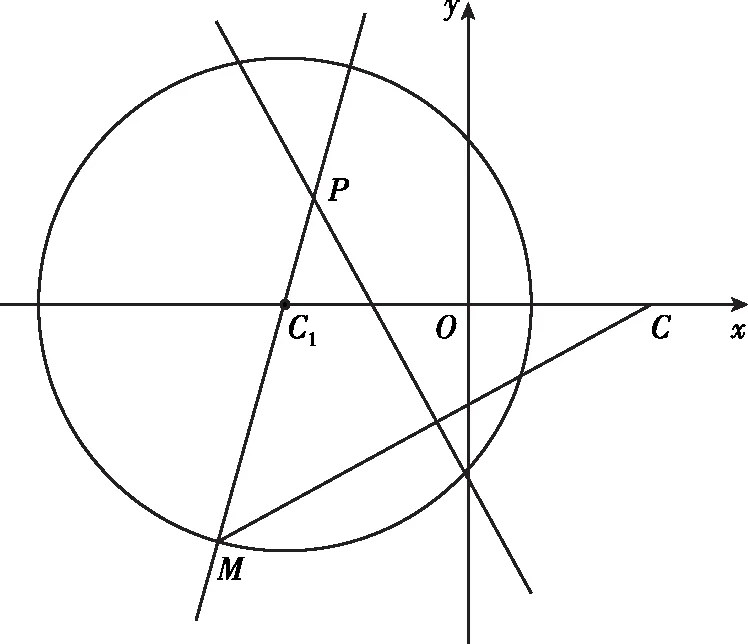
(Ⅰ)求點P的軌跡方程C2;

(Ⅱ)過點N(4,0)的直線l交曲線C2于A,B兩點,在x軸上是否存在點G,使得直線AG和BG的傾斜角互補?若存在,求出點G的坐標,若不存在,請說明理由.

【母題詳解及答案】

【母題1】【解題策略】本題考查圓中弦的中點軌跡問題,數形結合思想的應用

解法1:P為弦AB的中點→OP⊥PM→P在以OM為直徑的圓上→求解即可;

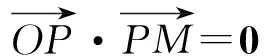
解法3:點差法→kAB=kPM→求解即可;

解法4:直線AB與圓聯立求解→用參數表示點P坐標→消參即可

【解題思路】

【解法1】

點撥:利用圓中弦的中點得出垂直,從而構造外接圓進行求解.

連接OP,由圓的性質可知OP⊥PM,如圖所示,

所以點P的軌跡是以OM為直徑的圓且在⊙O內的部分,

以OM為直徑的圓的方程為

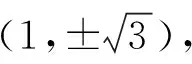
結合圖形可知所求軌跡方程為(x-2)2+y2=4(0≤x<1).

【解法2】

點撥:由圓的性質得垂直,利用垂直向量列方程求解.

連接OP,由圓的性質可知OP⊥PM,設P(x,y).

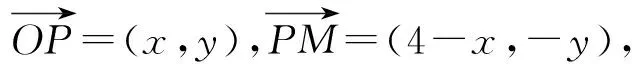
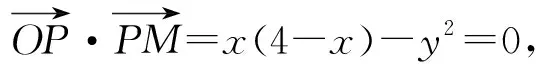
因為點P在⊙O內,所以點P的軌跡所在的圓在⊙O的內部,所以0≤x<1,

故所求軌跡方程為(x-2)2+y2=4(0≤x<1).

【解法3】

點撥:利用點差法列方程求解.

設P(x,y),A(x1,y1),B(x2,y2),

因為點A,B在⊙O上,所以x12+y12=4 ①,

x22+y22=4 ②.

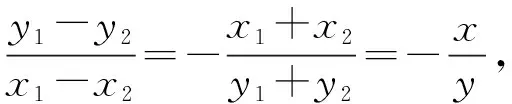
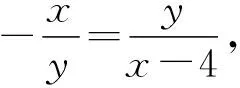
化簡得(x-2)2+y2=4.

因為點P在⊙O內,所以點P的軌跡所在的圓在⊙O的內部,所以0≤x<1,

故所求軌跡方程為(x-2)2+y2=4(0≤x<1).

【解法4】

點撥:直線的方程與圓的方程聯立,用參數表示點P,再消參得軌跡方程.

設P(x,y),A(x1,y1),B(x2,y2),

易知直線AB斜率存在,設直線AB的方程為y=k(x-4),代入x2+y2=4得

(1+k2)x2-8k2x+16k2-4=0,

消去k得(x-2)2+y2=4,

故所求軌跡方程為(x-2)2+y2=4(0≤x<1).

(作者單位 姓名:江西上饒余干第一中學 鄒榮華)

(作者單位 姓名:江西上饒余干第一中學 鄒榮華)

【變式2】x2+y2-4x-2y=0.

(作者單位 姓名:甘肅省嘉峪關市第二中學 彭長軍)

【變式3】x+4y-5=0.

x2+4y2-x-4y=0.

(作者單位 姓名:江西上饒余干第一中學 葉新波)

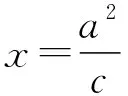
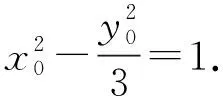
①當x0=2時,y0=±3.因為∠QFM=2∠QMF=90°,所以∠QMF=45°,于是MF=QF=|y0|=3,所以t=-1或t=5,即M(-1,0)或(5,0);

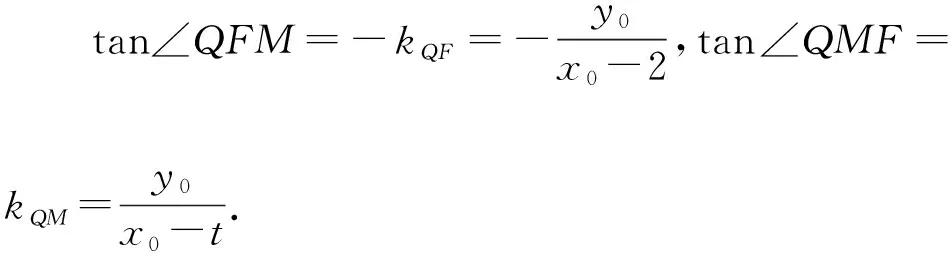
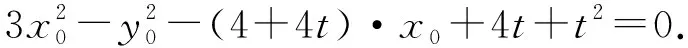
當y0=0時,t=-1,即M(-1,0)也能滿足∠QFM=2∠QMF.

綜上,存在滿足條件的點M,其坐標為(-1,0).

(作者單位 姓名:陜西省寶雞市麟游縣中學 韓紅軍)

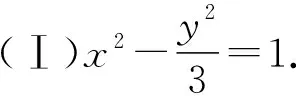
(Ⅱ)存在,m(-1,0).

(作者單位 姓名:陜西省寶雞市麟游縣中學 韓紅軍)

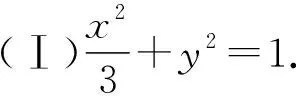
(Ⅱ)存在,定點P(0,1).

(作者單位 姓名:江西上饒余干第一中學 葉新波)