聚焦圓錐曲線問題中的“同構法”
——以近五年高考圓錐曲線試題為例

焦永垚

(甘肅省蘭州市第六中學)

1.問題的提出

高中平面解析幾何中的圓錐曲線問題是高考重點考查的內容,是高考考查學生核心素養的重要載體,對學生的數學運算能力有較高的要求.對于此類問題,學生通常將直線方程與圓錐曲線方程聯立,再利用韋達定理求解.但在具體解答過程中,往往計算量非常大且繁雜,使很多考生半途而廢.筆者發現,對于很多圓錐曲線高考題,如果運用“同構法”解決,可以簡化運算步驟,優化解題過程,提高解題的成功率.

2.初探“同構法”

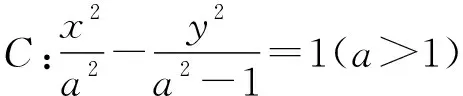
(Ⅰ)求l的斜率;

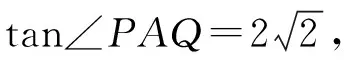
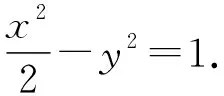
設直線PQ的方程為mx+ny=1(2m±n≠1),將點P,Q的坐標代入化簡得

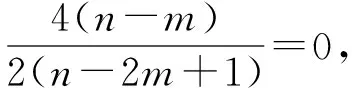
反思：上述解題過程中蘊含著一種重要的思想方法,就是“同構”思想.同構思想是高中數學中一種重要的思想方法,在數列、不等式、方程、函數及解析幾何中都有著非常廣泛的應用,是解決數學問題的一把利器.在數學上,我們把結構相同的兩個式子稱為“同構式”,把不同的數學結構轉化為相同的數學結構的思想方法稱為同構法.在解析幾何中,我們通常可以利用一些點、線所具有的“形”的共同特征構造同構式,再利用“整體消元”解決問題.此題中由于點P,Q的坐標結構相同,且都在直線l上,所以將P,Q的坐標代入l的方程,得到兩個同構式,將“k”視作主元整理成一元二次方程,再利用韋達定理得到結果.可以看出,在解析幾何中,“同構法”的中心思想就是“設而不求” “整體消元”,從而避免復雜的運算,這是解決解析幾何復雜問題的基本思路.本題中“點P,Q都在直線l上”這一“形”的“對等”性是構造同構式的關鍵.

下面筆者以近五年部分圓錐曲線高考題為例,從四個方面闡述“同構法”的解題應用.

3.“同構法”在高考圓錐曲線題中的應用

3.1 根據“圓錐曲線上的兩點在同一直線上”構造同構式

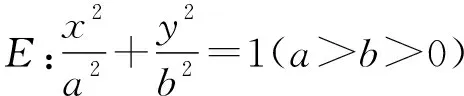
(Ⅰ)求橢圓E的方程;

(Ⅱ)過點P(-2,1)作斜率為k的直線與橢圓E交于不同的兩點B,C,直線AB,AC分別與x軸交于點M,N.當|MN|=2時,求k的值.

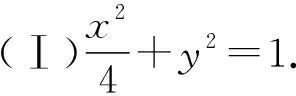
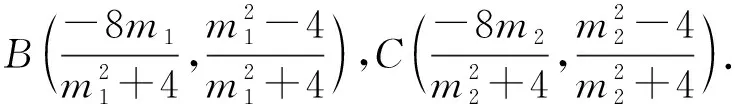
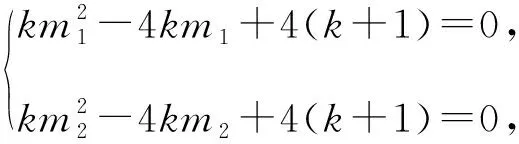
由直線AB,AC的方程可得M(-m1,0),N(-m2,0),

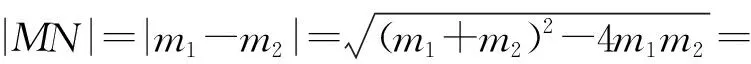
解得k=-4.

【評注】從上述解法可以看出,此題本質上與例1相同,根據“橢圓上的兩點B,C在同一直線上”構造同構式,大大簡化了運算過程.將直線AB,AC的方程設為x=m1(y-1)和x=m2(y-1)的形式而非斜截式,成功避免了對其斜率存在性的討論,從而減少了運算量.

3.2 根據“兩個點在同一圓錐曲線上”構造同構式

【例3】(2018·北京卷·19)已知拋物線C:y2=2px經過點P(1,2),過點Q(0,1)的直線l與拋物線C有兩個不同的交點A,B,且直線PA交y軸于M,直線PB交y軸于N.

(Ⅰ)求直線l的斜率的取值范圍;

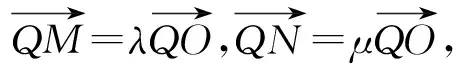
解析：(Ⅰ)直線l的斜率的取值范圍是(-∞,-3)∪(-3,0)∪(0,1).(過程略)

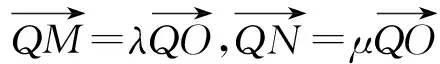
設直線l的方程為y=kx+1(由(Ⅰ)知k≠1),

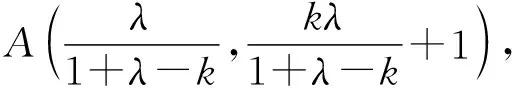
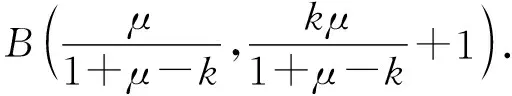
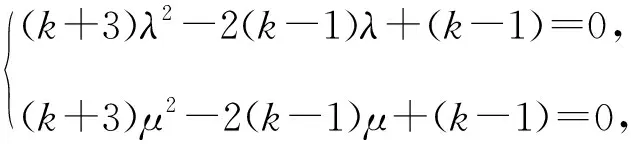
【例4】(2018·浙江卷·21)如圖,已知點P是y軸左側(不含y軸)一點,拋物線C:y2=4x上存在不同的兩點A,B滿足PA,PB的中點均在C上.

(Ⅰ)設AB的中點為M,證明:PM垂直于y軸;

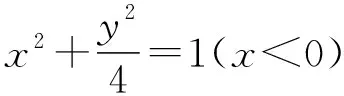
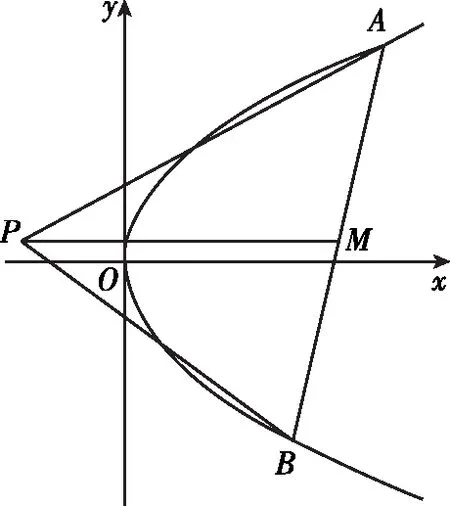
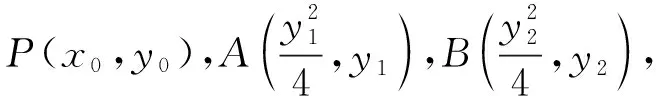
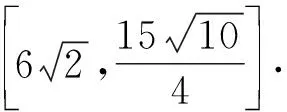
【評注】例3中的點A,B在直線l上,從而點A,B的坐標結構相同,再根據“點A,B都在拋物線C上”這一“形”的對等構造出關于λ和μ的同構方程.例4則是根據“PA,PB的中點都在拋物線C上”這一“形”的對等構造出關于y1和y2的同構方程,最后運用韋達定理完成解答.此解法擺脫了“將直線方程與拋物線C的方程聯立”的思維定式,運用“設而不求”和“整體代換”的思想優化了解題過程.

3.3 根據“兩條直線與圓錐曲線有相同的位置關系”構造同構式

【例5】(2021·全國乙卷理·21)已知拋物線C:x2=2py(p>0)的焦點為F,且F與圓M:x2+(y+4)2=1上點的距離的最小值為4.

(Ⅰ)求p;

(Ⅱ)若點P在M上,PA,PB是C的兩條切線,A,B是切點,求△PAB面積的最大值.

解析：(Ⅰ)p=2.(過程略)

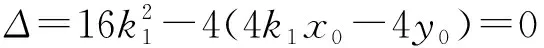
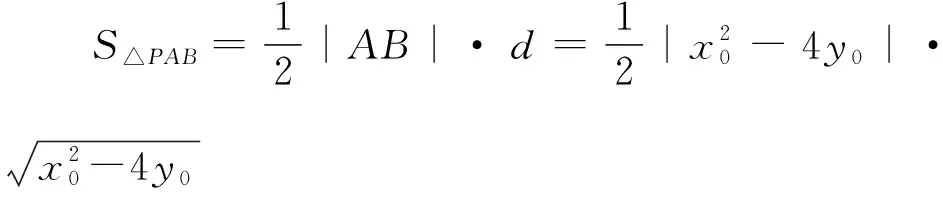
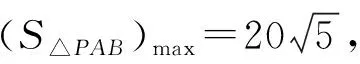
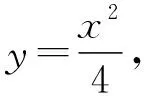
【評注】此題為拋物線中的阿基米德三角形問題,“聯立切線方程與圓錐曲線方程,消元,則Δ=0”,這是解決此類問題的通法.由兩條切線得到兩個判別式,從而構造出關于k1和k2的同構方程,再利用韋達定理求解.由于該題為開口向上的拋物線切線問題,所以也可用求導的方法解決,通過求導得到切線的斜率,再利用斜率公式得同構方程x0x1-2y1-2y0=0和x0x2-2y2-2y0=0,從而得到直線AB的方程.同為同構法,但同構法二比同構法一思維更為靈動,過程更為簡捷.

【例6】(2021·全國甲卷理·20)拋物線C的頂點為坐標原點O,焦點在x軸上,直線l:x=1交C于P,Q兩點,且OP⊥OQ.已知點M(2,0),且⊙M與l相切.

(Ⅰ)求C,⊙M的方程;

(Ⅱ)設A1,A2,A3是C上的三個點,直線A1A2,A1A3均與⊙M相切.判斷直線A2A3與⊙M的位置關系,并說明理由.

解析：(Ⅰ)C的方程為y2=x,⊙M的方程為(x-2)2+y2=1.(過程略)

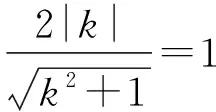
當A1,A2,A3三點都不是坐標原點時,如圖,

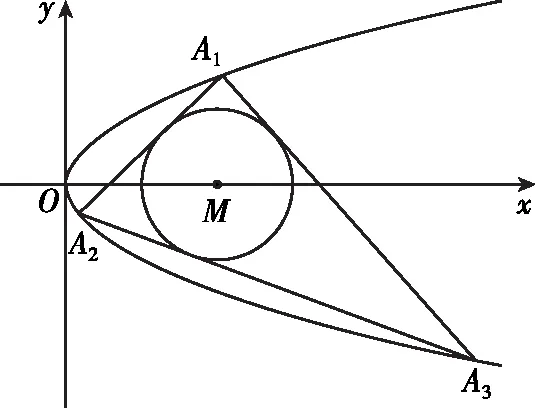
綜上所述,直線A2A3與⊙M的位置關系為相切.

【評注】此題是一道以彭賽列閉合定理為背景的高考題,由于直線A1A2和A1A3與⊙M有相同的位置關系(相切),所以它們的方程結構相同,由“圓心到直線的距離等于1”構建出點A2和A3所滿足的同構方程,思路新穎獨特,過程簡便快捷.

3.4 根據“兩條直線過同一個點”構造同構式

對于前文的例5,我們也可根據“切線PA和PB過同一點P”構造同構方程.

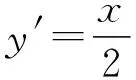
我們再來看一道以拋物線中的阿基米德三角形為背景的高考題.

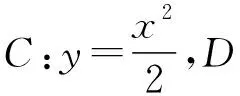
(Ⅰ)證明:直線AB過定點;

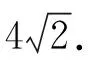
【評注】能夠用“同構法”解決的圓錐曲線高考題還有很多,如2022年浙江卷第21題、2020年全國Ⅰ卷理科第20題、2020年山東卷第22題等等,有興趣的讀者可以自己嘗試,本文不再贅述.

4.結束語