一道中考二次函數(shù)綜合題的解法探究*

合肥師范學(xué)院數(shù)學(xué)與統(tǒng)計(jì)學(xué)院(230601) 程麗雲(yún) 張新全

1 真題呈現(xiàn)

(2022 年福建省中考數(shù)學(xué)第25 題) 在平面直角坐標(biāo)系xOy中,已知拋物線(xiàn)y=ax2+bx經(jīng)過(guò)A(4,0),B(1,4)兩點(diǎn).P是拋物線(xiàn)上一點(diǎn),且在直線(xiàn)AB的上方.

(1)求拋物線(xiàn)的解析式;

(2)若ΔOAB面積是ΔPAB面積的2 倍,求點(diǎn)P的坐標(biāo);

(3) 如圖1,OP交AB于點(diǎn)C,PD//BO交AB于點(diǎn)D.記ΔCDP, ΔCPB, ΔCBO的面積分別為S1,S2,S3. 判斷是否存在最大值. 若存在,求出最大值;若不存在,請(qǐng)說(shuō)明理由.

圖1

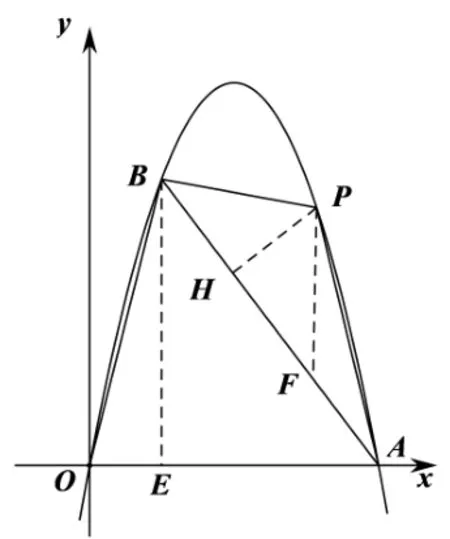
圖2

圖3

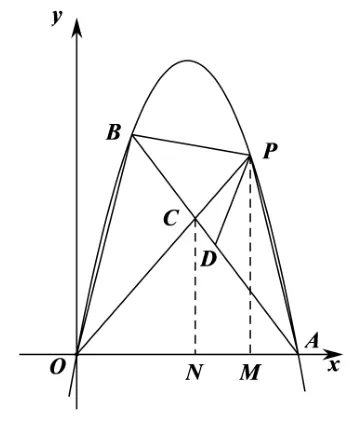
圖4

2 試題解讀

本題是2022 年福建中考數(shù)學(xué)壓軸題,以二次函數(shù)與平面幾何知識(shí)為背景,重點(diǎn)考查了與二次函數(shù)有關(guān)的面積問(wèn)題.該題涉及的數(shù)學(xué)核心概念主要有: 一次函數(shù)、二次函數(shù)的圖象與性質(zhì)、三角形的面積、銳角三角函數(shù)以及相似三角形的判定與性質(zhì)等;本題蘊(yùn)含的數(shù)學(xué)思想方法主要有: 數(shù)形結(jié)合思想、函數(shù)與方程思想、數(shù)學(xué)建模思想、轉(zhuǎn)化思想和分類(lèi)討論思想等;本題考查的數(shù)學(xué)核心素養(yǎng)主要有: 運(yùn)算能力、推理能力、空間觀(guān)念、幾何觀(guān)念和創(chuàng)新意識(shí)等.

三個(gè)小題由淺入深,層層推進(jìn). 第(1)小題涉及求二次函數(shù)解析式,主要考查待定系數(shù)法、方程思想等;第(2)小題中ΔOAB與ΔPAB具有公共邊,ΔOAB的面積是ΔPAB面積的2 倍, 則以AB為底的兩三角形的高也具有倍半關(guān)系.本題可以考慮的思路較多,最直接的方法是利用公式法分別將兩個(gè)三角形的面積用坐標(biāo)表示出來(lái),分別將兩個(gè)三角形的面積用坐標(biāo)表示出來(lái),建立等量關(guān)系即可求解出點(diǎn)P的坐標(biāo),也可以根據(jù)面積比轉(zhuǎn)化為高的比,進(jìn)而可以轉(zhuǎn)化為線(xiàn)段PC與OC的長(zhǎng)度之比,再轉(zhuǎn)化為坐標(biāo)之比,進(jìn)而求出點(diǎn)P的坐標(biāo);第(3)小題在第(2)小題的基礎(chǔ)上求面積比和的最大值,繼續(xù)深入研究三角形面積問(wèn)題.這是近兩年以來(lái)考查比較多的問(wèn)題,通常考查兩個(gè)共邊三角形面積之比的最值,利用A 字型或者X 字型的相似轉(zhuǎn)化為求線(xiàn)段的最值.而解決這一問(wèn)的關(guān)鍵是充分利用平行得到相似三角形,最終通過(guò)將三角形的面積比轉(zhuǎn)化為線(xiàn)段比,從而直達(dá)本真,化繁難為簡(jiǎn)捷,求解出比值的最值. 而學(xué)生需要實(shí)破的第一點(diǎn)是利用有公共邊的三角形同底不同高或同高不同底的性質(zhì),將面積比轉(zhuǎn)化為線(xiàn)段比或者相似比,第二點(diǎn)是斜線(xiàn)段的比值轉(zhuǎn)化成豎直或者水平線(xiàn)段之比,充分體現(xiàn)了轉(zhuǎn)化的思想,轉(zhuǎn)化過(guò)程需要學(xué)生巧妙添加輔助線(xiàn),靈活運(yùn)用數(shù)學(xué)知識(shí),這對(duì)學(xué)生的思維水平有較高要求,同時(shí)學(xué)生需要進(jìn)行細(xì)致的觀(guān)察、合理的聯(lián)想、縝密的推理,具有較大的難度和挑戰(zhàn)性.

3 解法探究

3.1 第(1)小題解法

3.2 第(2)小題解法

3.3 第(3)小題解法

思路一: 構(gòu)造“A 型”相似求解

解法1 因?yàn)镻D//BO, 所以∠DPC= ∠BOC,

解法2如圖5, 過(guò)點(diǎn)D向y軸作垂線(xiàn)DS, 分別過(guò)點(diǎn)B、點(diǎn)C向x軸作垂線(xiàn)BS和CT. 因?yàn)橹本€(xiàn)OB的解析式為:y= 4x,則可設(shè)直線(xiàn)PD的解析式為y= 4x+b,設(shè)點(diǎn)

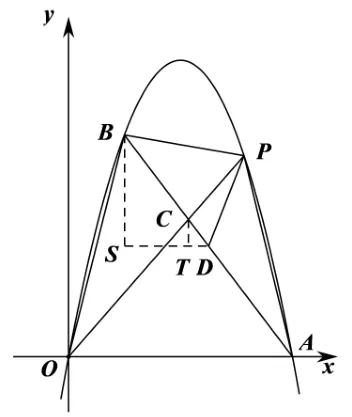
圖5

解法3如圖6, 過(guò)點(diǎn)P作AB的平行線(xiàn)l. 設(shè)點(diǎn)P的

圖6

因?yàn)閽佄锞€(xiàn)與平行線(xiàn)l只有一個(gè)交點(diǎn), 所以Δ = 0,

點(diǎn)評(píng)通過(guò)作平行線(xiàn)段構(gòu)造“A 型”相似,證明三角形相似,由相似三角形的性質(zhì)將問(wèn)題轉(zhuǎn)化為平行線(xiàn)分線(xiàn)段成比例是解決此類(lèi)問(wèn)題的通性通法.思路二: 構(gòu)造“X 型”相似求解

解法4如圖7,過(guò)點(diǎn)C作CM⊥y軸,垂足為M,延長(zhǎng)CM到點(diǎn)N,過(guò)點(diǎn)P作PN⊥CM于N. 因?yàn)镻N//OM,所

圖7

解法5 如圖8,過(guò)點(diǎn)P作PR⊥x軸,交AB于點(diǎn)R,延長(zhǎng)

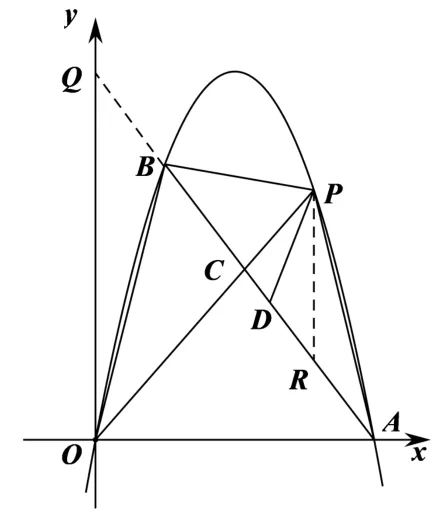
圖8

所以當(dāng)m=

解法6 如圖9, 過(guò)點(diǎn)P和O分別作AB的垂線(xiàn),垂足分別為M和N. 因?yàn)镻M//ON, 所以∠PMC=∠ODC, ∠MPC= ∠NOC, 則ΔPMC∽ΔONC, 所以因?yàn)镻M和ON是ΔABP和ΔABO的

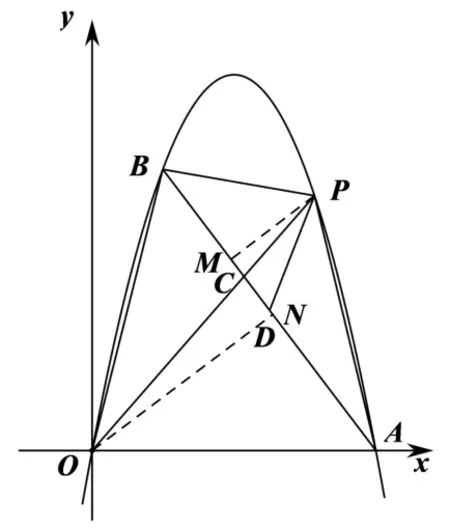
圖9

點(diǎn)評(píng)通過(guò)作垂線(xiàn)構(gòu)造“X 型”相似,利用相似三角形的性質(zhì)將問(wèn)題就轉(zhuǎn)化為求線(xiàn)段比值之和最大值,然后設(shè)未知量列方程,是求解此類(lèi)問(wèn)題的常見(jiàn)求解策略.

思路三: 利用位似比求坐標(biāo)比

點(diǎn)評(píng)位似法是解決與線(xiàn)段有關(guān)的幾何問(wèn)題的常用方法.利用三角形位似比設(shè)出點(diǎn)C的坐標(biāo)比,將點(diǎn)C代入直線(xiàn)AB中,可直接將直線(xiàn)AB的解析式轉(zhuǎn)化為二次函數(shù)的形式,最后利用二次函數(shù)的性質(zhì)即可求出最值.

思路四: 利用三角函數(shù)求解

解法8如圖10, 過(guò)點(diǎn)P向x軸作垂線(xiàn)PT,過(guò)點(diǎn)D向PT作垂線(xiàn)DT,二者交于T.軸, 所以∠TDA= ∠DAO,且∠PDB是定值. 所以∠PDT是定值, 在RtΔPRD中, sin ∠PDT也 是 定 值,

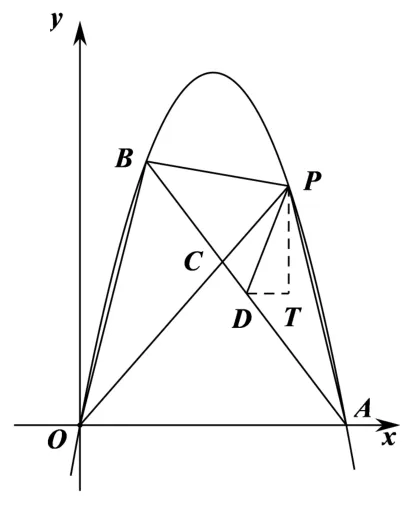
圖10

解法9同解法8, 在RtΔPRD中, cos ∠PDT是定

點(diǎn)評(píng)在RtΔPRD中借助“三角函數(shù)”由∠PDT的正余弦值推理得到線(xiàn)段PT或DT與線(xiàn)段PD間的長(zhǎng)度關(guān)系,最后利用點(diǎn)坐標(biāo)表示出線(xiàn)段的二次函數(shù)方程,求出的最大值.

4 解后反思

通過(guò)多視角的解題分析可以發(fā)現(xiàn),2022 年福建中考數(shù)學(xué)對(duì)二次函數(shù)綜合題的考查立意新穎,靈活多樣,不僅考查了學(xué)生對(duì)函數(shù)基本知識(shí)的掌握情況,還考查了他們的數(shù)學(xué)思維能力與數(shù)學(xué)學(xué)科核心素養(yǎng). 中考二次函數(shù)綜合題具有極高的靈活性和多樣性,沒(méi)有一種固定的解決方法[2]. 因此,在日常教學(xué)中,教師可以依托解題活動(dòng)訓(xùn)練學(xué)生數(shù)學(xué)思維,注重多視角分析綜合題,對(duì)綜合題進(jìn)行一題多解的思考與探究,幫助學(xué)生形成運(yùn)用數(shù)學(xué)思維方法尋找解題思路的習(xí)慣,培養(yǎng)從多個(gè)角度分析和解決問(wèn)題的能力.