橋梁樁基對碎石土邊坡動力響應的研究

1 引言

我國西南地區位于印度洋板塊與亞歐板塊之間， 地震斷裂帶十分活躍，是我國的一個地震高發區[1-2]。 同時西南地區位于青藏高原東側，地形陡峭險峻，地勢高低不平，山林河谷密布，高速公路、鐵路等線路工程為了滿足選線和保護生態的需求，跨越山區的橋梁樁基不可避免需建立在斜坡地段上。 斜坡上橋梁樁基兼具抗滑與承重兩方面特性， 并且在動力荷載作用時受力相比平地要更為復雜， 但斜坡上的樁基與其所在的邊坡是同一系統當中相互影響的兩部分， 邊坡的動力響應也在樁基的影響下發生變化，因此，研究樁基和邊坡相互作用下的動力響應具有重要的現實意義。

斜坡抗震穩定性及其加固一直以來是土木工程界重點關注的課題，早期人們主要從理論方面進行研究[3-4]。 葉海林等[5]針對傳統擬靜力法的不足， 基于強度折減分析法提出一種邊坡抗震設計新方法。 張劭華等[6]在靜力分析的基礎上，采用三維非線性有限元時程分析方法，考慮地基的輻射阻尼效應，對某巖質邊坡工程進行動力分析， 得出了邊坡在設計地震作用下的動力響應規律。 近來在軟件的快速發展下，學者們開展了各種數值模擬分析樁基與邊坡相互作用下的動力響應。 胡文杰[7]運用Midas GTS 對山區斜坡動力響應進行了分析，在劉晶波[8]的研究基礎上，通過計算表明地震作用下模型邊界采用一致黏彈性邊界能較好地處理，且能收到比較真實可靠的效果，樁基能夠對地震作用下的邊坡起一定的保護作用。

雖然目前的邊坡抗震理論以及分析方法越來越多，但是抗震研究多集中在邊坡中的樁基上， 對邊坡在樁基作用下的抗震研究較缺乏。 本文以有橋梁樁基存在的碎石土邊坡為背景，運用ABAQUS 進行三維有限元分析，探討橋梁樁基存在對邊坡動力響應的影響， 可為類似工況邊坡抗震提供參考。

2 工程概況及參數選擇

2.1 工程概況

計算所依托工程為西南地區某公路特大拱橋， 如圖1 所示。 工程場地所處地貌單元屬于構造侵蝕高中山峽谷地貌，其微地貌為峽谷地貌， 以擬建大橋右岸為主要研究對象， 右岸（東岸）為土質岸坡，地形坡度相對較緩，上部覆蓋較厚的崩坡積碎塊石土層，下伏奧陶系、志留系、寒武系巖層。

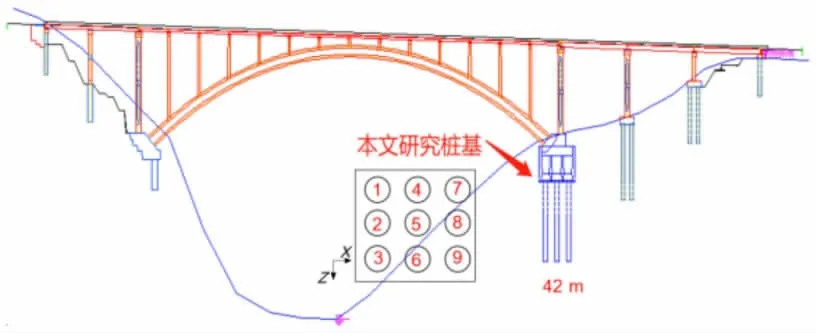
圖1 某拱橋斜坡樁基布置圖

2.2 地震波的選擇

依據JTG/T 2231-01—2020《公路橋梁抗震設計規范》，特征周期0.45 s，場地類別II 類，抗震設防烈度為7 度。地震波一要求般輸入地震動的持續時間不短于結構基本周期的5~10倍，且保證地震動的加速度最大值在所選范圍內[9]。 本文截取El-centro 波前30 s 作為地震動輸入，時間步長為0.02 s（見圖2）。 利用SeismoSignal 軟件通過對地震波進行基線校正和濾波處理從而避免模型出現漂移現象。

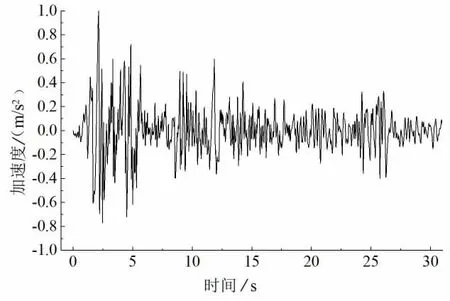
圖2 本場地使用的El-Cent r o 地震波

3 有限元模型

根據土層分布簡化為3 層， 從上至下分別為稍密碎石土層、中密碎石土層以及基巖，樁基建立在實際右岸邊坡中較平緩的位置，坡面為30°，建模過程邊坡與樁基均使用六面體實體單元，無樁基單元總數為39 772 個，有樁基單元總數41 418個，模型簡圖如圖3 所示。

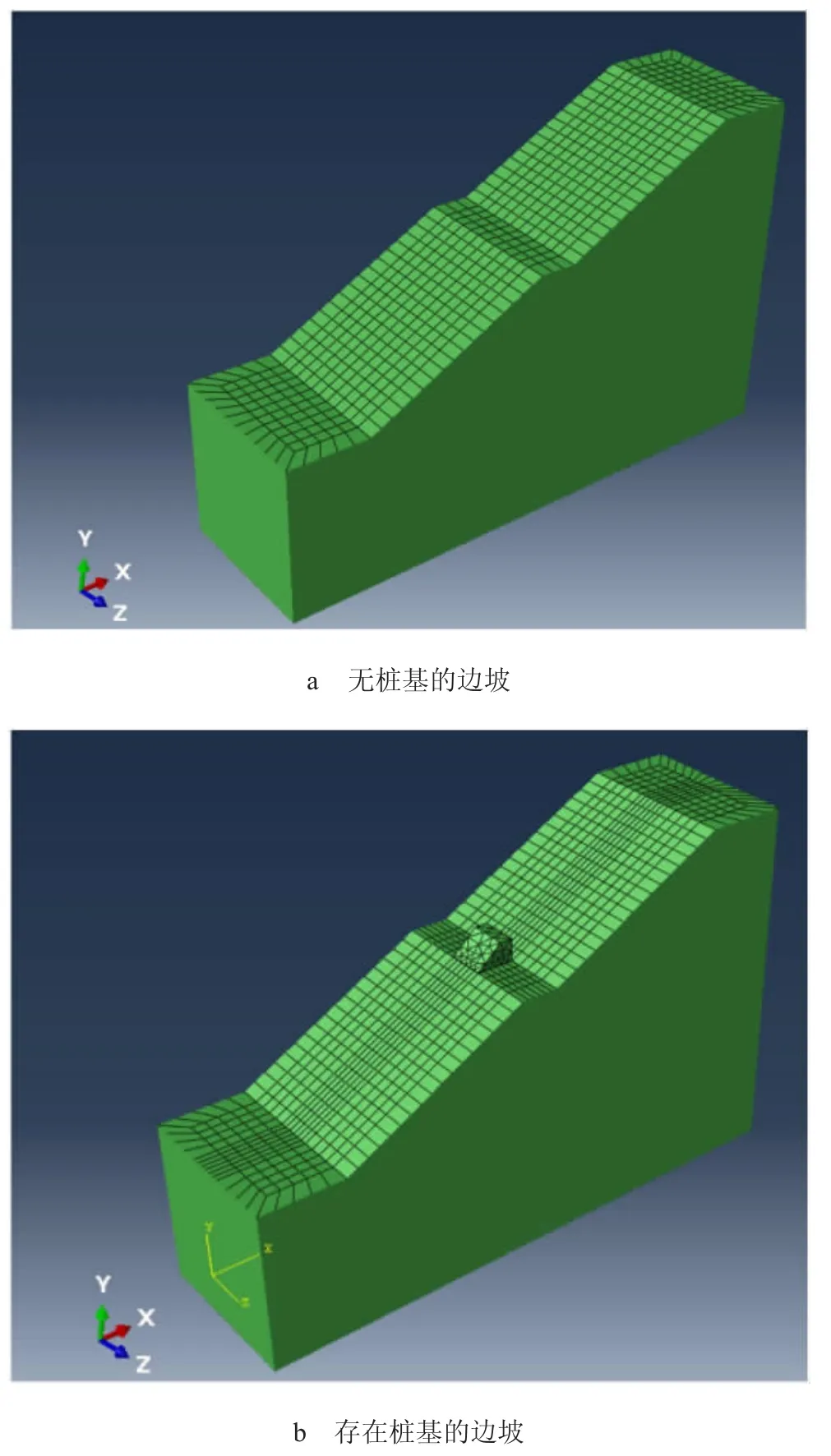
圖3 有限元邊坡模型

根據實際工程地質勘察以及鉆探， 模型材料參數取值如下表，承臺采用C40 混凝土彈性材料，樁基為C35 混凝土線彈性材料，材料參數設置如表1 所示。

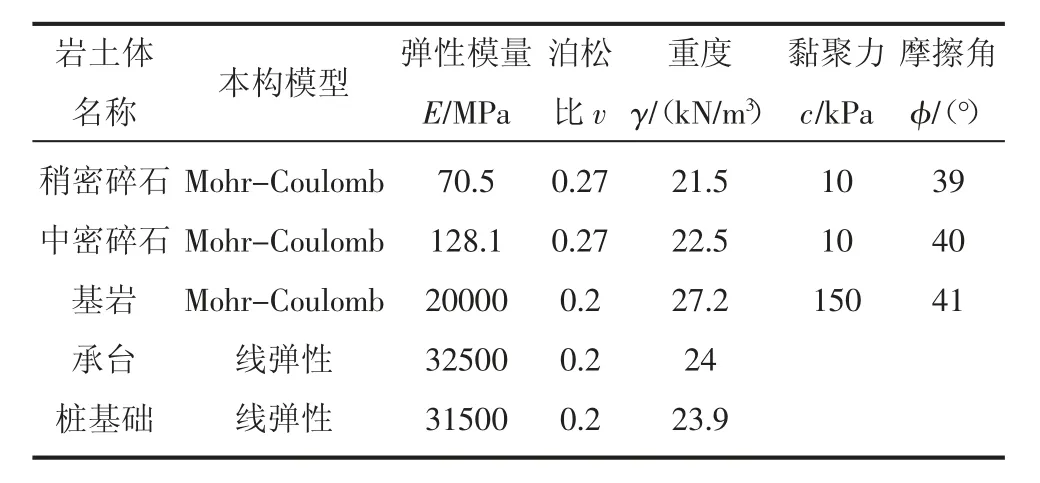
表1 單樁數值模擬參數

4 地震作用下邊坡動力響應分析

4.1 有無樁基邊坡塑性應變研究

圖4 展示了兩種三維有限元模型分別在0.1g、0.2g 和0.4g 地震動作用下的有效塑性區云圖切片，可以明顯看出：隨著地震動峰值的不斷增大，邊坡塑性區域的面積也隨之擴大；塑性區域主要集中在邊坡上層碎石土中， 坡頂及邊坡上半部分塑性區開展明顯，展現出碎石土的非線性特征。 無樁基的情況下， 邊坡上下部分塑性區有連通的趨勢， 有群樁存在的邊坡， 隨著地震動作用的變化在群樁處塑性區有不同程度的縮小，碎石土中沒有出現塑性貫通的現象。 可見邊坡上的橋梁樁基礎不僅有承受上部結構荷載的功能，還兼具穩固邊坡，減小塑性區的作用。

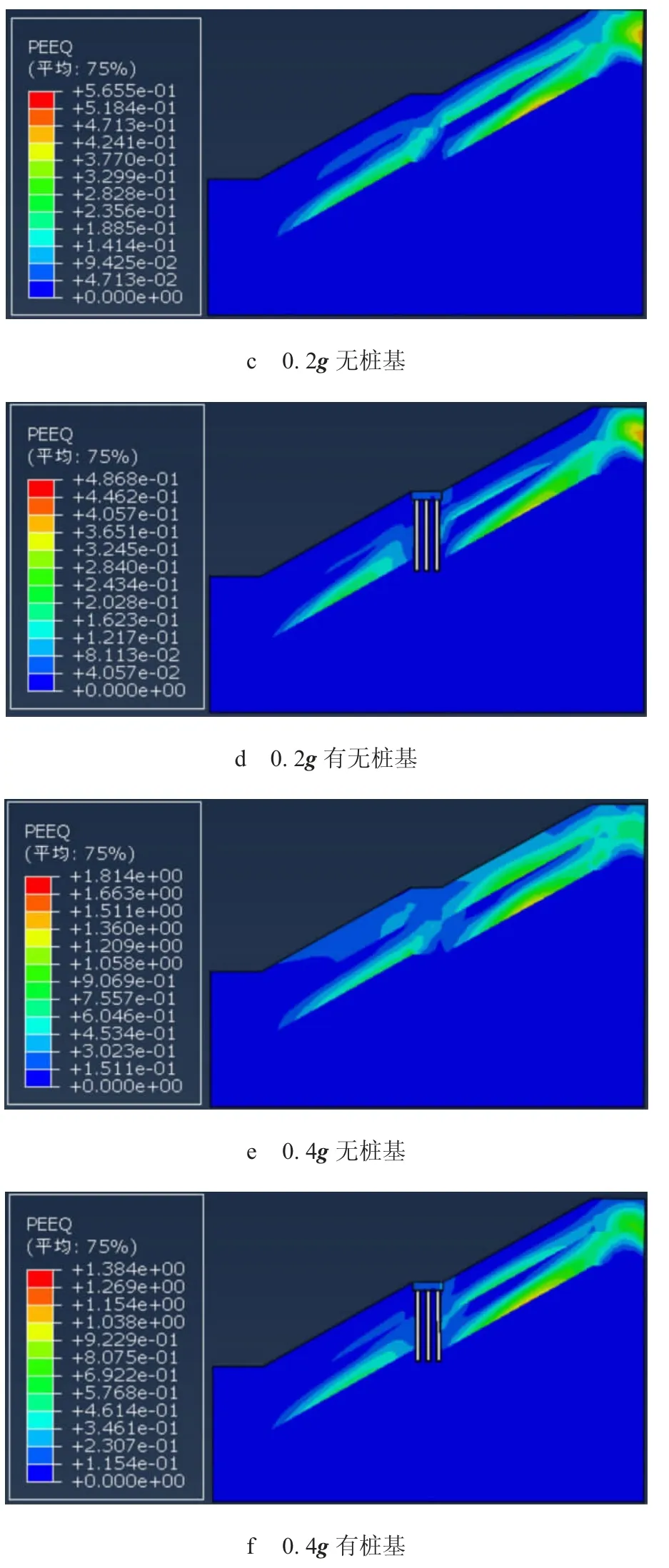
圖4 動力作用下有無樁基的邊坡塑性區（PEEQ 為等效塑性應變）

4.2 有無樁基的邊坡安全系數

邊坡安全系數能夠從整體上反映出邊坡的穩定狀態，代表了土體強度經過一定系數的折減后能達到極限平衡狀態。采用有限元強度折減法對邊坡安全性進行驗算。 強度折減法的計算公式為：

式中，c、φ 為強度折減前土體的黏聚力與內摩擦角；c＇、φ＇為強度折減后土體的黏聚力與內摩擦角；F 為邊坡的安全系數。

有無樁基的邊坡在不同峰值地震動作用下按強度折減法得到的邊坡安全系數如圖5 所示。 結果表明：邊坡上存在樁基后邊坡的安全系數得到了顯著提升， 地震動加速度峰值0.1g時安全系數提高0.15， 地震動加速度峰值0.2g 時安全系數提高0.1、 地震動加速度峰值0.3~0.4g 時安全系數提高約0.05；無樁基時邊坡在0.2g 地震動及以上地震荷載作用時均未達到規范所規定的1.15 的安全值[10]，而邊坡在有樁基的情況下除了在0.4g 地震作用時，其余安全系數均能達到1.15。說明樁基的存在能有效增加邊坡的穩定性。

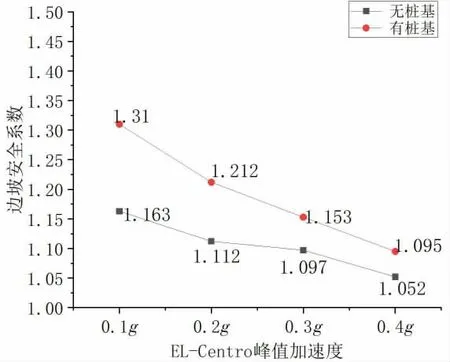
圖5 不同地震動邊坡安全系數

4.3 有無樁基的邊坡加速度響應

在坡面從下往上按5 等分布置5 個測點A~E，E 點為坡腳（見圖6），定義相對高程為0，則D、C、B、A 相對高程分別為0.25、0.5、0.75、1。 在各測點監測坡體的加速度、位移等數據。

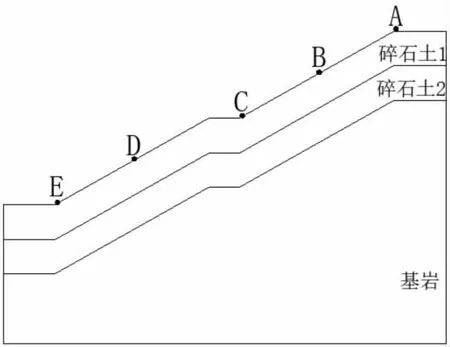
圖6 坡面監測點示意

限于篇幅， 僅展示加速度峰值0.1g 地震動作用下有無樁基的邊坡基巖與C 監測點的加速度時程曲線，如圖7 所示。監測點的加速度時程與基巖處的加速度時程形狀相似， 但其圖形在整體上要比基巖處的加速度時程向右偏移， 即邊坡坡面點的加速度時程存在滯后現象。 這是由于地震波在土體、樁基中的傳播時間、土層應變、樁與土相互作用等因素帶來的滯后效應。 各監測點在持時為30 s 的El-Centro 地震動作用下，加速度峰值放大系數K 可用式（3）表示：

圖7 有無樁基的加速度響應時程

式中，Amax為動力響應加速度峰值；A 為對應的基巖在該時段內的動力響應加速度峰值。

在圖8a 中展示了有無樁基的兩種邊坡在0.1g 地震動作用下加速度放大系數K 與邊坡高程之間的關系。相對高程0.5處為樁基位置， 在此處兩種邊坡模型加速度放大系數相差較大，有樁基時加速度放大系數為1.91，相對無樁基時加速度放大系數2.42 減小了21.1%， 這說明樁基礎對周邊土體存在約束作用，而其余測點加速度放大系數相差不大，表明樁基對土體有約束作用，但范圍有限。 隨著高程的增加，加速度放大效果越明顯， 均在最高點處加速度放大系數達到最大值； 圖8b展示了兩種工況下C 監測點在不同地震動作用下樁基處放大系數的變化趨勢， 可以看出兩種工況下加速度放大系數都隨峰值加速度的增大而減小，且減小趨勢相同，同時樁基工況下加速度放大系數均小于無樁基工況。 在0.1g~0.4g 峰值加速度地震作用下，樁基工況下加速度放大系數分別下降了21.1%、26.5%、31.8%、34.1%，以上說明了樁基能夠起到增加地震作用下邊坡的穩定性的作用。

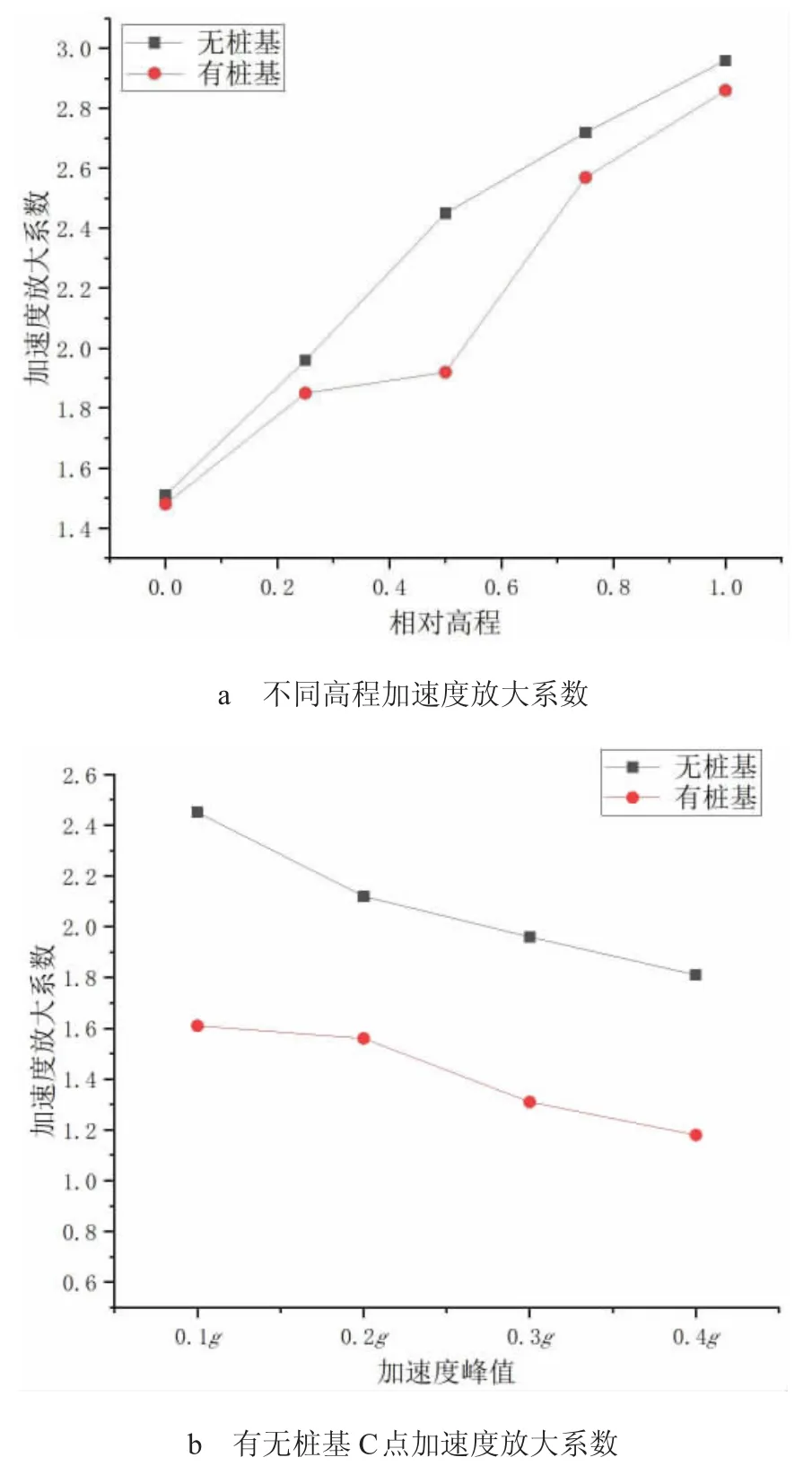
圖8 邊坡表面加速度放大系數

5 結論

本文通過ABAQUS 有限元軟件對典型邊坡進行三維建模，對比了有無樁基的邊坡塑性區和加速度等動力響應參數。

1）有限元計算結果表明樁基的存在，不僅可以承載上部結構的荷載，還可以減小邊坡在動力作用下的塑性應變。