一個新的逆向Hilbert型不等式

劉 瑤，席高文（重慶科技學院 數理學院，重慶 401331）

一個新的逆向Hilbert型不等式

劉 瑤，席高文（重慶科技學院 數理學院，重慶 401331）

Hilbert不等式倍受數學家的關注，并得到廣泛應用。通過建立權系數不等式，得到一個新的逆向Hilbert型不等式，并證明其常數因子為最佳值，同時還考慮其等價形式。

Hilbert型不等式；權系數；等價式；最佳常數因子

0 引 言

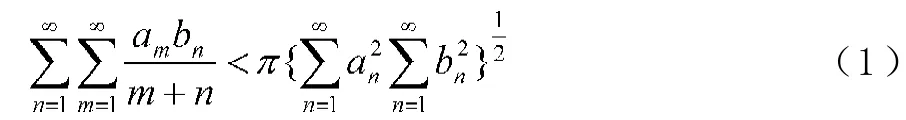
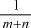
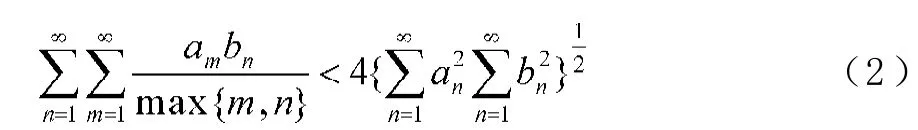
這里，常數因子4為最佳值。

Hilbert型不等式是核為雙線型且齊次的以Hilbert不等式為代表的一類不等式，它們在分析學中有重要的應用［1-3］。1991年我國知名數學家徐利治教授首倡了旨在加強Hilbert不等式的權系數方法，楊必成［4-5］對它們作了推廣，并在文獻［6-7］中運用權系數方法，建立了如下具有混合核的逆向Hilbert型不等式：

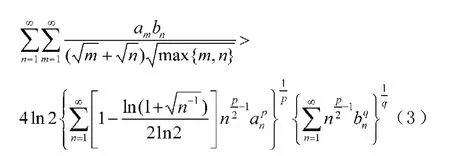
這里，常數因子4ln2為最佳值。

王愛珍等［8］引入單參量λ及估算權系數，建立了（3）式的如下最佳推廣形式：

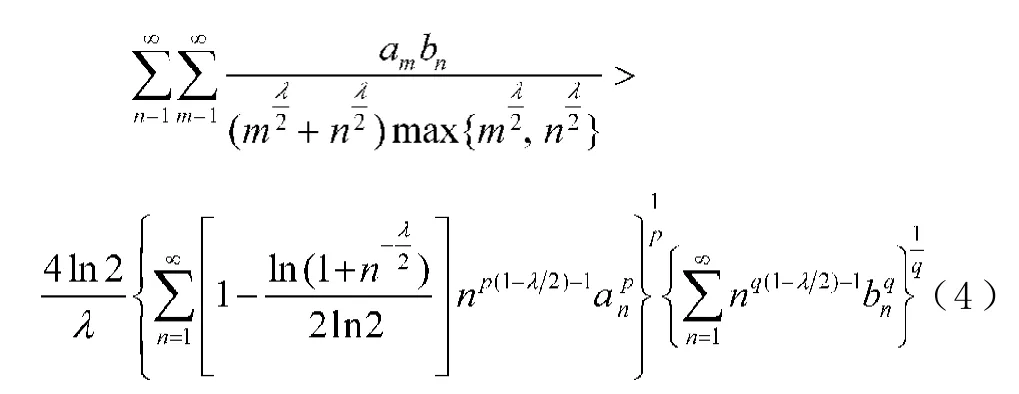
本文通過建立權系數不等式，得到一個新的具有混合核的逆向Hilbert型不等式，同時還考慮其等價形式。

1 兩個引理

引理1 定義權系數為：

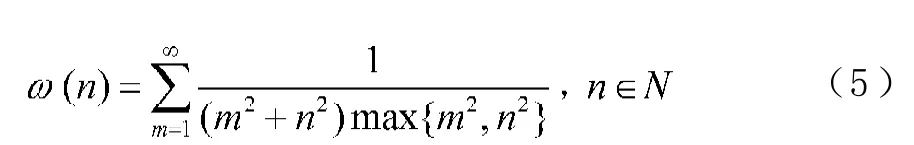
則有

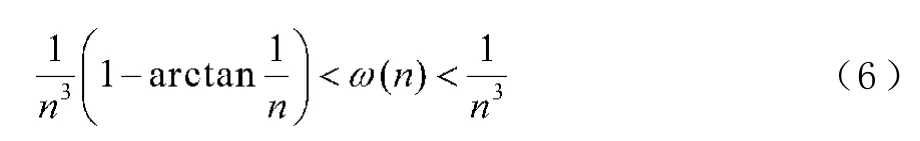
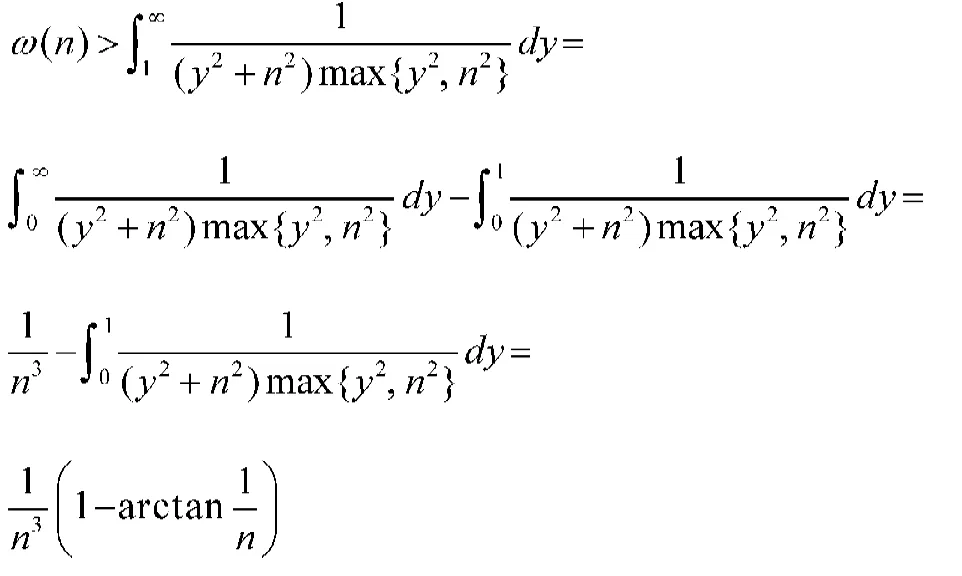
故（4）式成立。證畢。

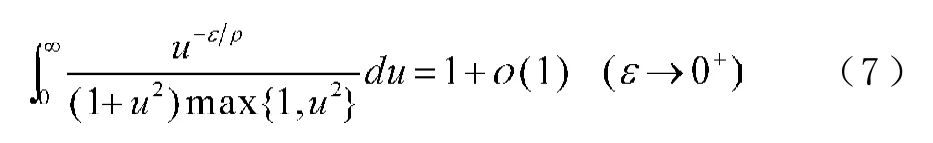
故（7）式成立。證畢。

2 主要結果

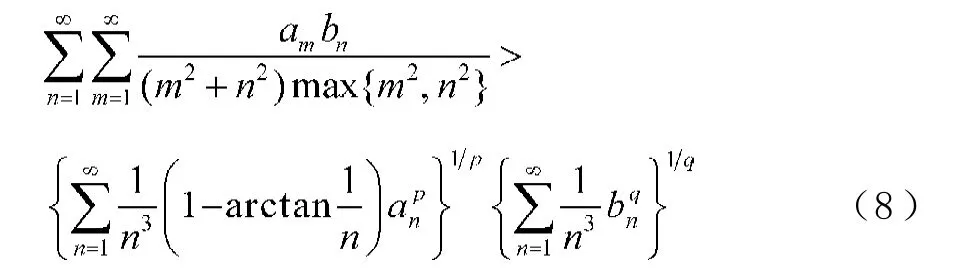
這里，常數因子1為最佳值。

證明 由帶權的反向的H? lder不等式及（5）式，有

再由（4）式，其中q＜0，有（6）式。

以下證明（8）式的常數因子1為最佳值。

若（8）式的常數因子1不是最佳值，則存在k＞1，使得（8）式成為

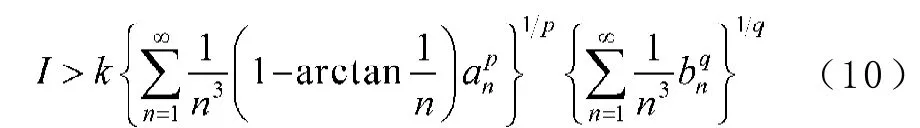
對任意的ε∈（0， p），在（10）式中，取an=n-ε/p，bn=n-ε/q，n∈N，代入（10）式，則有

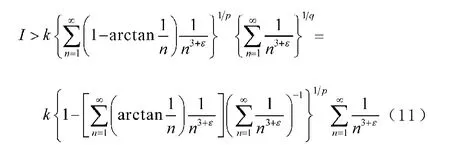
將上述an，bn代入（8）式的左邊并運用（7）式，則有

從而由（11）式和（12）式，有

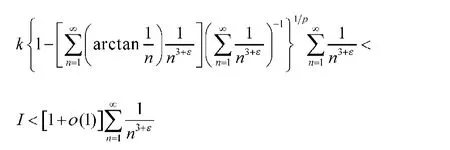
取極限，有 與前面的假設矛盾，故（6）式的常數因子1為最佳值。證畢。

3 等價形式

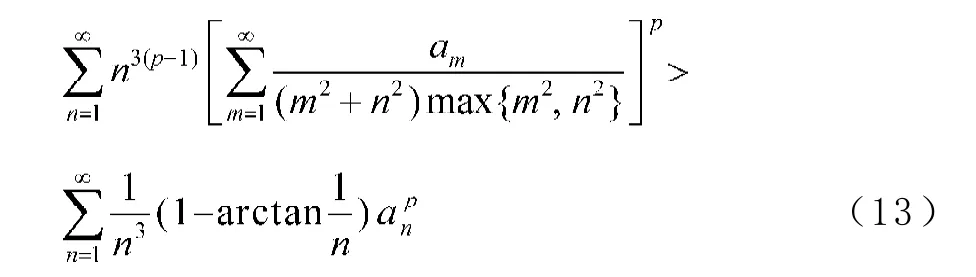
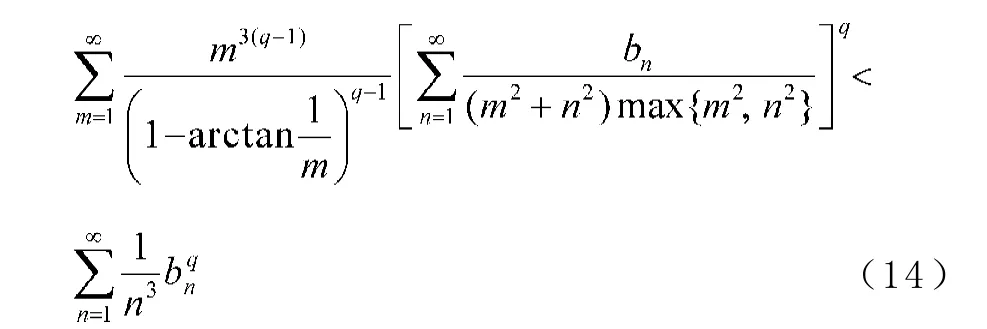
這里，（13）式和（14）式的常數因子1都為最佳值，且（13）式和（14）式均與（8）式等價。

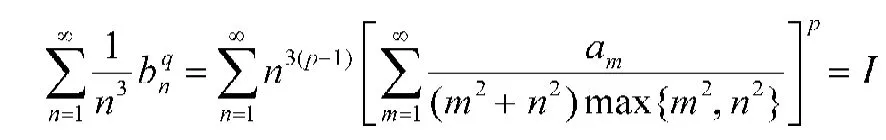
當I=∞，（13）式成立；設0＜I＜∞，則由（8）式有

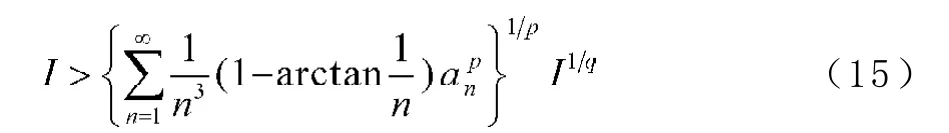
在（15）式的兩邊同除I1/q，然后p次方，有

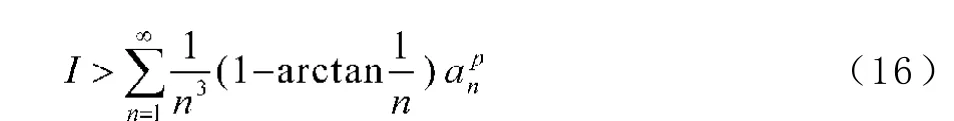
故（13）式成立。

反之，若（13）式成立，配方，由反向的H?lder不等式，有

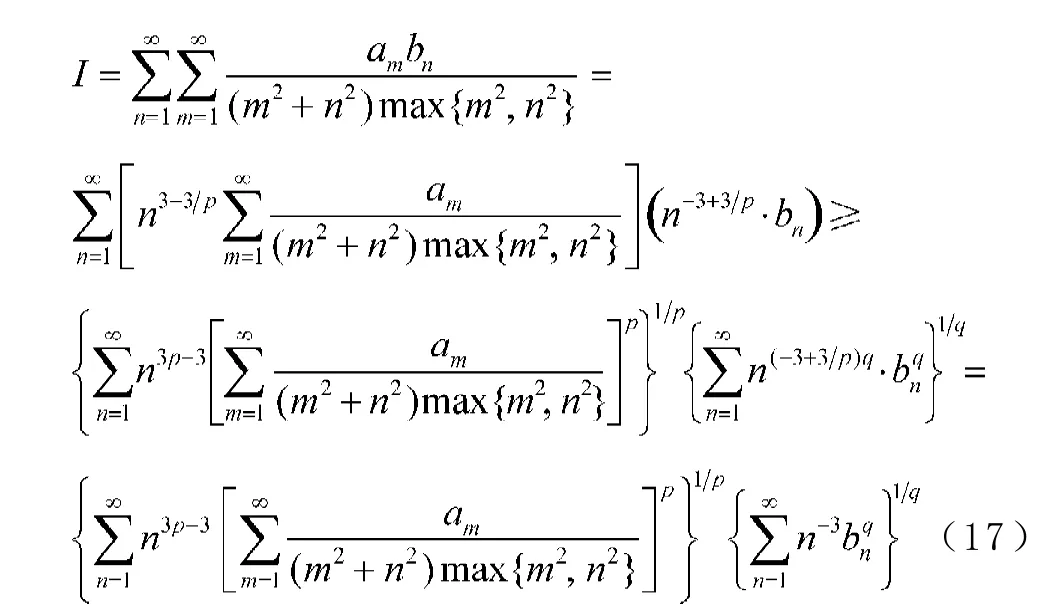
由（13）式，則有

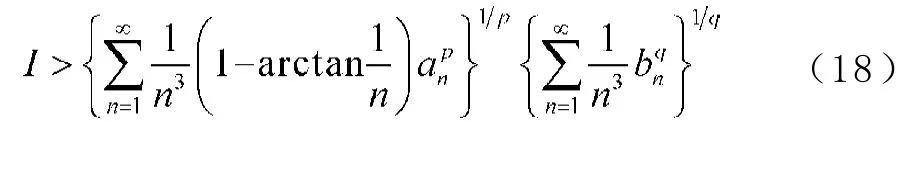
故（13）式與（8）式是等價的。若（13）式的常數因子不是最佳值，則由（17）式，易得（8）式的常數因子亦不是最佳值，存在矛盾。

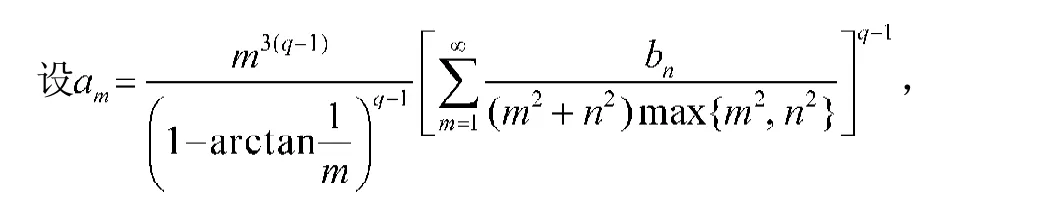
則由（9）式，其中q＜0，有

反之，若（14）式成立，配方，由反向的H?lder不等式，有

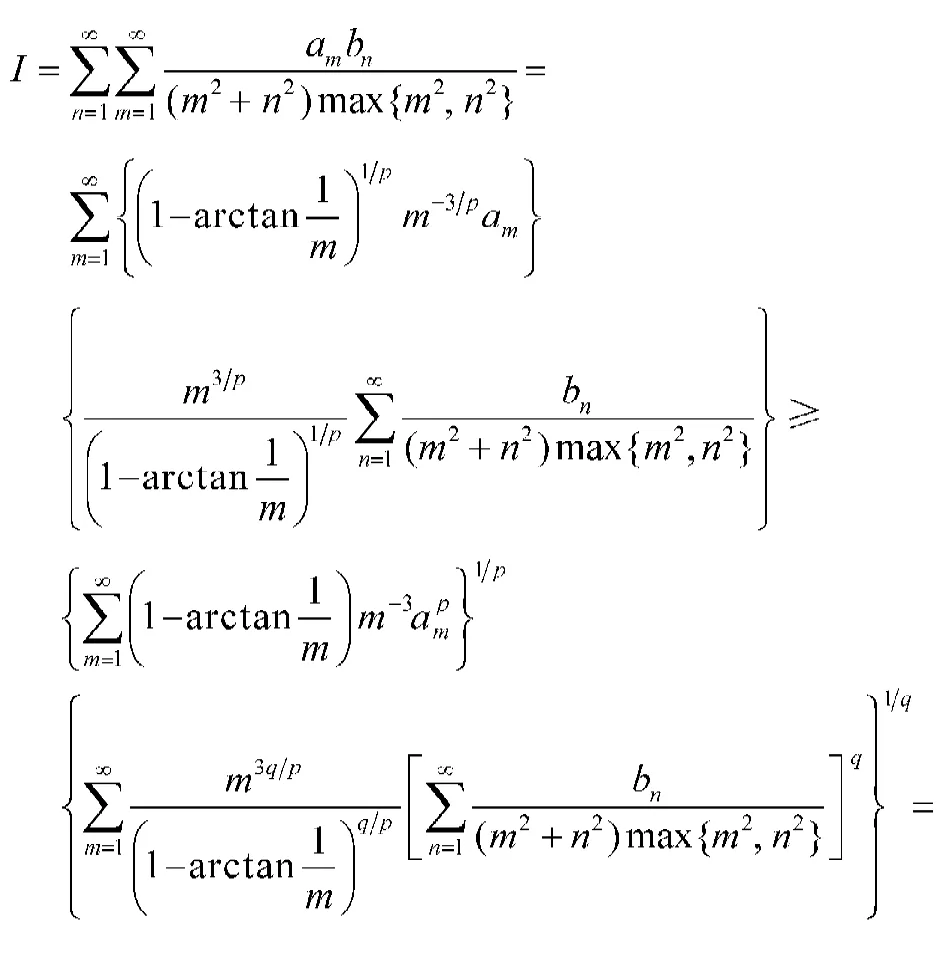
再由（14）式，其中q＜0，有（8）式。故（14）式與（8）式是等價的。同理可證明（14）式的常數因子為最佳值。

評注 顯然，逆向Hilbert型不等式：

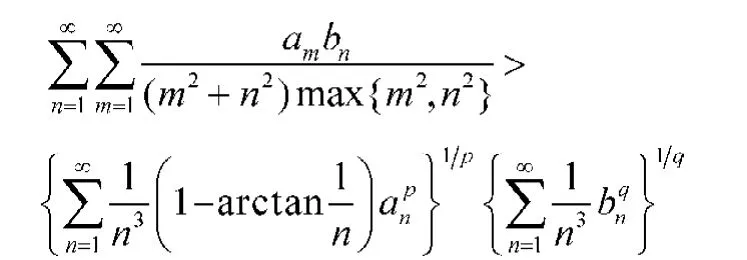
它是一個新的具有混合核的不等式，且常數因子1為最佳值。此不等式也是對（4）式的一個推廣，（13）式和（1 4）式是它的等價形式。

［1］HARDY G H，LITTLEWOOD J E，POLYA G.Inequalities［M］.Cambridge:Cambridge University Press，1934.

［2］MINTRINOVIC D S，PECARIC J E，FINK A M.Inequalities Involving Functions and Their Integrals and Derivatives［M］.Boston:Kluwer Academic Publishers，1991:181-215.

［3］匡繼昌.常用不等式［M］.濟南:山東科學技術出版社，2004.

［4］YANG B C.On an Extended of Hardy-Hilbert’s Inequality［J］.Chinese Annals of Mathmatics，23A（2）:247-254.

［5］YANG B C.On an Extended Hardy-Hilbert’s Inequality and Some Reversed Form［J］.International Mathematical Forum，39（1）: 1905-1912.

［6］楊必成.一個新的Hilbert型不等式［J］.上海大學學報（自然科學版），2007，13（3）:274-278.

［7］YANG B C，RASSIAS T M.On the Way of Weight Coefficient and Research for the Hilbert-type Inequalities［J］.Mathematical Inequalities and Applications，2003，6（4）:625-658.

［8］王愛珍，楊必成.一個逆向Hilbert型不等式的最佳推廣［J］.武漢大學學報（理學版），2008，54（3）:275-278.

［責任編輯：王瑋明］

A New Reverse Hilbert Inequality

LIU Yao， XI Gaowen （College of Mathematics and Physics， Chongqing University of Science & Technology， Chongqing， 401331， China）

Hilbert inequality has drawn a lot of attention from mathematicians and is widely used.Weight coefficient inequality is set up， which leads to a new reverse Hilbert inequality， and also proves its constant factor is the optimal values.Meanwhile， its equivalent form is considered.

Hilbert inequality； Weight coefficient； Equivalent form； Optimal constant factor

10.13669/j.cnki.33-1276/z.2016.039

O178

A

1671-4326（2016）03-0068-05

2016-01-25

劉 瑤（1992—），女，重慶梁平人，重慶科技學院數理學院本科生；

席高文（1963—），男，河南靈寶人，重慶科技學院數理學院教授.