三維延拓Kantorovich法的迭代不收斂現象
林永靜(溫州職業技術學院 建筑工程系,浙江 溫州 325035)
三維延拓Kantorovich法的迭代不收斂現象
林永靜(溫州職業技術學院 建筑工程系,浙江 溫州 325035)
將二維延拓Kantorovich法推廣到三維延拓Kantorovich法時,通過大量數值算例發現了一個新現象,即如果采用簡單形式的三維延拓Kantorovich法,那么會遇到迭代不收斂的數值困難。對此數值現象進行定性分析,可得出結論:三維延拓Kantorovich法并不是二維延拓Kantorovich法的簡單推廣,二者有著本質的不同。
三維延拓Kantorovich法;簡單形式;迭代不收斂
0 引 言
在已有研究[1-4]的數值算例中,二維延拓Kantorovich法表現出顯著的計算優越性,既有很高的計算精度,又有很高的計算效率。一元函數乘積和的函數逼近形式帶來很高的逼近精度,往往2~3項就有足夠的精度。對兩個維度“分而治之”的迭代策略大大減少了計算量,帶來很高的計算效率。
考慮到延拓Kantorovich法具有高精度、高效率的特點,尤其是“分而治之”的迭代策略在三維問題中可能有高效率的表現,因而將二維延拓Kantorovich法推廣到三維延拓Kantorovich法。原本預計該項新研究屬于推廣性研究,后來發現這低估了研究的意義和難度。通過大量數值算例發現了一個新現象,即如果采用簡單形式的三維延拓Kantorovich法,會遇到迭代不收斂的數值困難。
1 模型方程
以三維立方體域上的Poisson方程為例,三維Poisson方程對應的能量泛函為:
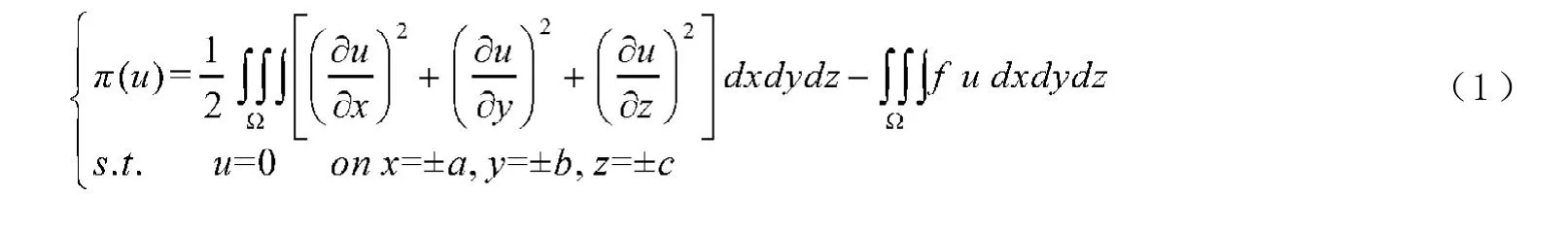
其中Ω為規則區域[-a, a]×[-b, b]×[-c, c]。
仿照二維延拓Kantorovich法,取試探函數構造形式為:
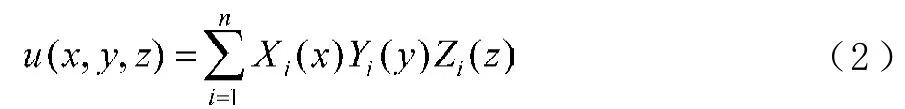
這種簡單的函數構造形式在三個維度上是對稱的。
2 算法實施
2.1 積分微分方程組
將(2)式代入(1)式,通過取變分,可得到一套耦合的積分微分方程組為:
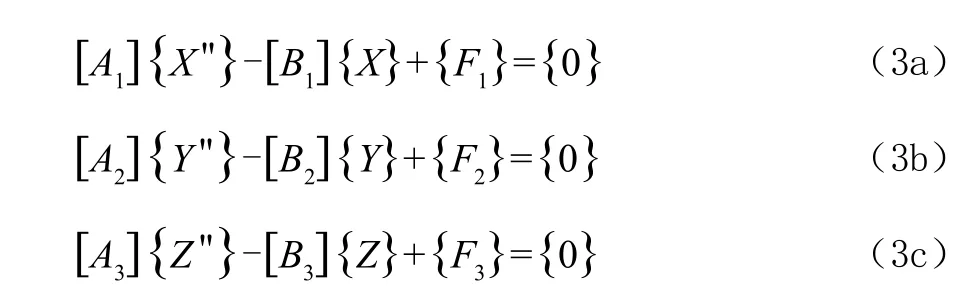
邊界條件為:
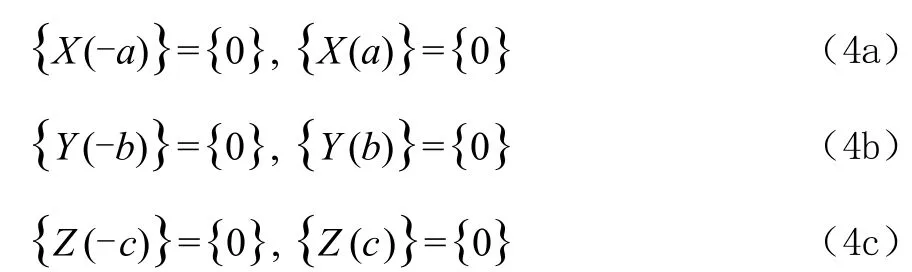
其中的各項系數為:

2.2 迭代步驟
因為在(2)式的函數逼近式中,三個維度輪換對稱,所以算法的迭代過程將按三個維度輪換迭代求解。一個循環過程由(a)→(b)→(c)共三步組成(不失一般性地,假定在第一步(a)中已知{X}、{Y}而去求{Z}):
(a)固定{X}、{Y},則積分微分方程組簡化為常微分方程組(3c)、(4c),求解常微分方程組(3c)、(4c)得{Z};
(b)固定{Y}、{Z},則積分微分方程組簡化為常微分方程組(3a)、(4a),求解常微分方程組(3a)、(4a)得{X};
(c)固定{X}、{Z},則積分微分方程組簡化為常微分方程組(3b)、(4b),求解常微分方程組(3b)、(4b)得{Y}。
至此已完成了一個循環過程,檢驗數值解的誤差是否已小于誤差限,若是則結束迭代,否則返回(a)進入新一輪的循環。
3 數值算例
數值算例中的常微分方程組采用常微分方程求解器COLSYS[5-6]來求解。
算例 三維Poisson方程。
設定邊界條件為:u=0, on x=±a, y=±b, z=±c,給定數據為:a=b=c=1,f=2,如圖1所示。取初始試探函數為:
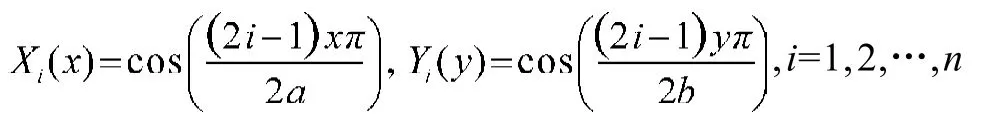
計算結果由圖2~圖3給出。需要說明的是,輪數與次數不同,輪數是指大的循環過程的個數,而次數是指小的迭代步驟的個數。對于簡單形式,每一輪循環里包含三次迭代。
3.1 取兩項試探函數
(1)前20輪循環的中心點位移。由圖2可知,在前10輪循環內,迭代比較快地趨向于一個數值。但需要注意的是,迭代過程并不收斂,由局部放大圖可看出,后1 0輪循環的變化比較均勻,并不趨于收斂。
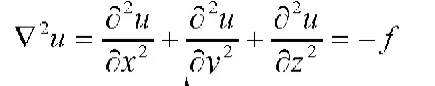
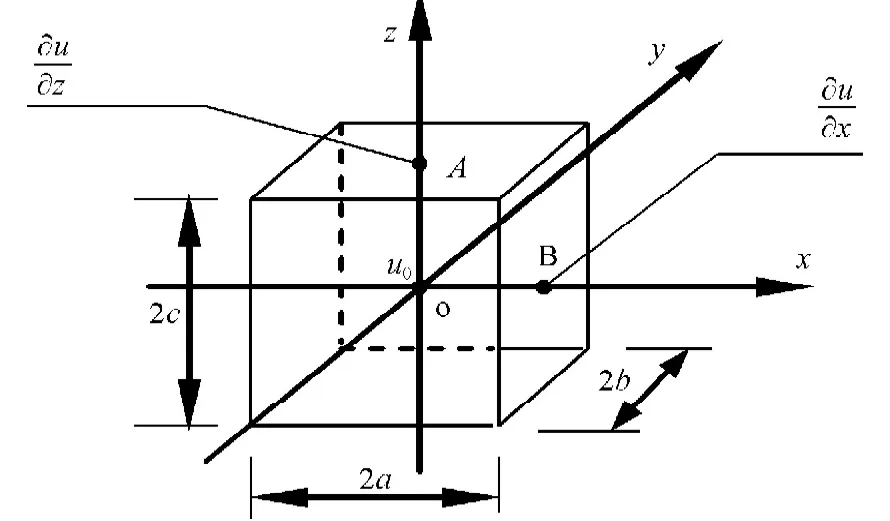
圖1 三維Poisson方程
(2)前1 000輪循環的后10輪循環的中心點位移。由圖3可知,在后10輪循環內,迭代變化均勻。均勻的迭代變化趨勢顯示,這個迭代過程并不收斂。
3.2 取三項試探函數
限于篇幅,這里不再列出具體數據。取三項試探函數與取兩項試探函數相比,其迭代變化情況相似,后
10 輪循環的迭代變化也均勻,迭代過程也并不收斂。
以上數值試驗表明,簡單形式的三維延拓Kantorovich法,當取多項時將遇到迭代不收斂的數值困難。盡管開始階段能較快地(在10輪循環內)趨于某個固定值,但迭代過程仍不收斂,后面的迭代過程都在均勻地變化,沒有收斂的趨勢。
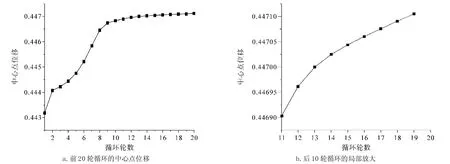
圖2 前20輪循環的中心點位移及其后10輪的局部放大
4 定性分析
4.1 與二維延拓Kantorovich法的比較
與二維延拓Kantorovich法相比,三維延拓Kantorovich法的迭代收斂更困難,其簡單形式甚至迭代不收斂。
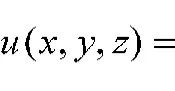
(2)迭代效率。二維延拓Kantorovich法的迭代收斂非常迅速,一般只需2~3次迭代。簡單形式的三維延拓Kantorovich法遇到了迭代不收斂的數值困難。
4.2 迭代不收斂的原因
在三維延拓Kantorovich法中,迭代不收斂的原因,可從最小計算代價的角度給出一個定性討論。
對于簡單形式的三維延拓Kantorovich法,多項試探函數的逼近精度較高,相應地需要較高的計算代價,而每個維度的計算量卻都很小,從而導致這種高逼近精度無法通過單個維度的計算量的累加達到。可見,迭代不收斂似乎與計算代價過少有關。
從這個角度看,三維延拓Kantorovich法要想實現迭代收斂,則不能過度地節省計算量,需要考慮增加更多的計算量。文獻[7-8]證實了這個觀點:采用張量積的函數構造形式,其中一個方向上有n2個函數變量,比起簡單形式在每個方向上只有n個函數變量,函數變量的個數大大增加,相應的計算量大大增加,結果實現了迭代收斂。張量積形式的中心點位移大約經過3輪循環趨于收斂,其迭代計算結果見表1。

表1 張量積形式的中心點位移的迭代計算結果
5 結束語
根據以上數值算例和定性分析,可得出關于三維延拓Kantorovich法的以下結論:
(1)采用簡單形式的三維延拓Kantorovich法會遇到數值困難。當取多項試探函數時,函數值迭代不收斂,泛函值的單調下降也極其緩慢;當循環輪數非常高時,這種均勻變化的不收斂趨勢更加明顯。
(2)數值困難顯示,三維延拓Kantorovich法與二維延拓Kantorovich法有著本質的不同。
[1]KANTOROVICH L V,KRYLOV V L.Approximate Methods of Higher Analysis[M].New York:Interscience,1958.
[2]KERR D.An Extension of the Kantorovich Method[J].Quarterly of Applied Mathematics,1968(26):219-229.
[3]KERR A D,ALEXANDER H.An Application of the Extended Kantorovich Method to the Stress Analysis of a Clamped Rectangular Plate[J].Acta Mechanica,1968(2/3):180-196.
[4]WEBBER J P H.On the Extension of the Kantorovich Method[J].The Aeronautical Journal,1970,74:146-149.
[5]ASCHER U,CHRISTIANSEN J,RUSSELL R D.Collocation Software for Boundary-Value ODEs[J].ACM Transactions on Mathematical Software,1981(2):209-222.
[6]袁駟.介紹一個常微分方程邊值問題求解通用程序—COLSYS[J].計算結構力學及其應用,1990(2):104-105.
[7]林永靜,袁駟.張量積形式的三維延拓Kantorovich法[J].工程力學,2012(5):8-12.
[8]林永靜.張量積形式的三維延拓Kantorovich法求解彈性動力學問題[J].現代工業經濟和信息化,2016(6):110-112.
[責任編輯:武云鵬]
Iteration Non-Convergence Phenomenon of Three-Dimensional Extended Kantorovich Method
LIN Yongjing (Architecture Engineering Department, Wenzhou Vocational & Technical College, Wenzhou, 325035, China)
When two-dimensional extended Kantorovich method is introduced to three-dimensional extended Kantorovich method, a large number of numerical examples reveals a new phenomenon: if the simple three-dimensional extended Kantorovich method is used, the numerical difficulty of iteration non-convergence will occur.Qualitative analysis on this numerical phenomenon indicates that three-dimensional extended Kantorovich method is not a simple introduction of two-dimensional extended Kantorovich method, and they are different in nature.
Three-dimensional extended Kantorovich method; Simple form; Iteration non-convergence
10.13669/j.cnki.33-1276/z.2016.060
TU318;O343.2
A
1671-4326(2016)03-0047-04
2016-06-08
浙江省教育廳一般科研項目(Y201225911);溫州市科技計劃項目(S20110002)
林永靜(1975—),男,浙江樂清人,溫州職業技術學院建筑工程系講師,博士.

