多孔LiOH孔隙特征及CO2流動特性數值模擬

陳元超, 楊 俠, 曹吉胤, 劉 迎, 汪龍飛

(武漢工程大學 機電工程學院, 湖北 武漢 430205)

1 概述

LiOH是一種應用廣泛的二氧化碳吸附劑,通常通過添加造孔劑、干燥等手段,得到比表面積很高的多孔顆粒[1-2]。然而,多孔顆粒內部孔隙結構復雜、尺度變化較大,受技術條件的限制,對孔隙結構的相關研究,研究者大多采用簡單的幾何拓撲模型,已有豐富的成果[3-4]。

前人研究發現,固體吸附劑的幾何結構具有明顯的分形特征[5],陳林等人[6]研究發現分形理論可以很好地應用于定量分析顆粒的孔隙結構。劉俊亮等人[7]根據分形幾何理論的基本概念,利用Sierpinski結構對多孔介質微結構、孔隙率等參數給予詳細論述,并分析不同模型的滲透率與分形維數的關系與差異。孟祥奎[8]基于規則分形結構——Sierpinski地毯結構建立二維分形孔隙模型,模擬CaO孔隙流動規律,結果表明,氣體在Sierpinski地毯結構中流動具有分形特性、對稱性、隨機性。鄭瑛等人[9]利用Menger海綿構造了CaO孔隙結構,討論了Menger海綿孔隙率和比表面積隨分形維數的變化規律,分析了CaO孔隙結構對確定Menger海綿參數的要求。

本文基于規則分形結構——Sierpinski-Menger海綿結構建立三維分形孔隙模型,利用Fluent軟件,對LiOH孔隙氣體流動進行數值模擬,研究不同流動速度的流動規律及其對吸附效果的影響,為研究LiOH吸附劑吸附性能提供參考依據。

2 孔隙流動特性數值模擬

2.1 數學模型及方法

本文以二氧化碳氣體為流動介質,流動模型為三維可壓縮流體湍流流動,不考慮流動熱傳遞,流體流動過程遵循連續性方程、動量方程[10]。用非穩態隱式進行模擬求解,采用k-ε湍流模型,整體以SIMPLE二階迎風離散方法進行計算[11],多相模型采用Eulerian兩相模型。

2.2 Sierpinski-Menger海綿分形模型建立

Menger海綿分形在描述多孔介質方面有著廣泛的應用,是一種典型的自相似多孔介質分形技術。其構造方法是將立方體的邊(邊長為R)進行m等分,可得到m3個小立方體,邊長為R/m,然后隨機去掉其中n個立方體,剩下m3-n個立方體。如此進行下去,經過i次構造后,得到(m3-n)i個小立方體。經i次構造后得到的模型稱為i級模型。分形維數D的計算式為[12-13]:

(1)

式中D——分形維數

m——每次邊長等分的數量

n——每次隨機去掉的立方體的數量

當m為3,n為7時,D為2.726 8。該模型則是Sierpinski-Menger海綿分形模型[14]。模型孔隙率Φ的計算公式如下[15]:

Φ=1-(3D-3)i

(2)

式中Φ——模型孔隙率

i——構造次數

2級模型、3級模型孔隙率分別為0.45、0.59。

2.3 幾何模型建立及網格劃分

在SolidWorks中建立2級、3級Sierpinski-Menger海綿分型模型(簡稱2級模型、3級模型),其尺寸為0.27 mm×0.27 mm×0.27 mm,2級模型見圖1a,3級模型見圖1b。選用六面體網格,單元尺寸為0.005 mm,2級模型網格見圖1c,網格數量為86 400,3級模型網格見圖1d,網格數量為64 000。

2.4 邊界條件

設置y=0截面為入口,y=0.27 mm截面為出口,其他面設置為壁面邊界。入口邊界條件為速度入口,速度為0.01、0.1、1 mm/s;出口邊界為壓力出口,出口壓力為默認值0。環境溫度為室溫293.15 K,大氣壓力為101.325 kPa,流體為空氣與二氧化碳。主要考慮內部孔隙結構對流體流動的影響,為了方便研究分析,模型流道內部初始充滿空氣(二氧化碳的體積分數約為0.04%),入口流體二氧化碳質量分數為1。

3 結果及分析

3.1 不同級數模型流動特性分析

入口氣體流速為0.1 mm/s、流動時間為20 s時,2級、3級模型中z=0.205 mm截面CO2速率與動壓云圖見圖2。可以分析得出,同一級數下速率與動壓分布基本一致,有明顯的分形特性;不同級數模型的CO2速率與動壓分布均具有相似性及對稱性,這是由海綿模型本身特性所決定,盡管模型的級數不同,但它們的分形維數相同,在同一分形維數下,不同級數的模型也具有相同的分形特征。

3.2 3種入口氣體流速下2級模型CO2體積分數分布

2級模型z=0.205 mm截面不同入口氣體流速、不同時刻二氧化碳體積分數分布見圖3。通過比較不同入口氣體流速下二氧化碳體積分數分布情況,可以看到二氧化碳體積分數在固體域后方分布很少,形成反應死區,入口氣體流速越大反應死區面積越小。這種情況說明,入口氣體流速的增大,有利于二氧化碳分布均勻,在允許的范圍內增加入口氣體流速有利于二氧化碳的吸附,提高LiOH吸附劑的吸附率。

圖3 2級模型z=0.205 mm截面不同入口氣體流速、不同時刻CO2體積分數分布(軟件截圖)

3.3 3種入口氣體流速下3級模型CO2速率與動壓變化

在3種入口氣體流速下,z=0.205 mm,x=0.065 mm處3級模型CO2速率及動壓沿y方向的變化見圖4。入口氣體流速為1、0.1、0.01 mm/s時,流動時間分別取2、20、200 s。比較不同入口氣體流速的曲線發現,隨著入口氣體流速增大,CO2速率及動壓均隨之增大,但不改變CO2速率及動壓的變化趨勢。CO2動壓與速率的變化趨勢一致且具有對稱性,在中間位置的CO2動壓與速率最大,這是由于入口氣體在孔隙中流動,隨著孔隙變窄,氣體流速變大。

圖4 3級模型CO2速率及動壓沿y方向的變化

3.4 3種入口氣體流速下3級模型總壓力降變化

3種入口氣體流速下z=0,x=0處總壓沿y方向變化見圖5。入口氣體流速為1、0.1、0.01 mm/s時,流動時間分別取2、20、200 s。可見,3種入口氣體流速下總壓變化都呈相同的下降趨勢,入口氣體流速越大壓力降也越大,說明入口氣體流速對流場的壓力分布幾乎無影響,但會改變流場壓力的大小。圖5中間位置處壓力迅速降低,是由于中間氣體流速增大(見圖4)導致壓力急劇下降。壓力在y方向的分布曲線具有自相似性,整體呈現波動下降趨勢,局部波動的原因主要在于分形結構的不均勻性。3種入口氣體流速下的進出口總壓力降Δp分別為1.25、1.25×10-1、1.25×10-2Pa,可得總壓力降與入口氣體流速為線性關系:

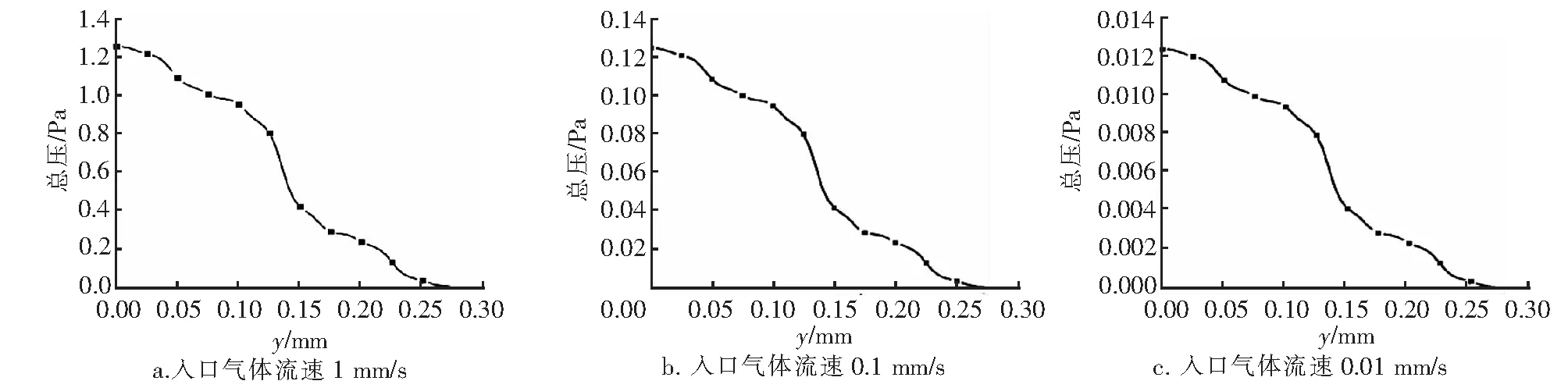
圖5 3級模型3種入口氣體流速下z=0,x=0處總壓沿y方向變化

Δp=1.25uin

式中 Δp——進出口總壓力降,Pa

uin——入口氣體流速,mm/s

4 結論

① 氣體在海綿結構中流動具有分形特性,CO2速率與動壓在不同級數模型中分布一致,具有明顯的對稱性與相似性,說明在分形維數相同的情況下,不同級數模型具有相同的分形特征。

② 通過對比3種入口氣體流速(1、0.1、0.01 mm/s)對二氧化碳體積分數分布的影響,可知入口氣體流速的增加有利于二氧化碳分布均勻,在允許的范圍內增加入口氣體流速有利于二氧化碳的吸附,提高LiOH吸附劑的吸附率。

③ 入口氣體流速的改變只能改變CO2動壓、CO2速率、總壓的值,不影響它們在流場內的分布。這是由Sierpinski-Menger海綿分形模型自身的分形特性決定,不受邊界條件的影響。可以得出總壓力降與入口氣體流速成線性關系。