對粗糙集上的不完全信息非合作博弈的均衡分析①

毛浪， 楊彥龍

貴州大學 數學與統計學院，貴陽 550025

博弈論又被稱為對策論, 是研究決策者在決策過程中所選擇的策略形成的不同局勢以及策略的均衡.在經典的博弈論理論中, 將博弈分為不完全信息博弈和完全信息博弈.不完全信息博弈是指在不充分了解其他參與人的特征、策略空間以及收益函數的情況下的博弈.

1965年, Zadeh發表的《模糊集理論》[1]為之后的模糊數學研究提供了系統的理論基礎.現如今模糊集理論已經應用到不動點理論、變分不等式和博弈論等許多領域[2-4].

1982年, 波蘭數學家Pawlak創立了粗糙集理論[5], 作為刻畫不完整性和不確定性的數學工具, 能有效地分析不精確、不一致、不完整等各種不完備的信息, 還可以對數據進行分析和推理, 從中發現隱含的知識, 揭示潛在的規律.因此, 粗糙集理論被廣泛使用在機器學習、數據挖掘、圖像處理、模式識別等許多領域.國內外針對模糊不完全信息的單獨博弈大都基于模糊集理論[6-9].目前利用粗糙集理論來解決博弈論中不確定性問題的研究相對較少[10-14].文獻[14]在文獻[11]的基礎上進一步分析不完全信息博弈的粗糙均衡并討論了不完全信息古諾博弈的粗糙均衡.本文在以上研究的基礎上給出了不完全信息博弈的粗糙均衡的存在性定理并對n人古諾博弈的粗糙均衡進行了討論.

1 預備知識

設U是論域,R是一等價關系, 則(U,R)稱為近似空間.設X是U的子集,x∈X?U, 則[x]R表示根據等價關系R構成的不可分辨元素的集合, 為R-元素集, 所有等價類集合記為ind(R).用U中所有具有屬性R的元素的集合來表達X時, 則有的元素一定屬于X, 而有的元素不一定屬于X.當給定近似空間(U,R), 對于每一個子集X和一個等價關系R, 可根據R的基本集合的描述來劃分集合X, 從而得出下近似和上近似的定義.

定義1[5]設X?U,R是一個等價關系, 那么當X可以由ind(R)中的集合的并表示時, 則X是R可定義的, 否則,X是R不可定義的.

定義2[5]若集合R-(X)={x|x∈U,[x]R?X}, 則稱R-(X)是X(X?U)的R-下近似集.

定義3[5]若R-(X)={x|x∈U,[x]R∩X≠?}, 則稱集合R-(X)是X(X?U)的R-上近似集.

定義4[5]令R-(X)={x|x∈U,[x]R?X}為下近似集,R-(X)={x|x∈U,[x]R∩X≠?}為上近似集.如果R-(X)=R-(X), 則稱X關于近似空間(U,R)是可定義的, 否則稱X關于近似空間(U,R)是粗糙的, 簡稱為粗糙集.

下近似表示根據等價分類R判斷一些元素(具有不可分辨性)組成的集合一定屬于X, 即[x]R中的元素根據等價分類R一定屬于X.上近似表示通過R, 一些元素組成的集合與X的交集非空, 即根據R其中有的元素可能屬于X, 有的元素可能不屬于X.上近似集和下近似集之差被稱為X的R-邊界集, 記為BNR(X)=R-(X)-R-(X).由于存在邊界區域, 集合中的某些元素既不能在全域的某個子集上被分類, 也不能在它的補集上被分類, 這就產生了不確定性.集合的邊界區域越大, 則精確度越低.

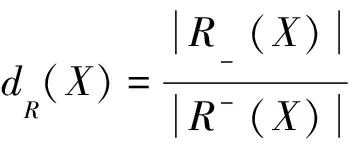
2 模型和Nash均衡的存在

下面先給出文獻[17]中經典的n人靜態貝葉斯博弈模型.記-i=N{i}為除了局中人i以外其他n-1個局中人.

古諾雙寡頭競爭經濟模型是不完全信息博弈的一個經典例子.在古諾雙寡頭競爭經濟模型中, 假設企業不知道其它企業是低成本還是高成本的, 但是假定一個企業知道其他企業類型的概率分布.為了更貼近現實情況, 假設Pi是不容易得到的, 因此, 在這種情況下, 貝葉斯博弈模型不再是合適的分析工具.粗糙集理論是建立在分類機制的基礎上的, 它將分類理解為在特定空間上的等價關系, 而等價關系構成了對該空間的劃分.基于粗糙集對于信息的分類作用并根據已知信息便能夠推斷出局中人類型(或是屬性)上的近似精確度.例如可以從公司的財務報表知道成本、盈利等信息, 并根據這些信息推斷出這個公司是成本低還是高)和是否是盈利型的.建立博弈模型如下:

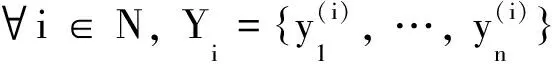
定義6若存在策略組合x*∈X滿足

則稱x*是博弈G的一個粗糙Nash均衡,

定理5設G={X1, …,Xn;Θ1, …,Θn;d1, …,dn;u1, …,un;Y1, …,Yn}是一個滿足以下條件的粗糙非合作博弈: 設?i∈N

(i)Xi是局部凸Hausdorff拓撲線性空間中的非空凸緊集,

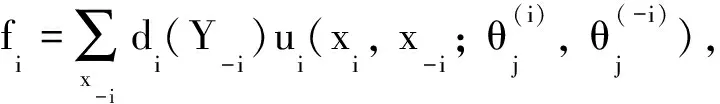
則G有一個Nash均衡.

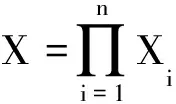
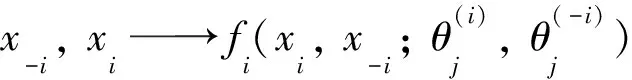
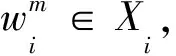
推論1當di(Y-i)=1時, 定理5與Nash均衡定理4是等價的, 此時為完全信息靜態博弈.

3 算例

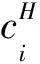
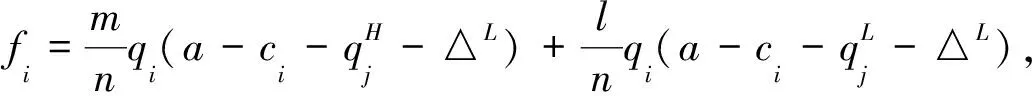
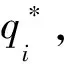
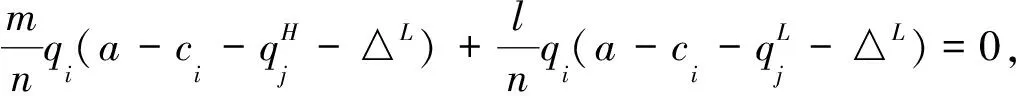
當企業i是低成本時有

當企業i是高成本時有

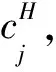
當企業j是高成本時有

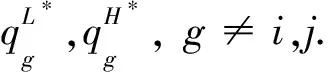
值得注意的是, 本文中僅討論了固定其他n-2個企業都是低成本的情況, 當然也可以假設其他n-2個企業的類型不相同或都為高成本, 這正好符合現實經濟的復雜性和變動性.

4 結論

本文研究了基于粗糙集上的不完全信息非合作博弈.證明了粗糙Nash均衡的存在定理.模型(B)是對模型(A)的一種擴展, 極大地保留了原始信息的客觀性, 具有更強的實用性和理論價值.本文僅研究了模型(B)的均衡解存在性問題, 對于其均衡解的穩定性研究將是下一步的工作.