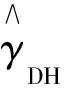極值指數(shù)的分布式矩率估計量①
羅心藝, 彭作祥
西南大學(xué) 數(shù)學(xué)與統(tǒng)計學(xué)院,重慶 400715
設(shè){Xn,n≥1}為獨立同分布的隨機變量序列, 其公共分布函數(shù)為F(x).若存在常數(shù)an>0,bn∈R使得對所有1+γx>0, 有
(1)
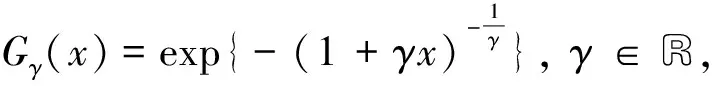
(2)
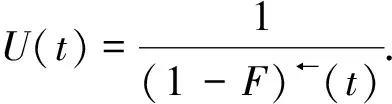
當(dāng)分布函數(shù)F未知時, 對極值指數(shù)γ的估計是極值理論的一個重要組成部分, 受到了學(xué)者的廣泛關(guān)注, 常用于金融、保險、自然災(zāi)害等領(lǐng)域.在分布函數(shù)形式未知的情況下, 文獻[1]提出了著名的Hill估計量, 推斷分布函數(shù)的尾部表現(xiàn); 文獻[2-4]在一定條件下證明了Hill估計量的相合性和漸近正態(tài)性; 文獻[5]提出了矩率估計量, 并給出了其分布表示; 文獻[6]提出了一系列基于二階參數(shù)的外部估計得到的漸近無偏估計量, 并證明了其漸近性質(zhì); 文獻[7]證明了包含Hill估計量和矩率估計量在內(nèi)的一系列尾指數(shù)估計量的漸近正態(tài)性.關(guān)于尾指數(shù)估計量的更多研究, 見文獻[8-10].
在大數(shù)據(jù)時代, 估計極值指數(shù)時, 常常會遇到被分開存儲的數(shù)據(jù), 例如分析來自不同保險公司的保險索賠時, 為了保護客戶的隱私, 保險公司不能向外部分享具體的數(shù)據(jù), 甚至不能分享任何索賠結(jié)果, 此時前文所提的Hill估計量和矩率估計量等都不可用.與大部分尾指數(shù)估計量的相關(guān)文獻一樣, Hill估計量等只使用了一部分秩序較高的統(tǒng)計量.文獻[11]和文獻[12]基于塊方法提出了DPR估計量.當(dāng)數(shù)據(jù)被分組儲存且每組只有少數(shù)幾個最大的樣本可用于分析時, DPR方法是可行的, 但是它僅使用了每塊中最大的兩個樣本, 很可能并不是尾指數(shù)的充分統(tǒng)計量.
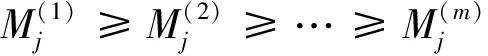
(3)
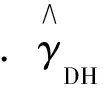
受文獻[13]啟發(fā), 本文基于矩率估計量提出如下分布式矩率估計量
(4)

(5)

(6)
1 相合性和漸近正態(tài)性


其中
(7)
2 定理的證明
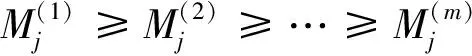
定理1的證明由文獻[14]的定理B.1.9知, 對x>1和t≥t0有,
(γ-ε)log((1-ε)x) (8) 則 (γ-ε)2(log((1-ε)x))2<(logU(tx)-logU(t))2<(γ+ε)2(log((1+ε)x))2 (9) 由(10)式和(11)式可得 (12) 由文獻[15]的引理3.4知 其中{Ej(i),i=1, …,d}服從獨立同分布的標準指數(shù)分布,j=1,…,k.因此 (13) (14) 對定理2的證明, 我們需要下面這個輔助引理. 引理1令Z(1)≥…≥Z(m)表示服從Pareto(1)分布的獨立隨機變量{Z1, …,Zm}的次序統(tǒng)計量, 則對任意ρ≤0, 有 證見文獻[13]的引理S.3. (15) (16) (17) 對ρ<0, 存在δ>0使得ρ+δ<0, 應(yīng)用不等式 可以得到 對于I2, 記 故 其后的證明方法與ρ<0的情況類似, 此處省略, 定理證畢. 本文提出了分布式矩率估計量, 下面將其與分布式Hill估計量進行有限樣本表現(xiàn)的比較.以γ=1,ρ=-1, 機器數(shù)量一定時, Burr分布的表現(xiàn)為例, 其分布函數(shù)為F(x)=1-(1+x)-1.隨機生成n個來自Burr分布的樣本, 存儲在k個機器中, 每個機器有m個觀測, 對每一個機器, 從m個觀測中選取d個超過數(shù)(d為自變量), 分別計算分布式Hill估計量和分布式矩率估計量的估計均值和均方誤差, 每個實驗重復(fù)s次并取平均值. 設(shè)置n=1 000,k=20,m=50,s=100,d的取值范圍為1,…,30, 模擬結(jié)果如圖1所示. 圖1 Burr(1)的分布式Hill估計量和分布式矩率估計量的估計均值及均方誤差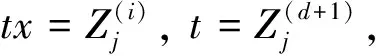







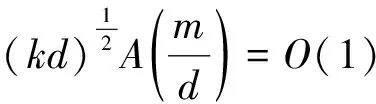



3 模擬研究