隨機格板方程的后向緊隨機吸引子①

韓凱利， 李揚榮

西南大學 數學與統計學院，重慶 400715

文獻[1-3]對隨機格系統做了深入的研究, 文獻[4-6]對吸引子的存在性和后向緊性做了研究并建立了相對完善的理論體系, 文獻[7-9]對格點方程的后向緊隨機吸引子進行了研究, 文獻[10-11]對板方程吸引子的存在性和連續性做了研究, 文獻[12]對帶有非線性噪音的格板方程做了研究, 本文將在文獻[10,12]的基礎上, 研究帶有乘法噪音的非自治隨機格板方程的后向緊隨機吸引子.

1 隨機格板方程

本文將在空間l2上討論帶有乘法噪音的非自治隨機格板方程

(1)

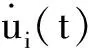
接下來做一些假設:

(Ⅰ)fi∈C1(R, R)且對所有的s∈R,i∈Z滿足:

|fi(s)|≤γ1|s|p-1+φ1,iφ1={φ1,i}i∈Z∈l2

(2)

fi(s)s≥γ2Fi(s)+φ2,iφ2={φ2,i}i∈Z∈l1

(3)

Fi(s)≥γ3|s|p-φ3,iφ3={φ3,i}i∈Z∈l1

(4)

|f′i(s)|≤γ4|s|p-2+φ4,iφ4={φ4,i}i∈Z∈l∞

(5)

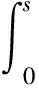
(6)

(Ⅱ)φi∈C1(R, R), 存在正數α1和α2, 使得

φi(0)=0α1≤φ′i(s)≤α2?s∈R,i∈Z

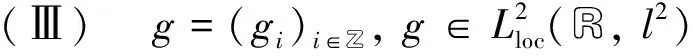
(7)

(8)

為了將方程(1)化簡, 定義從l2到l2上的算子如下:

(9)

且對于u=(ui)i∈Z∈l2和v=(vi)i∈Z∈l2, 有

‖A2u‖≤16‖u‖ (A2u,v)=(Au,Av)

(10)

為了證明隨機方程(1)產生一個隨機動力系統, 我們將其轉化為l2×l2上的一個隨機微分方程, 令

θtω(·)=w(·+t)-w(t)

則

是方程dz+kzdt=dW(t)的一個路徑解.

從文獻[13]可知, 隨機變量|z(ω)|是緩增的, 且滿足

(11)

則方程(1)可以重新改寫成具有隨機系數但沒有乘法噪音的等價方程

(12)

令E=l2×l2, 且有范數

其中‖·‖表示l2范數, 為了后續計算, 當λ+k2-α2k>0時, 定義一個新的范數‖·‖E:

容易驗證范數‖·‖E與范數‖·‖l2 ×l2是等價的, 且方程(1)的解產生的動力系統與通過方程(12)獲得的是一樣的, 因此我們只需要考慮方程(12)的解產生的動力系統.通過文獻[14]中關于解的存在性和唯一性的經典理論方法可以得到, 在假設(Ⅰ)下, 方程(12)在E上存在唯一的連續依賴于初始值的解

(u(t,ω,uτ),v(t,ω,vτ))T∈C([τ, +∞),E)

Φ(t,τ,ω,(uτ,vτ))=(u(t+τ,τ,θ-τω,uτ),v(t+τ,τ,θ-τω,vτ))

在下文中,D是E中所有后向緩增集構成的集族, 集合D={D(τ,ω)}∈D當且僅當

2 解的估計

引理1若假設(Ⅰ),(Ⅱ),(Ⅲ)成立, 則對任意后向緩增集D∈D, ?τ∈R,ω∈Ω,Ys-t∈D, 存在T=T(τ,ω,D,η)≥0, 使得

其中對?τ∈R,ω∈Ω, 有

證對任意固定的τ∈R,ω∈Ω,(us-t,vs-t)∈D, 將方程(12)中第二個等式與

v(r)=v(r,s-t,θ-sω,Ys-t)s≤τ

作內積, 有

αz(θr-sω)(3k-αz(θr-sω))(u,v)-(φ(v+αuz(θr-sω)-ku),v)+(g(r),v)

(13)

且有

v=ut-αuz(θr-sω)+ku

(14)

當α1-k>0時, 根據拉格朗日中值定理、假設(Ⅰ)-(Ⅱ)和Young不等式, 有

(15)

αz(θr-sω)(3k-αz(θr-sω))(u,v)-(φ(v+αuz(θr-sω)-ku),v)≤

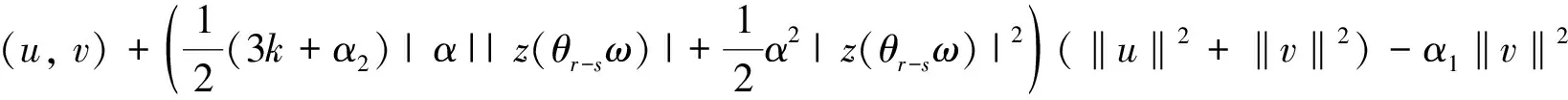
(16)

(17)

利用(6),(10),(14)式, 并將(15)-(20)式帶入(13)式, 整理有

(18)

其中

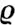
對(18)式利用Gronwall不等式, 計算可得

(19)

由文獻[10]可知, 當

時, 存在T1, 使得對?r≤-T1有

(20)

又因為|z(θrω)|是緩增的, 通過(7)式和(20)式, 可知

是收斂的.

因為D∈D,(us-t,vs-t)∈D(s-t,θ-tω),l2?lp, 則通過(6),(20)式, 對?t≥T1, 有

(21)

對(19)式關于s∈(-∞,τ]取上確界, 對?τ∈R,ω∈Ω,Ys-t∈D, 存在T=T(τ,ω,D,η)≥0, 當t≥T(≥T1)時, 有

(22)

推論1若假設(Ⅰ),(Ⅱ),(Ⅲ)成立, 且滿足引理1, 則由文獻[7,15]中拉回一致吸收集存在的條件可知, 協循環{Φ(t)}t≥0存在D-拉回后向一致吸收集K∈D, 其中

K0為拉回隨機吸收集.

引理2若假設(Ⅰ),(Ⅱ),(Ⅲ)成立,(us-t,vs-t)∈D(s-t,θ-tω),τ∈R,ω∈Ω,D∈D, 則對?η>0, 存在

T=T(τ,ω,D,η)>0N=N(τ,ω,η)≥1

使得對?t≥T, 方程(12)的解滿足

證定義一個光滑函數ρ, 當s∈R時, 有0≤ρ≤1, 且當|s|≤1時,ρ=0; 當|s|≥2時,ρ=1.則存在常數μ1, 對?s∈R, 有|ρ′(s)|≤μ1.

令

u=(ui)i∈Zv=(vi)i∈Z

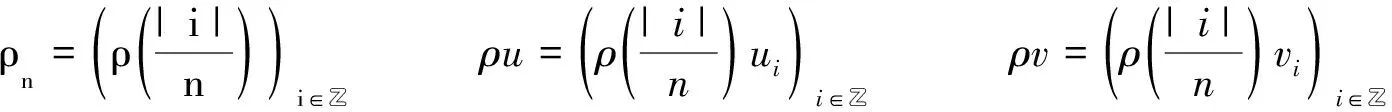
將方程(12)中的第二個等式與ρv作內積, 有

αz(θr-sω)(3k-αz(θr-sω))(u,ρv)-(φ(v+αuz(θr-sω)-ku),ρv)+(g(r),ρv)

(23)

當α1-k>0時, 通過Young不等式以及(14)式, 有

與文獻[12]的方法類似, 通過(9),(10),(14)式可知

(27)

將(24)-(27)式帶入(23)式, 并根據假設(Ⅰ),(Ⅱ), 整理有

(28)

對(28)式利用Gronwall不等式, 并取上確界, 計算可得

與(21)式類似, 可得

(29)

根據z(θrω)的緩增性和(11)式可知, 對?ε>0, 存在C=C(ε,ω), 使得

(30)

則通過(8),(20),(30)式可知, 存在常數M和T(≥T1), 當t>T時, 有

(31)

(32)

ηMC(ω)(1+R(τ,ω))≤η

(33)

所以通過(6),(29),(31)-(39)式, 對?η>0, 存在

T=T(τ,ω,D,η)>0N=N(τ,ω,η)≥1

使得對?t≥T, 有

引理3若假設(Ⅰ),(Ⅱ),(Ⅲ)成立, 則協循環{Φ(t)}t≥0在吸收集K∈D上是后向漸進緊的.

Yk=Φ(tk,τk-tk,θ-tkω,Yτ, k)=Y(τk,τk-tk,θ-τkω,Yτ,k)

下證{Yk}在E上是預緊的.由引理2可知, 存在K,N, 使得當k≥K時, 有

(34)

由引理1可知, {Yk}在E中是有界的, 因此{(Yk,i)|i|≤N}k在R2N+1中有界, 所以{(Yk,i)|i|≤N}k在R2N+1中有一個有限的ε-網, 結合(34)式可以得到{Yk}在E中有一個有限的2ε-網, 所以{Yk}在E中是預緊的, 進而{Φ(t)}t≥0在吸收集K上是后向漸進緊的.

3 后向緊隨機吸引子

定理1若假設(Ⅰ),(Ⅱ),(Ⅲ)成立, 則方程(1)生成的動力系統存在后向緊隨機吸引子.

證由推論1和引理3可知, 協循環{Φ(t)}t≥0存在D-拉回后向一致吸收集且在吸收集上是后向漸進緊的, 因此滿足文獻[15](定理3.9)中拉回吸引子的存在性條件, 因此方程(12)生成的非自治隨機動力系統Φ(t)存在唯一的后向緊D-拉回吸引子A∈D和唯一可測的D0-拉回吸引子A0∈D0.再根據文獻[16](定理6.1)可知A=A0, 所以吸引子A也是隨機的, 因此Φ(t)存在唯一的后向緊D-拉回隨機吸引子A∈D, 從而方程(1)存在后向緊隨機吸引子.