隨機Zakharov格點方程的后向緊隨機吸引子①

張琳， 李揚榮

西南大學 數學與統計學院，重慶 400715

若隨機吸引子的后向并是預緊的, 則稱該吸引子為后向緊隨機吸引子.文獻[1-6]研究了吸引子的存在性以及吸引子的后向緊性, 并建立了相對完善的理論體系.文獻[7-11]對隨機Zakharov格點方程的吸引子進行了研究.本文將在文獻[10]的基礎上, 研究帶有乘法噪音的隨機Zakharov格點方程的后向緊吸引子的存在性.

1 非自治隨機動力系統

本文將在l2×2空間上討論如下帶有乘法噪音的非自治隨機Zakharov格點方程:

(1)

其中α,λ,β,γ>0, Z是整數集

(W1,W2)是定義在度量動力系統(Ω,F, P, {θt}t∈R)上相互獨立的雙邊實值維納過程, 其中

Ω={ω=(ω1,ω2)∈C(R, R×R):ω1(0)=ω2=0}

F是Ω上由緊開拓撲生成的Borelσ-代數, P是(Ω,F)上的維納測度.在Ω上定義映射族

{θt}t∈R:θtω(·)=ω(·+t)-ω(t) (ω,t)∈Ω×R

°表示Stratonovich積分意義下的乘法噪聲.對于外力項

g(t)=(gk(t))k∈Zh(t)=(hk(t))k∈Z

有如下假設:

(2)

(3)

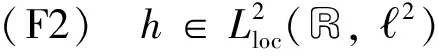
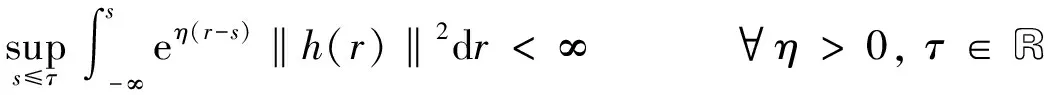
(4)

(5)

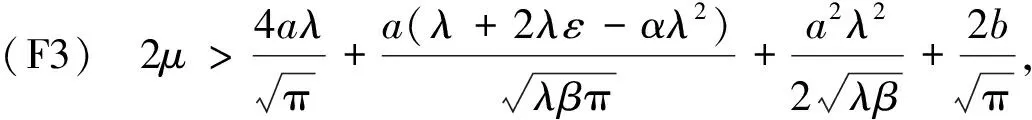
令

空間l2或2上的有界線性算子A的定義為

(Ab)k=2bk-bk+1-bk-1

(Bb)k=uk+1-uk(B*b)k=bk-1-bkb=(bk)k∈Z

則A=B*B=BB*, 并且滿足‖Bb‖2≤ 4‖b‖2.

對任意u=(uk)k∈Z,v=(vk)k∈Z∈l2,2, 定義空間l2和2上的內積和范數分別為

(u,v)λβ=λ(Bu,Bv)+λβ(u,v)

(φ1,φ2)=(u1,u2)λβ+(y1,y2)+(v1,v2)

令

(6)

(7)

則方程(1)可以轉化為以下等價形式:

(8)

令

令φ0=(u0,y0,v0)T, 則方程(8)可以改寫為如下簡單矩陣形式:

(9)

由文獻[8,10]可知, 若假設(F1)-(F3)成立, 對?T>0,φ0∈E, 方程(8)存在唯一的解φ(·,τ,ω,φ0)∈C([τ, +∞),E), 且依賴于初值φ0連續.因此方程(8)在(Ω,F, P, {θt}t∈R)上能生成一個連續的隨機動力系統{Φ(t)}, 對φ0∈E,t≥0,τ∈R,ω∈Ω, 有

Φ(t,τ,ω,φ0)=φ(t+τ,τ,θ-τω,φ0)

可以驗證Φ是一個非自治的隨機動力系統, 即滿足

Φ(0,τ,ω,·)=idΦ(t+s,τ,ω,·)=Φ(t,τ+s,θsω,·)°Φ(s,τ,ω,·)

在下文中, 設D是X中所有后向緩增集構成的集合, 若集合D∈D當且僅當

(10)

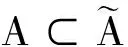
2 解的估計

引理1若假設(F1)-(F3)成立, 則對任意后向緩增集D∈D, ?τ∈R,ω∈Ω, 存在T=T(D,τ,ω)≥1, 使得當φs-t∈D(s-t,θ-sω)時, 有

(11)

其中

(12)

證對任意固定的τ∈R,ω∈Ω,φs-t∈D(s-t,θ-tω), 令

φ(r)=φ(r,s-t,θ-sω,φs-t)

其中s≤τ.φ(r)與方程(9)作內積, 可得

(13)

對于(13)式中的每一項, 利用H?lder不等式以及Young不等式, 可得

(14)

(15)

令

則由(13)-(15)式可得

(16)

對(16)式利用Gronwall不等式, 可得

(17)

由假設(F3)可得

對(17)式關于s∈(-∞,τ]取上確界, 結合(10)式可知, 存在T(D,s,ω)≥1, 使得當t≥T時, 有

因此(11)式得證, 即

引理2若假設(F1)-(F3)成立, 則對?η>0,(τ,ω,D)∈(R×Ω×D),φs-t∈D(s-t,θ-sω), 存在T(η,τ,ω,D)>0,k(η,τ,ω,D)≥1, 使得

證構造一個光滑函數ρ(s)∈C1([0, ∞),[0, 1]), 滿足: 當|s|≤1時,ρ(s)=0 ; 當|s|≥2時,ρ(s)=1; 當1≤s≤2時, 0≤ρ(s)≤1; 且|ρ′(s)|<ρ0,ρ0>0.令

其中

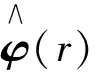
(18)

易證

則有

(19)

(20)

(21)

將(19)-(21)式代入(18)式, 可得

(22)

其中c1,c2,…,c9為常數, 對(22)式利用Gronwall引理, 可得

(23)

因為φs-t∈D(s-t,θ-tω)(s≤τ), 結合(10)式可得

(24)

由引理1和假設(F1)-(F3)可得, 存在T>0, 當t>T時, 有

(25)

(26)

(27)

(28)

因此, 由(25)-(28)式可得, 對?η>0,(τ,ω,D)∈(R×Ω×D),φs-t∈D(s-t,θ-tω), 存在T(ε,τ,ω,D)>0,k(ε,τ,ω,D)≥1, 使得

3 后向緊隨機吸引子

定理1若假設(F1)-(F3)成立, 則方程(1)所生成的動力系統存在后向緊隨機吸引子.

證因為{Φ(t)}t≥0滿足文獻[12](定理3.9)中的拉回吸引子的兩個存在性條件:

(i)非自治隨機動力系統 {Φ(t)}t≥0存在D-拉回隨機吸收集K∈D, 其中

K(τ,ω)={w∈E: ‖w‖2≤1+R0(τ,ω)} ?τ∈R,ω∈Ω

(ii)非自治隨機動力系統{Φ(t)}t≥0存在D-拉回后向一致吸收集K∈D, 其中

由文獻[4]可得, 非自治動力系統{Φ(t)}t≥0在吸收集K∈D上是后向緊的.因此方程(8)生成的非自治隨機動力系統Φ(t)存在唯一的后向緊D-拉回吸引子A∈D和唯一的可測D-拉回吸引子A∈D.再由文獻[13]中的定理6.1知A=A, 故吸引子A也是隨機的, 即Φ(t)存在唯一的后向緊D-拉回隨機吸引子A∈D.再由文獻[14-15]可知方程(1)與(8)生成的隨機動力系統共軛, 進而可得方程(1)存在后向緊隨機吸引子.