代理模型在飛行器多學科優化中的應用研究

蔣魯佳，辛萬青，張 鳴，王 威，陳紅波

(北京宇航系統工程研究所，北京 100076)

0 引言

多學科設計優化是為解決復雜系統設計困難提出的概念,通過實現多個學科的自動設計和優化能夠縮短產品研制周期、提高設計質量、降低研制成本,具有重要的研究意義和應用前景[1],盡管在很多領域得到了應用,并不斷向規范化、商業化發展,然而,在多學科設計優化過程中,大量的計算、學科之間復雜的數據交互以及學科分析中非線性響應都會消耗大量的計算時間,從而降低優化算法的尋優效率以及優化結果的準確性。

代理模型技術通過構造近似函數可以將復雜的學科分析簡化,從而避免了在優化過程中進行的極其耗時的多學科分析,從而降低了設計空間搜索的工作量。目前該技術已應用于風力渦輪機、巡航導彈頭部外形、運輸機機翼等優化設計中,并取得了較好的設計結果[2-4],此外,還有人提出了一些基于代理模型技術的優化算法,并驗證該方法能夠有效提升優化效率[5-6]。文中以飛行器多學科設計優化為例,探尋代理模型技術在其中應用的思路和方法。

1 代理模型原理

代理模型主要有多項式響應面模型、Kriging模型、徑向基函數模型以及人工神經網絡模型等。

1)多項式響應面模型

多項式響應面的前幾項數學表達式為:

(1)

式中:xi為m維自變量x的第i個分量;β0,βi,βij為待定參數。

多項式響應面模型具有良好的可微性和連續性,易于實現優化,且可以通過系數判斷各項對系統影響的大小[7],但是,在處理復雜程度較高的非線性問題時,多項式響應面模型預測和擬合的結果相對較差。此外,當建立模型的階數較高時,過擬合的情況也有可能發生[8]。

2)Kriging模型

Kriging模型一般表示為:

f(x)=g0(x)+z(x)

(2)

式中:g0(x)視作模型中確定的部分,可用多項式來表示;z(x)為漲落,是一個均值為0、方差為σ2的隨機函數。

Kriging模型處理復雜程度較高的非線性問題時,往往能夠取得較好的結果,但是構造模型所消耗的時間較長,且由于算法復雜,較難通過軟件實現,因此在實際使用中會受到一定限制[7,9-11]。

3)徑向基函數模型

徑向基函數的基本形式為:

(3)

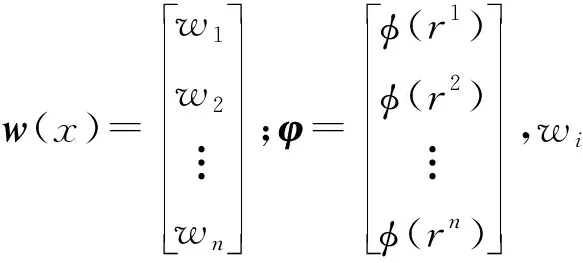
徑向基函數模型的基本思路是首先確定一組樣本點,然后再以這些樣本點為中心,以徑向函數作為基函數,通過把這些基函數線性疊加后計算待測點處的響應值[13],徑向基函數模型會根據選取徑向函數的變化而變化[14]。徑向基函數模型是一個結構相對簡單且計算量較小的代理模型[15-16]。

4)神經網絡模型

神經元的結構模型如圖1所示。

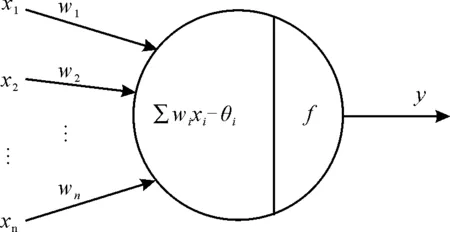
圖1 神經元結構模型Fig.1 Neuron structural model

其中,wi為神經元與輸入xi間的連接權重;θi為神經元的閾值;xi為神經元的輸入信號;f為傳遞函數[17]。

神經網絡模型使用輸入和輸出樣本訓練網絡,通過調節各層神經元之間的權系數,實現模型的構建。神經網絡模型建立的過程較其他代理模型更為簡單,且可以通過實現并行計算來提高效率[18-20]。

2 飛行器多學科設計建模

文中以飛行器為背景,采用由最小起飛質量和最大射程組成的多目標函數作為飛行器總體多學科設計優化的目標函數,并將影響該目標函數以及設計方案可行性的幾個專業,包括發動機結構及內彈道設計、飛行器外形設計、飛行氣動設計、飛行器結構設計、質量參數分析、飛行軌跡設計、姿控設計以及飛行載荷設計作為實現飛行器總體多學科設計優化集成的學科[21]。各學科使用方案論證階段的設計方法或能夠滿足該階段要求的工程計算方法建立各學科設計模型。通過封裝每個學科模型,使各學科成為具備獨立分析和設計能力的模塊。對建立的各學科設計模型的輸入、輸出數據進行分析,根據分析結果建立的飛行器總體多學科設計關系如圖2所示。

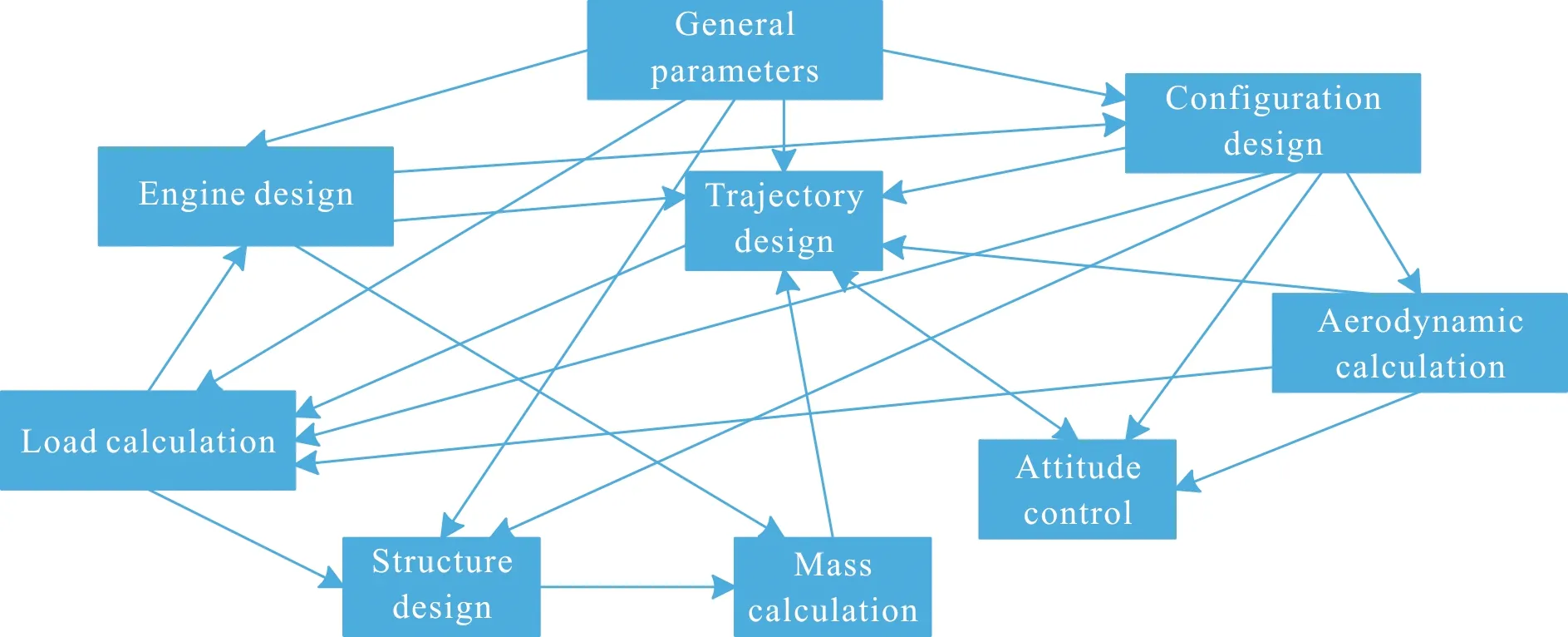
圖2 飛行器總體多學科設計關系Fig.2 Relationship of aircraft system design subjects

從圖2中可以看出多學科設計模型之間數據傳遞關系復雜,且存在多個反饋回路,而反饋回路會為飛行器總體多學科設計系統分析和優化帶來較大的困難,為此,采用多學科設計優化耦合關系處理方法[22]進行解耦,解耦后的飛行器總體多學科設計關系消除了原系統中存在的反饋回路,如圖3所示,系統在進行多學科分析時,只需由設計結構矩陣左上角的學科開始,依次進行分析即可[23]。

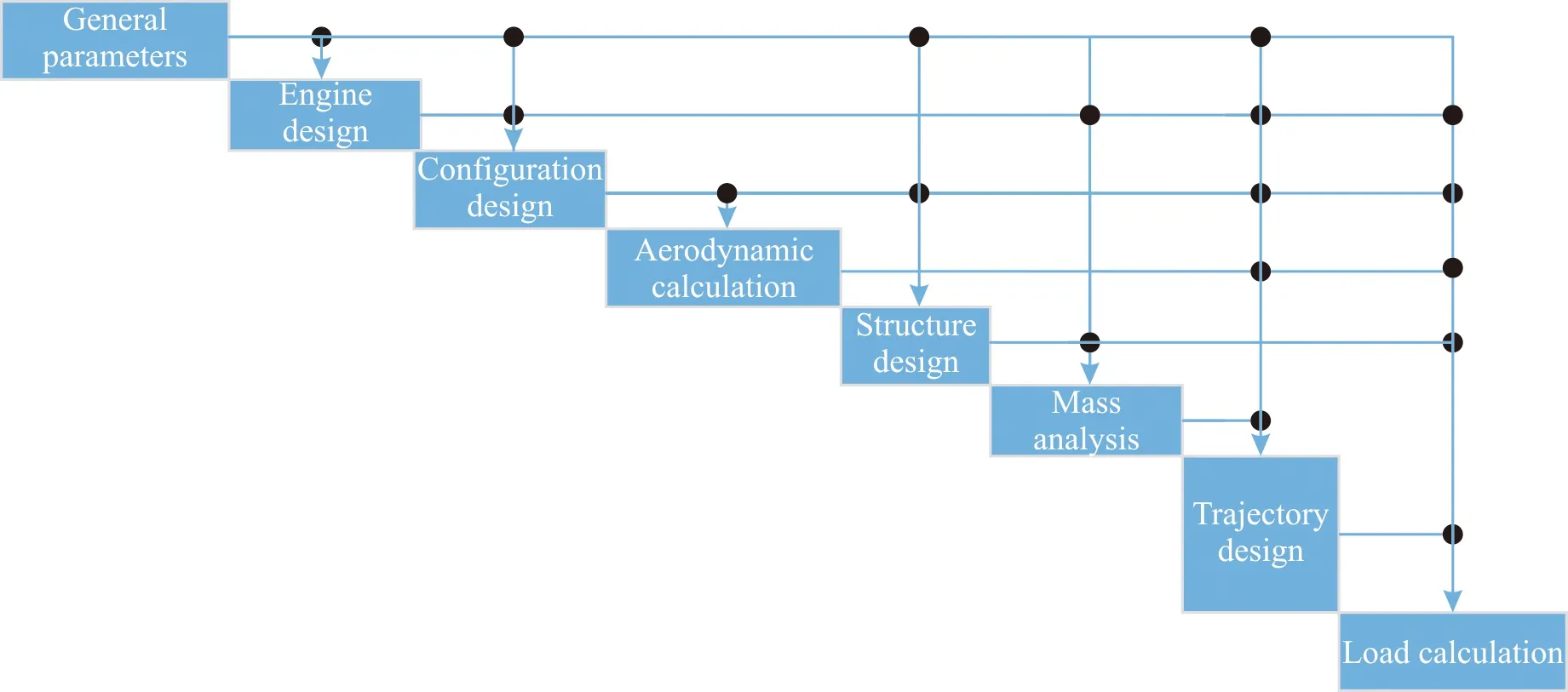
圖3 調整后的飛行器總體設計DSMFig.3 DSM of aircraft system design after adjustment

使用iSIGHT-FD軟件平臺對飛行器總體多學科設計進行集成,集成的流程圖和數據關系分別如圖4和圖5所示[24]。

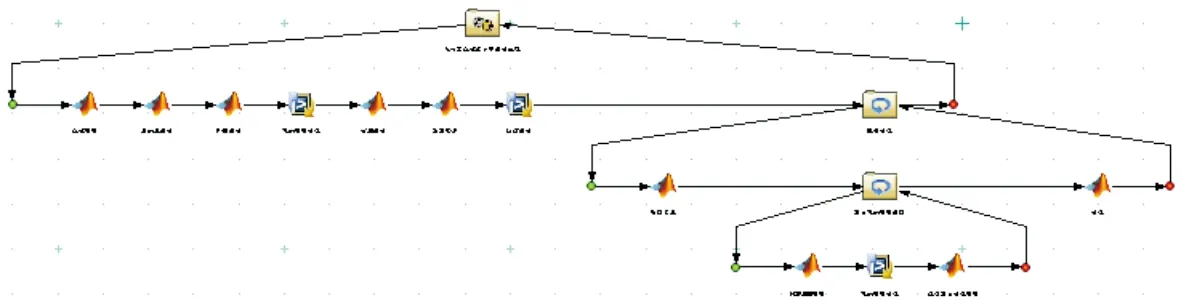
圖4 飛行器總體多學科設計集成的流程圖Fig.4 Flow chart of integrated aircraft system multidisciplinary design

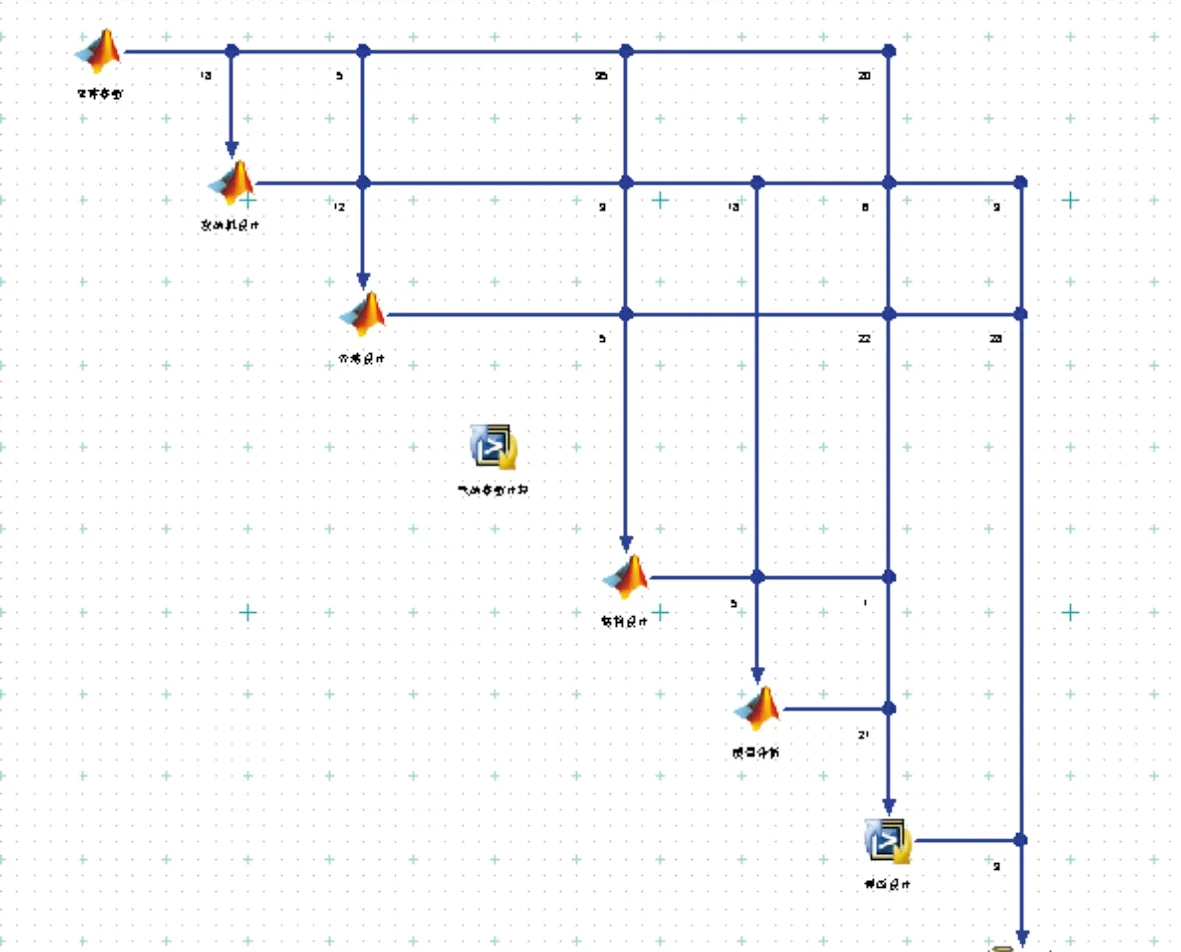
圖5 飛行器總體多學科設計集成數據關系Fig.5 Relationship of integrated aircraft system multidisciplinary design

3 飛行器多學科設計優化

采用非支配遺傳算法對建立的飛行器總體多學科設計優化模型的設計空間進行搜索,設置的種群數量為50,迭代次數為50,交叉概率為0.9,模型運行共耗時91 h9 min51 s,平均每次迭代用時約2 min11 s,得到的優化結果如圖6所示,其中,縱坐標代表飛行器航程,橫坐標代表飛行器起飛質量,圖中隱去各坐標軸的度量(下同),圖中藍色的點即為Pareto解集,紅色的點為滿足各種約束條件的可行解集。

圖6 優化結果Fig.6 Result of optimization

由以上優化結果可以看出,Pareto解集大致形成了一個Pareto面,由于Pareto解集中的點是由優化迭代范圍內的非劣解集組成,因此,所有可行解包括優化的初始點都在這個Pareto面的右下方。在縱軸或橫軸的任意位置畫一條與橫坐標軸或縱坐標軸平行的直線,該直線與Pareto面的交點就是在射程一定的條件下起飛質量最小的單目標優化問題或在起飛質量一定的條件下射程最大的單目標優化問題的最優解,Pareto解集也正是由這些“起飛質量一定的最大射程”或“射程一定的最小起飛質量”單目標優化問題的最優解組成。

通過對優化結果分析發現,飛行器總體多學科設計優化Pareto解集中兩個端點設計變量的變化非常小,特別是一些外形參數變化都是在1～5 mm左右,這對于工程設計來說,只相當于在實際生產制造過程中產生的誤差,最終得到的起飛質量和射程目標函數也非常的接近。經進一步分析可知,雖然耗費了大量的計算時間,進行了2 500次迭代計算,也得到了Pareto解集,但這僅是在2 500次迭代結果中得到的Pareto解集,迭代次數與設計空間上的可行解集相比還是非常有限的,盡管選擇的非支配排序遺傳算法在設計空間上具有全局搜索的能力,即理論上只要有充足的時間一定可以得到最優的Pareto解集,但是平均每次迭代需要耗費2 min11 s的模型,要進行全局搜索消耗的計算時間是非常巨大的。

對于建立的飛行器總體多學科設計優化模型存在的分析時間長、計算量大的問題,在當前計算機發展水平下,采用直接優化的方法獲得全局最優解還存在一定的困難。為此,提出使用代理模型對復雜的多學科設計模型進行近似,并基于此開展優化設計的方法。

4 基于代理模型的飛行器多學科設計優化

將飛行器總體多學科設計優化模型中各學科分析模型作為一個整體建立代理模型,即在不考慮其內部各學科設計模型的輸入輸出以及各學科之間數據傳遞關系的條件下,建立飛行器總體多學科設計模型的代理模型。

首先使用了典型樣本點分別采用響應面代理模型和神經網絡代理模型對飛行器總體多學科設計模型進行近似。構造的四階響應面代理模型和神經網絡代理模型誤差分析部分結果分別如圖7、圖8所示,其中,左側“Total Error”列為構造代理模型所有對應的樣本點平均誤差歸一化后的數值,右側響應圖則清晰的表達了代理模型響應變量偏離實際值的情況。

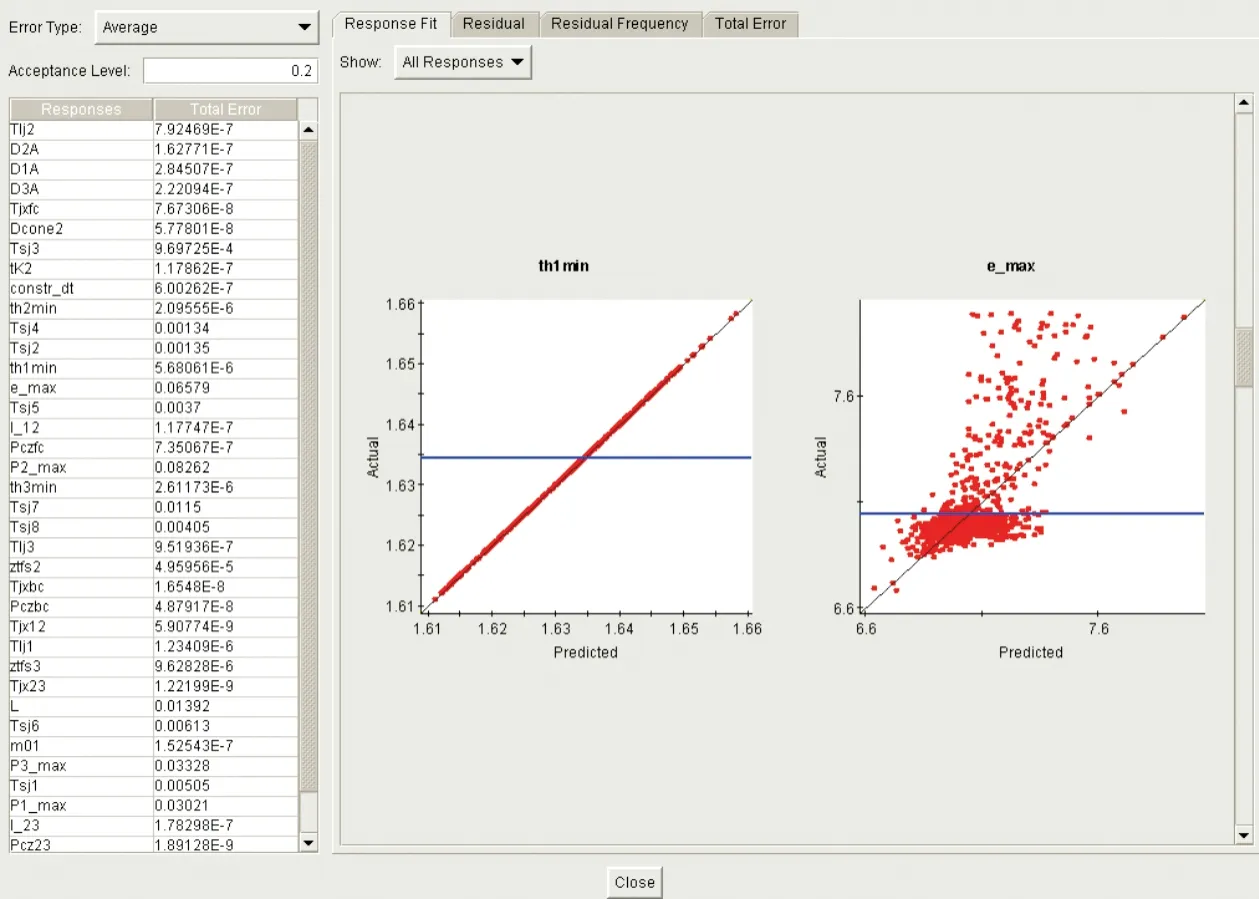
圖7 四階響應面代理模型誤差分析Fig.7 Error analysis of quartic RSM

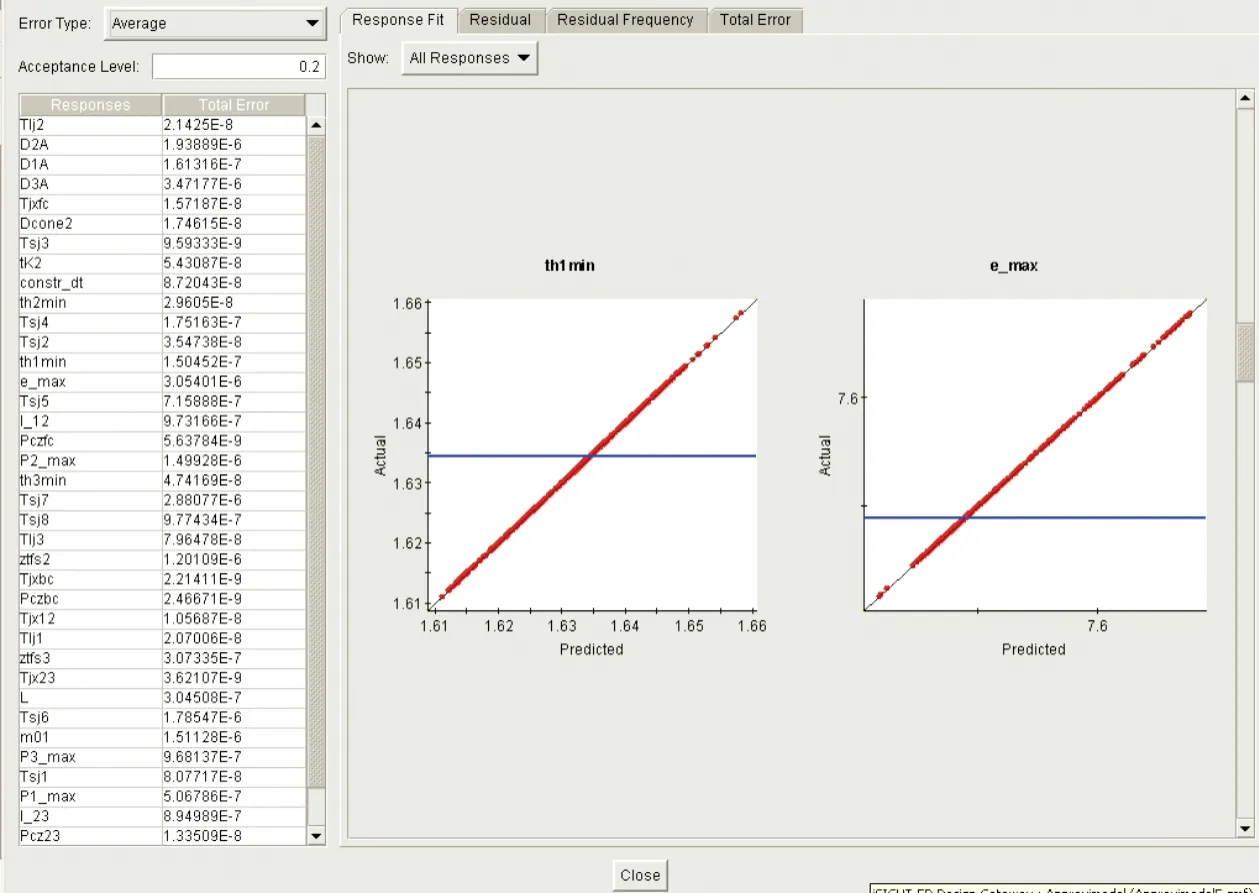
圖8 神經網絡代理模型誤差分析Fig.8 Error analysis of RBF model

由以上誤差分析對比可以看出,由于建立的飛行器總體多學科設計模型較為復雜,采用響應面法構造的代理模型誤差較大,已經不能很好的反映原模型的真實情況;而采用神經網絡構造的代理模型,雖然模型文件規模較大,但能夠對樣本點實現較好的近似,為此,選擇神經網絡代理模型實現對原模型的近似。

為了使樣本點集具有良好的散布均勻性,并在取值范圍內能夠以較少的組合方式獲得設計空間較全面的認識,使用最優拉丁超方設計方法進行了DOE(design of experiment)實驗[25],并將該實驗結果作為構造代理模型的樣本點,并通過訓練完成飛行器總體多學科設計神經網絡代理模型的構造。然后,再對構造的代理模型進行優化,共耗時約2 h,進行了40 000次迭代,得到的Pareto解集如圖9所示。從圖中可以明顯的看出起飛質量與射程的變化趨勢,即隨著裝藥量的增加,獲得的射程也越大。其中,起飛質量在變化的過程中存在一個跳變,這可能是由于在構造代理模型樣本點不夠充分引起的。

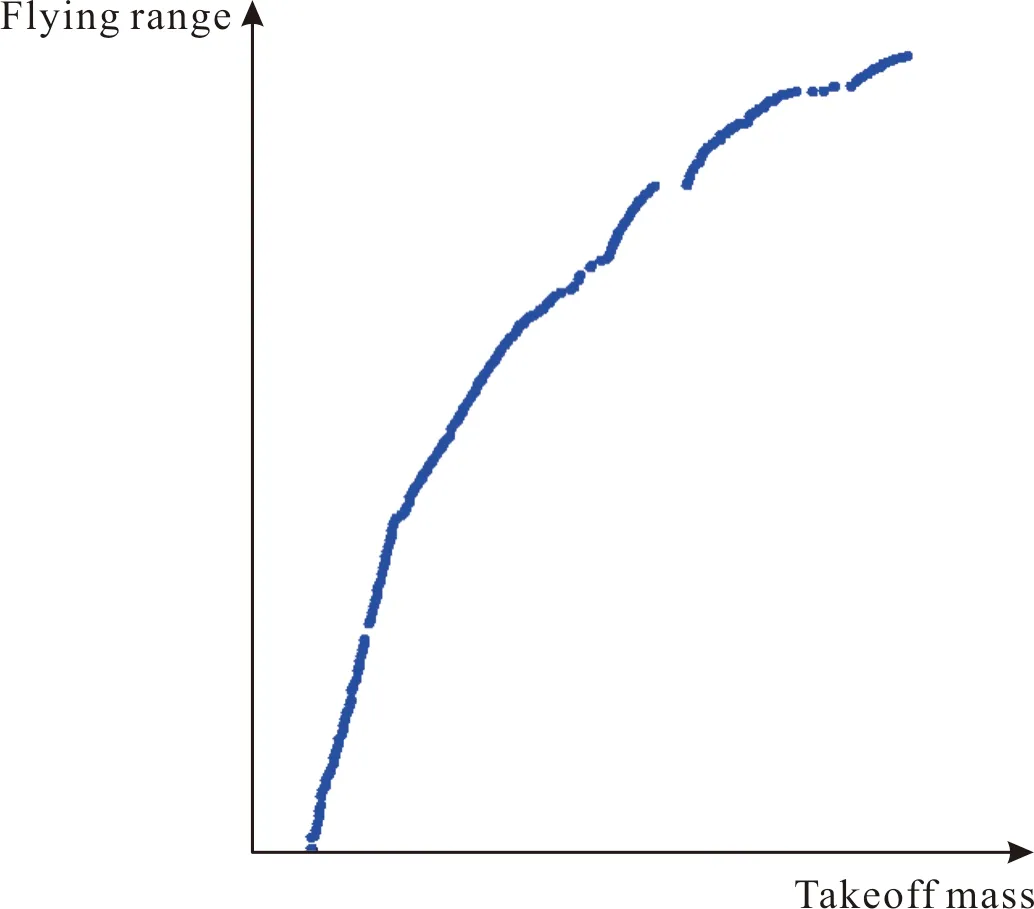
圖9 代理模型優化結果Fig.9 Result of surrogate model optimization

在Pareto解集中選取了某起飛質量下的設計結果,并將該結果重新在飛行器總體多學科設計模型中進行分析計算,得到該起飛質量下的最大射程設計結果。通過比對發現,基于代理模型的飛行器多學科設計優化結果較原來的設計結果將最大射程提高了約6%,較好的說明基于代理模型的飛行器多學科設計優化在大幅提升優化效率的同時,還能夠充分利用各學科模型相互作用產生出來的協同效應,進一步挖掘設計潛力[26-27]。

5 結論

文中針對飛行器總體多學科、多目標、多約束優化設計帶來的計算困難問題,首先對復雜多學科優化問題計算困難進行了分析;其次提出一套使用代理模型技術實現飛行器總體多學科設計優化的思路和方法;然后提出使用代理模型將飛行器總體多學科設計模型作為一個整體進行近似的方法;最后提出了使用最優拉丁超方設計方法對設計空間進行DOE實驗,并將實驗結果作為建立代理模型的樣本點的方法。優化結果表明,該方法可以有效降低多學科設計優化問題的復雜性,提高優化效率。

構造代理模型進行優化能夠縮短計算需要的時間,雖然優化結果與原優化模型存在一定差距,但是隨著構造代理模型的樣本點增加,理論上能夠在一定精度范圍內反映設計變量與目標函數之間的大致關系,為設計人員權衡折衷、初步選擇初始設計參數提供參考。此外,將代理模型的優化結果作為精確模型的初始設計點進行優化,也能夠加快整個優化過程的收斂速度。