基于VB-AUKF的GNSS/SINS組合導航信息融合算法

孫玉梅，潘新龍，王美春

(1 濰坊科技學院計算機學院，山東 濰坊 262700；2 海軍航空大學，山東 煙臺 264001)

0 引言

經典線性卡爾曼濾波采用線性高斯狀態空間模型,是GNSS/SINS組合導航系統經常采用的信息融合方式[1]。當系統的非線性比較嚴重時,擴展卡爾曼濾波(EKF)的估計不準確,而無跡卡爾曼濾波(UKF)可以降低EKF線性化帶來的誤差,可以將組合導航系統擴展到非線性濾波模型[2]。然而,UKF方法的一個嚴重缺陷是假設準確的系統模型及已知的先驗噪聲統計特性,而這個假設在實際環境下不成立[3]。

自適應濾波是解決上述問題的有效方法,在估計系統狀態參數的同時也可以估計噪聲統計特性。而貝葉斯方法是目前最普遍應用的方法,包括協方差匹配法、極大似然法均為貝葉斯方法的近似方法[4]。而變分貝葉斯方法具有較低的計算成本,可以近似求解貝葉斯方法中高度耦合的高維隱變量的后驗推理,近年來在諸多領域得到應用,如情報監測[5]、目標跟蹤[6]、雷達系統[7]等。

近年來,將變分貝葉斯方法與線性卡爾曼濾波技術相結合而形成的VB-KF算法在組合導航系統也得到較深入的研究[8]。如:文獻[8-9]將VB-KF技術應用于GNSS/SINS組合導航系統;文獻[10]、文獻[11]分別將VB-KF技術應用于同步與異步多傳感器組合導航系統;針對VB-KF技術對噪聲跟蹤性能差的問題,文獻[12-13]提出了基于T分布的變分高斯濾波算法,但是該方法將量測噪聲建模為T分布、導致不能單獨調節噪聲方差內獨立變化的噪聲。同時,上述文獻的共同特點是采用線性卡爾曼濾波方法,無法有效解決模型誤差導致的濾波精度下降問題。

為此,文中將變分貝葉斯方法與UKF算法相結合,在對GNSS/SINS組合導航系統進行變分貝葉斯自適應UKF非線性濾波建模的基礎上,提出了量測噪聲方差自適應估計的迭代模型。

1 變分貝葉斯估計模型

對于狀態方程非線性而量測方程線性的離散時間非線性系統[10]:

(1)

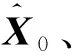
對于式(1)模型,如果Rk是時變的或未知的,則貝葉斯最優濾波的目標是計算系統狀態和量測噪聲方差矩陣的聯合后驗分布p(Xk,Rk|Z1∶k),此時該濾波過程包含以下步驟[14-15]:

1)初始化:計算系統狀態和量測噪聲方差矩陣的先驗分布p(X0,R0)。

2)預測:系統狀態向量Xk與測量噪聲方差矩陣Rk的聯合預測分布由Chapman-Kolmogorov方程給出[16]:

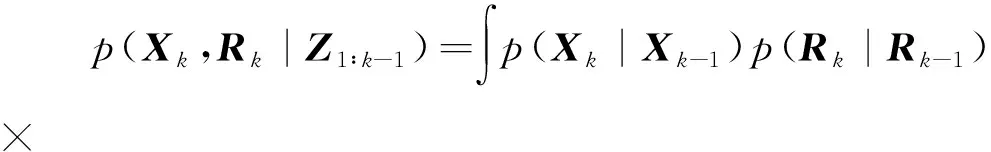
(2)

3)更新:給定下一個測量值Zk,通過貝葉斯規則將上述預測分布更新為后驗分布:

p(Xk,Rk|Z1∶k)∝p(Zk|Xk,Rk)p(Xk,Rk|Z1∶k-1)

(3)

式(2)、式(3)所涉及的積分通常是無法解析處理的,可利用后驗變分近似表示為[17]:

p(Xk,Rk|Z1∶k)=QX(Xk)QR(Rk)

(4)

其中:

(5)

式(5)中兩個方程相互耦合,為此,對兩個方程的期望進行評估及參數匹配,得到密度:

(6)

則式(2)、式(3)變為[16]:

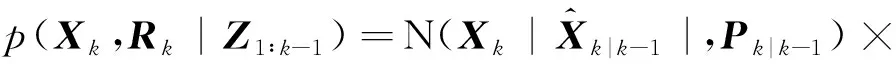
(7)

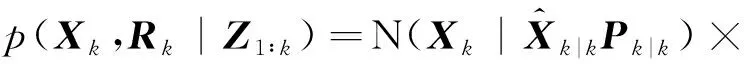
(8)

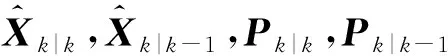
(9)

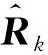
(10)

為了使觀測噪聲的變化規律具有自適應調整特性,引入因子ρi∈(0,1]。對于i=1,2,…,d,則有[16]:

(11)

2 基于變分貝葉斯的組合導航UKF算法

2.1 變分貝葉斯UKF算法

根據系統模型,將標準UKF算法與變分貝葉斯估計模型相結合,得到組合導航系統的基于變分貝葉斯的自適應UKF算法(VB-AUKF):

對于式(1)所示的非線性系統,將系統狀態和系統噪聲進行合并,得到增廣狀態向量:

(12)

式中:χa,χX和χW分為Xa,Xk和Wk的采樣點向量,假設其維數分別為N,Lx,Lw,則N=Lx+Lw。

步驟1:初始化

(13)

步驟2:樣點計算

(14)

(15)

其中:λ=α2(N+κ)-N;α,β和κ為比例因子。

步驟3:時間更新

(16)

(17)

(18)

其中:ρ=[ρ1ρ2…ρd]T;α=[α1α2…αd]T;β=[β1β2…βd]T。

步驟4:量測更新

(19)

(20)

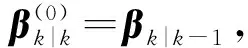
(21)

(22)

(23)

(24)

式(21)～式(24)中,1≤j≤J。

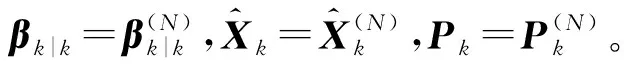
2.2 GNSS/SINS組合導航系統模型

GNSS/SINS組合導航系統非線性濾波的狀態方程采用SINS的力學方程,組合導航系統的導航參數直接選取為被估計的狀態。選取“東北天”地理坐標系為導航坐標系,則連續時間系統的狀態方程為:

(25)

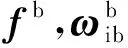
選取GNSS接收機輸出的三維速度和三維位置直接作為觀測向量,則量測方程可以表示為:

(26)

對式(25)、式(26)進行離散化處理可以得到離散化的狀態方程及量測方程。

3 仿真結果與分析

在Matlab環境下進行仿真,首先評估參數ρ,α,β的取值對量測噪聲未知均方差估計的影響,然后評估GNSS/SINS組合導航系統VB-AUKF算法的濾波性能。

3.1 仿真條件

以飛行器作為仿真對象,其飛行過程包含各種機動運動。初始位置為(118°E,29°E,50 m),仿真時間為3 600 s;濾波周期為1 s。初始參數設置如表1所示。

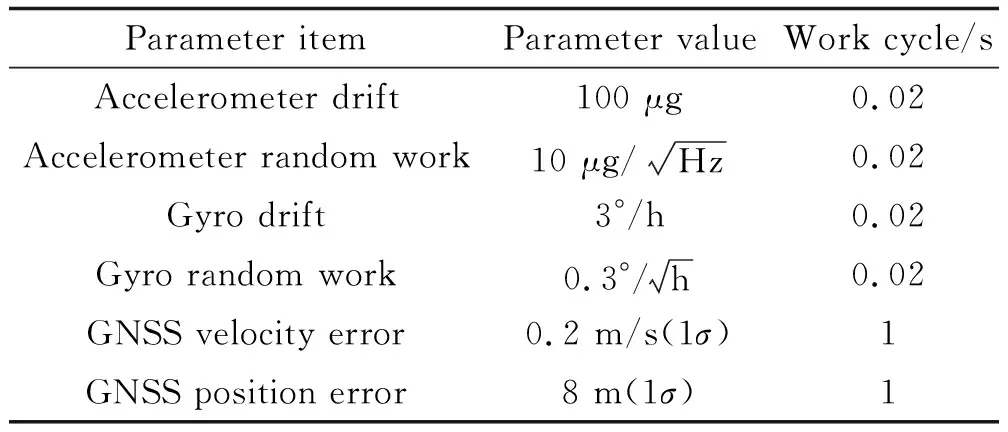
表1 導航傳感器誤差參數設置Table 1 Navigation sensor error parameter setting

根據表1所示的GNSS誤差設置,則正常情況下GNSS量測噪聲的均方差為:

rroot=sqrtm(R)=diag([0.2 0.2 0.2 8 8 8])

(27)

其中函數sqrtm(·)的功能是對矩陣中每個元素取開平方。

為了驗證系統算法性能,在飛行器飛行期間設定GNSS量測噪聲均方差變化為:

(28)

3.2 仿真校驗

以下的仿真實驗均是以相同的導航仿真原始數據為基礎,對式(21)～式(24)的迭代步數取j=2。

3.2.1 參數ρ對未知方差估計的影響

為了評估ρ對量測噪聲未知方差估計精度的影響,首先使得α,β的取值不變并設定為:

(29)

對參數ρ的取值,定義方案A:

方案A1:ρ=[0.85 0.85 0.85 0.85 0.85 0.85]

方案A2:ρ=[0.90 0.90 0.90 0.90 0.90 0.90]

方案A3:ρ=[0.95 0.95 0.95 0.95 0.95 0.95]

方案A4:ρ=[1 1 1 1 1 1]

方案A5:ρ=[0.99 0.99 0.99 0.99 0.99 0.99]

基于上述5種方案,圖1～圖2為利用文中算法估計到的位置誤差及速度誤差均方差曲線。

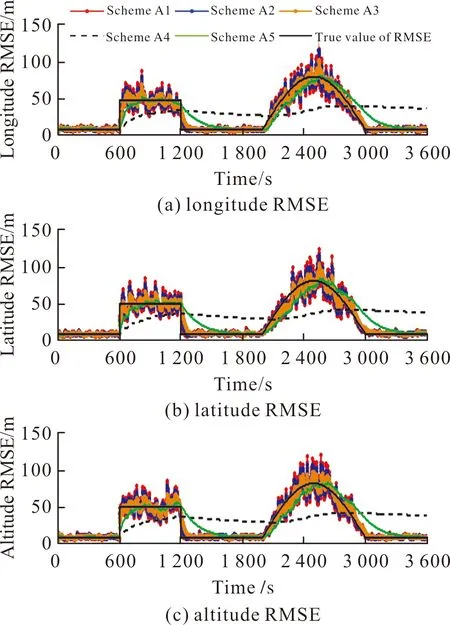
圖1 GNSS位置噪聲均方差估計曲線Fig.1 GNSS position noise RMSE estimation curve

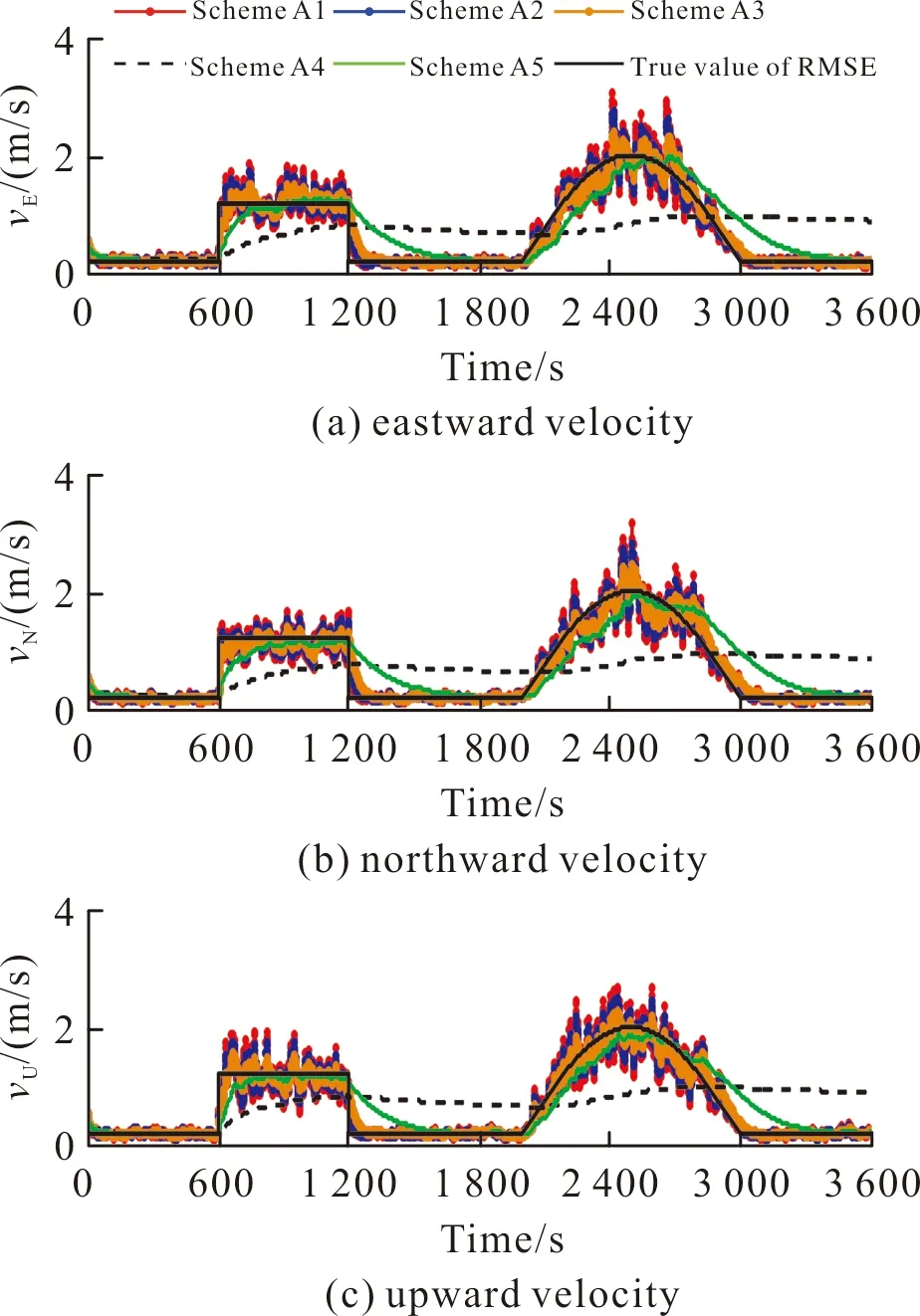
圖2 GNSS速度噪聲均方差估計曲線Fig.2 GNSS velocity noise RMS estimation curve

由圖1～圖2可見,當ρ中的元素ρi=1(i=1,2,…,d;d=6)時,變分貝葉斯算法適合于估計平穩噪聲的均方差(方案A4);ρi<1并接近于1時,文中算法估計的量測噪聲均方差在實際均方差變化結束時存在較嚴重的“拖尾”現象(方案A5);當ρi<0.9時,估計到的均方差能較精確地反映實際均方差的變化規律,但是估計曲線波動幅度隨著ρi的減小而增大(方案A1、方案A2)。

實驗證明,當0.95≤ρi≤0.97時,文中算法估計到的均方差效果較好,不僅能反映實際均方差的變化規律,而且估計曲線波動幅度較小(方案A3)。

3.2.2 參數α對未知方差估計的影響

為了評估α對量測噪聲未知方差估計精度的影響,首先使得ρ,β的取值不變并設定為:

(30)

方案B1:α=[1 1 1 1 1 1]

方案B2:α=0.2×[1 1 1 1 1 1]

方案B3:α=5×[1 1 1 1 1 1]

基于上述3種方案,圖3～圖4為利用文中算法估計的位置誤差及速度誤差均方差曲線。

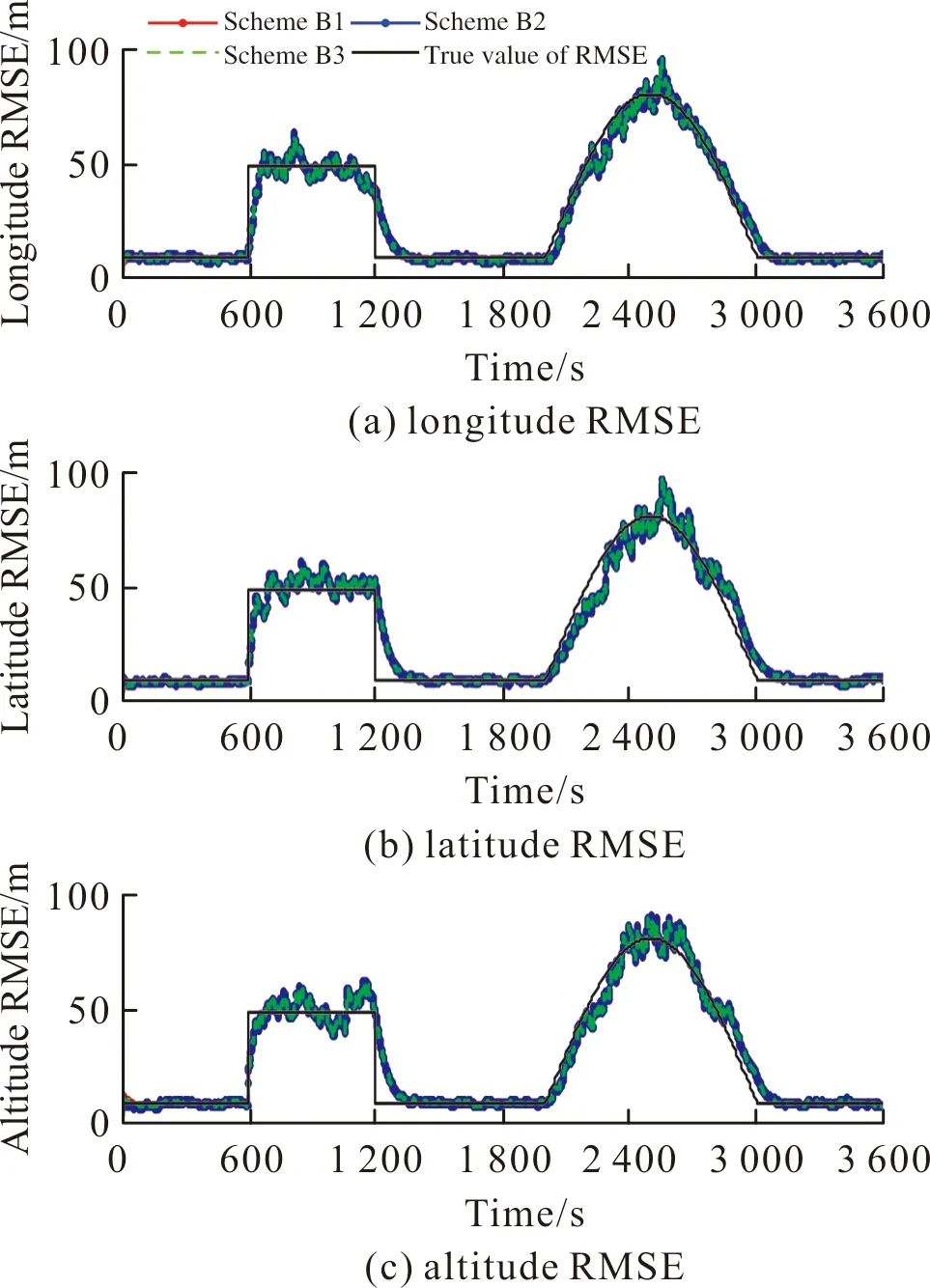
圖3 GNSS位置噪聲均方差估計曲線Fig.3 GNSS position noise RMSE estimation curve

圖4 GNSS速度噪聲均方差估計曲線Fig.4 GNSS velocity noise RMSE estimation curve

由圖3～圖4可以看出,當ρ,β不變時,α的選擇僅僅改變均方差的初始估計值,經過短時間后α的選擇對均方差的估計值無影響。

3.2.3 參數β對未知方差估計的影響

為了評估β對量測噪聲未知方差估計精度的影響,首先使得α,ρ的取值不變并設定為:

(31)

方案C1:β=[0.3 0.3 0.3 6 6 6]

方案C2:β=3×[0.3 0.3 0.3 6 6 6]

方案C3:β=[0.02 0.02 0.02 32 32 32]

基于上述3種方案,圖5～圖6為利用文中算法估計的位置誤差及速度誤差均方差曲線。

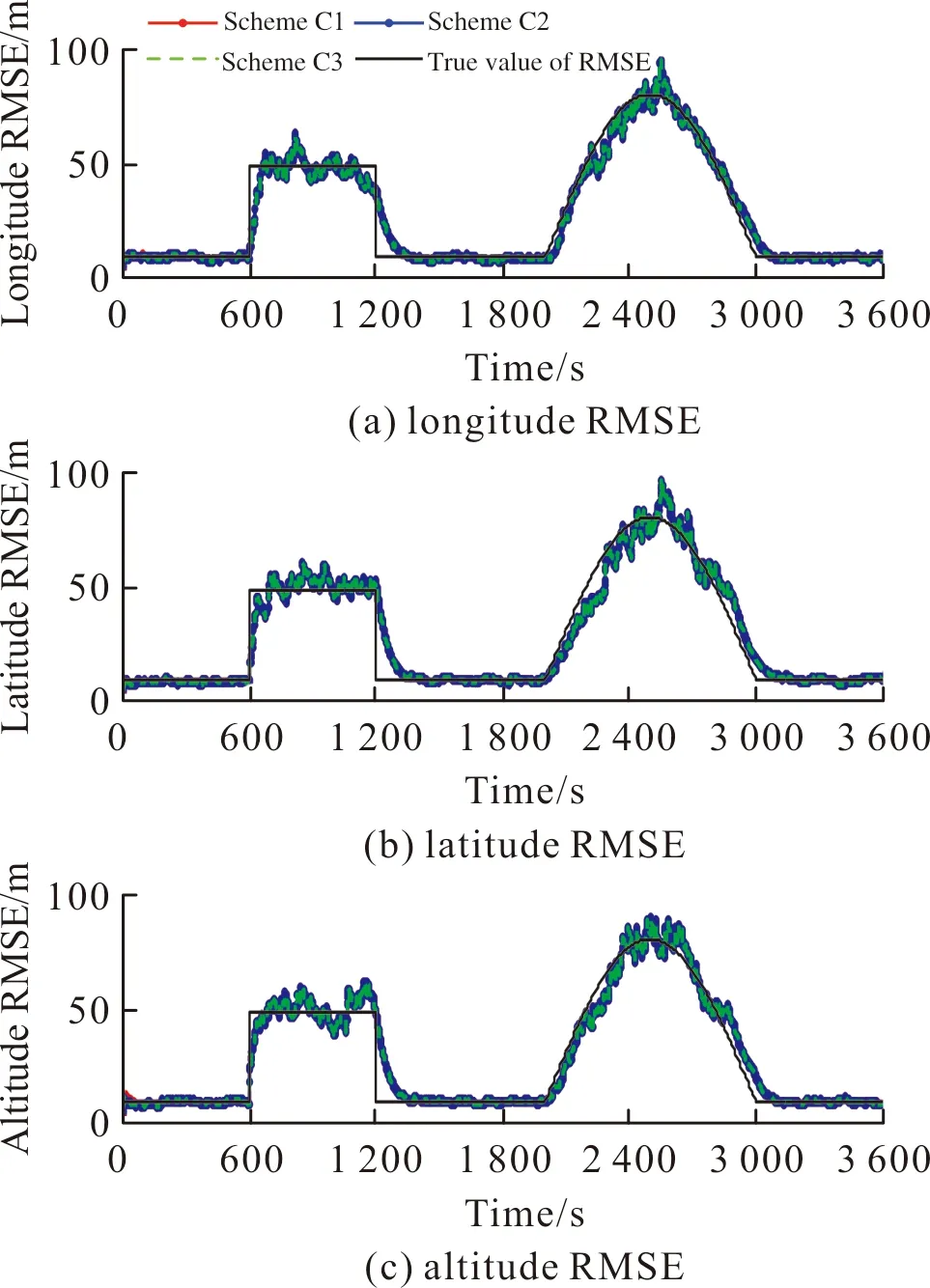
圖5 GNSS位置噪聲均方差估計曲線Fig.5 GNSS position noise RMSE estimation curve

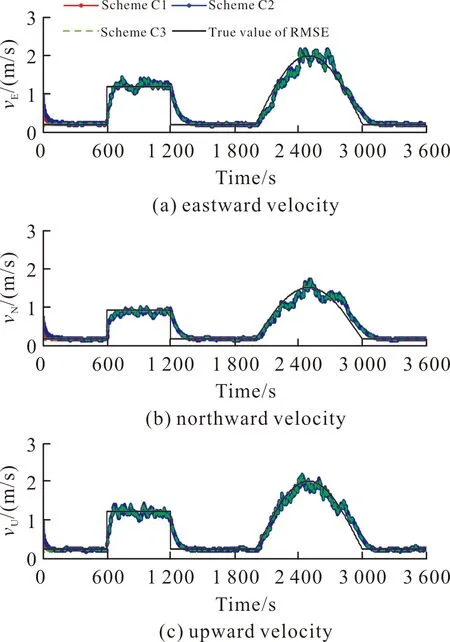
圖6 GNSS速度噪聲均方差估計曲線Fig.6 GNSS velocity noise RMSE estimation curve

由圖5～圖6可以看出,當α,ρ不變時,β的選擇也僅僅改變均方差的初始估計值,經過短時間后β的選擇對均方差的估計值無影響。

同時,綜合對比圖1～圖6,可以看出,當ρ的值不變時,α和β值的選擇僅僅改變了均方差的初始估計值,經過短時間后α和β值的選擇對均方差的估計值無影響;對均方差估計結果影響的決定參數是ρ。所以,只要ρ的取值處于合理區域,文中算法估計到的量測噪聲均方差具有較好的穩定性。

3.2.4 基于VB-AUKF的組合導航實驗

圖7～圖9給出了基于標準UKF算法及文中算法方案15的組合導航系統位置誤差、速度誤差及姿態誤差曲線對比圖。由圖7～圖9可以看出,由于標準UKF算法對量測噪聲均方差無自適應調節能力,所以當量測噪聲均方差發生變化時標準UKF算法得到的導航參數誤差較大;而文中算法由于對量測噪聲均方差的自適應調節能力較強,故可以保證系統的濾波精度。

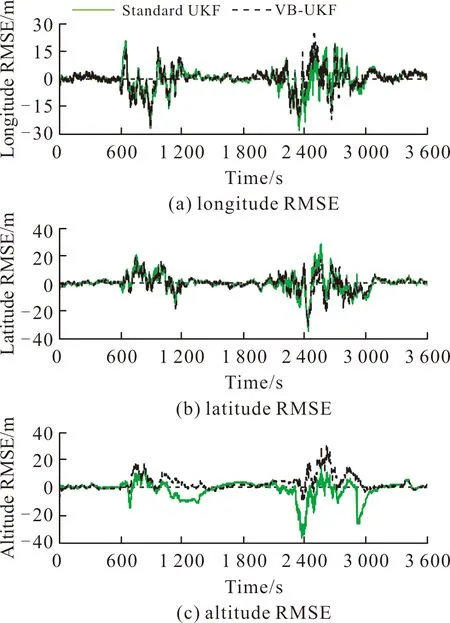
圖7 位置誤差曲線對比圖Fig.7 Position error curve comparison

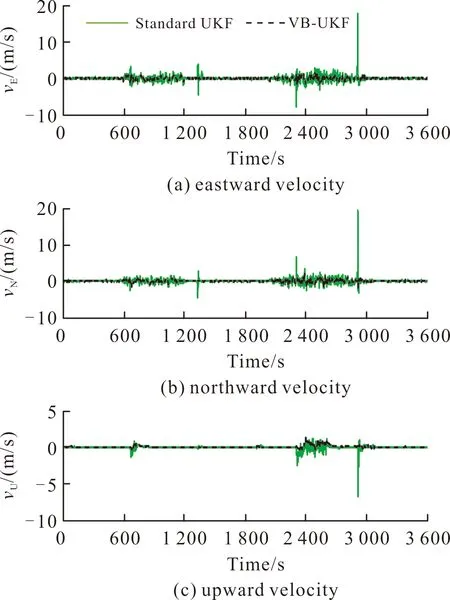
圖8 速度誤差曲線對比圖Fig.8 Velocity error curve comparison

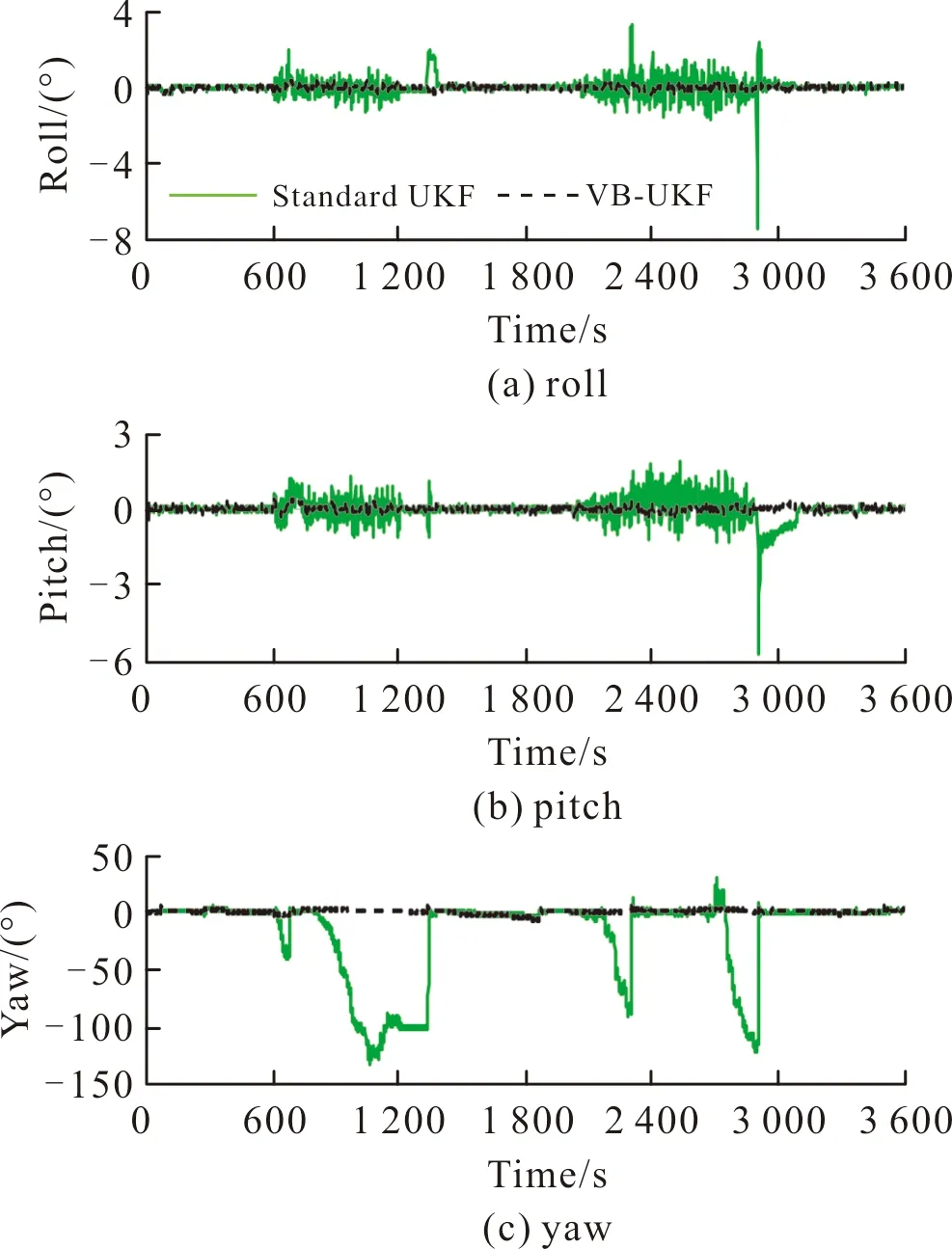
圖9 姿態誤差曲線對比圖Fig.9 Attitude error curve comparison

當前述的迭代步數j≥3時,量測噪聲均方差的估計精度變化可忽略不計,且也不會對組合導航系統的濾波精度形成影響。

為了定量分析圖7～圖9所示的兩種濾波算法的濾波精度,在整個導航時段內,表2給出了基于VB-AUKF算法及標準UKF算法的各導航參數誤差均方差統計分析。

表2 基于VB-AUKF及標準UKF的導航參數誤差統計分析Table 2 Statistical analysis of navigation parameter error based on VB-AUKF and Standard UKF

由表2可以看出,相對于標準UKF算法,VB-AUKF算法可提高位置精度及速度精度分別約12%及51%;提高橫滾角及俯仰角精度約75%,同時可以改變航向角在量測噪聲均方差變化時存在的發散現象。為此,基于VB-AUKF算法可以克服標準UKF算法不能自適應調節量測噪聲均方差的缺陷,進而提高了濾波器的魯棒性。

4 結論

基于GNSS/SINS組合導航系統的非線性濾波模型的特點,為了聯合估計系統狀態參數及量測噪聲統計特性,提出了組合導航系統的VB-AUKF算法,并建立了量測噪聲方差的迭代估計模型;針對決定量測噪聲均方差估計精度的3個參數、組合導航系統的VB-AUKF算法性能,論文進行了仿真實驗。

仿真結果表明:量測噪聲均方差估計模型的調節因子是決定均方差估計精度的關鍵因素,而其他2個因子的選擇僅僅影響均方差估計的初始值;相對于標準UKF,當量測噪聲均方差發生變化時,VB-AUKF算法可明顯提高組合導航系統的濾波精度。